黑赤松生长与年降水量关系研究

巩延苹(山东省林业监测规划院，山东 济南 250014)

黑赤松生长与年降水量关系研究

巩延苹
(山东省林业监测规划院，山东 济南 250014)

通过对黑赤松(Pinusthunbergii×P.densiflora)解析木材料的研究，得出该树种树木生长的拟合经验方程，即以年生长量为变量、以年降水量为自变量的函数，通过对函数的求导等数学运算，求出树木生长的年降水阈值，结果显示：黑赤松的现实林的生长速度最快的年降水量为532.7 mm左右，年降水量低于137.4 mm和高于1 065.4 mm出现负增长。

黑赤松；年降水量；年生长量；数学模型

在各种种植业生产实践中，经常会被旱涝的问题困惑，也就是说由于降雨量的时空分布不均，而对生产造成不良影响，在林业生产中更是如此，有许多人利用年轮资料与年降雨量资料的分析，得出年降雨量的变化对树木生长无显著性影响的结论，笔者认为他们得出的结论可能出于个例，有可能数据观测不准(如假年轮的影响等)，也有可能年降雨量不是树木生长实地的资料所致，更有可能是其他因素综合影响的结果。笔者借助解析木数据资料，以黑赤松(Pinusthunbergii×P.densiflora)为例对其与年降雨量的关系问题进行研究。

1 资料来源

历年降水量资料由烟台市牟平区气象局提供，解析木材料来自2009年12月中旬笔者采自烟台市牟平区大窑镇一棵53年生长正常的黑赤松解析木。胸径段用2.6 m区段，别的采用2 m区段，分别在树高5 cm(0盘)、1.3 m、3.6 m、5.6 m、7.6 m、9.6 m、10.6 m处截取圆盘，严格按照解析木的技术要领进行判读，以5年为龄级收集有关资料(过程从略)。

2 研究方法

为了节约研究成本，笔者借助树木生长经验方程，根据东北林业大学1985年编《测树学》教材，对各种回归方程进行拟合试验，最后决定采用以下混合型经验方程：y(p)=ea-b/p(a,b分别为待求函数的指数参数，e为自然对数的底数2.718 28……)，对树木生长过程进行研究，由于树木生长受各种因素影响，但对黑赤松影响最大的是降水量大小及时空分布均匀与否，笔者试图用经验方程拟合树木生长过程，通过对胸径拟合方程(包括求导生成方程，在研究过程中进行表述)的最大累计年降水量的取得，得出影响胸径等测树因子生长的降水量各种指标。用y(p)=a-b/p，y(p)=a+bp，y(p)=a+blnp，y(p)=1/(a-blnp)，y(p)=1/(a-bp)，计算限制树木生长的年降水量阈值及限值。

3 研究过程

通过对5年内树木生长过程方程拟合检验分析，除7.6米径(用符号D7.6表示，余者相同)和其平方(用符号D7.62表示，余者相同)及材积外的测树因子，也存在方程拟合关系，但是经检验可靠度较低，均在90%以下，于是笔者仅对表现显著的这3个测树因子进行分析研究。对各种拟合方程，通过各种数学运算，形成一元线性方程(是一元线性方程的直接应用)，然后用一元线性回归的办法，求得参数a，b值，并进行F检验和相关系数(R)检验，通过检验，即建立树木生长拟合方程，计算结果见表1，通过查表均以90%以上的可靠性通过检验，说明这些数学模型(即经验拟合方程)从整体上是适用的。下面以7.6径项目为例进行说明拟合方程求树木的连年生长量最大时间和数量成熟问题。树木胸径生长降水量拟合混合型方程y(p)=ea-b/p(随降水量变化的生长量，对表中Y(p)函数求导完成，从略，只给出极值点，下同)的极值点pz=1 203 mm，即树木在5年内累计降水量达到1 203 mm时，当年水资源贡献生长量达到最高峰(即水的即时利用效率最高)，而且是单一峰值，树木平均生长平均水资源利用效率方程Y(p)/p(年平均单位生长量所耗水资源折合降水量，从略，只给出极值点，下同)的极值点pm=2 406.1 mm，即降水量5 年内累计达到2 406.1 mm(年均481.2 mm)时，即年均水资源利用效率最高(以上只表述了D7.6拟定方程，D7.62拟定方程也是一样，笔者不再重述，在下面的论述中，生长拟合方程、pz、pm等各符号含义也相同，笔者不再赘述和解释，直接给出计算结果)。各项目求出的降水量累计要求和各种阈值,如表1所示。从表1中看出方程y(p)=ea-b/p中的D7.62与D7.6相比各参数值提高一倍，精度与检验F值，R值相等，这是由指数数学关系造成的，为了与蓄积进行比较，笔者特意把D7.62也当作测树因子对待建立拟合方程，其他拟合方程除对数倒数方程指数相近，D7.62方程拟合精度低于D7.6外,其余则是D7.62的拟合方程指数则是胸径的数倍,拟合方程的精度胸径表现得较高,而D7.62拟合方程得出和各种阈值具有十分惊人的相似性，而D7.62拟合方程相差就较大，因此利用D7.62(及其他树径如地径，3.6 m树径的平方等)及材积进行方程拟合，不失为一个研究的好途径，使试验结果更为稳妥。从表中我们还可以看出，D7.62对数倒数拟合方程得出的阈值9984mm与胸径指数拟合方程y(p)=ea-b/p得出的累计水资源利用效率最高值5 208 mm(也是D7.62拟合水资源累计利用效率即时最高值)相差近一倍，相对差距有91.7%。

为了列表方便，笔者用符号表示，例如1 101.2 mm(±5 a)意思是5年内累计达到1 101.2 mm有效降水量时，树木由负增长变为正增长，把这一值称为限值；符号4 113.1 mm(±∞5 a)的意思是在5年内有效累计降水量达到4 113.1 mm时，出现理论上的无限制增长也是达到最大生长量，但是一旦超过这一数值，就出现无节制地毁灭性负增长，因此把这一数值又叫阈值(下同，不再赘述)。

表1 5年内树木生长过程经验方程拟合表

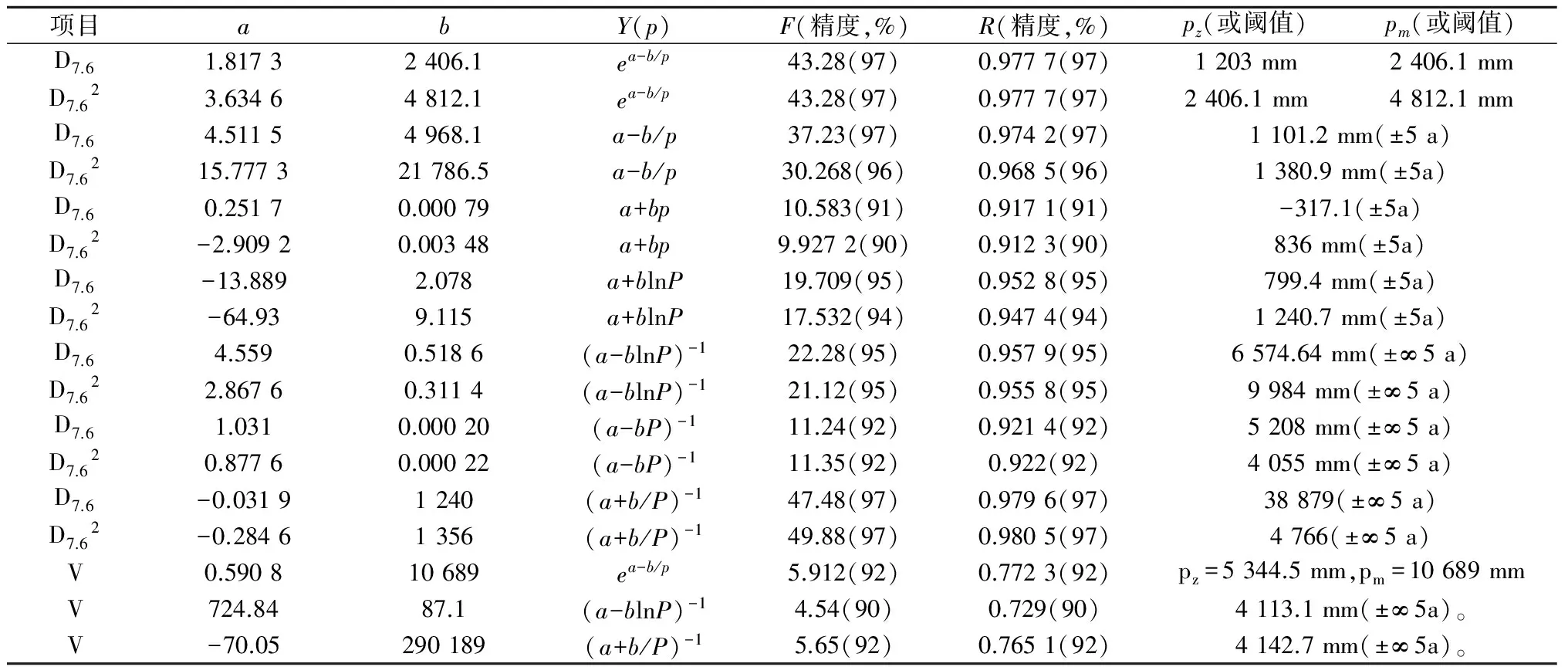
项目abY(p)F(精度，%)R(精度，%)pz(或阈值)pm(或阈值)D7．61．81732406．1ea-b/p43．28(97)0．9777(97)1203mm2406．1mmD7．623．63464812．1ea-b/p43．28(97)0．9777(97)2406．1mm4812．1mmD7．64．51154968．1a-b/p37．23(97)0．9742(97)1101．2mm(±5a)D7．6215．777321786．5a-b/p30．268(96)0．9685(96)1380．9mm(±5a)D7．60．25170．00079a+bp10．583(91)0．9171(91)-317．1(±5a)D7．62-2．90920．00348a+bp9．9272(90)0．9123(90)836mm(±5a)D7．6-13．8892．078a+blnP19．709(95)0．9528(95)799．4mm(±5a)D7．62-64．939．115a+blnP17．532(94)0．9474(94)1240．7mm(±5a)D7．64．5590．5186(a-blnP)-122．28(95)0．9579(95)6574．64mm(±∞5a)D7．622．86760．3114(a-blnP)-121．12(95)0．9558(95)9984mm(±∞5a)D7．61．0310．00020(a-bP)-111．24(92)0．9214(92)5208mm(±∞5a)D7．620．87760．00022(a-bP)-111．35(92)0．922(92)4055mm(±∞5a)D7．6-0．03191240(a+b/P)-147．48(97)0．9796(97)38879(±∞5a)D7．62-0．28461356(a+b/P)-149．88(97)0．9805(97)4766(±∞5a)V0．590810689ea-b/p5．912(92)0．7723(92)pz=5344．5mm，pm=10689mmV724．8487．1(a-blnP)-14．54(90)0．729(90)4113．1mm(±∞5a)。V-70．05290189(a+b/P)-15．65(92)0．7651(92)4142．7mm(±∞5a)。

从表1可以看出，V的两个阈值非常接近，相对误差限只有0.7%，均到每年为882.5 mm，很有现实指导意义，即浇水当量不能超过这一数值。其中D7.6阈值38 879(±∞5 a)没有实际意义，可能是由于数学方程和局限性或者是样本数量太少的原因造成的，因此选用多个数学方程进行比较对照，选择较多的样本单元是何等的重要。

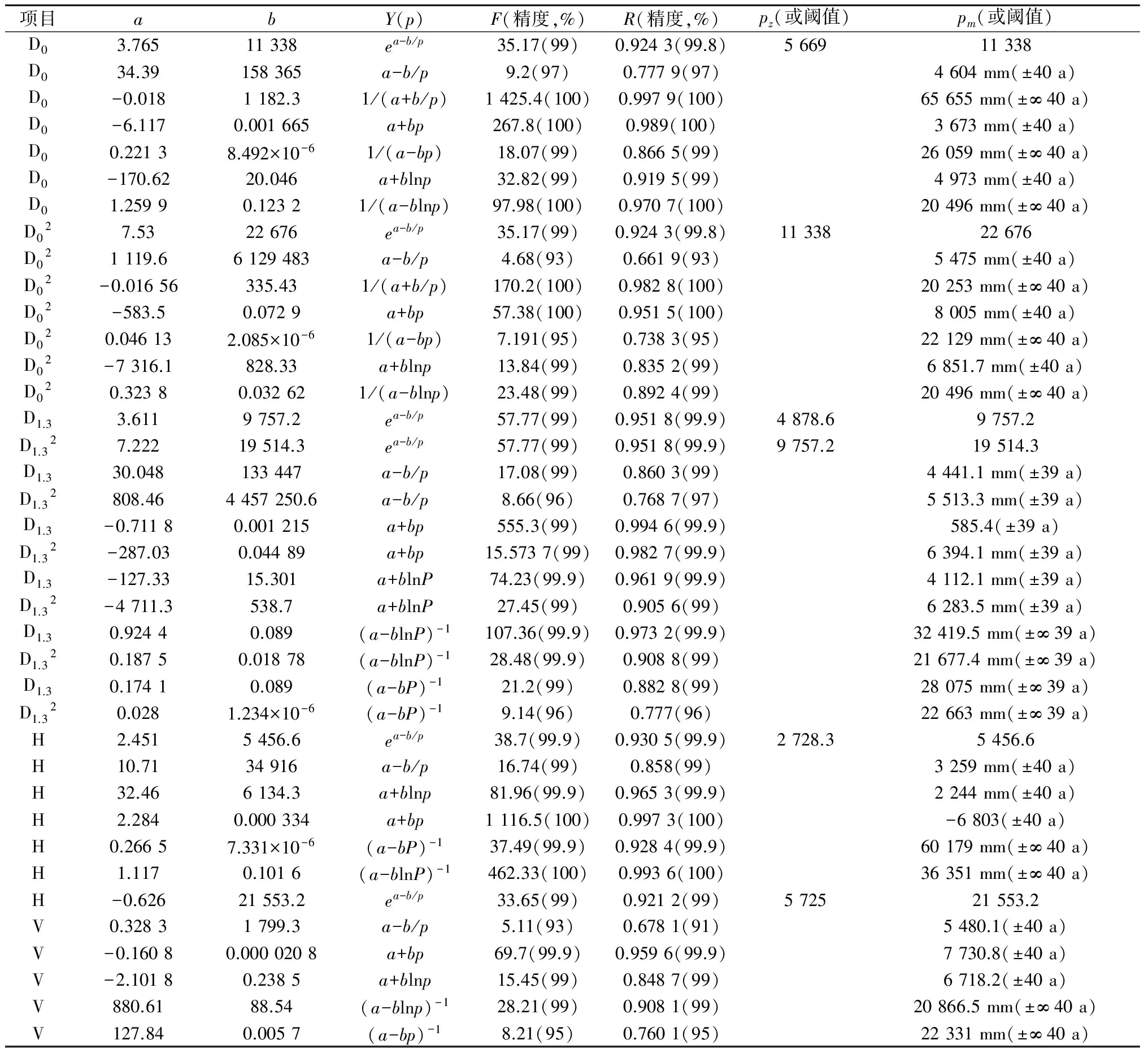
表2 40年内树木主要测树因子生长过程经验方程拟合表

表3 40年内树木生长次要测树因子过程经验方程拟合表

通过对40年内树木主要测树因子生长过程方程拟合检验分析，所有测树因子均存在方程拟合关系，可靠度及相关系数较高，精度大部分在99%左右，几乎接近100%，各种方程关系及数值列表2(表中分别用D0、D1.3、H、V分别代表地径、胸径、树高和材积，下同)，数值含义同5年内胸径拟合方程的表述，笔者不再赘述。其中H的限值-680 3(±40 a)没有实际意义，可能是由于数学模型的局限性造成的，但是它的相反数与同一数学模型D1.32的限值6 394.1 mm(±39 a)极为相近，是否可以用其相反数，需要下一步更多的试验加一验证。从表中也可能看出V的两个阈值相对其他测树因子来说比较接近，相对误差限只有7%，这与表1的表现基本吻合。表2中的拟合精度有的是100%，并不是完全达到了100%，而是无恨接近了100%，我们知道相关系数达到1时才是100%，但是受到主客观噪声的影响，很难达到(下同)，拟合精度之高说明材料的准确性和所选拟定方程的适用性，因此试验结果具有较高的科学价值。

笔者把其他测树因子，经方程拟合，精度通过检验的，也列出了表3(分别用符号D3.6、D5.6、D7.6代表3.6 m径、5.6 m径、7.6 m径)，大部分以99%～100%的可靠性通过检验，表中数字含义同表1与表2。表3中的D5.6阈值-201 477 mm(±∞28 a)与在7.6限值-106.3(±17a)因为是负值，没有实际意义，从另一侧面说明黑赤松具有较强的耐旱性。但是D5.6阈值-201 477 mm(±∞28 a)的相反数由于数量过大，也同样没有实际意义，但与表1没有实际意义的D7.6阈值38 879(±∞5 a)较为接近，年均相对误差限为9.3%。D7.6阈值119 281 mm(±∞17 a)由于数量过大也无实际意义，但它与没有实际意义的D5.6阈值-201 477 mm(±∞28a)的相反数更为接近，年均相对误差限只有2.6%，从中也说明了此研究的局限性。但是这些阈值或限值，是多年(5年以上的)，其绝对值除以5；是5年的，除以它的测树因子的实际年龄(例如D7.6为17 a)，与其他方程得出的限值和阈值比较接近。所有因子的平方及材积均没有出现没有实际意义的阈值和限值，其原因需要我们的林学家及数学家的进一步探究。从中也可以看出在生产实践中，要选择更加可靠的评价因子，以免造成不必要的失误。从表中也可以看出，因子的平方得出的限值及其阈值更有实践的指导意义。

4 结论与应用

通过研究结果的分析判断，各种测树因子与降水量的多少及其分布的均匀与否均有十分明显的相关关系。树木材积生长，在降水量时空分布均匀的条件下，当5年内累计降水量达到5 344.5 mm时，年生长量达到最大值，即时水利用效率最高；当累计降水量达到10 689 mm时，年平均单位水资源贡献生长量达到最大值，平均水利用效率最高；40年内当年降水量低于193.3 mm时，树木出现负增长，甚至出现死亡现象；当年均降水量达到822.6 mm时,出现理论上的材积无限增长量,但一旦超过这一阈值,将会出现毁灭性负增长现象,即树木因涝死亡(胸径的这一阈值为831.3 mm，胸径平方为555.6 mm)。当5年内年均降水量达到1 068.9 mm时，水资源即时利用效率最高；当年均降水量达到2 137.8 mm时，年均水资源利用效率最高。根据以上研究结果笔者建议，当预报年降水量不足555.6 mm，可适当浇水，以喷灌滴灌为主，浇水最大量不要累计超过822.6 mm(含自然降水量)，千万不要好大喜功，理论上的无限增长量，现实中是很难达到的理想状态，即使有也是极不稳定的一种状态，这就是物极必反的道理。

5 讨论

笔者用模拟方程对树木生长量与降水量关系进行研究，开辟了一种崭新的途径。先前许多学者可能是由于测量不准确不专业，收集数据较少的原因，而得出树木生长与降水量相关关系不明显的结论，只有做大量艰苦细致的工作，方能得出正确的结论。笔者在研究中发现，量纲的选择不影响试验结果，各种线性及类线性(经过对数、指数等的化简可转化线性方程的)方程，其试验结果与精度有一定差别，但能各自说明不同的问题，试验精度差别不大，长期的数值拟合方程比短期拟合方程试验精度更高，更能说明问题，因此选用时间长的样本值是何等的重要。本研究是由于树木样本采集的困难及笔者经费有限,借助解析木材料,利用树木生长拟合经验方程，也回避了由于各种自然条件时空上差异及树木分化现象对试验结果的噪声影响，得出各种试验结果。 但这毕竟是由单株树木的研究得出的结论，需要在以后研究和实践中反复验证，并请有关专家鉴定后方可付诸应用。但是要搞这项研究如果从处理对照的角度，则会更为精确，那要投入大量的人力物力，并得最少几十年甚至上百年的试验周期才能达到，笔者这一研究方法不失为一种简洁便捷可靠的办法，可在以后的科研与生产实践中推而广之。

[1] 东北林业大学.测树学[M].哈尔滨：东北林业大学出版社，1985

[2] 东北林业大学.数理统计学[M].哈尔滨：东北林业大学出版社，1985

[3] 刘国杰.注册咨询工程师(投资)执业资格考试教材复习指导[M].天津：天津大学出版社，2003

Relationship Between Growth and Annual Precipitation ofPinusthunbergii×P.densiflora

Gong Yanping
(Shandong Forestry Monitoring and Planning Institute, Jinan 250014, China)

Based on the study ofPinusthunbergii×P.densiflora, the fitted empirical equations of tree growth was obtained,that is ,the function of taking annual growth as variation and taking annual precipitation as independent variable,through mathematics operation of derivation, precipitation threshold of growth for trees were found .Result shows that the maximum annual rainfall rate of the reality forest is about 532.7 mm, the annual precipitation is less than 137.4 mm and higher than 1 065.4 mm,showing negative growth.

Pinusthunbergii×P.densiflora; annual precipitation; annual growth; mathematical model

1005-5215(2017)06-0041-04

2017-04-21

巩延苹(1975-),女，山东无棣人，大学，高级工程师，从事数字林业研究.

S162.5

A

10.13601/j.issn.1005-5215.2017.06.016