第二类 Volterra 积分方程符号计算设计
2017-07-03凌宗虎
凌宗虎
(安徽师范大学 数理统计学院,安徽 芜湖 241000)
第二类 Volterra 积分方程符号计算设计
凌宗虎
(安徽师范大学 数理统计学院,安徽 芜湖 241000)
在设计的基于微积分运算的符号计算系统中,对于连续核、L2-核的第二类 Volterra 积分方程,设计并实现了计算迭核的方法,通过求其解核得到该积分方程的解析解,为机械求解弱奇性积分方程提供了求解方法。
积分方程;解核;符号计算
1 研究背景
符号计算和数值计算是两种不同的解决科学和技术发展中问题的计算方法。数值计算方法可以求解部 分积分方 程 (组 )的解析解[1-4]。 符 号 计 算方法 只能得到大部分问题的近似局部解或近似解,而且计算量 大且表 达 形式庞 大[5]。
对于积分方程的符号计算问题,部分符号计算软件通过规定格式的某种方式的参数输入,可以得到部分积分方程的解析解,如目前有代表性的通用符号计算软件 Maxima、MATLAB、MAPLE、Mathematica 等。 部分积分方程可以使用 Laplace 变换予以求解[6-8]。
针对积分方程的符号计算求解难题,设计了以自然语言为输入方式的、建立在基本积分和微分基础之上的符号计算系统。 对于一类连续核和 L2-核的第二类 Volterra 积分方程, 设计实现了一种高效算法,可以以自然语言形式计算输出该类别积分方程的解析解。
2 待求解问题的描述
第二种 Volterra 积分方程定义为[9,10]
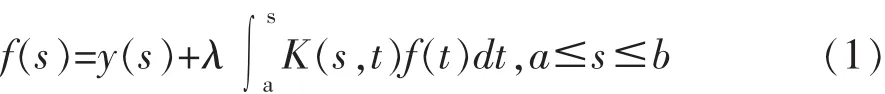
其中 y(s)∈L2[a,b]是一个给定的函数,K(s,t)是正方形△:a≤s,t≤b 上之一连续核或者 L2-核, 且当a≤s<t≤b 时为零,称为 Volterra 核函数。 例如:

级数
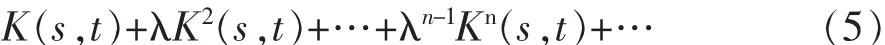
对 任 一 复 数 λ 都 几 乎 一 致 绝 对 收 敛[10]。 该 级 数的和函数 Hλ(s,t)称为核函数 K(s,t)的解核。
对于任意的连续函数或者 L2-函数 y(s)和任意λ 值,方程(1)有唯一的连续解或者 L2-解:

符号计算求解过程中的难点体现在以下两点。
1. 当 Volterra 核 函数具 有 某种特 殊 性质时 ,使用符号计算方法计算其各次迭核 Kn(s,t)和解核 Hλ(s,t)。
2.含参积分的符号计算,含参积分的偏微分计算,以及求解过程中积分参数的确定方法。
3 符号计算算法描述
这类积分方程的符号计算算法如下:
1.从自然语言中解析核函数以及各个变量表达式,组成一个待解集合:
{K(s,t),y(s),{x,s,λ,a}}
2.应用含参积分的计算模块,计算一次迭核,得到以下迭核序列:
其中 n≥2,i=1,2,…,n-1
3.应用级数和函数计算模块,判断所得到序列构成的级数(5)的和函数可解性,如果可以级数和函数则转下一步,否则转第 2步。
4.应用解核 Hλ(s,t)和 y(s),计 算原积 分方程 的解析解。
特别地,如果核函数有如下形式:
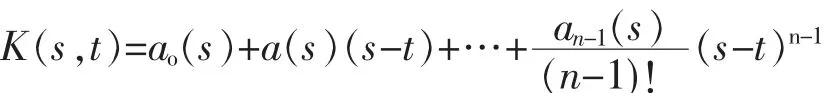
其中 ,ai(s),i=0,1,…,n-1 在[a,b]中连续。 则 解核函数计算结果如下:

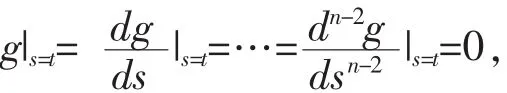
求解算法中需要应用线性偏微分方程的计算模块,以及应用线性方程组求解积分参数的模块。
4 符号计算实例
以方程(3)为例,在本符号计算系统中,输入命令为 “解方程 f (s)=e^s*sins+2*s (0,s,(2+coss)/(2+ cost)*f(t)dt)”,显示自然表达式计算过程如下。

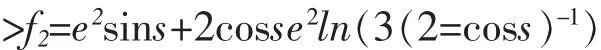
5 应用积分变换优化算法
对于下列类型的第二类 Volterra 积分方程
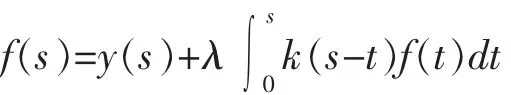
如果 K(x)是指数阶函数,则可以应用 Laplace 变换[11]简化求解过程。具体算法如下:
1.原方程左右两边求 Laplace 变换。
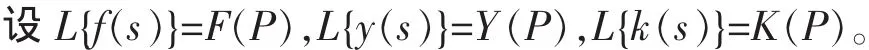
2.利用乘法定理得到 F(P)=Y(P)+K(P)*F(P),当 K(P)≠1 时 F(P)=Y(P)/(1-K(P))。
3.利用 Laplace 反变换,得到原方程的解。
以方程(2)为例,在本符号计算系统中,输入命令为“解方程 f(s)=sins+2*s(0,s,cos(s-t)*f(t)dt)”,应用 Laplace 变换求解方程(2),显示自然表达式计算过程如下。
>Laplace 变换:
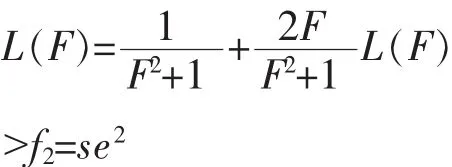
6 计算结果分析与比较
由于含参积分以及级数敛散性判断等解题步骤计算量大小不一,导致各个方程的计算量和计算时长有所差别。 以方程(2)、(3)和(4)为例,在同一台计算机上运行的结果如表1所示。
结果表明:
1.含参变限积分是符号计算积分方程的主要运算,包含各种积分方法。
2.特殊形式的核函数有比较特殊的计算方法,可以简化符号计算的过程。

表1 不同积分方程求解过程的比较
7 结束语
在第二类 Volterra 积分方程中,可以符号计算连续核函数或者 L2-核函数的解核,从而积分计算其解析解。对于特殊类型的核函数,符号计算过程可以优化,加快积分计算过程。
[1]阎 玉 斌,崔 明 根.第 二 类 Volterra 积 分 方 程 的 准 确 解[J].高 等学校计算数学学报,1993(04):291-296.
[2]张艳敏.Volterra 积分 方 程 组 的 精 确 解[D].哈 尔 滨 :哈尔滨工业大学,2006.
[3]夏 莉.Volterra 积 分 方 程 数 值 解 法 综 述[D].长 春 :吉 林 大 学 ,2009.
[4]刘唐伟,应正卫,吴志强.第二类非线性 Fredholm 型 积分方 程数值解[J].东华理工学院学报,2005(3):294-296.
[5] 互 动 百 科 . 符 号 计 算 [EB/OL].http://www.baike.com/wiki/% E7%AC%A6%E5%8F%B7%E8%AE%A1%E7%AE% 97,2012-09-28/2016-12-20.
[6]张 忠 诚.拉 普 拉 斯 变 换 的 应 用 研 究 [J].周 口 师 范 学 院 学 报 ,2006(2):40-42.
[7]施 晓 红.Laplace 变换在求解线性微分及积分方 程 中 的 应 用[J].昆明理工大学学报:理工版,2009(3):121-124.
[8]黎丽梅.拉普拉斯变换的数值逆在线性偏积分微 分方程中的应用[J].湖南理工学院学报:自然科学版,2006(1):8-11.
[9]张石生.积分方程[M].重庆:重庆出版社,1988:45-52.
[10]沈 以 淡.积 分 方 程 (第 二 版 )[M].北 京 :北 京 理 工 大 学 出 版社,2002:81-85.
[11]华中科技大 学 数 学 系.复 变 函 数 与 积 分 变 换 (第 三 版 )[M].北京:高等教育出版社,2008:227-235.
责任编辑:胡德明
Symbolic Computation Design for the Second Kind of Volterra Integral Equations
Ling Zonghu
(School of Mathematical Statistics,Anhui Normal University,Wuhu 241000,China)
In the designed symbolic computation system based on mechanical calculus,the computing method for iterated kernel in the second kind of Volterra integral equations for continuous and L2-cores is designed and realized.The analytical solution of the integral equation is obtained by solving the equation. It provides a method to solve the weak singular integral equation.
integral equations;kernel function;symbolic computation
O245
:A
:1672-447X(2017)03-0004-03
2017-02-21
凌宗虎(1969-),安徽芜湖人,硕士,安徽师范大学讲师,研究方向为数据库与网络软件、高性能计算技术。
