零区域作用下财富不平等形成机制研究

路 兰，高齐圣，刘瑞超

(青岛大学 经济学院，山东 青岛 266071)



零区域作用下财富不平等形成机制研究

路 兰，高齐圣，刘瑞超

(青岛大学 经济学院，山东 青岛 266071)

财富和收入不平等的演进一直备受关注，为了更好地理解社会经济系统中财富不平等形成机制，基于社会资本理论构建了零区域(zero range process, ZRP)作用下的财富网络演化模型。通过理论推导给出了财富发生凝聚时财富转移速率的临界值，该结论与微观模拟结果是一致的。其次，财富转移速率指数与个体社会关系强度指数具有明显的线性关系，关系强度越大则财富转移速率越快，从而社会财富就越容易发生凝聚。最后，结合相关结论给出了政策建议。

零区域作用；微观模拟；财富转移；财富凝聚

一、引言

在现代经济发展进程中，财富和收入不平等的研究一直备受关注。自库兹涅茨“倒U”型假说提出以来，集中到均化的财富分布演变过程一直是学术界对不平等与经济增长关系的最理想解释。但是现实中，该假说的成立性越来越受到怀疑。根据瑞信提供的2010—2016年度《全球财富报告》的相关数据，由图1可知，财富分布顶层的人口所支配的全球财富值从2010年的35.5%增长到2016年的45.6%，而人口占比却由0.9%降低到0.7%，因此可以说全球财富不平等的程度逐年扩大。在不断高涨的财富不平等压力面前，没有人能明确说出财富不平等的形成机制是什么，财富不平等背后的推动力量又是什么？

图1 2010—2016超高净资产人群财富占有比

Spitzer(2000)[1]是最早在ZRP的框架下研究凝聚现象的，之后一些研究揭示了凝聚是由于粒子之间的吸引或者混乱的破坏引起的[2]。在现实社会中也存在着类似的现象，例如管道阻塞、城市的形成以及生物系统中个体区域集聚成群等等。在经济系统中，个体所拥有的财富值不断地被转移和重新分配，在经过无数次的转移和传递后，最终都汇聚于极少数人的手中，形成一种“赢者通吃”的现象。这个过程跟复杂网络的凝聚过程极为相似，由此我们说社会中的财富演化同样也存在着凝聚现象。这种凝聚类似于凝胶过程，拥有最大财富值的个体作为“胶核”，它将其他的个体胶结在自己周围。其次，林南的社会资本理论认为[3-4]，社会结构是由人的网络构成的，这些人的位置按照控制和摄取有价值的资源的能力呈金字塔状排列。个体社会网络的异质性、网络成员的社会地位、个体与网络成员的关系强度决定着个体所拥有的社会资源的数量和质量。占据或接近社会结构金字塔顶端的网络成员，控制和摄取个人财富的能力较强，这不仅由于更多的有价值资源内在地附着于这些位置，而且因为处在这些位置具有接近其他等级位置的最大可能性。所以说社会关系网络也是造成财富不平等的一个重要方面。

因此，本文基于社会资本理论，利用复杂网络凝聚的思想，通过模拟微观个体所拥有财富值的流动过程，反映出个体真实的财富积累行为，从而找到财富凝聚的临界点，并对产生凝聚后的财富稳态分布形式与之前研究的结论进行对比，从而给出社会财富不平等形成机制的理论分析。

二、文献综述

国内从个体财富积累动机和行为解释财富分布的文章并不多，王弟海、龚六堂(2006)[5]讨论了当个人劳动能力和偏好存在差异的情况下，资本收入和劳动收入分配的差异如何通过遗产机制影响收入和财富分配的持续性不平等程度。王弟海、龚六堂(2007)[6]在外生技术进步和内生经济增长的经济中，讨论了持续性不平等的动态演化、稳定状态下持续性不平等的决定以及初始财富对持续不平等的影响。陈彦斌和邱哲圣(2011)[7]以中国房地产市场为背景，构建了包含内生性住房需求和生命周期特征的Bewley模型，用于刻画房价对居民储蓄行为和财产不平等的影响。陈峰、姚潇颖和李鲲鹏(2013)利用中国1999—2010年31个省市自治区中高收入家庭的93个收入分层截面面板数据，分析了住房市场独立决策的中等及以上收入家庭的住房财富效应及其结构性差异。

国外关于财富不平等形成机制的研究主要从财富积累动机这个角度开展，提出了许多有关个体间财富交换的模型。Dragulescu和Yakovenko(2000)[8]提出了一个DY模型，该模型认为用于交换的财富是社会总财富的一部分。随着时间的不断演化，模型中的财富分布趋近于Gibbs分布，这个分布是稳定的，与交换空间的拓扑结构是无关的。这个模型比较简单，忽略了个体财富积累的动机，比如说生命周期、风险预防、贪婪等等。Chakraborti(2000)[9]提出了一种带有存储率的财富交易模型，即CC模型。但该模型中所有个体的存储率都是相同的，与实际情况不相符。随后，A.Chatterjee(2004)[10]等人又提出了CCM模型，该模型中个体的存储率是存在异质性的。Asim Ghosh和A.Chatterjee(2016)[11]等人对模型CC及CCM进行了财富分布的对比分析，并针对不同国家计算了不平等指数、Gini系数等指标值。Iglesiashe Goncalves(2004)[12]提出了一种带有风险意识的财富交易模型，模型中通过概率p将财富进行了重新分配，从而降低了贫穷者与富有者之间的财富差距。Ning Ding等(2005)[13]基于贪婪性提出了一种带有偏好性的财富交易模型，模型中假设个体每次交易都选择拥有较多财富的个体进行。Cagetti等(2003)将生命周期储蓄和预防性储蓄动机相结合[14]，对两种动机导致的财富不平等进行了比较，并指出在生命周期的开始阶段财富积累在很大程度上是被预防性储蓄动机诱导的，当个体接近退休，养老储蓄动机更加明显。Riado T. Fernholz(2016)[15]在宏观经济环境下，采用实证分析的方法讨论了不可保的投资风险条件下财富分布的特点，其结论与Benbabib等(2011,2016)[16-17]的结论类似。以上模型均是考虑了相互作用的经济个体的集合，不同个体间进行财富固定值交换或是财富随机交换，且均没有考虑社会资本关系结构。进而，MaoBin Hu等(2007)[18]首次在无标度网络的基础上模拟了个体间的财富交易，分析得出这种无标度关系结构是导致富者愈富的重要原因。Vazques Montejo(2010)[19]等首次将财富交易机制引入到网络结构中，进而根据财富交易机制进行财富的转移与演化。以上研究虽然考虑了社会关系结构，但并没有对社会资本理论在社会财富不平等形成过程中的影响机制进行分析；此外，还没有文献从财富凝聚的角度对社会财富不平等形成机制进行解释。

为了更好地理解社会财富不平等的形成机制，本文在社会资本理论的基础上构造了ZRP作用下的财富流动模型。通过平均场速率方程解析得到了财富值的相变点和稳定态分布情况，并根据实际的财富流动的特点引入了个体社会关系强度k以及个体诚信度η两个参数，最后通过仿真分析给出了不同参数下的财富粒子的稳定分布图以及各参数之间的关系图，与理论推导的结果是完全一致的。

三、社会资本在财富不平等形成中的机制分析

社会资本这一概念最先是由法国的社会学家皮埃尔·布迪厄在1980年提出来的，科尔曼和帕特南两位著名学者一起发展构成了社会资本的基本理论框架[20]。大部分学者认同帕特南对社会资本的定义，将其解释为“能够通过推动协调的行为来提高社会效率的网络、规范和信任”。社会资本的核心要素包括以下三个方面：(1)社会资本的社会网络；(2)成员认同的规范；(3)相互间的信任。目前我国社会中个人的社会资本结构以工具性的社会关系为主，即人与人之间后天形成的各种交往关系，包括地缘性和业缘性的关系。

本文研究的前提就是个体之间已具有一定的关系结构，而这些关系汇总起来成为一个无标度的社会网络，也就是说形成了社会资本意义下的网络、规范和信任。

首先，在财富流动方向上，有效地利用了个体之间形成的地缘性和业缘性关系。一般而言，财富粒子的流动往往更易发生在已有的相互关联的个体间。这里的个体可以看作是个人、企业或是国家，与传统银行信贷考察财务报表数据等“硬资料”不同，对合作伙伴的考察更加重视成员的个人性格、人品、信誉等“软指标”来控制信用风险，并且每个个体的社会关系强度也是不同的。其次，在财富流动准则上，虽然不同个体的初始禀赋不同，即个体所拥有的初始财富值以及个体的诚信度不同，但是文中我们假设所有个体间的交易都是根据相同的规则来进行的。这就满足了社会资本意义下的规范。最后，在财富流量的大小上，个体的诚信度越高以及个体的社会网络关系越强，则该个体获得财富粒子的概率就越高。这也是社会资本意义下对信任的体现。

所以说，基于社会资本的视角分析财富流动机制是可行的。财富是存量，存量的不平等是流量不平等长期累加的结果。财富不平等来源于财富积累过程中不平等财富流的多期累加。在不考虑制度改革因素的条件下，财富积累主要是内生性的积累。将财富不平等内生化的常用方法是微观模拟。微观模拟通过个体行为假设，反映个体真实的财富积累行为，通过参数校准再现实际的财富分布状况，给出微观经济体动态变化与财富分布之间的关系。

个体财富积累行为主要是由财富积累动机、财富积累能力以及财富积累方式3个方面决定的。财富积累动机决定了个体财富积累的时机和数量，在现实社会中，由于财富积累动机的存在，交易对象的选择是具有个性化偏好的，也有从众心理，但很少有人会随机地去选择交易对象。凯恩斯列出了风险预防、生命周期、跨期替代、改善、独立、投资活动、遗产、贪婪等八种积累动机。文中我们模拟了贪婪与风险预防两种动机。贪婪是指个体在进行财富转移时，会选择具有财富量较多的个体进行，由此提高自己获得更多财富的可能性。风险预防是指个体在考虑收益的同时，还会尽可能的降低自己的投资风险，即选择一个诚信较好的个体进行投资。财富积累能力不同的主要原因除了劳动禀赋差异外，在一个重要的原因就是代际传递所造成的初始财富不平等。因此文中对不同的个体分别赋予了不同的初始财富值ni以及不同的诚信度ηi。根据物以类聚人以群分的社会规律，个人的诚信度越高越容易吸引其他个体与其进行合作，即假定ηi=λikiα，其中λi为[0,1]之间的随机数，α可为任意值，ki表示个体的社会关系网络强度。最后关于财富积累方式，主要是指家庭之间在投资数量、投资组合和回报率上的差异。这里我们将所投资形式及结果均用量化的指标财富值来体现，财富的精确含义取决于具体的问题。例如，对于国际贸易中的所有国家，GNP或是一些宏观经济指标可以看做是有关财富的合理解释。

四、模型设定及理论分析

(一)ZRP作用下的财富网络演化模型

我们模型的前提是假设个体之间已具有一定的关系结构，由于关系强度的不均匀性以及个体信息的不对称性，这些关系汇总起来就成为一个BA无标度的社会网络。该网络结构的特点是节点度服从幂律分布，即少部分个体的关系强度很大，而大部分人的关系强度是比较小且较均匀的。此外，该网络的平均路径较短聚集系数较大，即整个网络的聚集性较好，任意两个节点间的联通路径较短，这与林南所提出的社会关系金字塔结构极为相似[4]。由此，网络中所有个体都遵循一定的原则，个体间的关系主要是业缘性关系，个体之间存在一定的信任，也就是说形成了社会资本意义下的网络、规范和信任。鉴于此，我们在传统的ZRP模型基础上，引入了社会关系强度及诚信度，提出了一个基于ZRP的财富网络演化模型，具体过程如下：

首先，假设N表示整个网络中的财富总值，L表示网络中个体总数。我们限定模型在N,L→的极限情况，财富密度为。每个个体i=1,…,L可能被任意数目的财富粒子所占据，且定义在每个节点i上所占财富粒子数是ni，表示个体i所拥有的财富值，其系统的微观态为n=(n1,n2,…,nL)。

其次，在动力学过程中，单位时间内每个财富粒子都以某一概率跳出所在的节点，粒子跳跃速率pi只取决于节点i上的粒子占有数ni。在粒子的运动过程中，粒子以一定的概率跳跃到相邻的位置上，概率只是取决于离开位置上的粒子数。换句话说，每个粒子相互影响是在同一个位置上的粒子，也就是零程相互作用(ZRP)。为了简单，我们假定每个财富粒子的跳跃速率都具有同样的函数。

pi=pi(n)=nδ

(1)

财富粒子的跳跃速率p(n)可以表示节点上粒子之间的相互作用。当p(n)∝n，粒子间没有相互作用，相当于粒子的随机行走；当p(n)增加的比n快时，说明财富粒子之间存在着排斥力；反之，说明粒子之间存在着吸引力。在本文中我们规定δ∈[0,1]。

第三，根据个人社会关系强度以及个人诚信度，我们设定跳出节点i的粒子转移到其邻居节点j的概率为

(2)

其中，ki表示的是个体的社会关系强度，ηi表示个体的诚信度，Bi表示节点i的邻居节点的集合。根据式(2)可知，社会关系强度ki以及节点的诚信度ηi共同决定了财富的转移方向。

最后，不断地进行个体间的财富转移与流动，直到系统中的财富分布达到稳定状态为止。

(二) 理论分析

运用平均场理论给出各节点上平均所占财富值的时间演化方程，通过这个方程来求解ZRP系统的相变点和稳定态分布。根据粒子跳跃(在每个时间步，以一定跳跃速率跳出所在节点i的粒子数)和汇聚过程(同时，该节点i可以接收到跳出其邻居节点的粒子数)，从而得到粒子系统的时间演化方程：

(3)

其中，mk(t)表示在t时刻联接度为k的个体平均占有的财富值，也就是所有度为k的个体所占财富的平均值；mkδ(t)表示此时财富的转移速率，即财富转移量；条件p(k′|k)指从度为k的节点发出的一条连接指向度为k′的节点的概率；k0与kmax分别是网络中最小和最大的度值。

当式(3)的右边等于零时，系统达到稳定态，从而我们可以得到处于稳态时个体的平均占有财富值mk，即得到

(4)

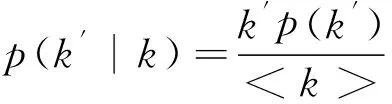
(5)

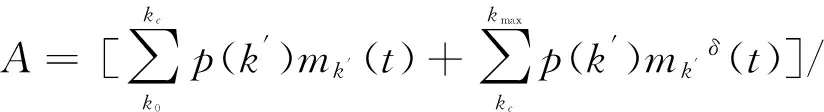
因而可得

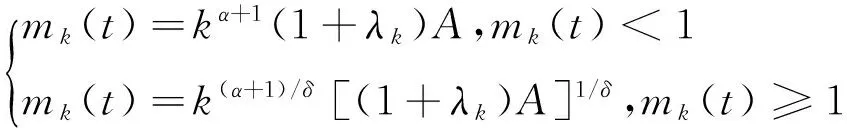
(6)

在mk=1时，k=kc，kc为节点度的临界值，由此可知

mk(t)=[(1+λk)A]1/δk(α+1)/δ

⟹1=[(1+λkc)A]1/δkc(α+1)/δ

⟹kc=[(1+λkc)A]-1/(α+1)

由此可得

(7)

所以

(8)

(9)

(10)

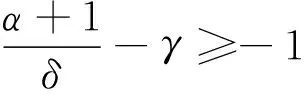
(11)

由此可知，当δ≤δc时，有聚集现象；当δ>δc时，无聚集现象。

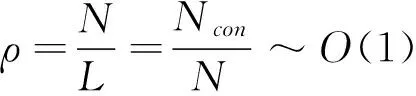
(12)

(13)

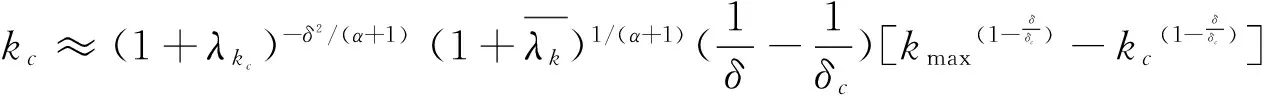
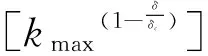
(14)

从上式中可以知道kc不依赖于粒子密度ρ，表明无论财富密度ρ为多大，经济系统均可发生财富聚集的现象。

五、微观模拟分析

从上述分析中可知，δc是财富发生凝聚的临界值，当δc<1时，p(ni)=niδc表示每个节点在单位时间内可以处理的粒子数；而当δc>1时，则在1≤δ≤δc的情况下，p(ni)=niδc均与δ=1的情况相同，即p(ni)=ni，即该节点上的所有粒子均跳跃到其邻居节点上，在必定会发生财富凝聚现象。因此以下从δc<1以及δc>1两种情形下进行仿真分析。仿真试验中令网络中节点总数N=2000，粒子数为L=1000。

(1)在α=0.2时，即δc<1

(2)在α=1.2时，即δc>1

图2 α=0.2时财富粒子的分布图

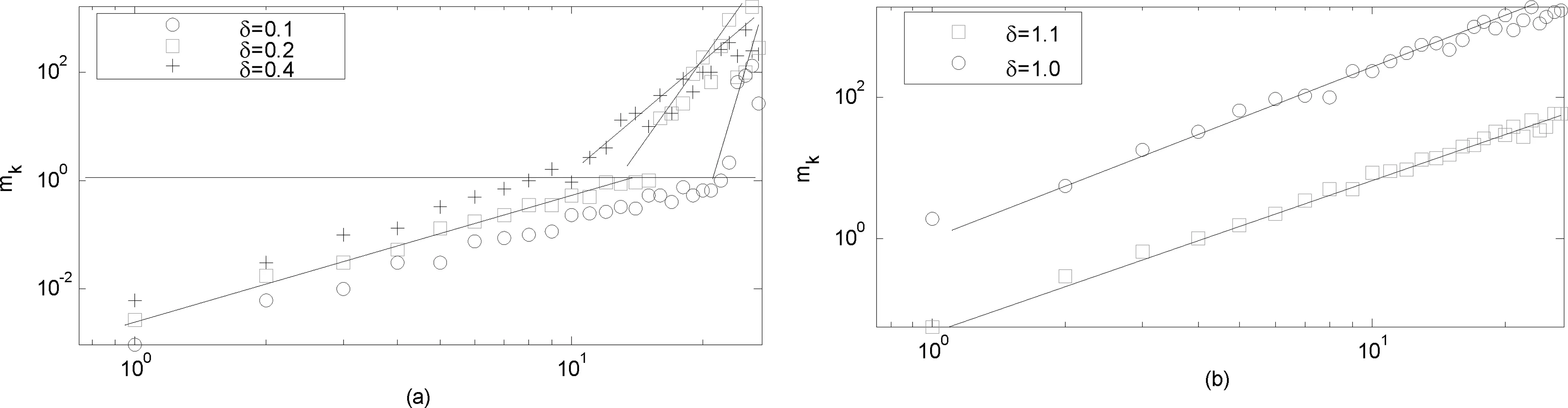
图3 α=1.2时财富粒子的分布图

(3)临界跳跃速率指数δc与指数α之间的关系

(4)δ与kc之间的关系图

图5中给出了δ与kc之间的关系图，从图中可以知道，无论α为何值，随着δ的逐渐增大，kc值逐渐下降，由此可知当δ达到一定值后，kc→0，系统将会发生凝聚，即财富粒子逐步转移到系统中的hub节点上。

图4 临界跳跃速率指数δc与指数α之间的关系

图5 δ与kc之间的关系

(5)节点度k与mk的关系图

图6中给出了节点度k与mk的关系图，图中分别给出了不同网络规模N下的度k与mk的关系曲线，其中α=0.2，δ=0.4。从图中可以看到，由于δ<δc，系统处于凝聚相，随着网络规模的不断增大，系统的凝聚现象仍然存在。在粒子数mk<1时，不同规模下的粒子分布曲线斜率是近似相同的，约为1.2；当粒子数mk≥1时，粒子分布曲线的斜率也是近似相同的，约为3。因此说系统始终存在财富的聚集现象。

图6 节点度k与mk的关系图

六、结论及政策建议

上述结论的政策含义在于：财富极化问题在经济视域中就是各类生产要素在某一时期不断地流向经济发达或发展快的区域或国家。生产要素流动速率越快，则发达或发展快的区域或国家的资本积累速度就越快，因此，政府需要不断加强落后地区的特色产业扶植，加强人才队伍建设，加强国家中心城市及区域中心城市的带动作用，从而形成一种良性循环，这样才会对落后区域和发展中国家的财富产生更大的吸引力。其次，从理论分析及模拟仿真发现，财富粒子跳跃速率与个体的连接强度有着明显的正比例关系，也就是说个体的社会关系强度越大，则该个体所拥有的财富的跳跃速率就越快。个体社会关系的强度是社会地位的表征，因此可以说社会地位分化显著地影响了财富凝聚速度。因此政府需要通过解决流动人口的户籍问题、流动儿童的医疗保障及上学问题，促进人口的不断流动，给社会各阶层的流动提供有效路径，从而带动社会财富在各个阶层间的流动，降低不平等程度。

[1]SPITZER F. A new class of models for surface relaxation with exact mean-field solutions[J]. Adv.Math, 1970,57(5):658-664.

[2] GODRECHE C. Dynamics of condensation in zero-range processes[J]. Journal of Physics A General Physics. 2003,36(23):6313-6328.

[3]LIN NAN. Social resources and instrumental action[M]. Beverly Hill,C.A：Sage, 1982: 131-145.

[4]LIN NAN. Building a network theory of social capital[J]. Connections, 1999,22(1):28-51.

[5]王弟海,龚六堂.持续性不平等的动态演化和经济增长[J].世界经济文汇, 2007(6):1-18.

[6]王弟海,龚六堂. 新古典模型中收入和财富分配持续不平等的动态演化[J]. 经济学(季刊), 2006(2):777-802.

[7]陈彦斌,邱哲圣. 高房价如何影响居民储蓄率和财产不平等[J]. 经济研究, 2011(10):25-38.

[8] DRAGULESCU A , YAKOVENKO V M. Statistical mechanics of money[J]. Eur. Phys. J. B .,2000,17(4):723-729.

[9] ARNAB CHATTERJEE. Kinetic models for wealth exchange on directed networks[J]. The European Physical Journal B, 2009,67(4):593-598.

[10] CHATTERJEE A, CHAKRABARTI B K, MANNA S S. Pareto law in a kinetic model of market with random saving propensity[J]. Physica A, 2004, 335(1):155-163.

[11] ASIM GHOSH, ARNAB CHATTERJEE, JUN-ICHI INOUE. Inequality measures in kinetic exchange models of wealth distributions[J]. Physica A, 2016, 451:465-474.

[12] IGLESIAS J R, GONCALVES S, ABRAMSON G, et al. Correlation between risk aversion and wealth distribution[J]. Physica A, 2004,342(1):186-192.

[13] NING DING，YOUGUI WANG，JUN XU, SING XI，Power-law diswibution in circulating money: Effect of preferential behavior[J]. International Journal of Modern Physics B, 2004,182-725．

[14] CAGETTI M. Wealth accumulation over the life cycle and precautionary savings[J]. Journal of Business & Economics Statistics, 2003,21(3):339-353.

[15] RICARDO T FERNHOLZ. A model of economic mobility and the distribution of wealth[J]. Journal of Macroeconomics, 2016, 50:168-192.

[16] BENHABIB J, BISIN A, ZHU S. The distribution of wealth and fiscal policy in economies with finitely lived agents[J]. Econometrica, 2011, 79 (1):123-157 .

[17] BENHABIB J, BISIN A, ZHU S. The distribution of wealth in the blanchard-yaari model[J]. Macroecon. Dyn. 2016,20 (2), 466-481.

[18] HU MAO-BIN, JIANG RUI, WU QING-SONG. et al. Simulating the wealth distribution with a richest-following strategy on scale-free network[J]. Physica A, 2007,381(15):467-472.

[19]VZQUEZ-MOMTEJO J, HUERTA-QUINTANILLA R, RODRIGUEZ-ACHACH M. Wealth condensation in a barabasi-albert network [J]. Physica A, 2010,389(7):1470.

[20]周红云. 社会资本及其在中国的研究与应用[J]. 经济社会体制比较, 2004(2):135-150.

[21] NOH J D, SHIM G M, HOYUNLEE. Complete condensation in a zero range process on scale-free networks [J]. Phys.Rev.Lett. 2005(94):198701.

(本文责编：辛 城)

Study of Fomation Mechanism of Wealth Inequality Based on Social Capital Theory

LU Lan, GAO Qi-sheng, LIU Rui-chao

(CollegeofEconomics,QingdaoUniversity,Qingdao266071,China)

The inequality in wealth and income has received much attention in China. In order to understand the formation mechanism of wealth inequality in social economical system well, a wealth flow model under zero range process is constructed based on the theory of social capital. By theoretical deduction, the critical value of wealth transfer rate is given which is consistent with the microscopic simulation result. Secondly, the linear relationship between wealth transfer rate index and intensity index of individual social relations is obviously. So, the phenomenon is that the greater the intensity of the relationship, the faster the rate of transfer of wealth. Thus, the social wealth is easier to become condensation. Finally, policies and suggestions are given based on the correlated results.

zero range process; microscopic simulation; wealth transfer; wealth condensation

2016-12-25

2017-04-09

山东省自然科学基金(ZR2016GP03)； 山东省高校人文社会科学计划项目(J16YE34)；山东省社科规划项目(16CJJJ43)

路 兰(1982—)，女，山东烟台人，青岛大学经济学院讲师，博士，研究方向：经济系统分析。

F222.33

A

1002-9753(2017)06-0184-09