基于能量聚集度经验小波变换的齿轮箱早期微弱故障诊断

王友仁 陈 伟 孙灿飞 孙 权 黄海安南京航空航天大学自动化学院，南京,211106



基于能量聚集度经验小波变换的齿轮箱早期微弱故障诊断

王友仁 陈 伟 孙灿飞 孙 权 黄海安
南京航空航天大学自动化学院，南京,211106

齿轮箱早期故障的故障特征不明显，振动信号呈现出强烈的非线性、非平稳现象，为此,提出了一种基于能量聚集度经验小波变换(EA-EWT)的齿轮箱故障诊断方法。首先对采集的振动信号进行EA-EWT分解，对分解后的各层信号采用最大峭度-包络谱熵准则进行敏感分量筛选，再利用最小熵解卷积对筛选出的分量信号进行降噪处理，对降噪后信号进行Hilbert包络谱分析，通过包络谱中的频率成分识别出故障类型，实现早期故障诊断。试验结果表明，该方法能够明显增强早期微弱故障特征，提高齿轮箱早期故障诊断性能。

经验小波变换；最大峭度-包络谱熵；齿轮箱；故障诊断

0 引言

齿轮箱是机械设备中必不可少的传动装置，广泛应用于航空、航天、农业、电力等领域。齿轮箱工作环境复杂，故障发生概率高、易损坏，因此准确实现齿轮箱早期微弱故障诊断，对避免经济损失具有重要意义。齿轮箱发生早期微弱故障时，由于故障不明显从而导致振动响应微弱，而齿轮箱内部存在多对齿轮啮合，故障齿轮和其余齿轮啮合会产生调幅和调频效应，故障齿轮会引起动态信号调制，增大了故障诊断的难度;另外由于负载变化会导致齿轮箱振动信号强烈的非线性、非平稳特性，种种原因叠加就加大了早期微弱故障诊断难度。

小波变换、经验模态分解(EMD)、集合经验模态分解、局部均值分解(LMD)等方法[1-4]，常被用于旋转机械故障诊断领域。小波变换虽改进了短时傅里叶变换的固定窗函数的缺陷，但对于不同的振动信号，其小波基函数选择不一致，缺乏自适应性；EMD能够将信号自适应分解为多分量，对所有分量做Hilbert变换能得到信号的时频分布，但EMD方法中存在模态混叠、欠包络、过包络、端点效应等问题；LMD方法虽然是一种良好的自适应时频分析方法，但该方法对噪声敏感，噪声成分使LMD分解层数增加，还可能导致算法不收敛等问题，致使原始故障特征信息提取困难。DAUBECHIES等[5]提出了同步压缩变换方法，在小波尺度域实现重分配，改善了小波变换时间-尺度域产生的频率模糊现象。DRAGOMIRESTKIY等[6]提出的变分模态分解也广泛应用于机械故障诊断领域，但该方法需要人为给定分解模态数量，当指定模态数量少时，则一个模态分量里面存在多个分量，无法正确区分；反之，当模态数量过多时，则计算量加大，且会出现较多模态分量接近的成分。GILLES等[7]结合EMD的自适应小波分析的框架，提出了一种新的自适应信号处理方法，即经验小波变换(empirical wavelet transform ,EWT)方法。该方法的优点在于能够构建合适的正交小波滤波器组，对信号的频谱进行划分，提取具有紧支撑的调幅调频成分，不存在模态混叠以及虚假分量等问题。该方法依据信号的频谱幅值进行频带划分，需要人为给定分解层数，文献[8-11]均对该方法做了一定的改进。当齿轮箱发生早期故障时故障特征微弱且易被干扰信号影响，信号呈现强烈的非线性非平稳性的多分量调幅调频特征，由于故障特征体现在复杂的边频带信息中，直接对振动信号进行EWT分解会出现较多模态分量接近的成分，且易丢失故障特征信号。

针对上述问题，本文引入能量聚集度概念，通过能量聚集度极值点的分布确定频带宽度与频带中心，提出了基于能量聚集度经验小波变换(energy aggregation and empirical wavelet transform, EA-EWT)和最小熵解卷积的齿轮箱故障诊断算法，并通过试验结果证明了该方法的有效性。

1 理论基础

1.1 经验小波变换(EWT)

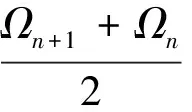
图1 经验小波变换的频带分割Fig.1 Band splitting of empirical wavelet transform

划分的N个连续区间Λn满足下式：

Λn=[wn-1,wn]n=1,2,…,N

(1)

(2)

确定频带支撑区间Λn后，GILLES等[7]根据Meyer小波的构造方法构造的经验小波尺度函数φn(w)和小波函数ψn(w)分别为

(3)

(4)

其中,过渡函数β(x)=x4(35-84x+70x2-20x3)。

(5)

近似系数通过尺度函数与信号内积产生：

(6)

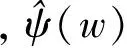
(7)

1.2 能量聚集度经验小波变换(EA-EWT)

EA-EWT算法在EWT的理论框架下，结合小波分析理论与能量聚集度理论实现信号自适应分解。为了衡量时频分析法的能量聚集度，引入频带能量聚集度概念，频带能量聚集度定义为位于区间R中的信号平均能量与位于区间R外的平均能量的比值。时频分析法的能量聚集度CM定义为

(8)

k=s,2s,…,maxs

其中，average()为求平均值函数，TFR(*,*)为时频域函数，s为最小频率分辨率，区间(t,ω)对应信号频率区间[k-δ,k+δ](δ∈R)，δ为能量聚集度带宽因子。

对于能量聚集度的计算，先对信号进行STFT转换至时频谱，得到信号的时频分布，再对时频域利用式(8)计算k=1s,2s,…,maxs的能量聚集度频率分布，实现时频域至频率-能量域的转换。自适应分割频带方法为:假设将频域支撑[0,π]分割成N个连续的部分，用wi表示各片段之间的边界，如图2所示，每段可以表示为

Λi=[wi-1,wi]i=1,2,…,N

(9)

(10)

图2 EA-EWT频带分割Fig.2 Band splitting of EA-EWT

图3 EA-EWT算法流程图Fig.3 Flow chart of EA-EWT algorithm

1.3 最大峭度-包络谱熵筛选准则

周期性冲击信号是齿轮局部故障的主要特征，峭度系数Kp对微弱冲击信号敏感，通常作为敏感分量的筛选指标，其表达式为

(11)

其中，p(x)表示信号x的概率密度。当齿轮箱出现早期故障时，峭度指标中x4因子使分子增大更快，分母增大相对缓慢；而故障严重时冲击成分迅速增加使得Kp中的分母系数增大更快，使得峭度系数反而减小。

包络谱分析为机械故障诊断领域常用方法，包络谱熵为包络谱复杂度衡量指标，故障周期性越明显时，信号包络谱熵值就越小，包络谱熵计算公式为

(12)

其中，(p1,p2,…,pn)为包络谱信号的幅值概率密度。为了克服上述将峭度作为筛选指标的不足，提出一种最大峭度-包络谱熵指标。考虑到随着冲击成分的增加，峭度与包络谱熵的降低速率不一致，为了实现最大峭度-包络谱熵指标随着周期性冲击分量增强而增大，引入了参数σ，记最大峭度-包络谱熵为Kσ，有

Kσ=(Kp)σ/SE

(13)

1.4 最小熵解卷积降噪方法

最小熵解卷积(minimum entropy deconvolution，MED)的目的是通过建立最优滤波器组消除噪声影响，使解卷积的结果突出周期性脉冲信号，此特性尤其适合齿轮箱故障诊断。设齿轮箱局部故障时振动信号离散表达式为

y(n)=h(n)*x(n)+e(n)

(14)

式中，y(n)为测量的振动加速度信号;x(n)为输入的周期冲击信号;e(n)为噪声信号。

(15)

(16)

可得到

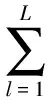
(17)

ω=A0R(y)-1R(x3,y)

(18)

2 诊断算法设计

根据上述分析，为增强故障特征，提出基于EA-EWT和MED的齿轮箱早期故障诊断方法，算法实现流程设计如下：

(1)采用EA-EWT实现振动信号的自适应分解，得到具有物理意义的多分量振动信号。

(2)对分解的多分量信号采用基于最大峭度-包络谱熵(Kσ)准则进行选择，选取Kσ最大的分量。

(3)对选择出的敏感分量进行最小熵解卷积，进一步消除噪声影响突出冲击成分，实现故障特征增强。

(4)对降噪后的信号进行包络解调分析，通过故障特征频率识别进行齿轮箱故障诊断。

3 仿真分析

为验证本文提出的能量聚集度经验小波变换的优越性，构造仿真信号，分别与EMD、EWT方法进行对比，验证所提出方法的可行性和有效性。仿真信号x(t)由调幅调频成分x1(t)、x2(t)、x3(t)三部分组成，信号时频谱如图4所示，信号采样频率设置为4096 Hz，连续采样时间为1 s,即

(19)

(a)仿真信号时域图

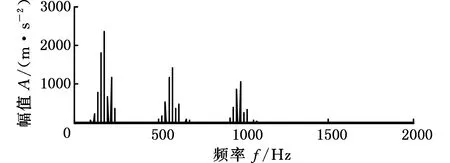
(b)仿真信号频域图图4 仿真信号时频谱Fig.4 Simulation signal time-frequency spectrum

图5所示为EWT自适应频带划分，频带数量为4，EWT按照傅里叶变换峰值将x1(t)分成两个分量，却将x2(t)和x3(t)划分成一个分量。图6所示为不同频段的EWT分解得到的时域信号，由于机械故障中的故障特征一般为边频带特征体现，所以采用EWT频带划分方法易损失故障特征信息。

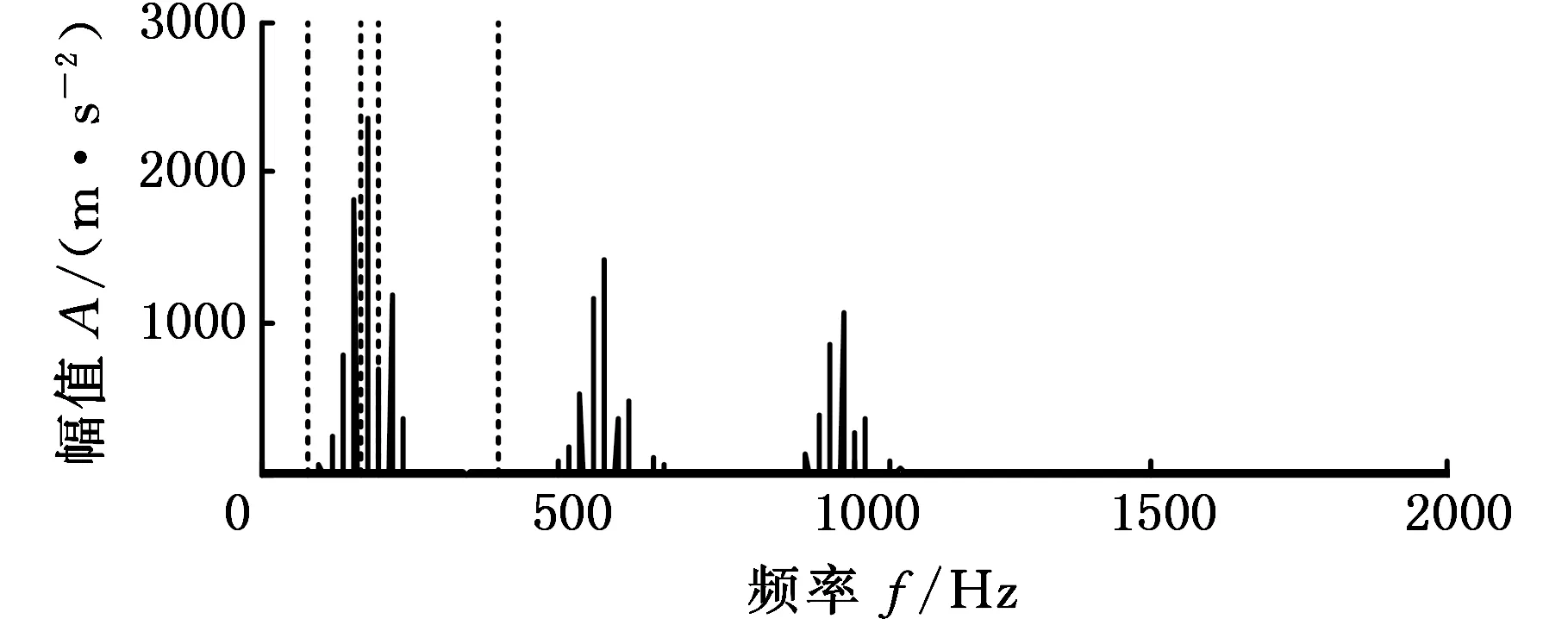
图5 EWT自适应频带划分 Fig.5 EWT adaptive frequency division

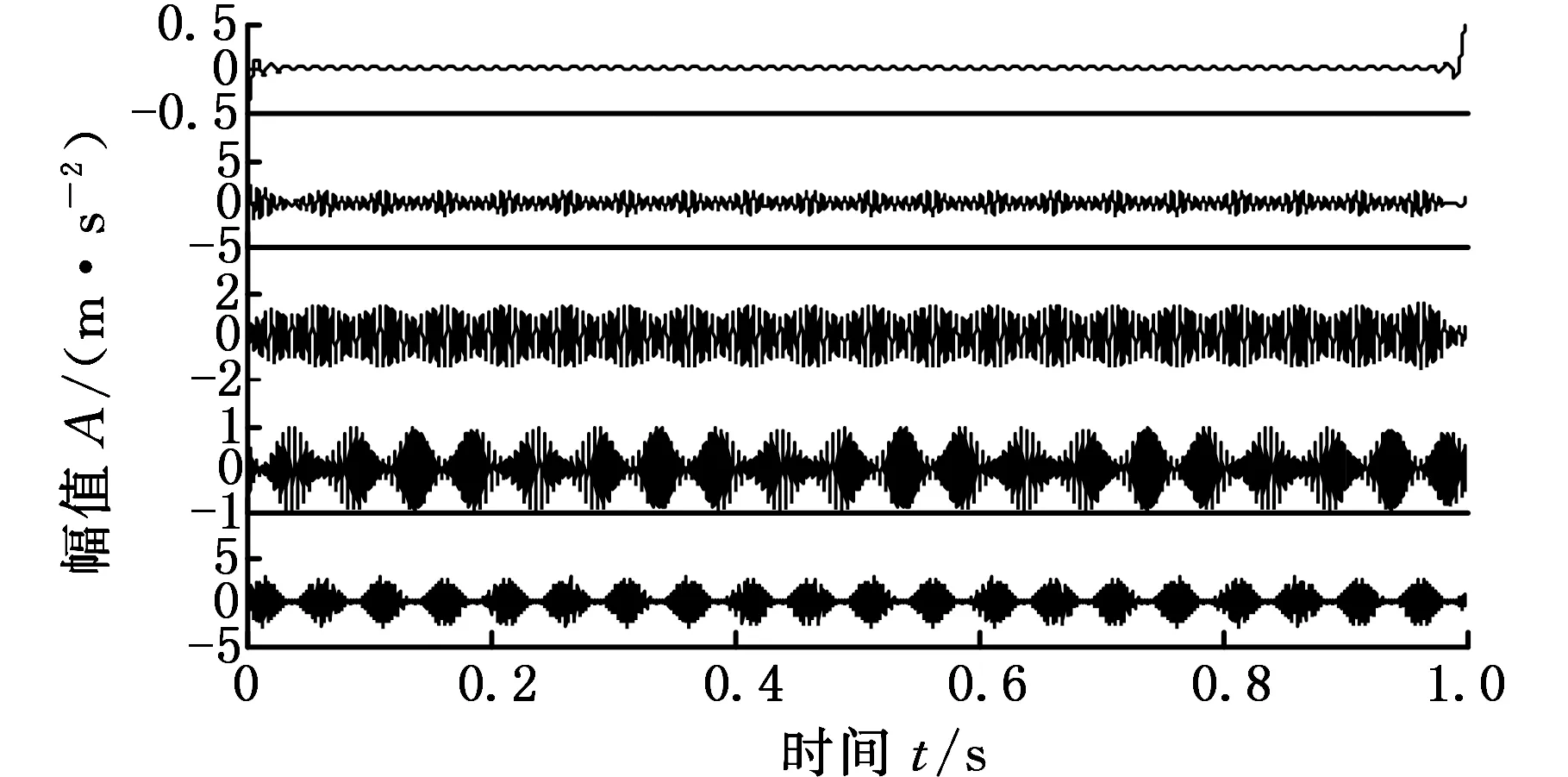
图6 EWT分解结果图Fig.6 Decomposition results of EWT

由EMD自适应分解得到的多分量信号如图7所示。EMD分解得到12个模态分量IMF，其中分量CIMF1不仅包含以200 Hz为频率中心的分量x1,同时包括分量x2和x3，出现了多模态分量的混叠，而CIMF5～CIMF12均为产生的过多的模态分量。

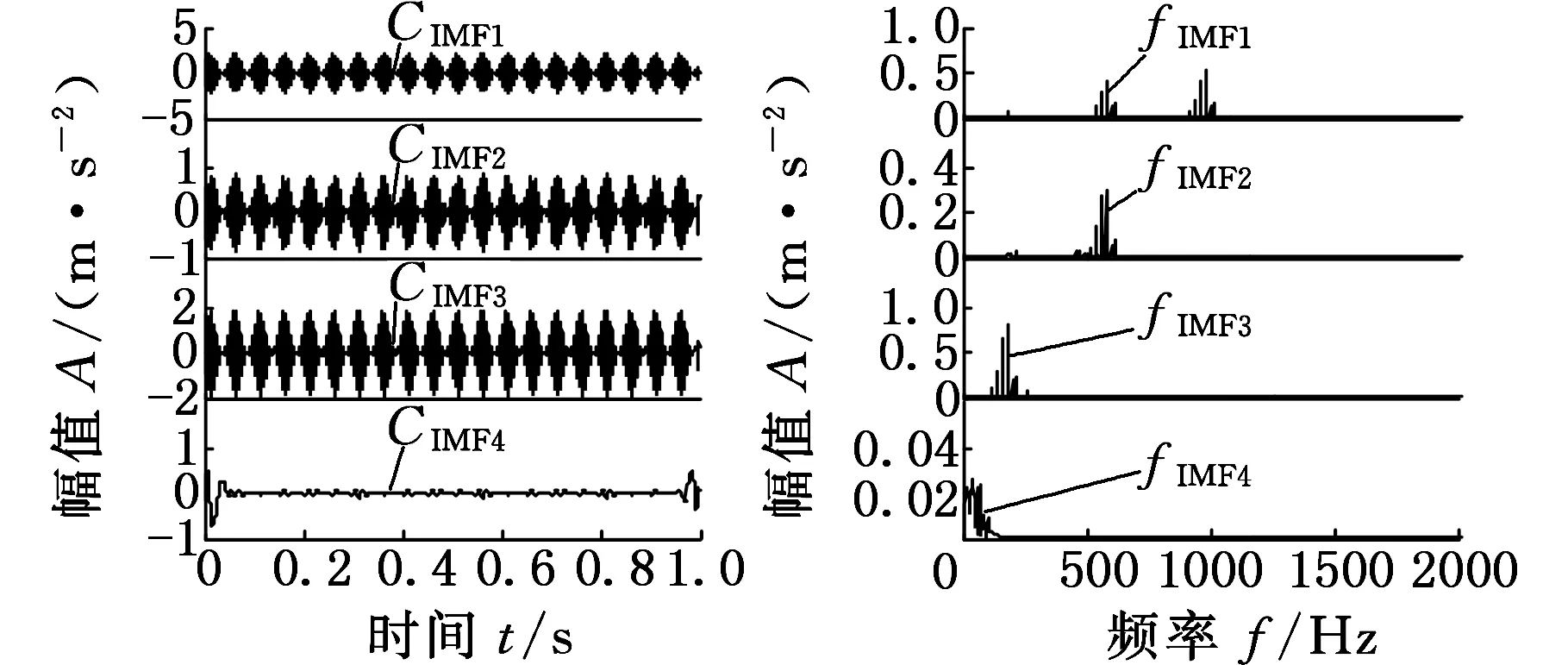
(a)1～4模态分量时频图

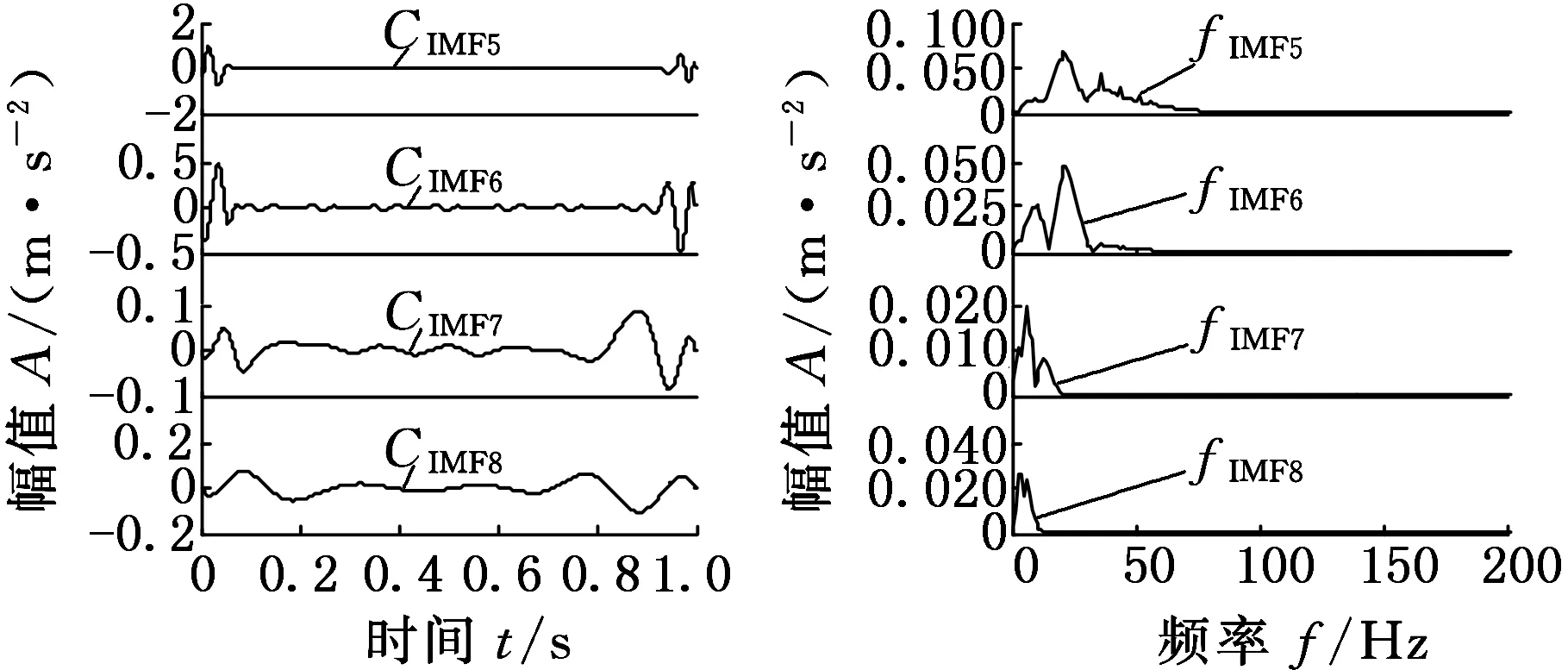
(b)5～8模态分量时频图

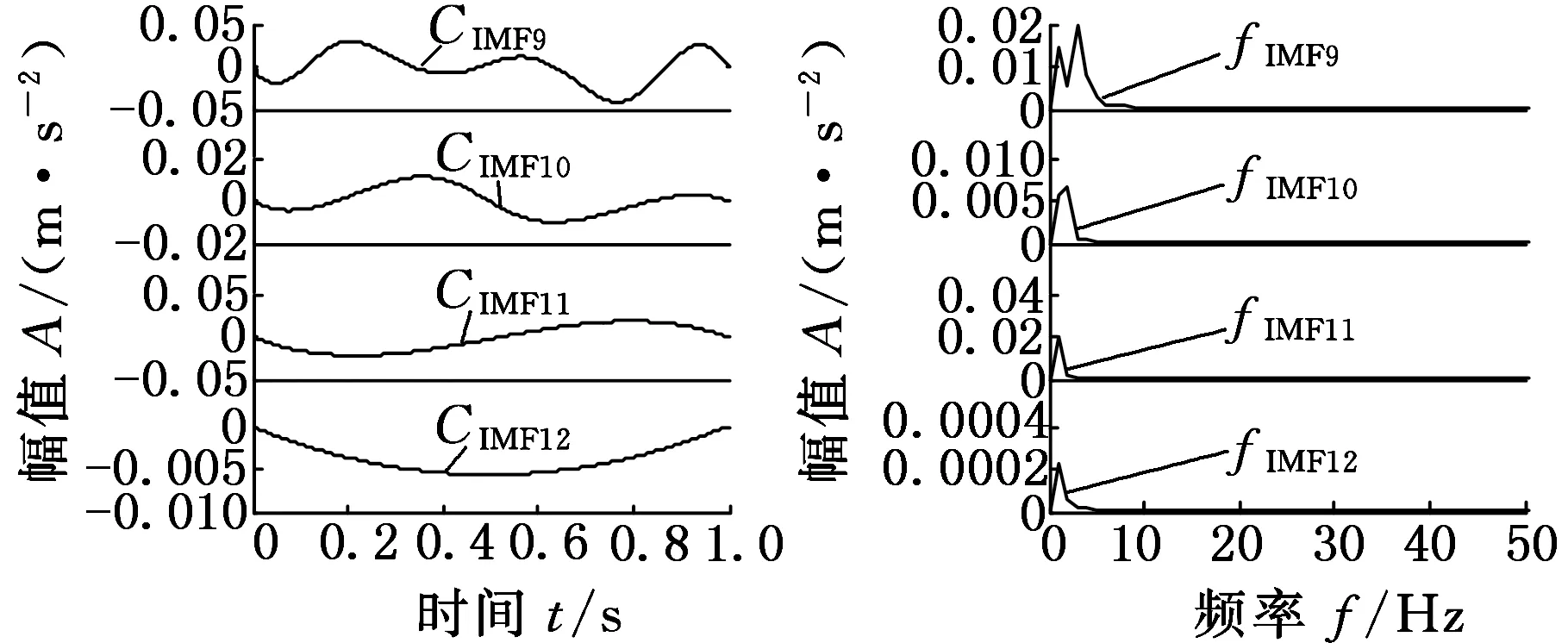
(c)9～12模态分量时频图图7 EMD分解结果图Fig.7 Decomposition results of EMD

图8所示为EA-EWT方法检测出的支撑边界，由图8可以看出,EA-EWT将振动信号按能量聚集度自适应地确定3条频率分割线，划分频率区间，区间的频率中心分别对应200 Hz、600 Hz、1000 Hz，与实际给定信号一致。图9所示为采用EA-EWT分解得到的结果，其中4个分量中c2、c3、c4分别对应给定信号中的x1、x2、x3，c1为残余分量信号。

图8 EA-EWT频带边界Fig.8 EA-EWT band boundary

图9 EA-EWT分解结果图Fig.9 Decomposition results of EA-EWT

综上分析可得：EA-EWT方法可以自适应分解信号，同时消除模态混叠，保留边频带信息，适合于齿轮箱故障诊断。

4 试验

4.1 试验说明

试验在QPZZ-Ⅱ旋转机械振动分析及故障诊断试验平台上完成。试验平台由变速驱动电机、多功能可编程控制面板、齿轮传动齿轮箱、磁粉制动器、压电式加速度传感器、转速传感器、数据采集器等构成。整个系统固定在底座上，由交流异步变频电机(功率750 W，转速控制范围为0～1500 r/min)提供动力作为输入端，驱动电机和磁粉制动器由不同的调节器来控制，用以调整不同转速和负载，并控制加载时间，实现模拟不同工况，试验平台结构见图10。试验平台主动齿轮齿数z1=55，从动齿轮齿数z2=75。加速度传感器安装于齿轮箱顶部，采样频率设置为5120 Hz，给定输入轴转速为880 r/min，采集大齿轮正常与点蚀状态下的振动加速度信号，为了更加接近实际情况，加入-1dB噪声，进行对比分析。

图10 齿轮箱试验平台Fig.10 Gearbox test rig

4.2 试验信号分析

齿轮点蚀是常见的齿轮箱早期故障，对齿轮点蚀故障进行试验分析，选取数据长度为5120点。

图11为齿轮点蚀故障振动信号时频域波形图，从图11a中可看到明显的冲击信号，但无法判别齿轮故障信息。为对比分析，首先采用EWT方法进行分解，指定频带数N=15，图12所示为EWT的频带划分区间，频谱分量集中于啮合频率500 Hz处，此时易使故障特征信号丢失，而在高频区间划分为一个分量，此时无法提取微弱的故障特征信息。

(a)点蚀故障时域图

(b)点蚀故障频域图图11 点蚀故障振动信号波形图Fig.11 Waveform of pitting fault vibration signal

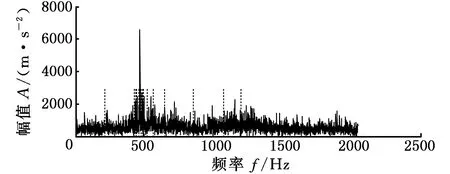
图12 点蚀故障EWT频带划分Fig.12 Pitting fault frequency division of EWT

用本文方法对振动信号采用EA-EWT分解，设置频率聚集度因子δ=10，分解后得到频带划分如图13所示，能得到24个单分量信号。

对于EA-EWT分解得到的单分量，采用最大峭度-包络谱熵准则进行敏感分量筛选，通过分析数据，设置σ=1/3时取得较好的效果，因此设置Kσ的σ=1/3，筛选得到系数最大的分量为分量11，分量11的时域信号如图14所示。图14中，筛选出的敏感分量中可见冲击特征明显，对比图11的原振动信号，体现了本文所提出方法的优越性。对筛选出的分量信号采用最小熵解卷积降噪，设置迭代次数M=100，滤波器L=120，如图15所示。图15相比图14，噪声干扰成分基本得到消除，使得冲击成分更加明显，相邻冲击分量的时间间隔为Δt，对应故障特征频率为fr。

图13 点蚀故障EA-EWT频带划分Fig.13 Pitting fault frequency division of EA-EWT

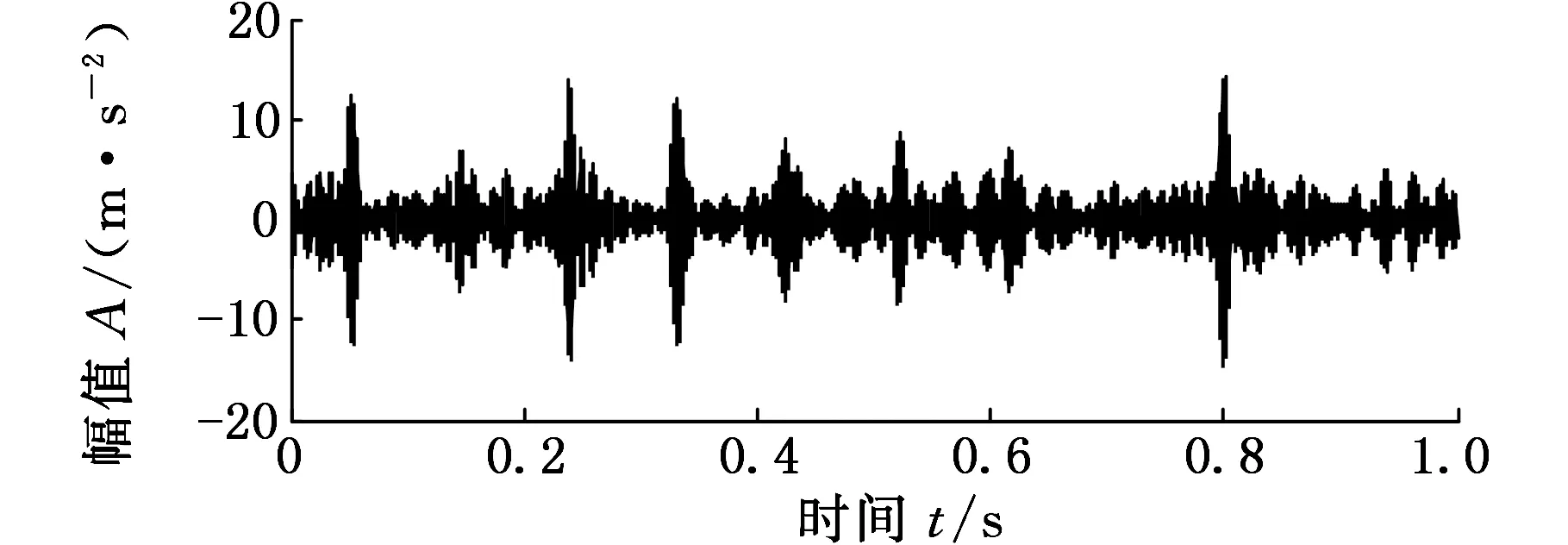
图14 Kσ最大系数分量信号Fig.14 Time signal of Maximum coefficient

图15 MED降噪后信号Fig.15 Noise reduction signal of MED

对降噪后信号进行包络谱解调分析。在试验中设定转速ns=880 r/min，即转频fs=14.667 Hz，主动齿轮齿数z1=55，从动齿轮齿数z2=75，从动齿轮故障特征频率fr=10.75 Hz，其包络谱如图16所示。从图16中明显可见，故障特征频率fr及其倍频出现了明显的峰值分量，这对应周期性冲击成分所对应的频率段，由此能判断从动齿轮发生了局部故障。

图16 点蚀故障包络谱Fig.16 Envelope spectrum of pitting fault

5 结论

(1)针对齿轮箱发生早期故障问题，提出了一种基于能量聚集度经验小波变换的齿轮箱故障诊断算法，仿真分析与试验结果证明了此方法是可行有效的。

(2)该方法融合EMD、小波变换和EWT的优点，引入能量聚集度指标，指定能量聚集度带宽因子δ，获得有限的能量聚集度极值点，根据能量聚集度极值点自适应地计算分解频带数量与频带宽度，该方法避免了模态混叠与虚假分量。

(3)该方法能较好地保留振动信号边频带信息，增强故障特征信息，适用于齿轮箱早期故障诊断。

[1] 李志农, 朱明, 褚福磊,等. 基于经验小波变换的机械故障诊断方法研究[J]. 仪器仪表学报, 2014,35(11):2423-2432. LI Zhinong, ZHU Ming, CHU Fulei, et al. Mechanical Fault Diagnosis Method Based on Empirical Wavelet Transform[J]. Chinese Journal of Scientific Instrument,2014,35(11):2423-2432.

[2] 雷亚国, 孔德同, 李乃鹏, 等. 自适应总体平均经验模式分解及其在行星齿轮箱故障检测中的应用[J]. 机械工程学报,2014,50(3):64-70. LEI Yaguo, KONG Detong, LI Naipeng, et al. Adaptive Ensemble Empirical Mode Decomposition and Its Application to Fault Detection of Planetary Gearboxes[J]. Journal of Mechanical Engineering,2014,50(3):64-70.

[3] 唐贵基, 王晓龙. 参数优化变分模态分解方法在滚动轴承早期故障诊断中的应用[J]. 西安交通大学学报,2015,49(5):73-81. TANG Guiji,WANG Xiaolong. Parameter Optimized Variational Mode Decomposition Method with Application to Incipient Fault Diagnosis of Rolling Bearing[J]. Journal of Xi’an Jiao Tong University,2015,49(5):73-81.

[4] 胥永刚, 赵国亮, 侯少飞, 等. DT-CWT相关滤波在齿轮箱故障诊断中的应用[J]. 振动.测试与诊断,2016,36(1):138-144. XU Yonggang, ZHAO Guoliang, Hou Shaofei, et al. DT-CWT Domain Correlation Filter and Its Application Incipient Gearbox Fault Diagnosis[J]. Journal of Vibration,Measurement&Diagnosis,2016,36(1):138-144.

[5] DAUBECHIES I, LU J, WU H T. Synchrosquee-zed Wavelet Transforms: an Empirical Mode Decomposition-like Tool[J]. Applied & Computational Harmonic Analysis,2011,30(2):243-261.[6] DRAGOMIRETSKIY K, ZOSSO D. Variational Mode Decomposition[J]. IEEE Tran. on Signal Processing,2014,62(3):531-544.

[7] GILLES J. Empirical Wavelet Transform[J]. IEEE Transactions on Signal Processing,2013,61(16):3999-4010.

[8] AMEZQUITA-SANCHEZ J P, ADELI H. A New Music-empirical Wavelet Transform Methodology for Time-Frequency Analysis of Noisy Nonlinear and Non-stationary Signals[J]. Digital Signal Processing, 2015,45(C):55-68.

[9] KEDADOUCHE M, LIU Z, VU V H. A New Approach Based on OMA-empirical Wavelet Transforms for Bearing Fault Diagnosis[J]. Measurement,2016,90:292-308.

[10] KEDADOUCHE M, THOMAS M, TAHAN A. A Comparative Study between Empirical Wavelet Transforms and Empirical Mode Decomposition Methods: Application to Bearing Defect Diagnosis[J]. Mechanical Systems&Signal Processing,2016,81:88-107.

[11] CHEN J, PAN J, LI Z, et al. Generator Bearing Fault Diagnosis for Wind Turbine via Empirical Wavelet Transform Using Measured Vibration Signals[J]. Renewable Energy,2016,89:80-92.

(编辑 王艳丽)

Early Weak Fault Diagnosis of Gearboxes Based on Energy Aggregation and EWT

WANG Youren CHEN Wei SUN Canfei SUN Quan HUANG Haian

College of Automation Engineering, Nanjing University of Aeronautics and Astronautics,Nanjing,211106

For the early faults of gearboxes, the fault features were not obvious, and the vibration signals were nonlinear and non-stationary, a method was proposed based on energy aggregation and EWT (EA-EWT). Vibration signals were decomposed by EA-EWT, and the maximum kurtosis envelope spectrum entropy criterion was used to filter the sensitive signals. For the selected signals, the minimum entropy deconvolution was used to reduce the noise. The Hilbert envelope spectrum of the signals was analyzed after noise reduction, and the fault types were identified by the frequency components in the envelope spectrum to realize the early fault diagnosis. The experimental results show that the new method may significantly enhance the early weak fault characteristics and improve the early fault diagnosis performances.

empirical wavelet transform(EWT); maximum kurtosis and envelope spectrum entropy; gearbox; fault diagnosis

2016-07-20

国家商用飞机制造工程技术研究中心创新基金资助项目(SAMC14-JS-15-01);航空科学基金资助项目(2013ZD52055)

TH113

10.3969/j.issn.1004-132X.2017.12.015

王友仁，男，1963年生。南京航空航天大学自动化学院教授。主要研究方向为航空综合测试、故障诊断与健康预报。陈 伟(通信作者)，男，1991年生。南京航空航天大学自动化学院硕士研究生。E-mail:weichen_cole@126.com。孙灿飞，男，1979年生。南京航空航天大学自动化学院博士研究生。孙 权，男，1988年生。南京航空航天大学自动化学院博士研究生。黄海安，男，1992年生。南京航空航天大学自动化学院硕士研究生。