金属带式无级变速器带轮变形损失研究

傅 兵 周云山 高 帅 李 泉 安 颖.湖南大学汽车车身先进设计制造国家重点实验室，长沙，4008.湖南江麓容大车辆传动股份有限公司，长沙，4005



金属带式无级变速器带轮变形损失研究

傅 兵1周云山1高 帅2李 泉1安 颖1
1.湖南大学汽车车身先进设计制造国家重点实验室，长沙，4100822.湖南江麓容大车辆传动股份有限公司，长沙，410205

为了减少金属带式无级变速器变速机构的传动损失，分析了带轮变形损失机理，推导出带轮变形损失计算模型。基于某国产无级变速器的实际参数，引入由有限元方法建立的带轮轴向变形模型，定量分析了带轮变形所导致的楔入损失及进出口损失，获得了金属带速比、输入转矩对带轮变形损失的影响规律。分析结果表明：带轮变形损失随输入转矩的增大而增大，在最小速比和最大速比位置的损失大于中间速比位置的损失，其中楔入损失是构成带轮变形损失的主要部分；可通过提升带轮在最大工作半径处的等效轴向刚度来减小变形损失。最后通过台架试验验证了变形损失计算模型的可信性。

无级变速器；带轮变形；转矩损失；传动效率

0 引言

金属带式无级变速器(continuously variable transmission，CVT)能够连续改变速比,使发动机持续工作在最佳经济点，装配CVT的汽车在燃油经济性上具有优势，但CVT变速机构的传动形式是摩擦传动，它存在摩擦损失，变速机构的传动效率直接影响CVT的应用效能，如何搭建合适的模型来分析CVT变速机构的传动损失一直是CVT研究的热点[1-2]。变速机构的传动损失由钢环摩擦损失、金属带与带轮之间的滑移损失、金属带楔入损失及进出口损失等部分构成，其中，金属带楔入损失及进出口损失与带轮变形有关，统称为带轮变形损失，是变速机构传动损失的重要组成部分[3]。为了优化带轮设计，提升CVT的传动效率，必须弄清带轮变形损失的变化规律。

KIM等[4]通过试验证实了带轮变形引起的金属带运行轨迹变化及损失的存在。MICKLEM等[5]提出了一种半经验模型来估算带轮变形所导致的转矩损失，在特定条件下的估算结果与试验结果吻合较好。张晓冰等[6]基于瞬态动力学理论分析了带轮变形对传动损失的影响，但没有取得量化的损失数据。由于带轮实际变形难以用解析方式描述，故目前计算带轮变形损失大多是使用经验或半经验模型，只有AKEHURST[7]基于带轮变形的近似测量数据，计算了最小速比和最大速比位置的变形损失，但没有基于系统的带轮变形模型进行分析及验证。本文分析了带轮变形损失机理，推导出带轮变形损失模型，基于以某CVT实际参数建立的带轮轴向变形模型，定量分析了带轮变形所导致的金属带楔入损失及进出口损失，揭示了金属带速比、输入转矩对带轮变形损失的影响规律，最后通过台架试验对分析结果进行了验证。

1 带轮变形损失模型

1.1 带轮变形损失原理

CVT变速机构由主动带轮、从动带轮及金属带构成，主从动带轮分别包含一固定锥盘和一可动锥盘，如图1所示。变速机构通过两可动锥盘的轴向移动来改变金属带与两带轮锥面间的接触半径，从而实现速比的无级变化。

图1 CVT变速机构实物模型Fig.1 Practicality model of CVT variator

CVT运行时，可动锥盘端部的液压缸提供夹紧力来保证金属带传递转矩。由于金属带轴向刚度远大于带轮的轴向刚度，故金属带受挤压产生的反作用力使两锥盘发生变形。带轮变形后，金属带由理想位置滑移到实际位置，这使得金属带的工作半径发生变化，具体如图2所示。

图2 带轮变形示意图Fig.2 Schematic of pulley deflection

由于带轮工作半径上的轴向变形在包角范围内是一变化值，所以金属带在带轮上的实际运行轨迹不再是理想圆弧。从包角入口位置到包角出口位置，金属带在径向方向是逐渐楔入带轮，而离开带轮时是逐渐楔出带轮，金属带在包角区域与带轮的径向滑动所产生的摩擦损失为楔入损失。受到包角进出口处带轮轴向变形的影响，金属带进入带轮时需克服入口处的轨迹偏移，提前与带轮接触，直至进入理想包角入口;而金属带离开带轮时需克服出口处轨迹偏移，延缓了与带轮的接触，直至带轮变形消失，在进出口处金属带与带轮的摩擦损失统称为进出口损失。

为分析上述损失，基于以下假设建立带轮变形损失机理模型：①金属带轴向为无限刚性；②忽略金属带轴向偏置的影响，认为金属带与两锥盘的接触轨迹一致；③带轮与金属带之间的摩擦因数为恒定值。为便于分析，模型中的各项损失均换算为主动带轮的输入转矩损失。

1.2 楔入损失

以主动带轮为例进行分析。图3所示的金属带运行轨迹示意图中，金属带中的任意一个金属片都是从包角入口A′逐渐楔入到最低点D，然后从D点楔出到包角出口A。假设带轮在D、A点所对应的理想轨迹点的轴向变形分别为δp1、δp2，根据图4所示的几何关系，相对于理想轨迹所产生的径向位移

hp1=δp1(Rp-Ra)/(δp1+(Rp-Ra)tanβ)

hp2=δp2(Rp-Ra)/(δp2+(Rp-Ra)tanβ)

式中，Rp为主动带轮理想工作半径；β为带轮锥角;Ra为带轮轴半径。

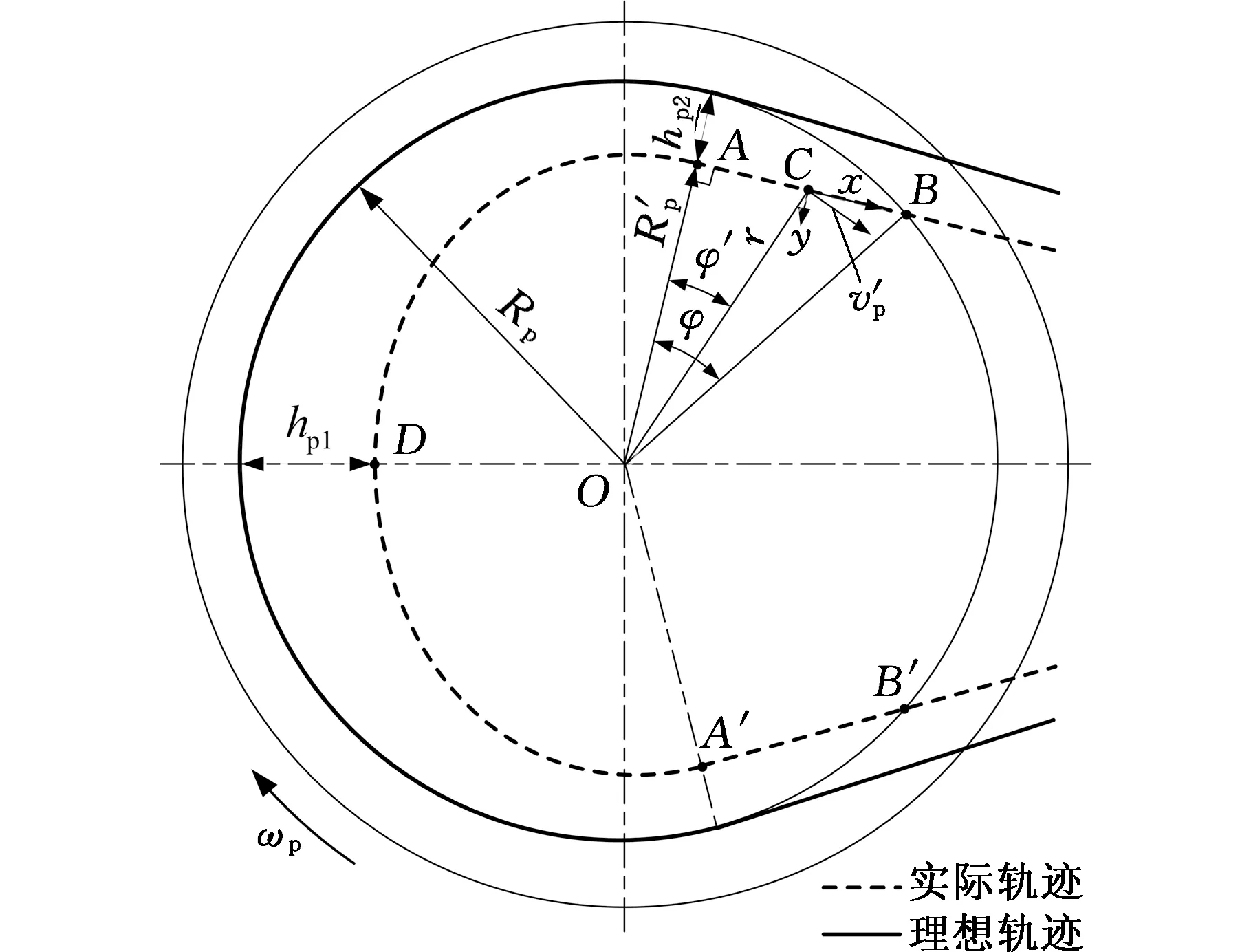
图3 金属带运行轨迹示意图Fig.3 Schematic of the metal belt running path

图4 带轮变形几何关系示意图Fig.4 Geometric schematic of pulley deflection

金属带在包角出口A处的实际工作半径

在金属带实际轨迹上的任意点，单位时间内通过的金属片数目

式中，ωp为主动带轮转速；t为金属片厚度。

由于金属片的两工作面分别与两锥盘接触，单个金属片在楔入及楔出过程中的摩擦功

Wp1=4μNp(hp1-hp2)

式中，μ为金属片与带轮之间的摩擦因数，取固定值0.08[8]；Np为主动带轮上单个金属片所受的正压力。

主动带轮上的楔入损失

由于主从动轮上的楔入损失机理一致，故整个变速机构的楔入损失

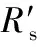
1.3 进出口损失

vy=rωpsinφ′

在该点的相对速度

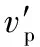
由于r在AB段上是一变化值，在此定义Rpo为AB段相对运动的当量半径，故金属带与带轮在AB段的平均相对速度

vp=ωpRpo

AB段之间的金属片数目

式中，φ为相对运动直线段首尾点与带轮中心连线间的夹角。

由于相对速度的存在，A′B′段存在相同的损失，故主动带轮进出口处的损失

Tp2=2npvpNpμ/ωp=2npRpoNpμ

在从动带轮上的进出口位置也存在类似的摩擦损失。因此，整个变速机构的进出口损失

Tl2=Tp2+Ts2=2npRpoNpμ+2nsRsoNsμ

式中，Ts2为从动带轮进出口损失；ns为从动带轮相对运动直线段上金属片数目；Rso为从动带轮相对运动直线段的当量半径；Ns为从动带轮上单个金属片所受的正压力。

整个变速机构的带轮变形损失

Tl=Tl1+Tl2

1.4 带轮变形损失模型的构建

为了构建系统的变形损失模型，需要将上述损失机理模型与变速机构参数模型相关联。变速机构的几何参数由下式确定：

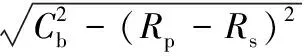
(1)

θp=π+2arcsin((Rp-Rs)/Cb)

(2)

θs=π-2arcsin((Rp-Rs)/Cb)

(3)

式中，L为金属带长度；θp、θs分别为主从动带轮包角；Rs为从动带轮理想工作半径；Cb为带轮中心距。

变速机构的速比定义为

i=Rs/Rp

(4)

稳态工况下从动带轮和主动带轮的夹紧力由下式计算：

Fs=SfTincosβ/(2μRp)

(5)

Fp=fk(i)Fs

(6)

式中，Tin为输入转矩；Sf为安全系数，工程中一般取1.3；fk(i)为主从动带轮夹紧力的比值，通常由试验方式得出[9]。

根据式(1)～式(6)，结合前述损失机理模型，带轮变形损失可表示为输入转矩、速比以及轴向变形的函数：

Tl=f(Tin,i,δ)

带轮轴向变形δ是求解变形损失的关键。带轮轴向变形与其所受夹紧力及工作半径有关，而稳态工况下的夹紧力及工作半径由输入转矩及速比确定。因此，可将带轮轴向变形表示为输入转矩和速比的函数：

δ=f(Tin,i)

(7)

通过式(7)所描述的带轮轴向变形模型，带轮变形损失可转化为输入转矩及速比的函数：

Tl=f(Tin,i)

2 带轮轴向变形模型

本文以某国产CVT为研究对象构建带轮轴向变形模型，其变速机构参数见表1。定义速比序列：0.44,1.00,1.50,2.00,2.43，输入转矩序列：30,60,90,120,150 N·m。将以上速比及输入转矩序列进行正交组合得到工况样本，通过有限元方法来计算各工况下的主从动带轮的轴向变形。各工况下的载荷可根据式(1)～式(6)及表1计算得到。

表1 变速机构参数

Tab.1 Variator parameter

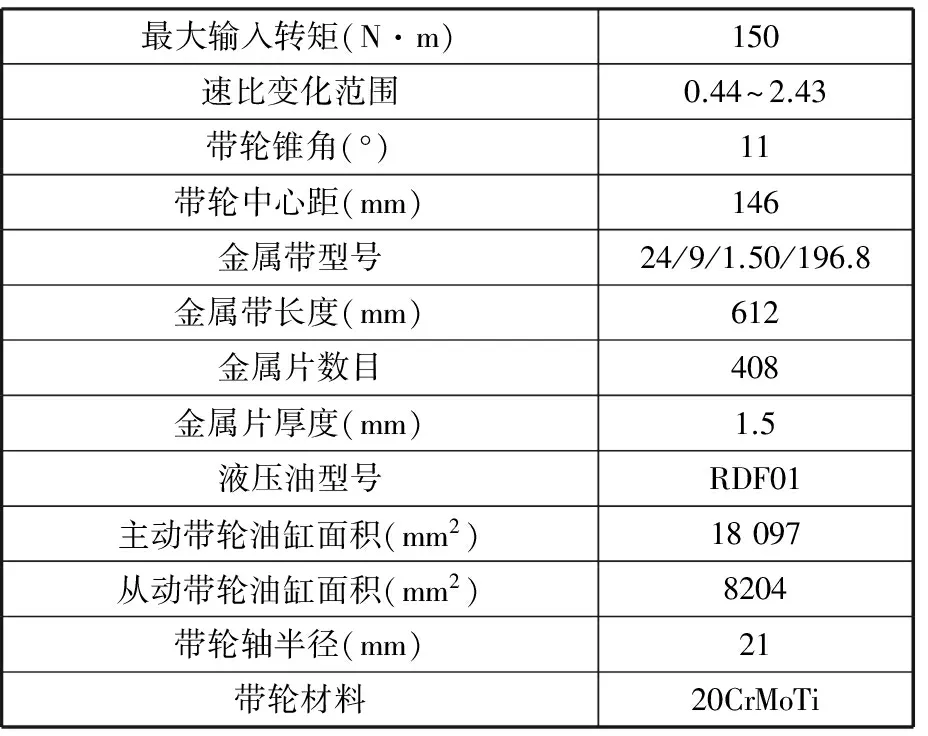
最大输入转矩(N·m)150速比变化范围0．44～2．43带轮锥角(°)11带轮中心距(mm)146金属带型号24/9/1．50/196．8金属带长度(mm)612金属片数目408金属片厚度(mm)1．5液压油型号RDF01主动带轮油缸面积(mm2)18097从动带轮油缸面积(mm2)8204带轮轴半径(mm)21带轮材料20CrMoTi

带轮有限元模型如图5所示。为保证计算精度，使用映射网格划分的方式进行划分。根据带轮的实际受力情况，将金属带的反作用力转化为节点力载荷施加在工作半径区域，在活动锥盘端部的油缸内施加压力载荷，在两端轴承位置处施加固定约束。

图5 带轮有限元模型Fig.5 FE model of pulley

图6为带轮变形云图，在金属带反作用力的作用下，包角区域的两锥盘反向张开，锥角呈增大趋势；另一端的非包角区域，两锥盘同向靠拢，锥角呈减小趋势，这与文献[7]中的带轮外缘轴向位移测试结果所体现的变形趋势是一致的。定义使锥角增大的变形为正向变形，使锥角减小的变形为负向变形，同时以带轮非包角区域中心线为0°基点，提取两锥盘工作半径轨迹圆上各节点的轴向位移的平均值作为带轮轴向变形值，轨迹圆坐标定义如图7所示。

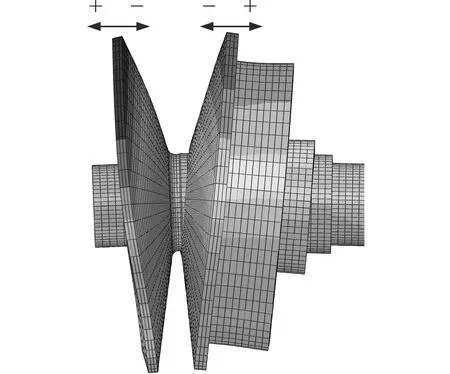
图6 带轮变形云图Fig.6 Deformation contour of pulley

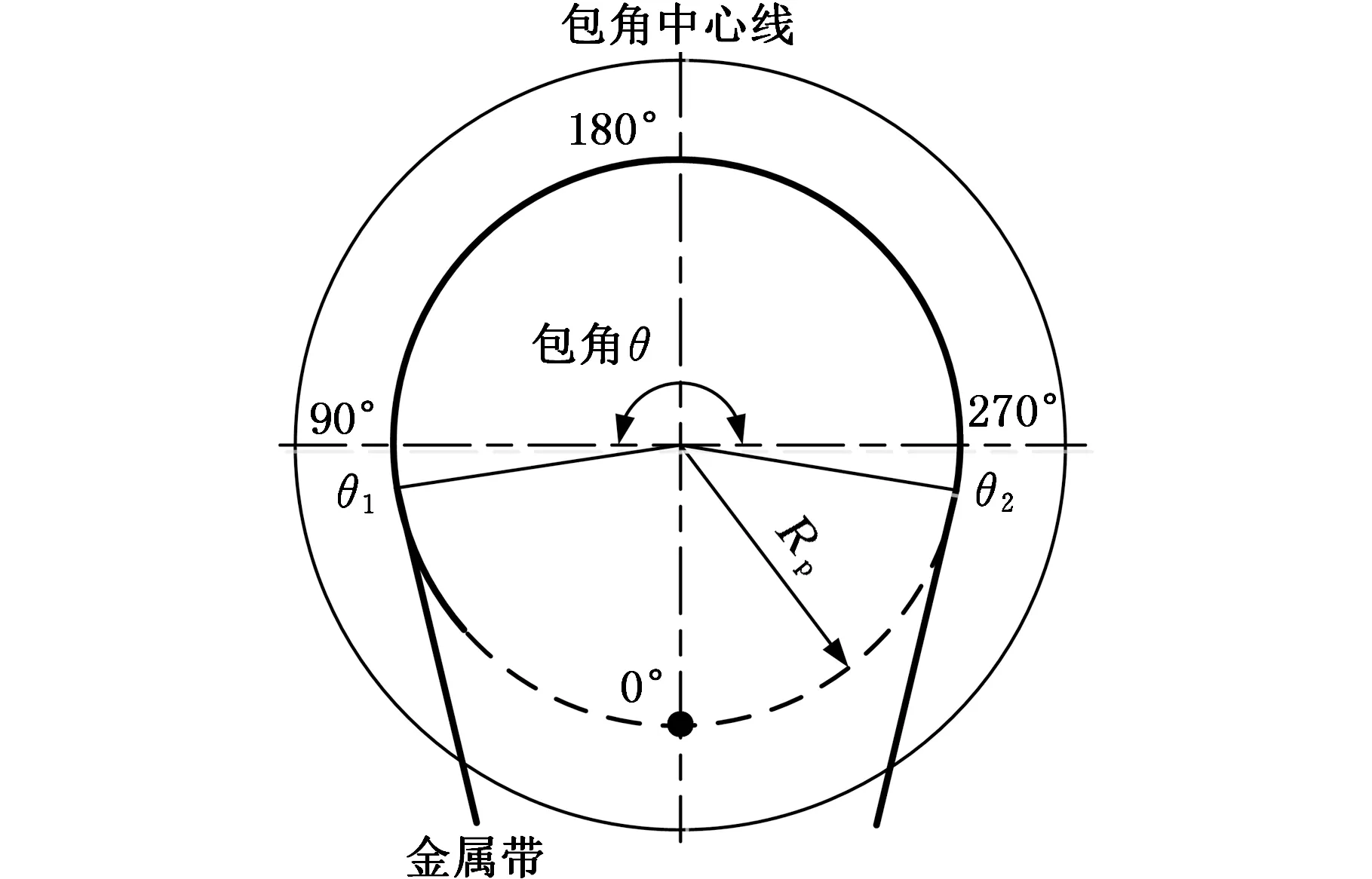
图7 工作半径轨迹圆示意图Fig.7 Schematic of pulley working circle

图8所示为带轮工作半径处轨迹圆的轴向变形曲线。轨迹圆上的变形以包角中心线为轴对称分布，最大正向变形出现在包角中心位置，计算带轮变形损失所需的δp1及δp2可从带轮变形曲线中获得。主从动带轮的轴向变形数据模型分别如图9、图10所示。

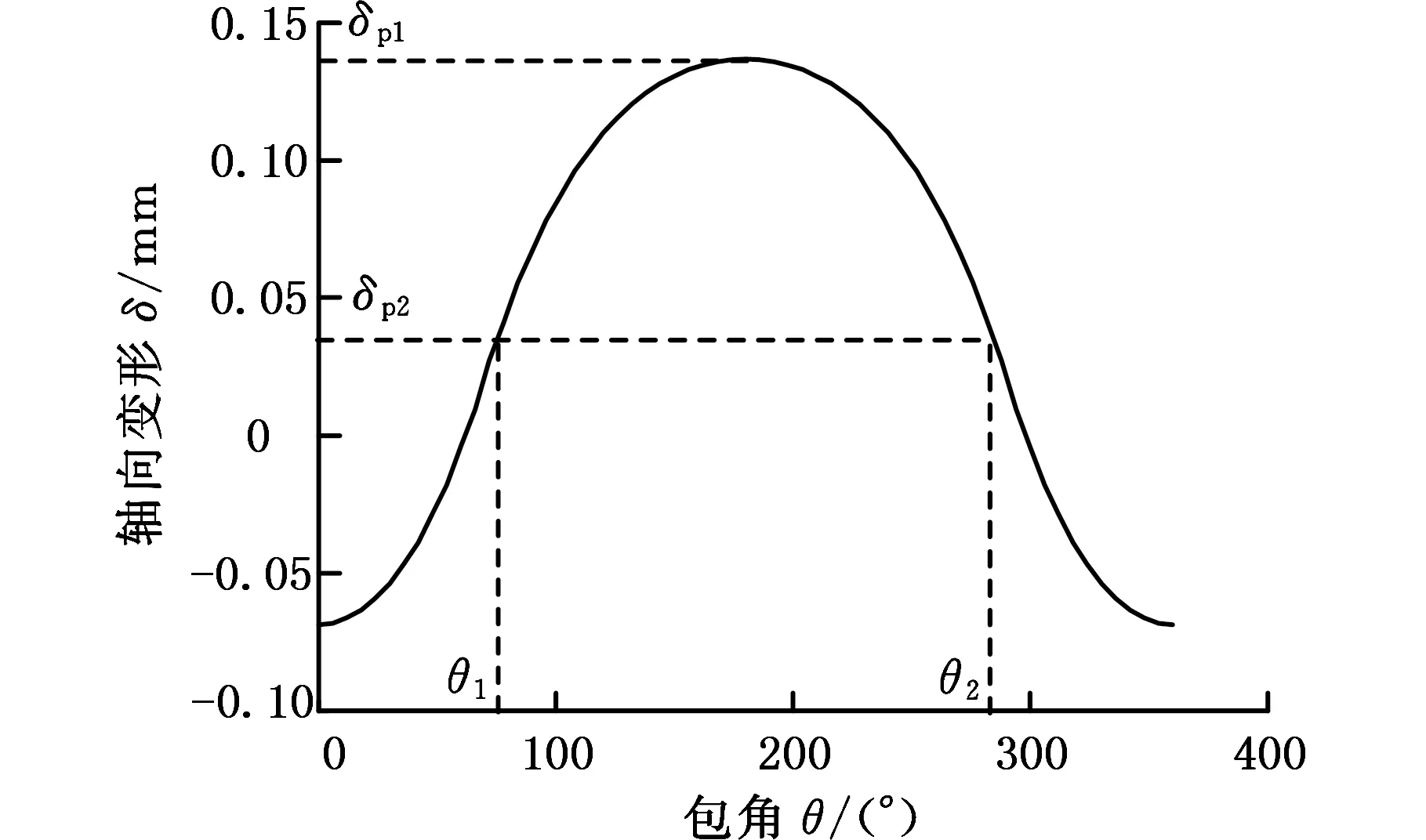
图8 i=2.43，Tin=150 N·m时主动带轮工作半径轨迹圆轴向变形Fig.8 Axial deflection of primary pulley at working circle(i=2.43,Tin=150 N·m)

图9 主动带轮轴向变形与速比及输入转矩的关系Fig.9 Axial deflection of primary pulley against speed ratio and input torque

图10 从动带轮轴向变形与速比及输入转矩的关系Fig.10 Axial deflection of secondary pulley against speed ratio and input torque

3 计算结果分析

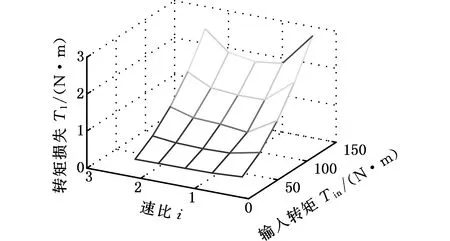
图11 转矩损失与速比及输入转矩的关系Fig.11 Torque loss against speed ratio and input torque

图11是变形损失与速比及输入转矩的关系图。从输入转矩坐标来看，变形损失随输入转矩的增大而增大。输入转矩为30 N·m时，变形损失在0.5 N·m以内；输入转矩为150 N·m时，各速比下的变形损失增大到1.7～2.7 N·m。这是因为速比一定时，作用在带轮上的夹紧力与输入转矩成正比，夹紧力的增大一方面导致金属带与带轮之间的摩擦力增大，另一方面造成带轮轴向变形增大，这使得金属带在带轮上的楔入距离及进出口处的相对运动距离增加，所以转矩损失随之增大。从速比坐标上分析，整个曲面呈内凹状，即在最大速比和最小速比位置的变形损失较大，中间速比位置的变形损失较小。输入转矩一定时，在最小速比和最大速比位置，主从动带轮的工作半径分别处于最外缘，夹紧力和带轮轴向变形均达到最大，故在这两个速比位置的变形损失大于中间速比位置的损失。

以输入转矩为150 N·m时各速比下的楔入损失及进出口损失数据为例，分析变形损失的构成。由图12可知，各速比下的楔入损失占变形损失的70%以上，是变形损失的主要构成部分。这是因为带轮包角中心位置轴向变形较大，进出口位置的轴向变形较小，金属带楔入过程中的楔入距离大于进出口过程中的相对运动距离。

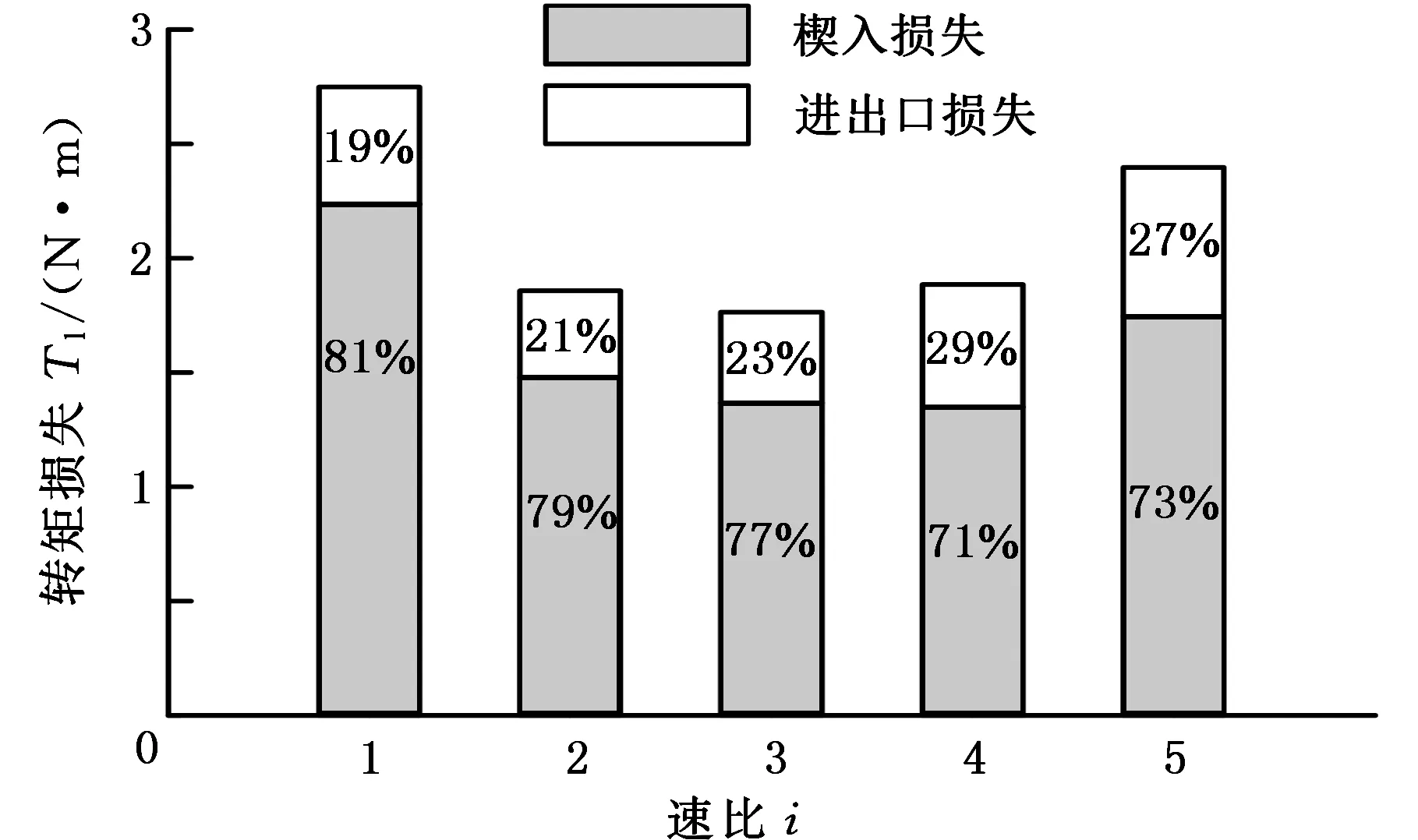
图12 Tin=150 N·m时各速比下的楔入损失及进出口损失Fig.12 Radial penetration loss and the wedge loss in different speed ratio (Tin=150 N·m)

由以上分析可知，带轮包角中心位置的轴向变形是影响变形损失的主要因素。夹紧力一定时，带轮轴向变形的大小由带轮的刚度决定。定义带轮夹紧力与包角中心位置轴向变形的比值为带轮等效轴向刚度。由图13所示的等效轴向刚度与带轮工作半径的关系可知，等效轴向刚度随工作半径的增大而减小，带轮在最大工作半径处的等效轴向刚度最小，轴向变形最大。因此，可通过提升带轮在最大工作半径处的等效轴向刚度来减小带轮轴向变形及变形损失，从而提高变速机构的传动效率。

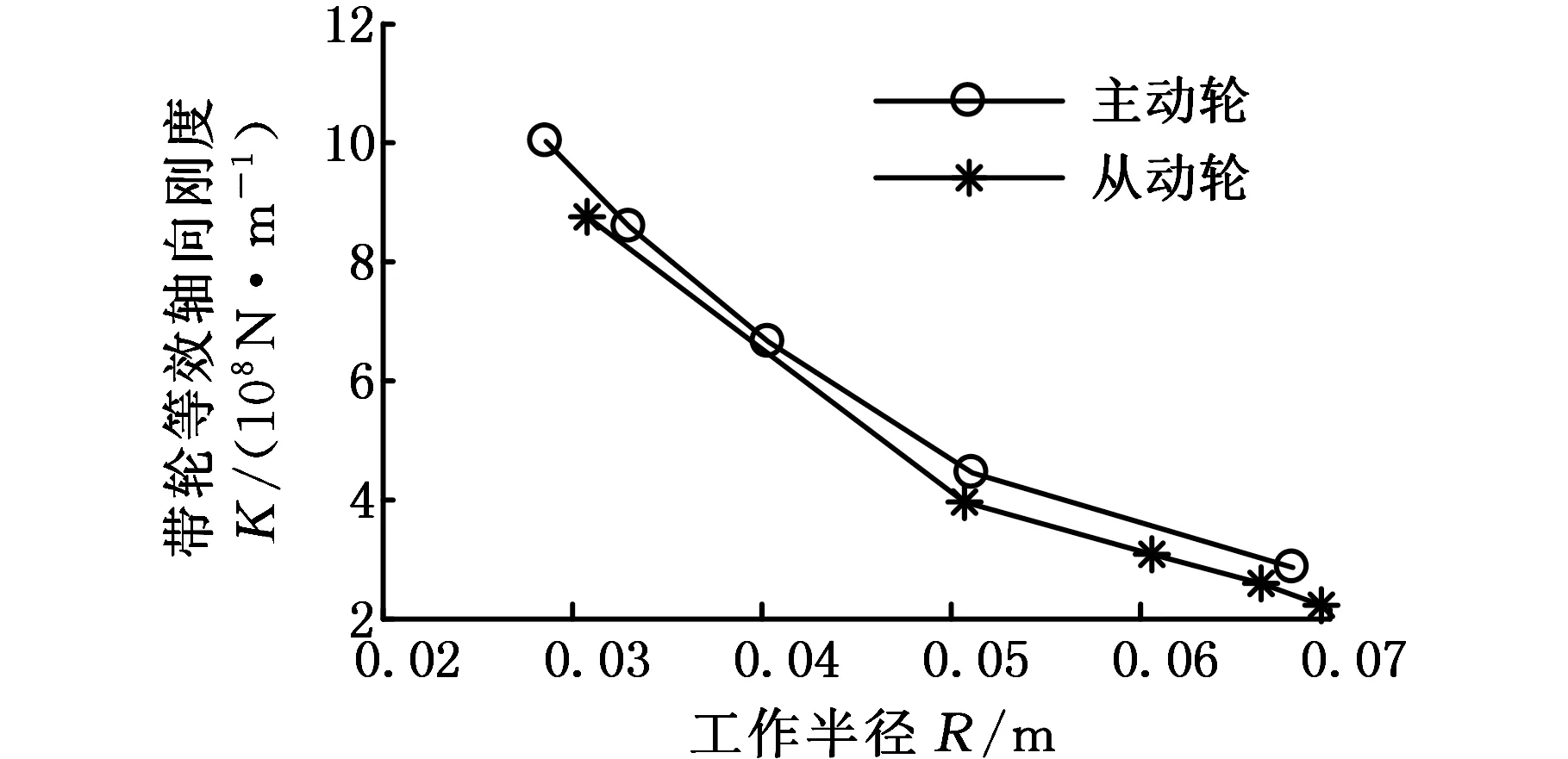
图13 带轮等效轴向刚度与工作半径的关系Fig.13 Relationship between pulley equivalent axial stiffness and working radius

4 试验验证

除带轮变形损失之外，变速机构中还存在滑移损失以及钢环摩擦损失，所以难以直接对变形损失进行精确测试。变速机构在空载工况下，可认为金属带与带轮之间没有滑移损失[10]，而低转速工况下钢环摩擦损失在总转矩损失中的占比很小[11]，因此，可将带轮变形损失近似等效为变速机构在低速空载工况下所需的驱动转矩。

所搭建的试验台如图14所示。驱动电机为7.5 kW的交流变频电机，电机与被测CVT之间装有转矩转速传感器，由于研究对象并不是整台变速箱，CVT中去除了液力变矩器、油泵、离合器总成、减速齿轮总成，带轮的驱动油压及金属带的润滑由外部液压源提供。为了确保主从带轮的夹紧力与计算模型中的夹紧力一致，通过机械限位的方式来固定变速机构的速比，同时通过变速箱液压控制单元来调节主从动油缸的压力。测试工况如下：输入转速分别为100 r/min、200 r/min、300 r/min，金属带速比分别固定在0.44、1.00、2.43，主从动轮压力分别按输入转矩为30 N·m、60 N·m、90 N·m、120 N·m、150 N·m时所需的实际压力施加，测量各个工况下的驱动转矩。试验过程中，油液温度稳定在85～95 ℃范围内。

图14 变速机构空载试验台Fig.14 No-load test bench developed for CVT variator

考虑到试验装置自身传动损失对试验的影响，首先在未安装CVT的条件下测得各转速下空载试验台本身的转矩损失，图15中的测试值是排除试验台自身转矩损失后的测试结果。由图15可知，各转速下的测试结果差别很小，这说明低速条件下输入转速对变形损失基本无影响。实测转矩损失随输入扭矩的增大而增大，速比为0.44和2.43时的损失值大于速比为1时的损失值，这与计算模型中的损失变化规律是一致的。从计算值与测试值的具体对比来看，速比为1时的计算值与测试值吻合较好;速比为0.44和2.43时，计算值比测试值小0.1～0.4 N·m，产生该误差的主要原因是：速比不等于1时，主从动带轮工作半径不相等，金属带各层钢环之间存在相对滑动，该滑动所产生的钢环摩擦损失对测试值造成了一定干扰。总体看来，计算值与测试值的变化趋势一致，钢环摩擦损失造成的误差不影响对整体结果的判断，变形损失模型的可信性得到了验证。

(a)速比i=0.44

(b)速比i=1.00

(c)速比i=2.43图15 计算结果与试验结果对比图Fig.15 Comparison of calculation results and experimental measurements

5 结论

(1)基于所建立的带轮变形损失理论模型，结合某CVT的实际参数，分析得到CVT带轮变形损失变化规律：变形损失随输入转矩的增大而增大，在最小速比和最大速比位置的损失值大于中间速比位置的损失值，楔入损失是构成带轮变形损失的主要部分。

(2)通过变速机构低速空载试验验证了带轮变形损失模型的可信性，该模型可用于CVT变速机构的效率计算及分析。

(3)由带轮变形损失规律可知：带轮包角中心位置的轴向变形是影响变形损失的主要因素，夹紧力一定时，带轮包角中心位置的轴向变形由带轮等效轴向刚度决定，而等效轴向刚度随工作半径的增大而减小。故可通过提升带轮在最大工作半径处的等效轴向刚度来减小带轮变形，从而减小变形损失。研究结果为通过带轮优化设计来提高CVT变速机构的传动效率提供了理论依据。

[1] 程乃士，刘温，郭大忠，等．金属带式无级变速器传动效率的实验研究[J]．东北大学学报(自然科学版)，2000，21(4)：394-396． CHEN Naishi，LIU Wen，GUO Dazhong，et al．Experimental Study of Transmission Efficiency for Metal Pushing V-Belt Type CVT[J]．Journal of Northeastern University (Natural Science)，2000，21(4)：394-396．

[2] 廖建，孙冬野，秦大同．金属带式无级变速器传动效率的理论分析[J]．重庆大学学报(自然科学学报)，2003(3)：12-15． LIAO Jian，SUN Dongye，QIN Datong．Efficiency Analysis of Steel Pushing V-belt Continuously Variable Transmission in Theory[J]．Journal of Chongqing University(Natural Science Edition)，2003(3)：12-15．

[3] AKEHURST S，VAUGHAN N D，PARKER D A，et al．Modeling of Loss Mechanisms in a Pushing Metal V-Belt Continuously Variable Transmission．Part 2：Pulley Deflection Losses and Total Torque Loss Validation[J]．Journal of Automobile Engineering，2004，218(11)：1283-1293．

[4] KIM H，LEE J．Analysis of Belt Behavior and Slip Characteristics for a METAL V-belt CVT[J]．Mechanism and Machine Theory，1994，29(6)：865-876．

[5] MICKLEM J D，LONGMORE D K，BURROWS C R．Belt Torque Loss in a Steel V-belt Continuously Variable Transmission[J]．Proc. Instn. Mech． Engrs.，Part D：Automobile Engineering，1994，208：91-97．

[6] 张晓冰，张友坤，李幼德，等．无级变速器锥轮刚度与楔入损失分析[J]．吉林大学学报(工学版)， 2010，40(3)：614-617． ZHANG Xiaobing，ZHANG Youkun，LI Youde，et al．Analysis of Stiffness and Energy Losses of Push V-belt CVT[J]．Journal of Jilin University (Engineering and Technology Edition) ，2010，40(3)：614-617．

[7] AKEHURST S．An Investigation into the Loss Mechanisms Associated with a Pushing Metal V-belt Continuously Variable Transmission [D]．Bath：the University of Bath,2001．

[8] 程乃士，张伟华，杨会林，等．汽车金属带式无级变速器——CVT原理和设计[M]．北京：机械工业出版社，2004． CHEN Naishi，ZHANG Weihua，YANG Huilin，et al．Metal V-belt Continuously Variable Transmission—Theory and Design[M]．Beijing：China Machine Press，2004．

[9] 曹成龙，周云山，高帅，等．基于滑移率控制的金属带式无级变速器夹紧力研究[J]．中国机械工程，2012，23(12)：2893-2897． CAO Chenglong，ZHOU Yunshan，GAO Shuai，et al．Study on Clamping Force of Metal V-belt Type CVT Based on Slip Control[J]．China Mechanical Engineering，2012，23(12)：2893-2897．

[10] 张飞铁，周云山，薛殿伦，等．无级变速器金属带滑移特性试验研究[J]．机械工程学报，2015，51(2)：90-95． ZHANG Feitie，ZHOU Yunshan，Xue Dianlun，et al．Experiment Research on Slip Characters of Metal V-belt of Continuous Variable Transmission[J]．Journal of Mechanical Engineering，2015，51(2)：90-95．

[11] 张武，刘凯，周春国，等．金属带式无级变速器摩擦功率损失研究[J]．中国机械工程，2010，21(3)：1293-1297． ZHANG Wu，LIU Kai，ZHOU Chunguo，et al．Research on Friction Power Loss of Metal Belt Continuously Variable Transmission[J]．China Mechanical Engineering，2010，21(3)：1293-1297．

(编辑 陈 勇)

Research on Pulley Deflection Losses of Metal Belt CVT

FU Bing1ZHOU Yunshan1GAO Shuai2LI Quan1AN Ying1

1.State Key Laboratory of Advanced Design and Manufacture for Vehicle Body，Hunan University，Changsha，410082 2.Hunan Jianglu & Rundar Vehicle Transmission Co．，Ltd．,Changsha，410205

In order to reduce the transmission loss of CVT，the loss mechanism of pulley deflections was analyzed and a mathematical model of pulley deflection loss calculaton was derived． Based on the pulley deflection model which was established by using finite element method，the radial penetration loss and the wedge loss caused by pulley deflections were quantitatively analyzed，the influence laws of CVT speed ratios and input torques on pulley deflection losses were concluded．The results show pulley deflection losses increase with the increases of input torques，the pulley deflection losses in maximum speed ratio and minimum speed ratio are greater than that in middle speed ratio，the radial penetration loss is the main contributor to pulley deflection losses．The pulley deflection losses may be reduced by increasing pulley equivalent axial stiffnesses in maximum working radius．The calculation model was validated by the experimental data in test bench．

continuously variable transmission (CVT)；pulley deflection；torque loss；transmission efficiency

2016-06-14

国家国际科技合作专项(2014DFA70170)

U463.212

10.3969/j.issn.1004-132X.2017.12.006

傅 兵，男，1987年生。湖南大学机械与运载工程学院博士研究生。主要研究方向为无级变速传动系统、混合动力传动系统。发表论文2篇。E-mail:fubingemail@163.com。周云山，男，1957年生。湖南大学机械与运载工程学院教授、博士研究生导师。高 帅，男，1978年生。湖南江麓容大车辆传动股份有限公司高级工程师、博士。李 泉，男，1976年生。湖南大学机械与运载工程学院博士研究生。安 颖，女，1980年生。湖南大学机械与运载工程学院讲师。