离散缝洞网络油水两相流动的数值模拟

宋世瀚，邸 元，刘中春，代亚非

(1.北京大学 工学院，北京 100871；2.中国石油化工股份有限公司 石油勘探开发研究院，北京 100083； 3. 远景能源(江苏)有限公司，上海 200051)



离散缝洞网络油水两相流动的数值模拟

宋世瀚1，邸 元1，刘中春2，代亚非3

(1.北京大学 工学院，北京 100871；2.中国石油化工股份有限公司 石油勘探开发研究院，北京 100083； 3. 远景能源(江苏)有限公司，上海 200051)

基于溶洞内油水两相流体瞬时平衡和重力分异的假定，采用流相流动分数模拟离散缝洞网络中油水两相的流动，提出一种离散缝洞网络两相流动的数值模拟方法，并编制相应的数值计算程序。分别采用计算流体力学的VOF(volume of fluid)模型和本文中提出的方法对缝洞网络模型算例进行计算，验证了本文方法的正确性。

缝洞型油藏；离散缝洞网络模型；油水两相流；重力分异；流相流动分数

碳酸盐岩油气藏在现今石油天然气工业中具有重要的地位。碳酸盐岩占全球沉积岩面积的20%，相应油气储量约占总储量的50%，而油气产量则约占总产量的60%[1]。碳酸盐岩油气藏中的缝洞型油藏[2]，主要以大型洞穴、溶蚀孔洞和各种裂缝作为储渗空间[3]，表现出极强的非均质性，储层中流体流动状态十分复杂[4-5]。离散缝洞网络模型[6-7]是针对缝洞型油藏非均质性极强的特点而提出的一种数值计算模型，它将储层看作裂缝介质和溶洞介质构成的网络系统，采用Darcy方程模拟裂缝中流体的流动和采用Stokes方程模拟溶洞中流体的流动，并在界面上进行耦合，即Darcy-Stokes耦合计算方法。当表征单元体不存在时，这种模型能准确地对缝洞网络进行模拟[8]。Popov等将网格粗化方法与离散缝洞网络模型相结合，采用Stokes-Brinkmann方程作为控制方程，以避免渗流区和自由流动区在界面上耦合带来的数值困难[9-13]。采用Stokes方程模拟溶洞中的流体流动，现有的离散缝洞网络模型Darcy-Stokes耦合计算方法主要用于单相流体流动问题的数值模拟。Chen等将Cahn-Hilliard公式引入Darcy-Stokes耦合系统，实现了对两相流问题的数值模拟[14-15]，然而这仅限于处理单一界面上的耦合问题，其原因在于，采用该耦合系统模拟缝洞网络各溶洞中的流体流动并计算溶洞内油水两相流的流态时，计算量非常大。因此，Chen等提出的方法目前还难以用于缝洞网络中两相流体流动问题的数值模拟。对溶洞中两相流态的分析表明，在较大的溶蚀孔洞中，毛管力可以忽略，流速低时溶洞内的油水两相应处于重力分异的状态[16]。因此，笔者基于离散缝洞网络模型和溶洞内油水两相流体重力分异的假定，采用流相流动分数描述离散缝洞中油水两相的流动，提出一种离散缝洞网络油水两相流动的计算模型。

1 离散缝洞网络油水两相流动模型

1.1 数学模型

将缝洞型碳酸盐岩储层设定为等温、处于热力学瞬时平衡的状态，并且包含油水两相流体，水和油这两种液体组分仅存在于其伴生相中。油水两组分的物质守恒方程由式(1)和式(2)来描述；β相流体(β为w时代表水，β为o时代表油)在压力、重力和毛管力的作用下，按照式(3)的Darcy定律流动。

(1)

(2)

(3)

Φβ=pβ-ρβgD。

(4)

式(1)～(4)中：φ为储层的有效孔隙度；Sβ为β相的饱和度；ρβ为β相在油藏条件下的密度；vβ为β相的渗流速度；qβ为地层β组分每单位体积汇点/源点项；k为储层的绝对渗透率；krβ为β相的相对渗透率；μβ为β相的黏度；Φβ为β相的流动势；pβ为β相的压力；g为重力加速度；D为深度。

式(1)～(3)、饱和度约束方程和本构方程构成了基本的流动控制方程。

1.2 数值离散

对式(1)和式(2)采用有限体积法进行空间离散，采用向后一阶差分进行时间离散，可得：

(5)

式(5)中：M为β相的质量；n表示前一时刻,n+1表示当前时刻；Vi为单元i的体积；Δt为时间步长；ηi为由所有同单元i相连接的单元j组成的集合；Fβ,ij为单元i同单元j之间β相的质量流动项，计算质量流动项时相对渗透率kr β采用单点上游权处理法；Qβ i为单元i内β相的源/汇项。

式(5)适用于单重或多重连续介质的网格，也适用于离散缝洞网络模型中的裂缝单元或溶洞单元，可通过Newton-Raphson方法进行求解。

2 溶洞单元的流相流动分数

对于离散缝洞网络模型油水两相流动问题，裂缝中的流动可采用Darcy定律来描述；溶洞内部两相流体的流动属于自由流动，是数值计算模型的关键问题。

设定碳酸盐岩缝洞型储层的较大尺度溶洞内油水两相流体瞬时平衡，并处于上油下水的重力分异状态，两相间界面清晰，不存在过渡带且相间毛管力可以忽略。基于此重力分异的假定，可将溶洞单元处理成单一网格，并通过溶洞单元的流相饱和度追踪溶洞中流相界面的变化。

基于重力分异假定计算溶洞内多相流体运动时，式(1)、式(2)及式(5)仍然都成立，式(5)中流动项Fβ,ij可表示为：

Fβ,ij=ρβλβ,ij+1/2γij[Φβ j-Φβ i]。

(6)

式(6)中：λβ,ij+1/2为β相的流度；γij为单元i和单元j交界面处的传导系数。

(7)

(8)

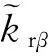
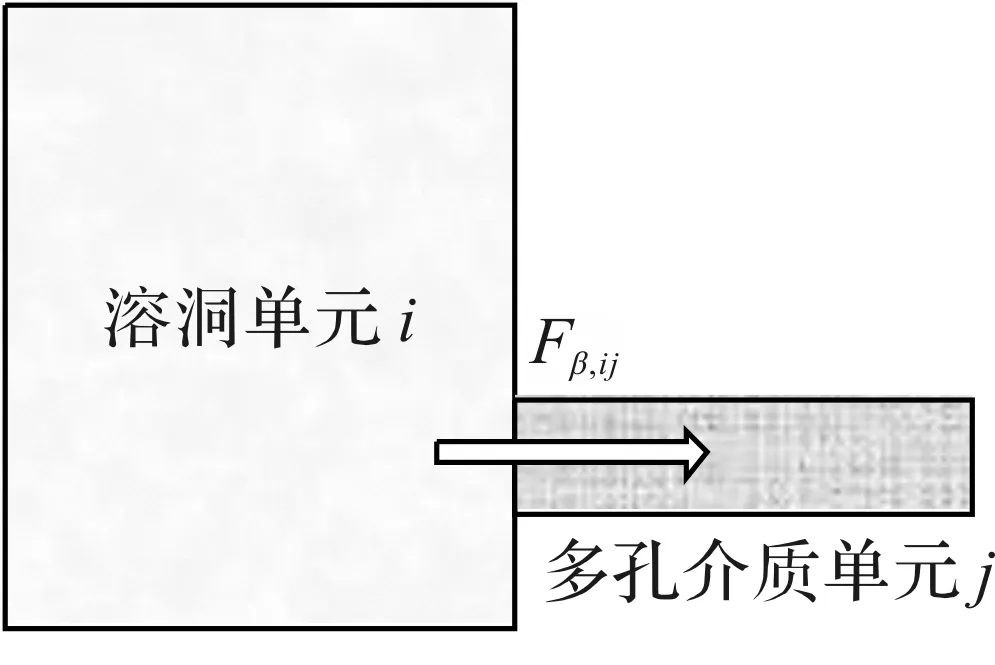
图1 流相流动分数取值的示意Fig.1 Schematic of flow fraction

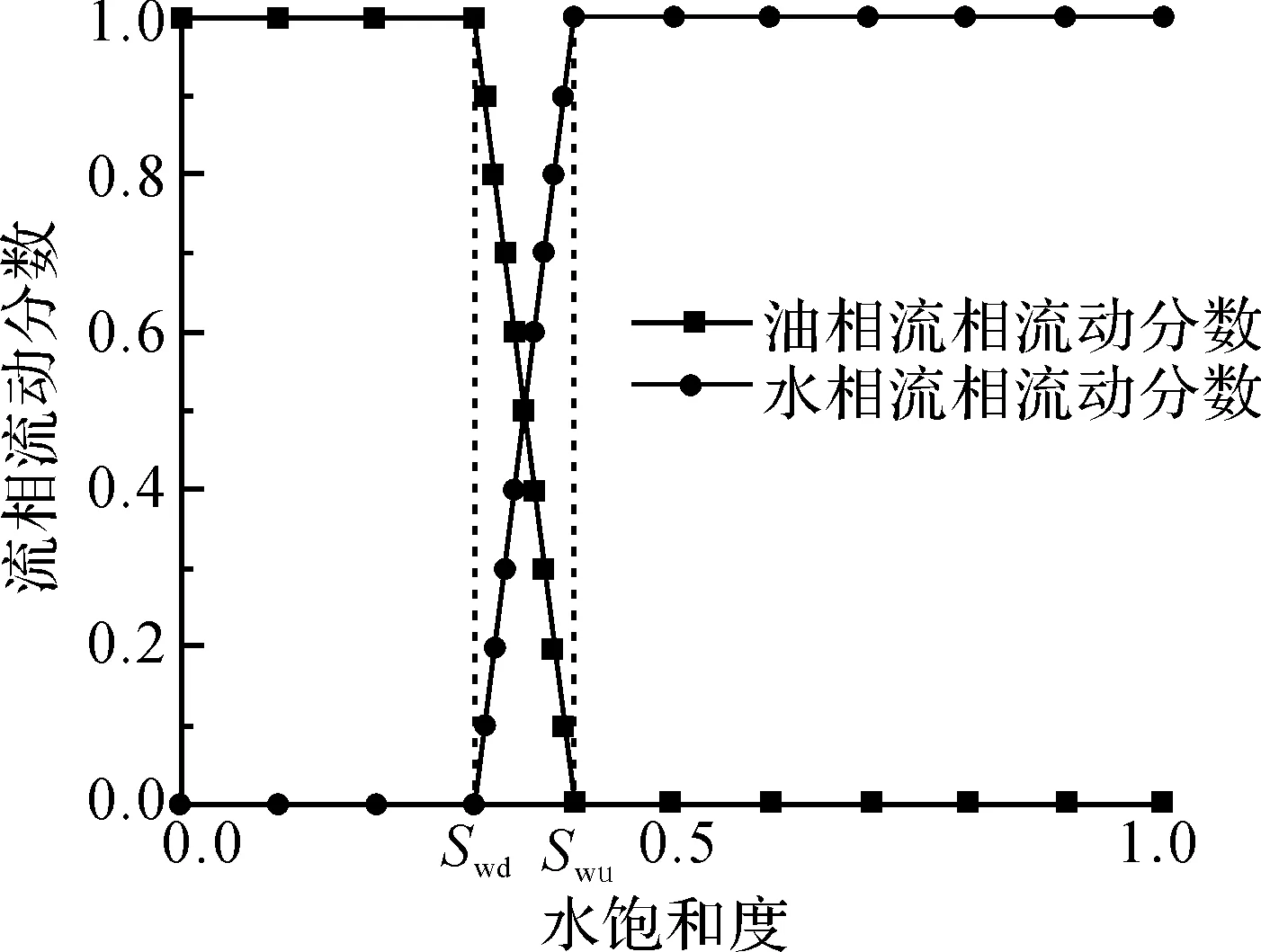
图2 单元i到单元j的流相流动分数Fig.2 Flow fraction of the connection from element i to j

3 算例分析

3.1 验证算例

假设一个双洞串联缝注缝采模型算例，两个矩形溶洞的尺寸相同，由一裂缝相连，左侧溶洞由裂缝连接到注入井，右侧溶洞由裂缝连接到生产井。初始时刻模型油相饱和，注入井以恒定速率0.144 m3/d注水。

分别采用3种方法对此算例进行模拟计算。第一种是传统的基于连续介质的数值模拟方法，即将溶洞划分成细密的网格，并赋予超大的渗透率；第二种是采用计算流体力学的VOF(volume of fluid)两相流动模型进行计算；第三种是本文基于重力分异假定、采用流相流动分数控制的计算方法。采用第一种和第二种计算方法模拟时，使用结构化的正方形网格对研究区域进行剖分，单元总数为19 440个。

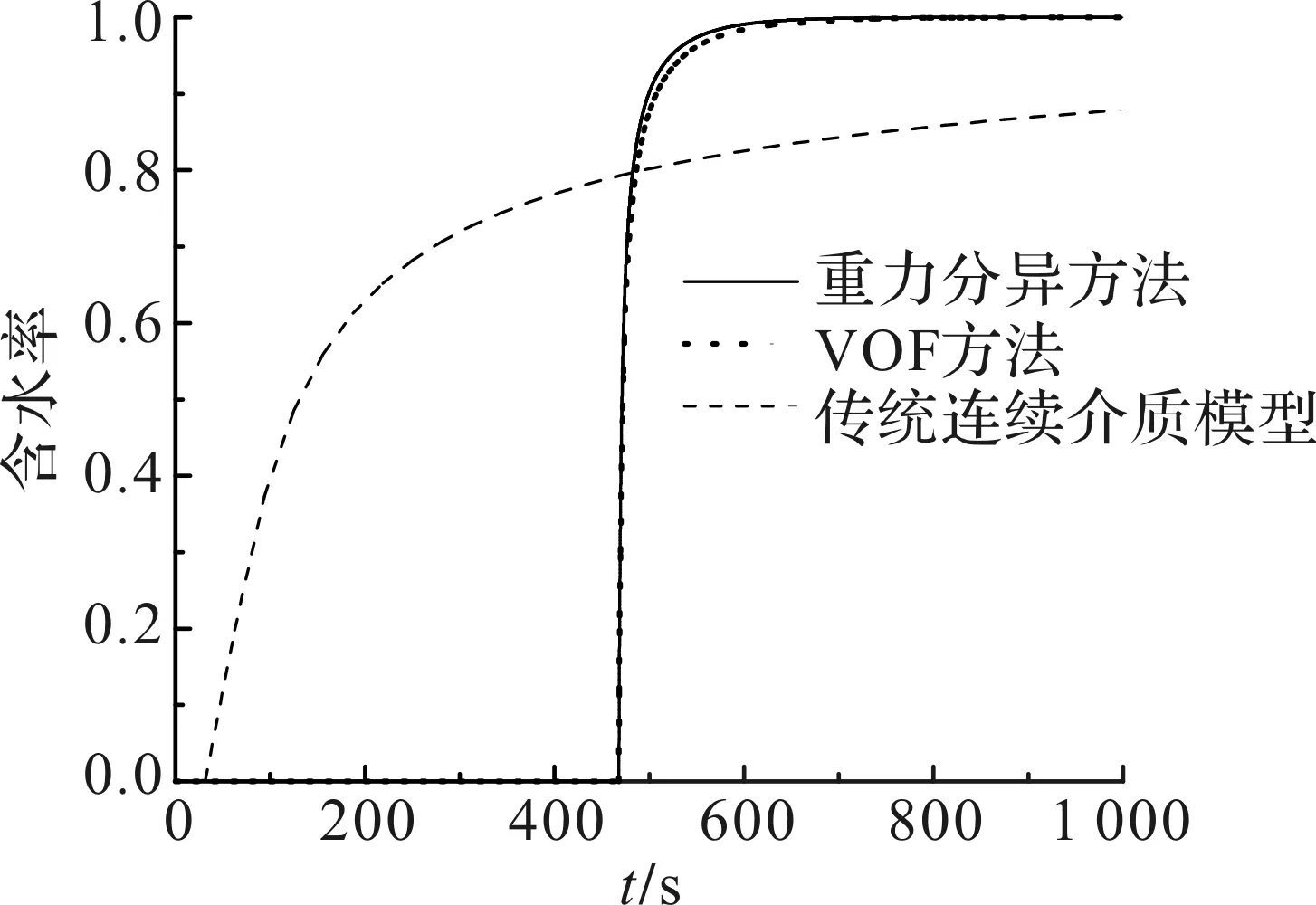
图3 双洞串联缝注缝采模型算例的含水率曲线Fig.3 Water-cut curve of dual-vug model

图3给出了3种不同计算方法对应的生产井含水率随时间的变化曲线。图4为由VOF油水两相流模型和传统基于连续介质渗流的数值模拟方法计算得到的同一时刻的油相饱和度分布图(t=0.048 h)，此时右侧溶洞见水。计算结果表明，离散缝洞网络两相流动模型的计算结果与VOF油水两相流模型的计算结果基本一致，由此验证了该方法和模拟程序的正确性。传统基于连续介质的数值模拟方法不能反映油水两相在溶洞内流动时重力引起的分异作用，无水采油期很短。VOF方法虽然能够准确地反映大溶洞中油水界面的变化，但是使用的网格数量较大，计算耗时较长，难以处理溶洞数量较多的算例。本文提出的计算方法只需用2个网格即可准确模拟生产井含水率，以及采出程度的变化特征，这大大降低了计算量，因而计算效率较高。

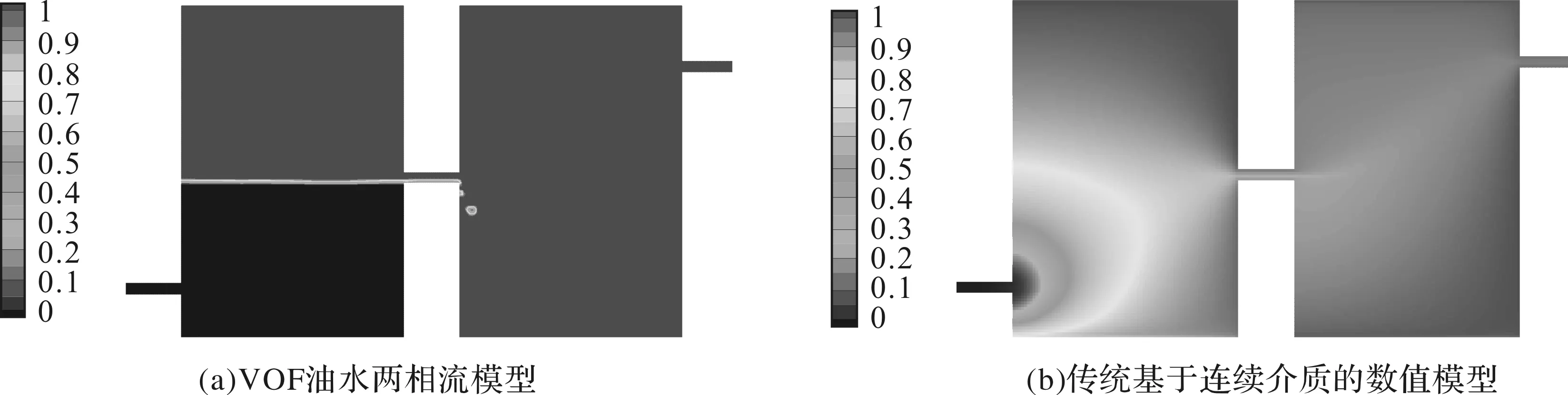
图4 油相饱和度分布Fig.4 Distribution of oil saturation

3.2 缝洞网络模型算例

假设如图5所示的缝洞网络的油水两相流动问题，忽略基质储渗能力。模型初始为油相饱和，水从下部溶洞1定流量注入，每天的注水量为溶洞总体积的千分之一，从上部溶洞7定压采出。

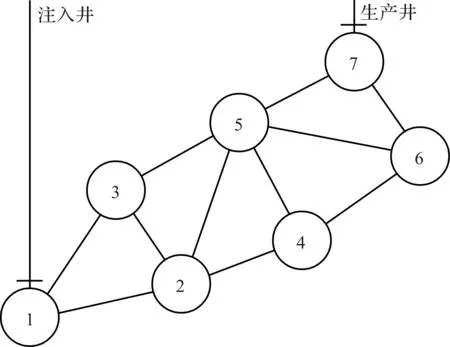
图5 缝洞网络模型算例示意Fig.5 Schematic of a fracture-vug network model

采用本文提出的方法对该缝洞网络模型算例进行数值模拟。图6给出了计算而得的生产井含水率曲线和日采油率曲线。计算结果表明，与双洞串联缝注缝采模型算例一样，缝洞网络模型算例中同样出现了无水采油期后生产井含水率短时间内迅速上升到1.0的情况。这种暴性水淹现象在实际缝洞型油藏的开采过程中也较为常见[17]。

模拟结束时(约1 500 d)各溶洞内水相饱和度如表1所示。表1中还给出了各溶洞流体流出方向的连接中水相流动分数为1.0时水相饱和度的最小值，同图5缝洞网络几何构形相对比，各溶洞内水相饱和度完全满足预先设定的溶洞内油水两相重力分异的假定。

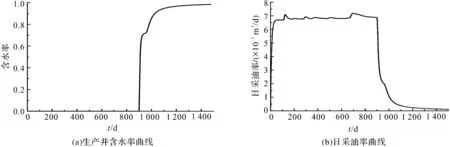
图6 缝洞网络模型算例模拟结果Fig.6 Numerical result of the fracture-vug network model

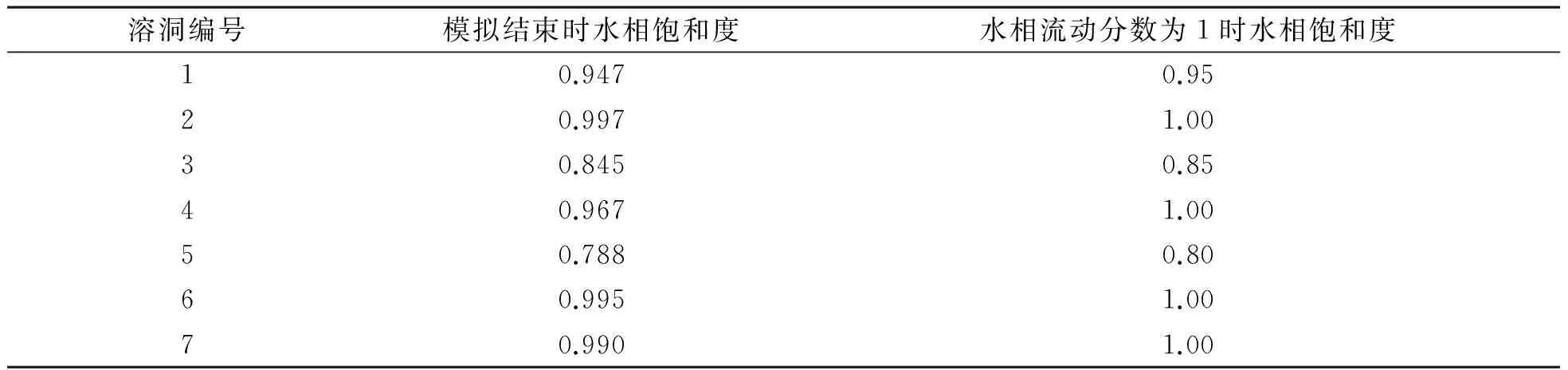
溶洞编号模拟结束时水相饱和度水相流动分数为1时水相饱和度10.9470.9520.9971.0030.8450.8540.9671.0050.7880.8060.9951.0070.9901.00

计算结果也表明，在模拟结束时各裂缝内仅有水相流动，溶洞内油相体积几乎不再变化，剩余油均为无法被采出的阁楼油，这同文献[18]由实验得到的结论相吻合。当生产井见水后，由于裂缝尺度相比溶洞尺度小几个数量级，生产井与溶洞的连接内水相流动分数会很快随着溶洞水相饱和度的微小增加而迅速接近或达到1.0，因此生产井出现了明显的暴性水淹现象。

4 结 论

笔者基于溶洞内油水两相流体瞬时平衡和重力分异的假定，提出了一种离散缝洞网络两相流动的数值模拟方法，采用流相流动分数来模拟离散缝洞网络中油水两相的流动，并编制相应的数值计算程序。分别采用了传统基于连续介质的数值模拟方法(对溶洞细分网格并设定超大渗透率)、计算流体力学的VOF两相流动模型和本文建议的算法，对一个双洞串联缝注缝采模型算例进行了计算。结果表明，传统基于连续介质的数值模拟方法不能很好地模拟缝洞网络的流体流动特征，无水采油期很短。本文离散缝洞网络两相流动模型的计算结果与VOF油水两相流模型的计算结果基本一致，且只需用两个网格即可准确模拟采出井含水率及采出程度的变化特征，这大大降低了计算量。对缝洞网络模型算例的计算结果表明，各溶洞中水饱和度的分布符合缝洞分布的几何构形，完全满足预先设定的溶洞内油水两相重力分异的假定；无水采油期后，生产井含水率短时间内迅速上升，出现了明显的暴性水淹现象。

[1] 江怀友，宋新民，王元基，等.世界海相碳酸盐岩油气勘探开发现状与展望[J].海洋石油,2008,28(4):7.

[2] 林忠民.塔河油田奥陶系碳酸盐岩储层特征及成藏条件[J].石油学报,2002,23(3):23.

[3] 李江龙，陈志海，高树生.缝洞型碳酸盐岩油藏水驱油微观实验模拟研究：以塔河油田为例[J].石油实验地质,2009,31(6):637.

[4] 康志江，李江龙，张冬丽，等.塔河缝洞型碳酸盐岩油藏渗流特征[J].石油与天然气地质,2005,26(5):640.

[5] 李超，李龙龙，汪洋，等.复杂裂缝性碳酸盐岩油藏数值模拟方法研究[J].长江大学学报(自然科学版),2015,12(20):65.

[6] ARBOGAST T, BRUNSON D S. A computational method for approximating a Darcy-Stokes system governing a vuggy porous medium[J]. Computational Geosciences, 2007, 11(3):207.

[7] 姚军，黄朝琴，王子胜，等.缝洞型油藏的离散缝洞网络流动数学模型[J].石油学报,2010,31(5):815.

[8] BERKOWITZ B. Characterizing flow and transport in fractured geological media: a review[J]. Advances in Water Resources, 2002, 25(8):869.

[9] POPOV P, QIN G, BI L, et al. Multiphysics and multiscale methods for modeling fluid flow through naturally fractured carbonate karst reservoirs[J]. SPE Reservoir Evaluation and Engineering, 2009, 12(2): 218.

[10] POPOV P, EFENDIEV Y, QIN G. Multiscale modeling and simulations of flows in naturally fractured karst reservoirs[J]. Communications in Computational Physics, 2009, 6(1):162.

[11] GULBRANSEN A, HAUGE V L, LIE K A. A multiscale mixed finite element method for vuggy and naturally fractured reservoirs[J]. SPE Journal, 2009, 15(15):395.

[12] HE J, KILLOUGH J E, FADLElMULA F, et al. A unified finite difference model for the simulation of transient flow in naturally fractured carbonate karst reservoirs[C]//SPE Reservoir Simulation Symposium. Houston, Texas: Society of Petroleum Engineers, 2015.

[13] HE J, KILLOUGH J E, GAO S, et al. Confronting the simulation of fluid flow in naturally fractured carbonate karst reservoirs[C]//Abu Dhabi International Petroleum Exhibition and Conference. Abu Dhabi: Society of Petroleum Engineers, 2016.

[14] CHEN J, SUN S, WANG X P. A numerical method for a model of two-phase flow in a coupled free flow and porous media system[J]. Journal of Computational Physics, 2014, 268(2):1.

[15] XIE H, LI A, HUANG Z, et al. Coupling of two-phase flow in fractured-vuggy reservoir with filling medium[J]. Open Physics, 2017, 15(1):12.

[16] 代亚非.缝洞型碳酸盐岩油藏数值模拟[D].北京:北京大学,2014.

[17] 李小波，荣元帅，龙喜彬，等.缝洞型油藏强边、底水窜进油井特征及机理研究[J].西南石油大学学报(自然科学版),2015,37(1):136.

[18] 刘中春.塔河缝洞型油藏剩余油分析与提高采收率途径[J].大庆石油地质与开发,2015,34(2):62.

Numerical simulation of oil-water two-phase flow
in the discrete fracture-vug network

SONG Shihan1, DI Yuan1, LIU Zhongchun2, DAI Yafei3

(1. College of Engineering, Peking University, Beijing 100871, China; 2. Exploration and Production Research Institute, China Petroleum and Chemical Corporation, Beijing 100083, China; 3. Envision Energy Limited, Shanghai 200051, China)

Based on the assumption of transient equilibrium and gravity segregation of oil-water two-phase flow in major vugs, a numerical method is proposed to simulate the two-phase flow in the discrete fracture-vug network by using flow fraction, with the corresponding numerical calculation program developed. Several numerical examples of the fracture-vug network are calculated by applying the model of volume of fluid(VOF) and the proposed method of the article respectively, whose numerical results have proved validity of the proposed method.

fractured-vuggy reservoir; discrete fracture-vug network model; oil-water two-phase flow; gravity segregation; flow fraction

10.3969/j.issn.1671-8798.2017.03.003

2017-04-02

国家科技重大专项项目(2016ZX05014)；国家自然科学基金项目(51674010)

邸 元(1968— )，男，陕西省西安人，副教授，博士，主要从事油藏数值模拟研究。E-mail：diyuan@mech.pku.edu.cn。

TE344；O359

A

1671-8798(2017)03-0172-06