双曲正弦平方高斯光束通过EIT介质的传输特性

许森东

(浙江科技学院 理学院，杭州 310023)



双曲正弦平方高斯光束通过EIT介质的传输特性

许森东

(浙江科技学院 理学院，杭州 310023)

为了研究双曲正弦平方高斯光束通过四能级EIT介质的传输特性，利用广义惠更斯-菲涅耳衍射积分公式推导双曲正弦平方高斯光束通过四能级EIT介质的传输解析公式，并利用该公式分析双曲正弦平方高斯光束通过四能级EIT介质的传输特性。研究发现，通过改变偏心参数或者四能级EIT介质控制光的拉比频率就可以实现对不同传输位置的光束进行整形，同时发现了一种调控双曲正弦平方高斯光束光强的新方法。

双曲正弦平方高斯光束;光强;惠更斯-菲涅耳衍射积分;拉比频率

电磁感应透明(electromagnetic induced transparency, EIT)是一种可以消除介质对电磁辐射传输影响的技术。电磁感应透明是由于量子相干产生的奇特效应，已经证明EIT 的光学性质可以通过外部条件来控制。EIT介质具有很多常规介质所不能获得的奇特效应和应用，近年来科研人员持续对其进行过基础及应用研究[1-4]。此外，唐宏等研究了纵波光学声子耦合对EIT半导体量子阱中光孤子的调控[5]；杜英杰等研究了EIT的高阶非线性效应对光孤子的影响[6]；巴诺等研究了一维原子晶格中基于EIT的可控光子带隙[7]；许森东等研究了Airy光束在EIT介质中的传输特性[8]；庄飞等研究了利用EIT介质实现可控光子晶体带隙结构[9]。随着激光技术的不断发展，激光光束在科学研究和实际生活中的应用越来越广泛。其中，激光光束的传输变换研究对人们控制和应用激光光束具有十分重要的作用。双曲正弦平方高斯光束(sinh-squared-Gaussian beams, ShSGB)作为一种典型的厄米-正弦类高斯光束[10-11]，其传输特性受到科研人员的广泛关注，如龚霞等研究了ShSGB光束通过左手平板材料的传输特性，发现负折射率会影响光束的传输特性[12]；李艳桃等研究了ShSGB光束在单轴晶体中垂直于光轴的传输特性[13]；王喜庆研究了ShSGB光束的聚焦特性[14]。但到目前为止，还没有人对ShSGB光束通过EIT介质的传输特性进行过研究。EIT介质的独特性质使得光束通过EIT介质能获得奇特的传输特性。因此，研究ShSGB光束通过EIT介质的传输特性是有意义的，笔者从ShSGB光束的原理出发来研究ShSGB光束通过EIT介质的传输特性。

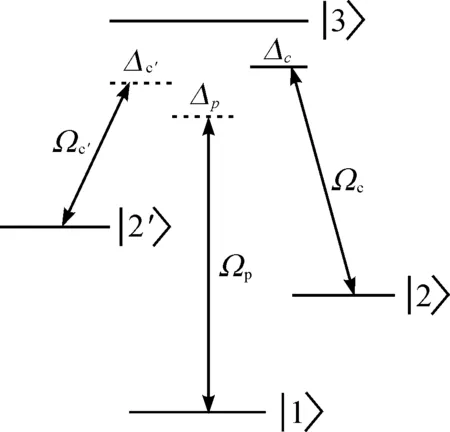
图1 四能级原子系统示意图Fig.1 Schematic diagram of four-level atomic system

1 四能级EIT介质

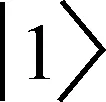
(1)

式(1)中：N为介质的原子数密度；βe为原子电极化率。

(2)

(3)

式(3)中：Γ3为跃迁的辐射衰变率；Ωc、Ωc′分别为控制光拉比频率。

2 双曲正弦平方高斯光束通过EIT的传输特性

双曲正弦平方高斯光束在z=0初始平面上的场分布为：

(4)

式(4)中：ω0为双曲正弦平方高斯光束的束腰宽度；Ω0为双曲正弦平方高斯光束双曲正弦平方相关参数值。

在傍轴近似下，利用广义惠更斯-菲涅耳衍射积分公式可得，当双曲正弦平方高斯光束通过EIT介质后的出射面上的场分布：

(5)

利用三角函数公式，将式(4)改写为：

(6)

利用特殊积分式：

(7)

和

(8)

将式(6)代入式(5)，利用式(7)～(8)，可以得到双曲正弦平方高斯光束通过ABCD光学系统的传输公式：

(9)

双曲正弦平方高斯光束通过EIT介质的传输矩阵可表示为：

(10)

将式(10)代入式(9)，经整理可得：

(11)

此时，双曲正弦平方高斯光束的光强I为：

I(x′,y′,z)=E(x′,y′,z)E*(x′,y′,z)。

(12)

令α=Ω0ω0，α为偏心参数。将式(11)代入式(12)即可得到双曲正弦平方高斯光束通过EIT介质的光强分布，轴上光强分布则为：

(13)

3 计算结果与分析

式(13)即为双曲正弦平方高斯光束通过EIT介质的传输公式， 通过计算即可得到双曲正弦平方高斯光束通过EIT介质的传输特性。双曲正弦平方高斯光束通过EIT介质后的光强分布情况与EIT介质的相关参数、束腰宽度ω0、偏心参数α等有关。EIT介质参数选取如下值：D13=1.2×10-29C·m,频率失谐Δp=2.5×107s-1，Δc=2.0×107s-1，Δc′=1.0×107s-1，拉比频率Ωc=0.5Ωc′，相干失相速率γ2=105s-1，γ2′=2×105s-1，辐射衰变率Γ3=2×107s-1。双曲正弦平方高斯光束相关参数选取：λ=1.06×10-3mm，ω0=3.001×10-5mm。其他参数为：ћ=1.05×10-34J·s，ε0=8.85×10-12F/m。

图2为偏心参数α取不同值时双曲正弦平方高斯光束通过EIT介质传输时轴上归一化光强I/Imax随z的变化曲线图。参数选取：Ωc=1.4×108Hz，α1=2,α2=3,α3=4。分析图2可知，双曲正弦平方高斯光束通过EIT介质传输时，轴上光强会出现一个极大值。极大值出现在轴上的位置会随着偏心参数α取值发生变化，偏心参数α越大，光强极大值的位置距离光源越远。另外，轴上光强随z的变化一开始是逐渐增大，到出现极大值后又逐渐减小。

图3为拉比频率Ωc取不同值时双曲正弦平方高斯光束通过EIT介质传输时轴上归一化光强I/Imax随z的变化曲线图。参数选取：α1=2，Ωc1=6×107Hz，Ωc2=10×107Hz，Ωc3=14×107Hz。分析图3可知，双曲正弦平方高斯光束通过EIT介质传输时，轴上光强会出现一个极大值，且极大值出现在轴上的位置会随着拉比频率Ωc取值发生变化。另外，轴上光强随z的变化一开始是逐渐增大，到出现极大值后又逐渐减小。

图2 偏心参数α取不同值时轴上归一化光强随z的变化Fig.2 Axial normalized intensity distributions change with propagation distances at different decentered parameters

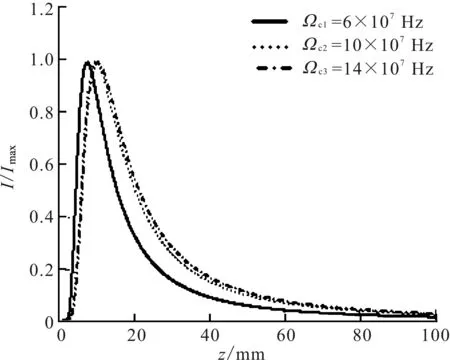
图3 拉比频率取不同值时轴上归一化光强随z的变化Fig.3 Axial normalized intensity distributions changes with propagation distance for different Rabi frequency

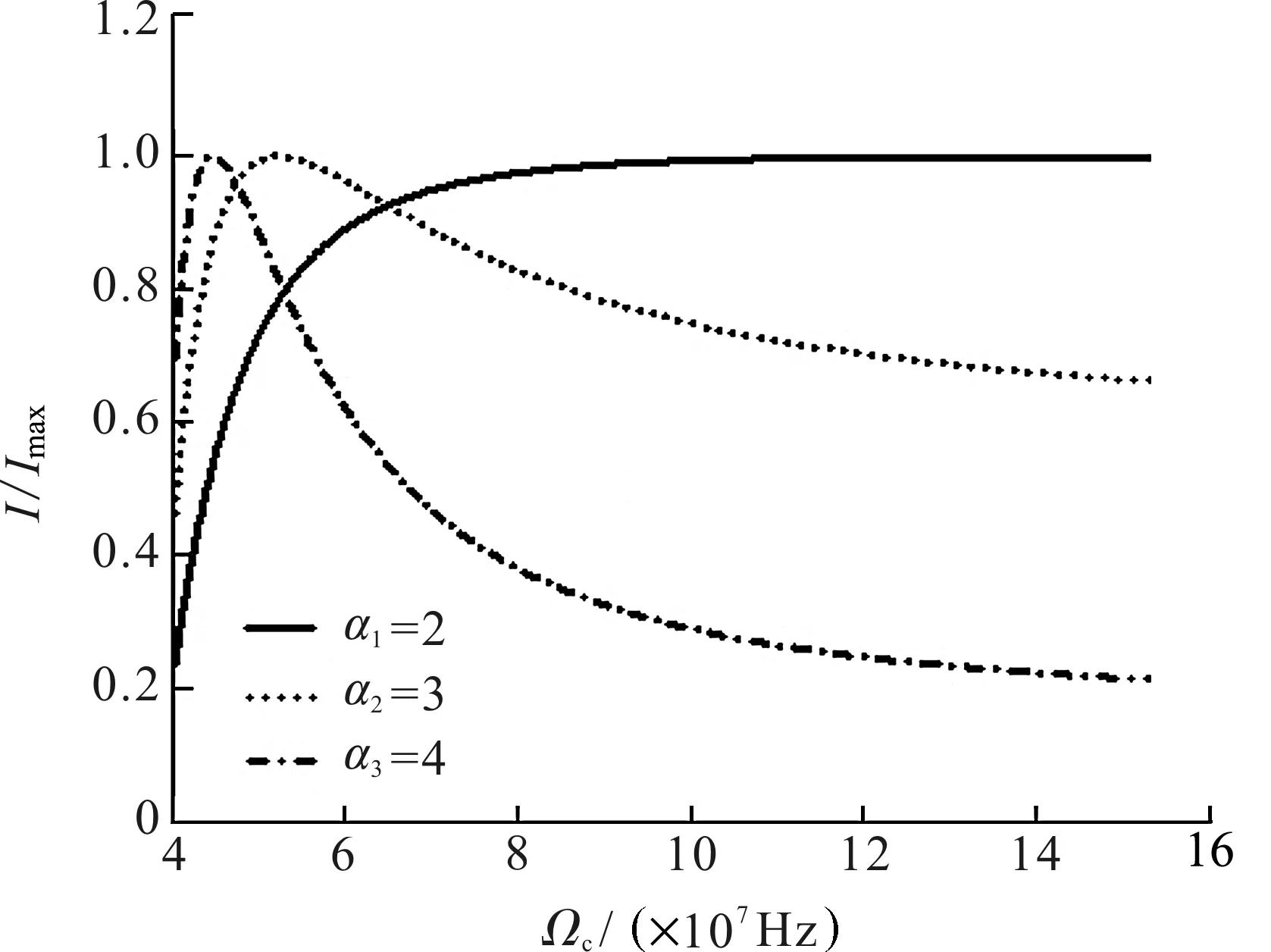
图4 偏心参数α取不同值时轴上归一化光强随Ωc的变化曲线Fig.4 Axial normalized intensity distributions change with Rabi frequency at different decentered parameters

图4为偏心参数α取不同值时双曲正弦平方高斯光束通过EIT介质传输时轴上归一化光强I/Imax随Ωc的变化曲线图。参数选取：z=10 mm，α1=2，α2=3，α3=4。从图4中可以看出，同一位置z=10 mm轴上光强可由EIT介质的控制光拉比频率所调控。当光束的其他参数选定相同值时，改变EIT介质的控制光拉比频率就可以实现对光强的控制。另外，若偏心参数α取值不同，同一位置z=10 mm轴上光强也不同。当偏心参数α取某些值时，光强会随着拉比频率的增大而出现一个拐点，且拐点的位置随偏心参数α变化。

4 结 论

笔者推导出了双曲正弦平方高斯光束通过四能级EIT介质的传输光强解析公式，并利用该解析公式研究了双曲正弦平方高斯光束通过四能级EIT介质的传输特性。研究发现，双曲正弦平方高斯光束通过四能级EIT介质传输时，轴上光强会出现唯一的一个极大值，且极大值的位置随偏心参数α取值的不同而改变。研究还发现，可以通过调控四能级EIT介质控制光的拉比频率来控制光强。这些发现显示，通过改变偏心参数α或者四能级EIT介质控制光的拉比频率就可以实现对不同传输位置的光束进行整形，这是一种通过调控四能级EIT介质控制光实现对光强控制的新方法。

[1] 杨智伟,焦月春,韩小萱,等.调制激光场中Rydberg原子的电磁感应透明[J].物理学报,2016,65(10):103201-1.

[2] 杜英杰,杨战营,白晋涛,等.电磁感应透明介质的高阶非线性特性[J].光学学报,2014,34(6):0627001-1.

[3] 佘彦超,张蔚曦,王登龙.电磁感应透明介质中非线性法拉第偏转[J].物理学报,2011,60(6):064205-1.

[4] 赵虎,李铁夫,刘建设,等.基于超导量子比特的电磁感应透明研究进展[J].物理学报,2012,61(15):154214-1.

[5] 唐宏,王登龙,张蔚曦,等.纵波光学声子耦合对级联型电磁感应透明半导体量子阱中暗-亮光孤子类型的调控[J].物理学报,2017,66(3):034202-1.

[6] 杜英杰,杨战营,谢小涛,等.电磁感应透明的高阶非线性效应对光孤子的影响[J].光学学报,2015,35(2):0227002-1.

[7] 巴诺,王磊,吴向尧,等.一维原子晶格中基于电磁感应透明的可调控光子带隙[J].光子学报,2015,44(6):0627002-1.

[8] 许森东,徐弼军.Airy光束在A型三能级EIT介质中的传输特性研究[J].量子电子学报,2013,30(5):554.

[9] 庄飞,沈建其,叶军.调控电磁感应透明气体折射率实现可控光子带隙结构[J].物理学报,2007,56(1):541.

[10] 黄永超,张廷蓉.复变量双曲正弦高斯光束在左手材料中的传输[J].光学与光电技术,2015,13(4):75.

[11] 朱开成,朱正和,唐慧琴.双曲余弦平方-高斯光束的传输特性研究[J].激光技术,2002,26(3):192.

[12] 龚霞,张廷蓉,杨玉婷,等.双曲正弦平方高斯光束通过左手平板材料的传输特性[J].中国激光,2016,43(6):0605001-1.

[13] 李艳桃,张廷蓉,张伟林,等.双曲正弦平方-高斯光束在单轴晶体中垂直于光轴的传输[J].激光与光电子学进展,2012,49(6):062601-1.

[14] 王喜庆.双曲正弦平方-高斯光束的聚焦特性[J].学术动态,2006(1):27.

[15] ZHUANG F, SHEN J, DU X,et al.Propagation and modulation of Airy beams through a four-level electromagnetic induced transparency atomic vapor[J].Optics Letters,2012,37(15):3055.

Study on propagation properties of sinh-squared-Gaussian beams through an electromagnetically induced transparency medium

XU Sendong

(School of Sciences, Zhejiang University of Science and Technology, Hangzhou 310023, Zhejiang, China)

In order to explore the propagation properties of sinh-squared-Gaussian beams(ShSGB) through a four-level electromagnetically induced transparency(EIT) medium, the article deduces the analytical formula of ShSGB passing through the four-level EIT medium, based on the generalized Huygens-Fresnel diffraction integral theory. Furthermore, the intensity of the beams through the four-level EIT medium is obtained by using the formula. The results show that it is feasible to shape beams in the manner of adjusting the decentered parameter or Rabi frequency of the four-level EIT medium at different propagation positions, with a new method of modulating the ShSGB intensity being discovered.

sinh-squared-Gaussian beams; intensity; Huygens-Fresnel diffraction integral; Rabi frequency

10.3969/j.issn.1671-8798.2017.03.001

2017-03-29

浙江省教育厅科研计划项目(Y201533236)

许森东(1981— )，男，重庆市大足人，高级实验师，硕士，主要从事人工复合电磁介质研究。E-mail:xusendong@163.com。

O43

A

1671-8798(2017)03-0161-05