圆轨道航天器在轨加注任务空间燃料站部署问题

朱啸宇，乔兵,*，张庆展，靳永强，谭迎龙

1.南京航空航天大学 航天学院，南京 210016 2.上海宇航系统工程研究所，上海 201109



圆轨道航天器在轨加注任务空间燃料站部署问题

朱啸宇1，乔兵1,*，张庆展2，靳永强2，谭迎龙1

1.南京航空航天大学 航天学院，南京 210016 2.上海宇航系统工程研究所，上海 201109

在轨服务技术因在航天器故障修复、寿命延长及军事方面有重大辅助作用而越来越受到各航天大国的重视，作为在轨服务技术重要组成部分的在轨燃料补给技术也越来越受到关注。文章针对圆轨道航天器在轨燃料加注任务，将空间燃料站技术与多目标在轨加注技术相结合，对基于燃料站的在轨加注模式进行了研究，提出了一种基于聚类分析的在轨加注任务调度及优化算法。通过对双脉冲轨道转移问题的求解与分析，获得了轨道转移速度增量和轨道参数之间的关系，在此基础上分析了圆轨道航天器在轨加注任务调度问题，并根据调度模型的变量和约束关系，建立了圆轨道航天器在轨加注任务多目标规划模型，并采用免疫遗传算法对加注任务调度空间燃料站选址问题进行了研究。以30颗目标航天器的在轨加注任务为例进行了数值仿真，并由燃料消耗的计算结果验证了算法的有效性。

圆轨道航天器；在轨加注；任务调度；多目标规划；聚类算法；空间燃料站

随着空间交会对接技术的不断成熟，航天器在轨服务技术已经成为航天器在轨故障修复、寿命延长及太空军事对抗的重要手段，在轨燃料补给(以下简称在轨加注)作为在轨服务的重要形式之一，近年来已成为航天科技领域的研究热点，随着科技的不断进步，在轨加注将成为世界航天事业可持续发展的重要保障技术，因而备受关注。

早在20世纪90年代，东京大学就已经提出了建立“基于未来空间站的太空交通运输网”的设想[1-2]，文中指出，在针对未来GEO轨道、地月轨道、行星际轨道等的高能耗、周期长的航天任务时，利用轨道转移飞行器(Orbital Transfer Vehicles，OTV)与空间站，模拟地面运输系统，构建太空运输网，将极大地提高该类任务的经济效益。而卫星星座组网是该设想的研究基础，文献[3-4]阐述了星座部署优化设计的思路，优化目的是使每次发射后星座性能得到最大限度的提升，比较了分别采用启发式进化优化算法和穷举法进行星座部署的区别，指出了对于常见的星座构型，用穷举法进行部署优化的效率较高。

针对卫星星座燃料补给的任务需求，国内外也越来越多地将研究重点投入到多目标在轨加注方式。分析研究表明多目标航天器加注方式较传统加注方式具有更好的效费比，将成为未来在轨加注的主流方式[5]。多目标航天器在轨加注调度的目的是找到总燃耗最小的最优加注服务顺序及最佳时间分配方案，研究表明，最优服务顺序总是在一些总扫描角最小的序列中[6]。在文献[6]的基础上，文献[5]对比分析了单航天器加注、P2P(Peer-to-Peer)加注和混合P2P加注三种不同在轨加注服务模式的调度问题，结果表明混合P2P加注策略能够让燃料的整体消耗更出色。文献[8-9]则延续了文献[7]的研究，提出了一种异步最优混合P2P在轨加注调度策略，显著地减少了P2P加注方案轨道机动的成本。文献[10-11]对基于伴飞模式的星与星座间燃料补给问题进行了研究，结果表明服务航天器的燃料利用率与用于轨道转移的燃料消耗量及转移给目标航天器的燃料转移量有关，合理地规划服务航天器的轨道可以有效地提高燃料利用率，但是对于服务航天器所带的燃料限制及目标航天器加注需求不同的情况未进行考虑。文献[12]全面系统地阐述了交会对接任务规划的问题建模、求解理论、算法模型和规划软件等内容，对于实际航天任务设计起到了理论指导作用。

文献[13]考虑了实际工程中轨道倾角对在轨加注任务调度的影响，并以GEO卫星群为研究对象，研究了多服务卫星下的多目标规划问题。但是考虑到卫星发射所带来的经济效益，可以在空间中利用已有空间站或者设立新空间燃料站，使服务航天器在执行任务的过程中，自身燃料也能及时得到补给。

本文针对圆轨道航天器，考虑服务航天器自身携带的推进剂限制，在传统“服务航天器-目标航天器”的二层轨道模式基础上，将空间燃料站作为服务航天器执行在轨加注的中转站，开展基于空间燃料站的圆轨道航天器在轨加注任务调度问题的研究。

1 数学模型

1.1 任务场景及规划问题

1992年首次提出在空间中建立燃料站形成“太空交通运输网”这一构架的设想，由于过去的在轨加注或服务任务大都由地面发射卫星完成，这一设想的研究仅仅停留在经济可行性分析阶段。基于燃料站的圆轨道航天器在轨加注进行任务调度及优化，如图1所示，在目标航天器轨道(Orbit-3)上有N个目标航天器软硬件运行正常，面临燃料枯竭问题，需要通过在轨燃料加注来延长在轨寿命。K个服务航天器SSc和M个燃料站FS分别部署在轨道Orbit-1和Orbit-2上。

服务航天器在给定时间内，从初始轨道出发，首先通过变轨与燃料站进行交会对接，从燃料站获取燃料后与燃料站分离，之后服务航天器携带燃料进行轨道机动，按照经过优化后的加注顺序依次对目标航天器进行加注，在加注完一个目标航天器后，当服务航天器携带的燃料不足以完成下一个目标航天器的加注时，需返回到燃料站，再次与燃料站交会对接补充燃料，继而进行后续的加注作业。简而言之，这是一种支持服务航天器针对多目标加注任务时需多次往返的调度策略，在传统调度模型的基础上，提高了任务的灵活性与应急能力。

服务航天器在补加完全部目标航天器后，返回初始轨道前需检查自身剩余的燃料量，当燃料充足时直接返回到初始轨道，燃料不足时先返回到燃料站轨道补充燃料后，再返回到初始轨道。

从任务场景的描述可以看出，若将每个服务航天器的任务单独提炼出来，可以将其视作单服务航天器的在轨加注任务模型。本文把聚类算法用于该网络下的太空燃料站选址问题中，在一定的约束条件下，建立该部署问题的数学模型，并采用聚类算法求解较为合理的燃料站部署位置。

1.2 优化模型

(1)

则服务航天器携带燃料从空间燃料站tj出发机动至目标航天器si的速度增量为：

(2)

服务航天器的发动机比冲记为Isp，服务航天器的质量为M0，各目标航天器所需要补给的燃料质量为MS={mS1,mS2,…,mSi,…,mSn}，服务航天器从空间燃料站变轨至目标位置所需要的燃料表示为：

(3)

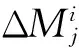
该模型可以等效为一个地面运输中的选址/分配模型，在满足燃料消耗最优的条件下，需要为n个目标航天器序选择合适的位置设立空间燃料站，并通过服务航天器向各个目标航天器供给燃料。在太空交通运输网的运作中，服务航天器的任务就是根据各个卫星的需求及时、准确和经济地将补给或元件运送至目标。而该模型中，空间燃料站作为在轨加油任务的中转站，其轨道参数往往决定着在轨加注任务的燃耗和服务模式，进而影响着整个系统的运作效率，基于以上条件，此非线性规划模型的目标函数可以表示为：

(4)

目标函数可以改写为：

(5)

约束条件：

(6)

当任务时间较长时，共面轨道转移产生的速度增量，在该小倾角的近似计算中属于次要优化目标，但仍需通过其确定空间燃料站的经度分布。可以证明，共面圆轨道上轨道转移的最优解始终存在于遍历所有目标航天器扫过经度范围最小的序列中，且速度增量随着任务时间的上升而呈下降趋势。文献[14]给出了详细的证明过程，本文在此不再赘述。

2 基于聚类算法的任务分析

根据以上分析，轨道转移的成本估计是在假设从空间燃料站出发访问一个目标卫星，加注完毕即返回情况下的燃耗(速度增量)值。

如图3所示，方形代表燃料站，圆形代表目标航天器，箭头表明来回往返费用占绝大多数，这样的情况浪费了大量的时间与燃耗，而在现实中也几乎没有在轨加注任务会采用这种方式。因此这种加注成本预测方式与实际运营中的加注任务成本存在了较大的误差。目前“多对多”在轨加注任务的主要做法在服务航天器燃料充足的情况下，对一条路线上尽可能多的目标航天器进行一次性加注如图3(b)所示，这样使得轨道转移路线并不是辐射点式的路线，而是采用一种类似连续圈式的服务路线。

为了实现服务航天器能以连续圈式的服务路线往返于燃料站，本文在设计算法时运用聚类法对模型进行修正，首先对所有的目标航天器进行聚类分析，利用聚类法经若干次迭代后将各目标航天器划分为几类，每一类又由不同的空间燃料站供应燃料。由于每一空间燃料站负责的目标航天器不同，需要对每类中的目标航天器分别求解旅行商问题，得到经过该类中所有目标航天器的最短路径。其基本思想如下：

1)由假设的m个空间燃料站可知，目标航天器需要分成m类，利用k-Harmonic聚类法将所有目标卫星进行聚类分析，设得到的m类目标航天器集为S1(n1),S2(n2),…,Sm(nm)，各类中目标卫星的个数为nm。

2)在每个目标航天器集内部，求解一个旅行商问题，得到连接各样本点集内点的最短距离Bm，cij为第i个目标航天器到第j个空间燃料站的轨道转移燃料消耗。

3)cij代入m个无容量约束的选址模型子问题，解得每一类目标航天器服务顺序的最优解，然后将其相加即得原问题的解。

3 问题求解

3.1 适应度函数

本文算法优化目标是在满足时间约束下，总燃耗最小。总燃耗越小，适应度值越高，由以上分析可知可用速度增量代替燃耗质量，则令适应度值为

(7)

3.2 编码方式

算法中，采用混合编码的方式，将迭代算子分为两段处理，第一段描述目标航天器与空间燃料站的归属问题，则待优化的参数是m个空间燃料站的位置，使用二进制编码方式，由于聚类中心的数量为m，每条染色体分为m条代码段，对于m维的目标航天器样本向量，假定每个变量使用k位二进制编码，则染色体的总长度为m、n、k三者相乘的积；第二段描述服务航天器的最优路径问题，采用实数编码，长度为目标航天器的个数。选择算子采用随机遍历抽样；交叉算子采用单点交叉；变异算子采用随机产生两个变异位的方式。

3.3 基于模拟退火遗传算法的k-Harmonic聚类

算法求解过程如图4所示，首先设置初始退火温度等系数及随机产生初始的目标航天器分类，即初始种群，之后反复调用聚类算法的求解函数来计算适应度，依据适应度值选择较优的燃料站(聚类中心)与目标航天器分配关系，并由此生成新的种群，当满足停止条件时跳出，得到优化算法的结果。

4 仿真与结果分析

4.1 计算结果

在Matlab上对本文所构建的圆轨道航天器在轨加注任务调度的数学模型及模型求解算法进行数值仿真。由于GEO航天器轨道特性可以近似认为是圆轨道，目标航天器选择30个GEO航天器作为研究对象，轨道参数如表1所示。

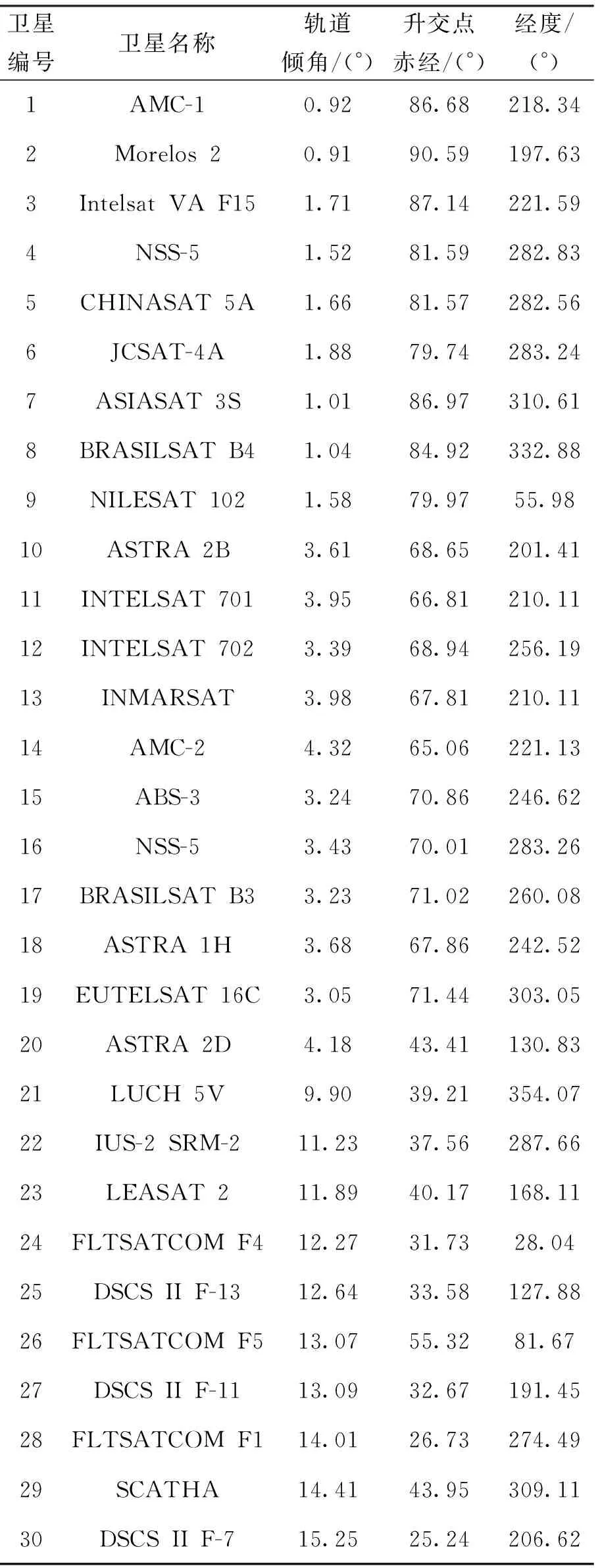
表1 GEO航天器的轨道根数

4.2 试验一

为了对照，将试验结果与单服务航天器的在轨加注策略进行比较，设服务航天器轨道半径为42 164 km，初始真近点角0°，初始轨道倾角0°干重3 000 kg，最大燃料携带量5 000 kg，初始时刻燃料携带量5 000 kg，推进系统比冲3 000 m/s，任务时间为3年。采用遗传算法进行求解，遗传算法相关参数，种群规模50，迭代代数200，交叉概率0.9，变异概率0.05，代沟0.9。运行程序后得到服务航天器对目标航天器加注的最优顺序为：

1→3→2→8→9→5→10→6→4→7→20→18→16→13→17→11→19→12→14→15→21→22→23→24→25→26→28→29→30→27，具体路径如图5所示，图6反映了服务航天器每次轨道机动的速度增量情况，横坐标与最优服务顺序对应。

服务航天器在整个加注过程中，轨道转移的总速度增量1.802 1 km/s，其中异面轨道转移总速度增量1.500 5 km/s；总燃耗3 666.11 kg，其中用于异面轨道转移的总燃耗为3 162.34 kg，占轨道转移总燃耗的86.38%。由于模型局限性，在不考虑在服务过程中燃料加注导致质量减轻的情况下，服务航天器最终仅有约1 333.89 kg燃料可用于加注服务，占航天器总质量的16.67%。

4.3 试验二

仍然取试验一中的30个GEO航天器作为目标航天器，3颗服务航天器从各个部署的空间燃料站出发，干重3 000 kg，最大燃料携带量5 000 kg，初始时刻燃料携带量5 000 kg。任务时间不变。

通过聚类算法获得空间燃料站的位置如图7、图8所示，表2给出了具体的位置参数。

优化计算的结果如下。

每颗服务卫星的最优服务顺序如下：

-1→8→1→2→7→3→6→5→9→4→-1

-2→11→13→14→20→19→17→15→12→16→10→18→-2

-3→25→24→27→28→30→29→26→21→22→23→-3。

其中-1，-2，-3分别代表算法中负责对该目标航天器群供给燃料的空间燃料站编号。每颗服务航天器加注过程中服务顺序和每次轨道转移的速度增量如图9所示，表3给出了燃料消耗情况。

服务航天器在整个加注过程中，轨道转移的总速度增量：1.403 2 km/s，其中异面轨道转移总速度增量：1.285 1 km/s，总燃耗3 152.91 kg，其中用于异面轨道转移的总燃耗为2 895.24 kg，占轨道转移总燃耗的91.83%。服务航天器最终有约11 847.09 kg燃料可用于加注服务，占所有服务航天器总质量的78.98%。

空间燃料站编号hx/(km2·s-1)hy/(km2·s-1)经度/(°)13245.80-509.64286.0927701.38-3288.94215.09316140.32-23460.53180.36

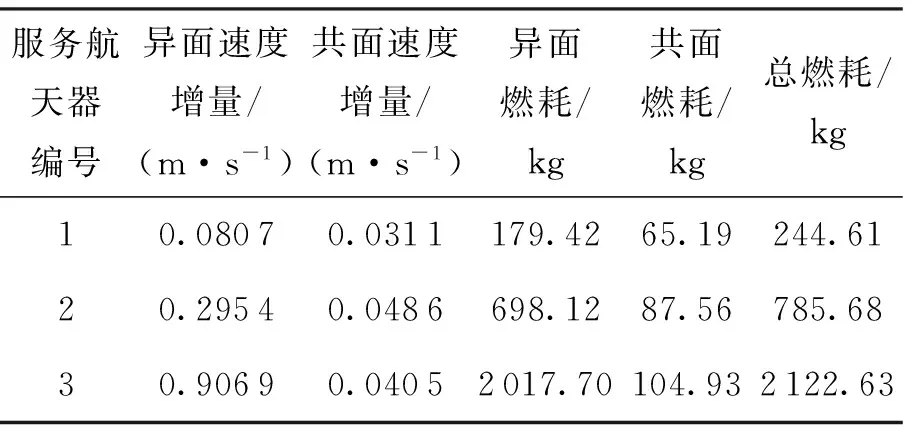
表3 各服务航天器速度增量与燃料消耗

4.4 结果分析

如图10所示，各代总燃耗平均值总体上处于逐渐减少的趋势，各代所有解中的最优解随着迭代次数的增加，呈单调递减性质，且逐渐收敛，说明本文针对圆轨道航天器在轨加注任务空间燃料站部署的优化算法可行。

由试验一和二的结果对比可知，当需要补加燃料的目标航天器较多时，采用单服务航天器进行燃料加注的效率极低，在任务时间相同、服务航天器规格相同的情况下，若空间中已经部署有可为服务航天器补充燃料的空间燃料站时，由于服务范围被控制在轨道根数相近的目标航天器群内，服务航天器可以节约由于较大倾角异面变轨带来的燃料损失，提高燃料的利用率。由于服务航天器的目标范围小且固定，任务的容错性和灵活性也较高。由于有空间燃料站的支持，服务航天器也可以摆脱自身燃料上限的束缚，减少自身质量也可以达到减少轨道转移燃耗的目的，促进轨道转移飞行器向着小而快速的方向发展。

5 结束语

本文分析了基于空间燃料站的在轨加注任务模式，介绍了在轨燃料加注任务中各类航天器的轨道部署，服务航天器进行在轨燃料加注服务时的任务流程；梳理了圆轨道航天器在轨燃料加注数学模型的变量和约束条件，将各变量符号化，结合约束条件和优化目标，将地面运输系统的概念引入航天器在轨加注任务的数学模型，提出了多空间燃料站、多服务航天器、多目标航天器的空间服务模式，并运用多学科的理论、方法和成果，为该类问题的研究提供了新的思路。并在Matlab上对本文构建的数学模型和模型求解方案进行了数值仿真试验，对得到的仿真结果进行了分析，验证了方案的可行性。

面对未来越来越频繁的太空任务，航天器在轨加注成为在轨服务技术的重要一环。在本文的研究基础上，可以进一步地将地面运输系统理论及调度算法与在轨服务体系相结合，考虑更多的约束条件，使得这项技术向着自主化与智能化的方向发展。

References)

[1] NAKASUKA S，TANABE T，SUMINO N. Fuel station-based transportation network as a future space infrastructure[J]. The Journal of Space Technology and Science，1992，8(2): 2_22-2_37.

[2] NAKASUKA S. Effects of space fuel station on the transportation system capability and cost-Two case studies[J]. Transactions of the Japan Society for Aeronautical & Space Sciences，1992，34(106):226-239.

[3] 蒙波，叶立军，韩潮. 卫星星座组网过程的策略规划[J]. 宇航学报，2009，30(1):150-154.MENG B，YE L J，HAN C. Programming of satellite constellation establishment strategy[J]. Journal of Astronautics，2009，30(1):150-154(in Chinese).

[4] 蒙波，徐盛，黄剑斌，等. 对GEO卫星在轨加注的服务航天器组网方案优化[J]. 中国空间科学技术，2016，36(6):14-21.

MENG B，XU S，HUANG J B，et al.Scheduling of satellite constellation for on-orbit refueling in GEO[J]. Chinese Space Science and Technology，2016，36(6):14-21(in Chinese).

[5] 欧阳琦，赵勇，陈小前. 共面圆轨道航天器在轨服务任务规划[J]. 中国空间科学技术，2010，30(1):34-40.

OUYANG Q，ZHAO Y，CHEN X Q. Programming of on-orbit service mission for multiple object spacecraft in coplanar circular orbits[J]. Chinese Space Science and Technology，2010，30(1):34-40(in Chinese).

[6] TSIOTRAS P，NAILLY A. Comparison between peer-to-peer and single spacecraft refueling strategies for spacecraft in circular orbits[C]. Infotech at Aerospace Conference，Arlington，Virginia，26-29 September，2005:26-29.

[7] SHEN H，TSIOTRAS P. Peer-to-peer refueling for circular satellite constellations[J]. Journal of Guidance，Control，and Dynamics，2005，28(6):1220-1230.

[8] DUTTA A，TSIOTRAS P. Asynchronous optimal mixed P2P satellite refueling strategies[J]. The Journal of the Astronautical Sciences，2006，54(3-4):543-565.

[9] DUTTA A，TSIOTRAS P. A greedy random adaptive search procedure for optimal scheduling of p2p satellite refueling[C]∥AAS/AIAA Space Flight Mechanics Meeting，Sedona，Arizona，January 28-February 1，2007: 07-150.

[10] 冯全胜，徐波. 基于伴飞模式的补给星轨道设计与优化[J]. 宇航学报，2011，32(1): 39-45.

FENG Q S，XU B. Orbit design and optimization of supplying satellite based on formation flight mode[J].Journal of Astronautics，2011，32(1): 39-45(in Chinese).

[11] 肖东东，徐波，高有涛，等. 基于伴飞模式的异面星座补给轨道优化[J]. 中国科学: 物理学，力学，天文学，2013，42(12): 1327-1337.

XIAO D D，XU B，GAO Y T，et al. Orbit optimization of supplying satellite of non-coplanar constellation based on formation flight mode[J]. Scientia Sinica Physica，Mechanica & Astronomica，2013，42(12): 1327-1337(in Chinese).

[12] 唐国金，罗亚中，张进. 空间交会对接任务规划[M]. 北京：科学出版社，2008.TANG G J，LUO Y Z，ZHANG J. Mission planning for rendezvous and docking[M]. Beijing Science Press，2008(in Chinese).

[13] 欧阳琦，姚雯，陈小前. 地球同步轨道卫星群在轨加注任务规划[J]. 宇航学报，2010，31(12):2629-2634.

OU Y Q，YAO W，CHEN X Q. Mission Programming of On-Orbit Refueling for Geosynchronous Satellites[J]. Journal of Astronautics，2010，31(12):2629-2634(in Chinese).

[14] SHEN H，TSIOTRAS P. Optimal scheduling for servicing multiple satellites in a circular constellation[C].AIAA/AAS Astrodynamics Specialist Conference， Monterey, California，5-8 August，2002: 5-8.

(编辑：车晓玲)

Mission scheduling for multiple spacecraft refueling based on space fuel station in circular orbits

ZHU Xiaoyu1，QIAO Bing1，*，ZHANG Qingzhan2，JIN Yongqiang2，Tan Yinglong1

1.CollegeofAstronautics，NanjingUniversityofAeronauticsandAstronautics，Nanjing210016，China2.InstituteofAerospaceSystemEngineeringShanghai，Shanghai201109，China

As the development of space technology，the demand for space transportation system becomes larger and more various，on-orbit refueling has been a new and independent developing direction in order to reduce the launch costs，mitigate space debris and improve the payload of launch vehicle. The development of methodologies was focused to generate optimal trajectories and schedules for refueling constellations of refueling spacecraft. An on-orbit reusable refueling policy and its mission scheduling for multiple spacecraft in circular through a space fuel station were presented. In order to establish the scheduling model for the on-orbit refueling of multiple circular spacecraft orbit through a space fuel station，the relationship between the velocity change and orbital elements for transferring of service spacecraft was firstly obtained based on the analysis of the problem of two impulses orbital maneuver. A multi-objective optimization model for mission scheduling of on-orbit refueling for multiple spacecraft in circular orbits was developed to optimize both the sequence and time distribution of the refueling mission，and a specifical design algorithm was employed to search the solutions to the multi-objective optimization problem. To verify the effectiveness of the proposed scheduling algorithm，a computer simulation that aims at scheduling a mission of on-orbit refueling for 30 spacecraft in circular orbits was conducted.

circular spacecraft；on-orbit refueling；mission scheduling；multi-objective programming；cluster analysis；space fuel station

10.16708/j.cnki.1000-758X.2017.0067

2016-11-26；

2016-12-30；录用日期：2017-01-24；网络出版时间：2017-05-31 10:39:33

http:∥kns.cnki.net/kcms/detail/11.1859.V.20170531.1039.006.html

上海航天创新基金(2015019)；南京航空航天大学校开放基金(KFJJ20151506)

朱啸宇(1992-)，男，硕士研究生，963374058@qq.com,研究方向为航天器在轨服务

*通讯作者：乔兵(1967-)，男，博士，副教授，bqiao@nuaa.edu.cn，研究方向为智能机器人学、空间机器人、航天器自主在轨服务技术和模块化航天器设计

朱啸宇，乔兵，张庆展，等. 圆轨道航天器在轨加注任务空间燃料站部署问题[J].中国空间科学技术，2017，37(3)：35-43.ZHUXY，QIAOB，ZHANGQZ，etal.Missionschedulingformultiplespacecraftrefuelingbasedonspacefuelstationincircularorbits[J].ChineseSpaceScienceandTechnology，2017，37(3)：35-43(inChinese).

V412.4+1

A

http:∥zgkj.cast.cn