三维CSG-BRep拓扑模型的研究
2017-07-01朱春晓倪春迪
朱春晓,黄 明,倪春迪
(1.黑龙江工程学院 测绘工程学院,黑龙江 哈尔滨 150050;2.北京建筑大学,北京 100044)
三维CSG-BRep拓扑模型的研究
朱春晓1,黄 明2,倪春迪1
(1.黑龙江工程学院 测绘工程学院,黑龙江 哈尔滨 150050;2.北京建筑大学,北京 100044)
针对目前通过离散点云来构建的三角网模型具有数据量大,难以拆分,没有拓扑关系等缺点,提出一种特殊的CSG-BRep模型数据结构,该数据结构可以全面细致地记录模型内部的拓扑关系。利用激光雷达点云作为模型的数据来源,结合文中提出的数据结构,构建三维精细CSG-BRep拓扑模型。该模型与普通三角网模型相比,各个构件可以拆分,所占用内存较少,并具备更完善的拓扑关系。
拓扑关系;激光雷达点云;CSG-BRep模型;数据结构
三维空间拓扑关系的研究对GIS数据建模、空间查询、空间分析过程都具有举足轻重的意义。目前,很多学者对三维模型拓扑关系的表达和构建进行了研究,如李霖,赵志刚,郭仁忠等提出体对象之间三维拓扑的构建[1];邵振峰,李德仁,程启敏提出通过体和影像来实现三维拓扑重建[2];吴长彬,闾国年分析了现阶段空间拓扑关系的若干问题[3];Patrick Erik Bradley, Norbert Paul提出了一种G映射方法来表达空间的拓扑结构[4];Simon Daum提出一种基于边界表示BRep的方法来分析建筑信息模型BIM的拓扑信息[5];Zhuojun Bao, Hans Grabowski提出一种将BRep转化为精确二叉树的方法来处理空间信息[6]等等。
但是,目前对三维空间拓扑的研究还处于初期阶段,虽然专家学者提出了各自的拓扑模型,但是还没有好的方法来实现拓扑结构的访问[7]。对三维模型内部拓扑结构的研究更是寥寥无几。上述文献中存在的问题主要有以下五点:①都是假设模型已经存在,再去探究拓扑关系。②都是只提出各自的拓扑模型,并无探究如何访问拓扑。③对相邻空间体拓扑重建虽有较好的方法,但是在处理相交空间体的拓扑关系重建困难。④多数拓扑模型存在数据冗余,拓扑与几何信息融合不全面的现象。本文针对这些问题,按照面向对象的思想,设计了一套系统的拓扑元素表达,提出一种CSG-BREP拓扑模型来描述模型内部的拓扑关系。
1 基于CSG-BRep建立拓扑模型
1.1 CSG-BRep模型拓扑元素
模型是由基本要素构成的,这些基本要素被抽象为点、边、面、环、壳、体和复杂体以及复合体,呈现出由简单到复杂的递进关系,如表1所示。

表1 拓扑各要素及其意义
1.2 拓扑模型结构
模型之中包含有复杂的拓扑连接关系[8-11]。利用构造实体几何的方法(CSG)可以方便地处理不同模型之间的拓扑构建,但是,单一的CSG表示方法局限到最小单元仅仅为体模型,并不能体现模型内部拓扑关系。本文提出CSG与BRep结合的方式来建立拓扑模型。实体的边界是由面的并集来表示,而每个面由它所在的曲面的定义加上其边界来表示,面的边界是边的并集,边又由点来表示,如图1所示。
拓扑中,顶点可以组成边,边可以组成环,环又可以构成面,面在进一步组成壳或者体。由较低层级的拓扑对象逐级构建成较高层级的拓扑对象,中间不可跨级组建。不可通过拓扑对象边直接构建面或者壳对象(顶点构环,面构体除外)。同时,由不同的体(solid)可以组建成复杂体(compsolid),而由上述的所有拓扑对象可以统一组成复合体(compound)。
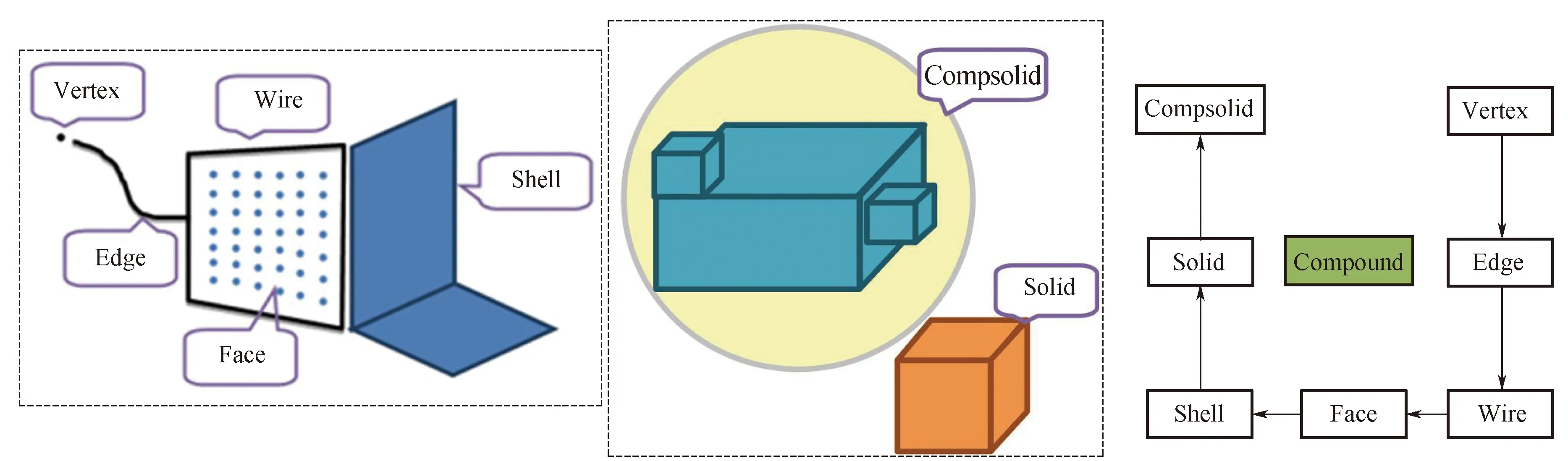
图1 基于CSG-BREP的拓扑模型结构
上级的拓扑元素包含对该元素下级拓扑元素的引用。所有的引用都是从复杂的拓扑元素到简单的拓扑元素。同时,简单的拓扑元素可以被不同的复杂的拓扑元素共享。以一个复杂体为例,按照本文提出的拓扑模型来描述复杂模型内部的拓扑关系,如图2所示。
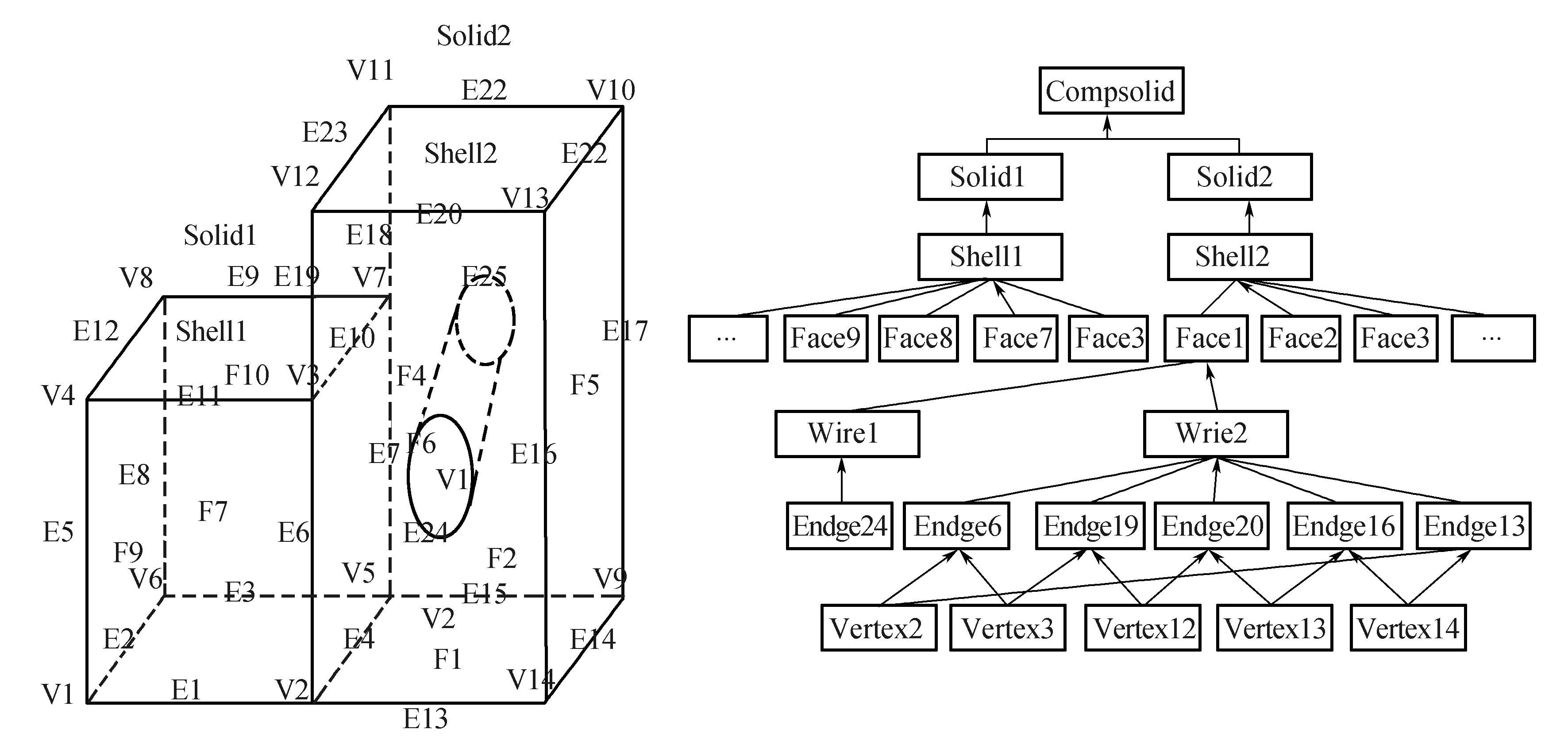
图2 拓扑模型描述复杂体实例
在拓扑模型中,只有3种拓扑对象与几何对象直接相关联:顶点(vertex)、边(edge)、面(face),分别为Geo_Vertex、Geo_Edge、Geo_Face。另外,顶点、边、面分别被分配一个容差(Tolerance)值,用于判定在误差范围内顶点、边和面是否生成。顶点容差T的几何意义为以顶点为圆心半径为T的球。这个球必须包含所有与这个顶点相连边的曲线端点。边的容差是其三维曲线和其他任何表示方式之间的最大偏差。其几何意义就是以容差为半径沿边的一个包含边的三维曲线及其他任何形式表示的管子。面的容差的几何意义是包围面的一个具有厚度的板。通常情况下,必须满足以下条件:当边位于面上,顶点位于边上时,面的容差≤边的容差≤顶点的容差。通过几何点线面基本对象可以进一步关联到更复杂的几何对象,那么,拓扑信息和几何信息就完全直接或间接地关联起来。与拓扑对象元素相关联的几何元素以及容差值的关系如图3所示。
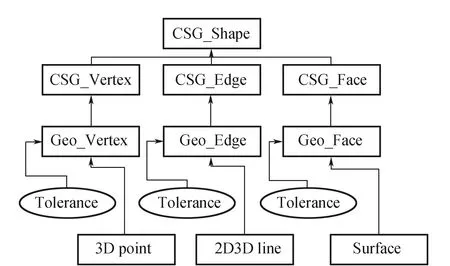
图3 拓扑对象元素的几何信息
拓扑元素中,每一个元素都属于实体(模型本身)的对象。其位于中间层级的拓扑对象同时具有与其相联接的父级和子级拓扑对象。因此,拓扑关系的访问也分为两种:一种是访问拓扑对象本身与其父级拓扑对象的连接关系,另一种是访问拓扑对象本身与其子级拓扑对象的连接关系。本文实现这两种拓扑关系的访问。其中任意拓扑对象中包含3个变量,拓扑位置CSGLocation,拓扑朝向CSGOrientation和子集实体CSG_Subshape。如图4所示,子集实体中记录和shape相连接的子集拓扑对象,位置记录拓扑对象相对于世界坐标系的旋转矩阵,朝向记录拓扑对象之间的方位。
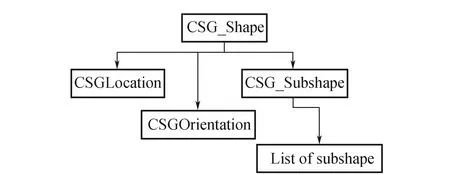
图4 shape成员变量组成关系
1.3 拓扑位置及方向
为了跟踪拓扑元素的位置,每个形状都定义一个局部坐标系CSGLocation,如图4所示。局部坐标系可以通过如下两种方式来表示:①右手法则表示的3个互相垂直的向量;②相对于世界坐标系的变换。位置变量表示了初等矩阵经过一系列变换后得到的坐标系,用于保存累积变换后的结果,这能避免矩阵变换的重新计算。
拓扑方向对于记录拓扑元素的方位具有极其重要的作用,并且拓扑方向和边界具有紧密的联系。本文采用参数方程来设计空间曲线、曲面,需要用到拓扑方向的shape有3种:通过顶点约束的曲线,通过边约束的曲面和通过面约束的空间。不管是哪一种shape(该shape本身作为维数更高的空间几何区域的边界),都定义两个局部段,其中一个被指定为默认段。对于一条通过顶点约束的曲线,首先曲线的参数表示必须给出曲线的一个方向(自然方向),如设a≤u≤b,曲线C(u)方向为从C(a)到C(b),而该曲线的默认段就是沿着曲线方向的一些列比顶点参数大的点的集合。对于一个通过边约束的曲面,该曲面的默认段位于边前进方向的左侧。边的前进方向是指边的自然方向,即逆时针方向。对于一个通过面约束的空间,该空间的默认段位于曲面法向相反的一侧。
1.4 拓扑遍历
根据以上CSG-BREP拓扑模型的定义,拓扑访问包括shape的子集拓扑结构及shape的父集拓扑结构的遍历。
子集遍历,因为任意一个拓扑对象shape中直接包含了变量CSG_Subshape,而CSG_Subshape中包含了一个shape的列表,该列表中存放的是拓扑对象子集的集合,所以,直接从该集合中遍历所需要查找的拓扑类型即可。另外,如果一个拓扑元素被多次引用的话,那么可能会遍历该元素多次。
父集遍历,CSG-BRep模型的拓扑数据结构中,都是从上向下(从CSG_Shell或CSG_Solid到CSG_Vertex)的引用,不能像访问子集拓扑结构那样直接从子集元素来访问该子集的父级元素。需根据边,遍历顶点并对顶点编码,建立顶点与边的映射,最后从顶点-边的映射中提取父集。
2 实验及结果
本文利用VS2010作为开发环境,利用C++语言进行编程,本实验的数据源为利用三位激光扫描仪获取的点云数据,通过对点云数据拟合出基本体素长方体、圆柱体等,构建出具有拓扑关系的故宫太和门大木结构CSG-BRep模型,如图5所示。为了做比较,同时用第三方软件Geomagic Studio12生成大木结构的三角网模型,如图6所示。

图5 CSG-BRep大木结构模型

图6 普通三角网大木结构模型
通过拓扑访问,查询分析该CSG-BRep大木结构模型,可以获得该模型共包含81个圆柱体,148个长方体,模型可拆分,具有详细的拓扑关系,占用内存的大小为336 KB。而根据离散点直接生成的普通三角网大木结构模型,共包含3 991个点,7 475个三角面片,模型不可拆分,只包含三角形3个顶点的连接关系,无完整的拓扑关系。占用内存的大小为1 986 KB。
通过对比可知,本文提出的三维精细CSG-BRep模型,不仅有效地减少了数据量,而且模型可拆分,各部分构件清晰明了,并且具备可查询分析的拓扑关系。
3 结 论
本文设计了基于CSG-BREP的拓扑数据模型,该数据模型中包含了拓扑元素的组成关系,拓扑元素与几何元素的结合,并按照面向对象的思想,实现了三维模型生成,取得了较好的效果。基于CSG-BREP的拓扑数据模型,模型元素之间的连接关系清楚,有利于三维空间拓扑关系的查询分析。该方法解决了目前大部分模型如三角网模型没有详细拓扑关系,以及仅具有拓扑模型但不能自由访问拓扑结构的问题。
[1] 李霖,赵志刚,郭仁忠,等. 空间体对象间三维拓扑构建研究[J].武汉大学学报(信息科学版),2012,37(6):719-723.
[2] 邵振峰,李德仁,程起敏. 基于航空立体影像对的复杂房屋三维拓扑重建[J]. 武汉大学学报(信息科学版),2004,29(11):999-1003.
[3] 吴长彬,闾国年.空间拓扑关系若干问题研究现状的评析[J].地球信息科学学报,2010,12(4):524-531.
[4] BRADLEY P E, PAUL N. Comparing G-maps with other topological data structures[J]. Springer Journal of GeoInformatica,2014(3).
[5] DAUM S, BORRMANN A. Processing of Topological BIM Queries using Boundary Representation Based Methods[J]. Elsevier Journal of Advanced Engineering Informatics, 2014.
[6] BAO Zhuojun, GRABOWSKI H. Converting boundary representations to exact bintrees[J]. Elsevier Journal of Computers in Industry, 1998,37(1).
[7] LIU K,SHI W Z. Extended Model of Topological Relations between Spatial Objects in Geographic Information Systems[J]. International Journal of Applied Earth Observation and Geoinformation, 2007, 9: 264-275.
[8] NONAKA Hideki, OHSAWA Yutaka. A Method of Caching Topology on Implicit Topology Model[J]. J-STAGE Journals of Theory and Applications of GIS, 2003,11(1).
[9] NIAN Rui, HE Bo, LENDASSE A. 3D object recognition based on a geometrical topology model and extreme learning machine[J]. Springer Journal of Neural Computing and Applications, 2013,22(3).
[10] 贺彪,李霖,郭仁忠,等. 顾及外拓扑的异构建筑三维拓扑重建[J]. 武汉大学学报(信息科学版),2011,36(5):579-583.
[11] 张海荣,余劲松弟,刘云生,等. 基于空间推理的巷道三维拓扑建立[J]. 地理与地理信息科学,2009,25(4):53-55.
[责任编辑:刘文霞]
Research on the topological model of three-dimensional CSG-BRep
ZHU Chunxiao1,HUANG Ming2,NI Chundi1
(1.College of Surveying and Mapping Engineering,Heilongjiang Institute of Technology,Harbin 150050,China;2.Beijing University of Civil Engineering and Architbcture,Beijing 100044,China )
Currently ordinary triangular mesh model based on discrete point cloud has a large amount of data. This model is not only difficult to split, but also lacks of topological relations. To solve these problems, this paper presents a CSG-BRep topological model . It can record topological relationship of 3D model in great detail. Finally, LIDAR point cloud is used as a data source to construct 3D CSG-BRep topological model. Compared with the ordinary triangular mesh model, the model components can be split, which can effectively reduce the amount of data. In addition, the CSG-BRep model has the detailed topological relations.
topological relation;LIDAR;CSG-Brep model;data structure
2017-01-09
黑龙江省教育厅科学技术研究资助项目(12531566)
朱春晓(1965-),女,高级工程师.
著录:朱春晓,黄明,倪春迪.三维CSG-BRep拓扑模型的研究[J].测绘工程,2017,26(8):20-23.
10.19349/j.cnki.issn1006-7949.2017.08.005
P208
A
1006-7949(2017)08-0020-04
