基于PSO的PID参数优化及其工程实现

要亚斌，王利杰，王佳荣

(1.河北省电力勘测设计研究院，石家庄 050031；2.国网河北省电力公司电力科学研究院，石家庄 050021；3.青岛鸿瑞电力工程咨询有限公司，山东 青岛 266100)



基于PSO的PID参数优化及其工程实现

要亚斌1，王利杰2，王佳荣3

(1.河北省电力勘测设计研究院，石家庄 050031；2.国网河北省电力公司电力科学研究院，石家庄 050021；3.青岛鸿瑞电力工程咨询有限公司，山东 青岛 266100)

介绍运用粒子群优化算法(PSO)对单回路和双回路系统PID控制器参数的优化，并进行数字仿真，得出控制品质参数。分析在被控对象的表达形式为n阶惯性环节加纯迟延和一阶惯性环节串联2种不同情况下，采用粒子群优化算法寻优的方法，说明根据给定被控对象参数计算出PID参数以及相应的仿真曲线和控制品质数据的工程实现过程。

PID控制器；参数优化；参数整定；粒子群优化算法

1 概述

PID控制器是工程实际中应用最为广泛的控制器[1]，其结构简单、容易实现、并且具有较强的鲁棒性，成为工业控制的主要技术之一。自PID控制器提出以来，人们便致力于PID整定方法的研究，涌现出了各种各样的方法。随着计算机技术的发展，一些新的智能算法得到了迅速发展和广泛应用[2-4]，并在理论和应用方面都有重要的意义。在这些算法中，粒子群优化算法(PSO)是近年来发展起来的一种较为实用的进化算法[5-7]，它基于群体智能理论，通过群体中粒子间的合作与竞争产生的群体智能指导优化搜索，具有很强的搜索能力。PSO作为一种强大的优化工具已被广泛应用于优化问题的求解[3]。以下利用PSO算法，实现了单回路和双回路系统的PID控制器优化。在此基础上，开发出了一套PID控制器优化程序，为PID控制系统的参数整定提供了一个简单、方便的平台。

2 PSO对PID参数优化的方法

PSO 算法属于进化算法的一种，和遗传算法相似，它也是从随机解出发，通过迭代寻找最优解，通过适应度来评价解的品质，但它比遗传算法规则更为简单，没有遗传算法的“交叉”和“变异”操作，它通过追随当前搜索到的最优值来寻找全局最优。

在PSO算法中, 每个粒子代表解空间的一个候选解,粒子在搜索空间以一定的速度飞行,飞行速度根据飞行经验进行动态调整。该算法基于群智能的并行全局搜索策略,采用速度位搜索模型实现对整个空间的寻优操作。PSO算法是模仿生物社会性行为而得出的一种全局优化算法,是一种高效、简单的并行搜索算法,其优点在于概念简单、实现容易、鲁棒性好,并且能以较大概率收敛到全局最优,而且它对所优化目标的先验知识要求甚少,一般只需知道其数值关系即可。但是该算法的惯性权重对算法性能具有很大的影响,另外,在初始群体的生成上,它是根据经验估计出PID 3个参数的取值范围,并在此范围内采用随机生成的方式,对其可行解空间进行搜索的,因此需要合理估计PID 3个参数的取值范围。

假设在一个D维的目标搜索空间中有m个粒子组成一个群体，其中第i个粒子的位置表示为向量xi=(xi1,xi2,…xiD)，(i=1,2,…，m),其速度也是一个D维的向量vi=(vi1,vi2,…viD)。第i个粒子群搜索到的最优位置为Pg=(pg1,pg2,…,pgD)粒子群公式如下：

vid(t+1)=vid+c1r1(pid-xid(t))+c2r2(pgd-xid(t))

(1)

xid(t+1)=xid(t)+vid(t+1)

(2)

式中：i=1,2,…m，d=1,2,…,D；加速常数c1和c2为非负常数；r1和r2服从[0,1]上的均匀分布随机数；vid(t)是第i个粒子当前位置；Pid是第i个粒子的当前速度；vid∈[-Vmax,Vmax],Vmax为最大限制速度，是非负数，当vid>Vmax时，取vid=Vmax，当vid<-Vmax时，取vid<-Vmax。

鉴于蚁群算法具有分布式并行搜索能力，且易于与其它算法结合，是一种全局优化的算法。因此，可以利用蚁群算法的全局优化能力优化PID参数,得到PID参数的初始值,然后根据系统当前的误差和误差变化率,用模糊推理方法在线优化调整PID参数的权值来动态地调整参数。基于粒子群的PID参数优化的基本思想：将PID 3个参数组合在一起设为粒子群的粒子，在搜索空间中每一个粒子以一定的速度飞行，飞行过程中每个微粒飞行速度将依据微粒的飞行经验和群体的飞行经验进行动态调整，以一定的速度向目标逼近,最后找到最优目标,即PID控制器的最优参数。

3 工程实现

3.1 单回路热工系统PID整定及其工程实现 单回路控制系统是最简单、最基本、也是使用最广泛的一种形式，单回路系统框图见图1。对于控制系统来说，在设定值发生变化或系统受到扰动作用后，系统将从原来的稳态经历一个过程进入另一个新的稳态。一个自动控制系统的好坏在稳态下是难以判别，只有在过渡过程中才充分反映出来。一个良好的控制系统，在经历扰动后，一般应平稳、迅速和准确地趋近或恢复到设定值。这就需要对调节器的控制参数进行准确的设定才能达到理想的效果，而PID 调节器在出厂时一般都不会提供现成的PID 参数，它们只能由技术人员在生产过程中根据实际情况自己摸索出来。

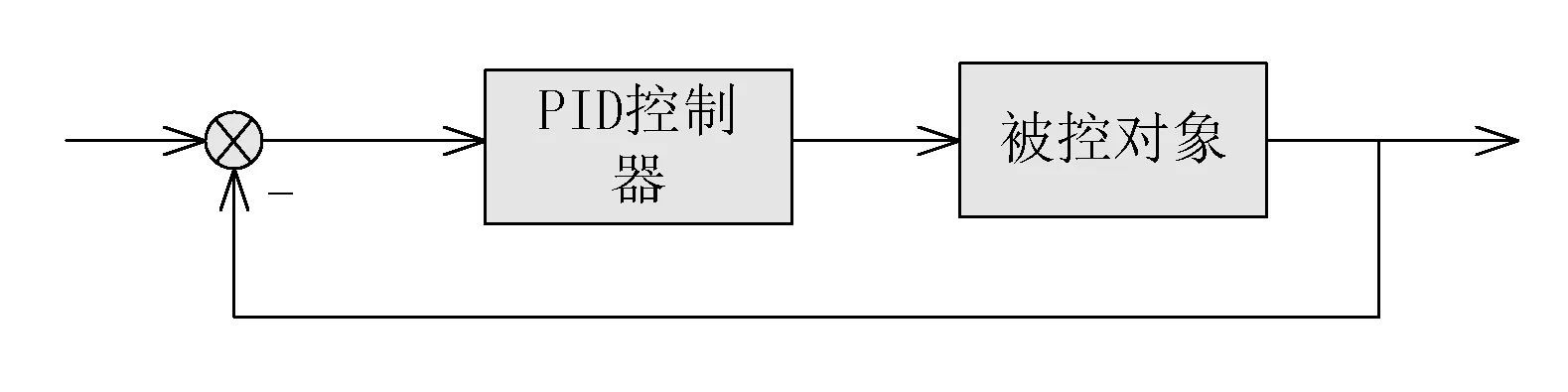
图1 单回路系统框图

文章所提供的方法就是用最优算法，可以通过被控对象的参数计算出一种理论上的PID调节参数，并将计算出的PID参数带入控制系统进行仿真，得到这组PID参数的调节效果。使得系统在调试时，可以方便顺利的找到最优的参数值。

3.1.1 n阶惯性环节加纯迟延

在单回路控制系统中，当被控对象为n阶惯性环节加纯迟延，即被控对象的传递函数表达形式为：

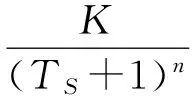
(3)

通过给定的K、T、n及τ的值，运用粒子群优化算法，反算出PID控制器的优化参数：Tp、KI、Kd以及阶跃响应曲线的超调量、调节时间和衰减率。

在热工控制系统中被控对象为n阶惯性环节加纯迟延的时候，传递函数为式(3)时，这只是自平衡过程的传递函数。非自平衡对象应加一个积分环节。

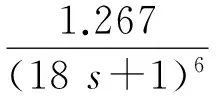
表1 有自平衡并带有纯迟延系统优化计算结果

KpKiKd超调量/%调节时间/s衰减率/%0.495270.0067608.83452.6490.18

当被控对象传递函数为：

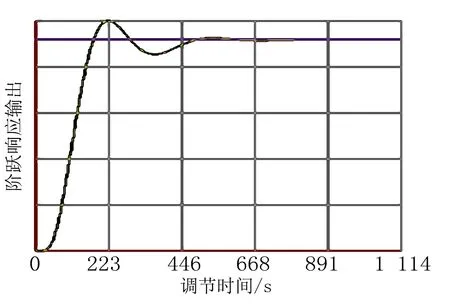
图2 有自平衡并带有纯迟延系统优化后的单位阶跃响应曲线

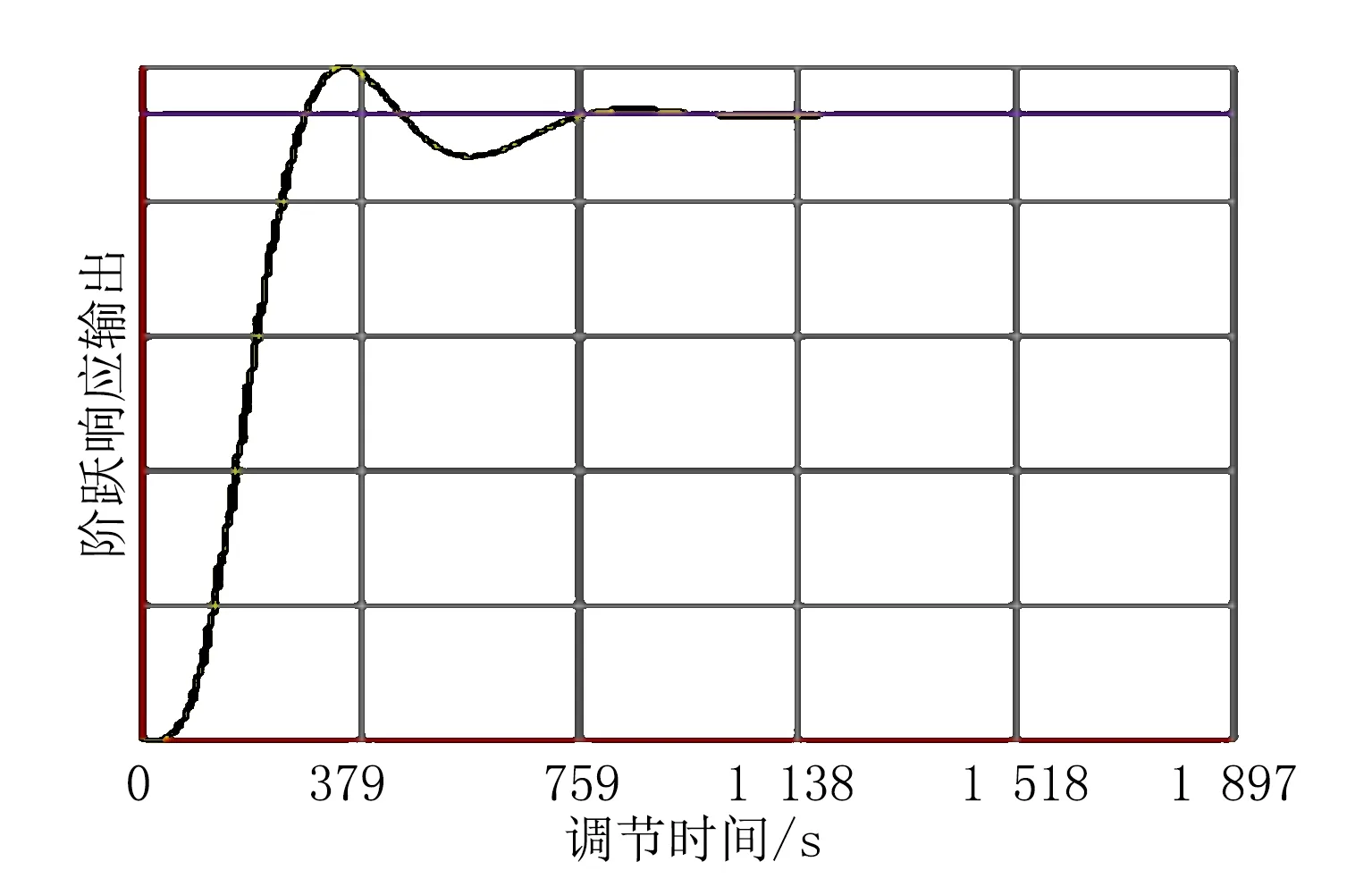
图3 有自平衡优化后的单位阶跃响应曲线

表2 有自平衡系统优化计算结果

KpKiKd超调量/%调节时间/s衰减率/%0.521680.0044407.34717.0790.92

3.1.2 一阶惯性环节串联

如果被控对象的传递函数形式不是n阶惯性环节加纯迟延的形式，而是由一阶惯性环节串联形式，对程序中做了相应的功能，可以计算这种形式。

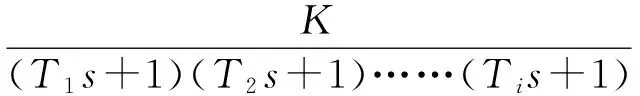
(4)

例如被控对象传递函数如为以下表示时

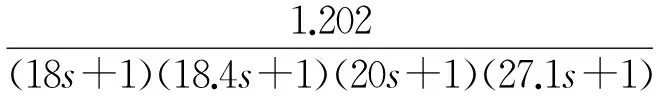
(5)

输出的结果见图4和表3。

图4 一阶惯性环节串联系统PID优化后的单位阶跃响应曲线

表3 一阶惯性环节串联系统优化计算结果

KpKiKd超调量/%调节时间/s衰减率/%0.591740.0107204.38320.6497.48

当被控对象传递函数表达式为：

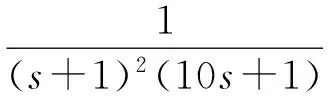
图5 3个环节串联系统PID优化后的单位阶跃响应曲线

表4 3个环节串联系统优化计算结果

KpKiKd超调量/%调节时间/s衰减率/%10.1176714.4327.698.86

从图2-5及表1-4可以看出，通过PSO优化方法，可以获取单回路系统的PID优化参数，并且取得了较好的优化效果。证明了软件可以有效解决单回路系统的PID控制器优化问题。

3.2 双回路(串级)热工控制系统PID整定及其工程实现

串级系统是由2只调节器串联起来工作，其中一个调节器的输出作为另一个调节器的给定值的系统。前一个调节器称为主调节器，它所检测和控制的变量称主变量(主被控参数)，即工艺控制指标；后一个调节器称为副调节器，它所检测和控制的变量称副变量(副被控参数)，是为了稳定主变量而引入的辅助变量。

整个系统包括2个控制回路，主回路和副回路。副回路由副变量检测变送、副调节器、调节阀和副过程构成；主回路由主变量检测变送、主调节器、副调节器、调节阀、副过程和主过程构成。当扰动发生时，破坏了稳定状态，调节器进行工作，见图6。根据扰动施加点的位置不同，分3种情况进行分析：扰动作用于副回路；扰动作用于主过程；扰动同时作用于副回路和主过程。

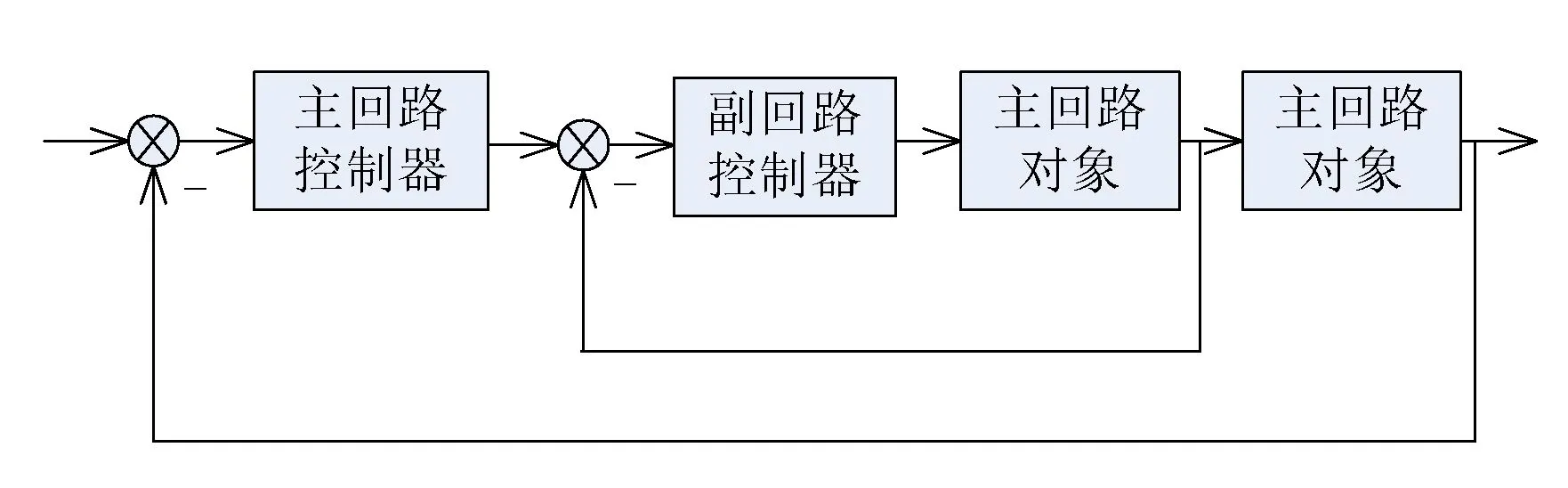
图6 双回路系统示意

3.2.1 n阶惯性环节加纯迟延

当串级系统内外回路的被控对象也就是主副被控对象的传递函数表达式都为n阶惯性环节加纯迟延的时候。

测试的被控对象1为：

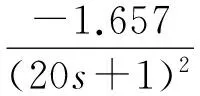
(6)

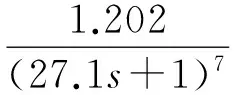
(7)

程序输出结果见图7和表5。

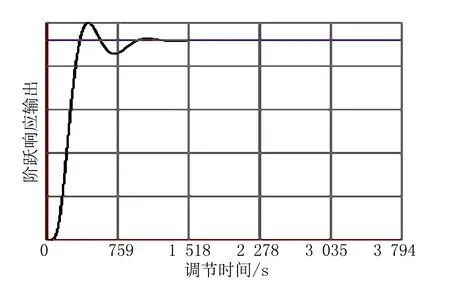
图7 双回路系统PID优化后的单位阶跃响应曲线

表5 双回路系统优化计算结果

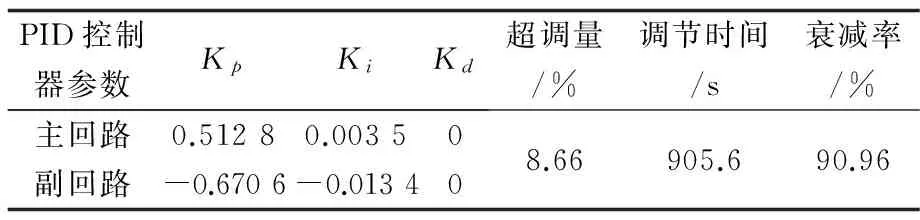
PID控制器参数KpKiKd超调量/%调节时间/s衰减率/%主回路0.51280.00350副回路-0.6706-0.013408.66905.690.96

测试的被控对象2为：

(8)

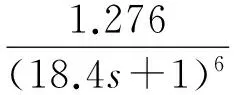
(9)

程序输出结果见图8和表6。

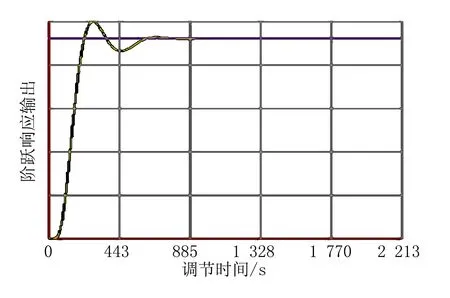
图8 具有负调特性双回路系统PID优化后的单位阶跃响应曲线

表6 具有负调特性双回路系统优化计算结果

PID控制器参数KpKiKd超调量/%调节时间/s衰减率/%主回路0.55220.00530.1534副回路-1.3633-0.027808.15567.3693.61

3.2.2 一阶惯性环节串联

当被控对象的传递函数不是n阶惯性环节纯迟延表达形式的时候，可以转换成一阶惯性环节串联的形式，这里还用在单回路中用到的传递函数。

副回路传递函数为：

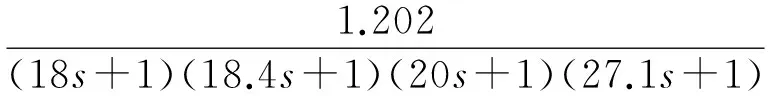
(10)

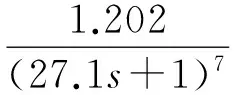
(11)

程序结果见图9和表7。

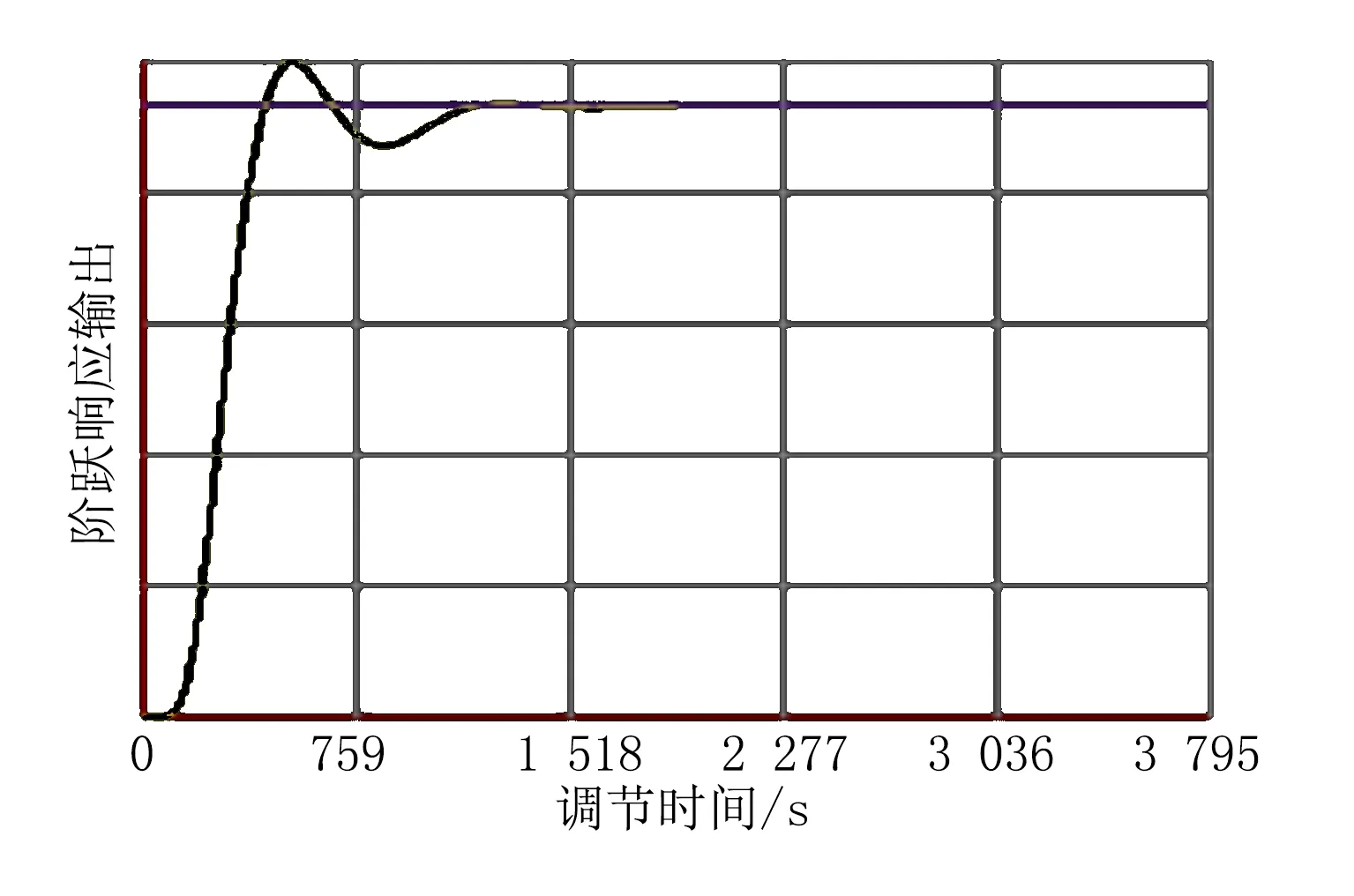
图9 混合形式传递函数双回路系统PID优化后的单位阶跃响应曲线表7 混合形式传递函数双回路系统优化计算结果

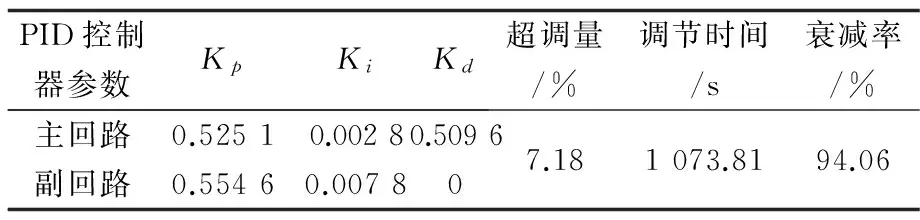
PID控制器参数KpKiKd超调量/%调节时间/s衰减率/%主回路0.52510.00280.5096副回路0.55460.007807.181073.8194.06

从图7-9以及表5-7可以看出，利用该文设计的优化软件，可以获取双回路系统的PID优化参数，并且取得了较好的优化效果。证明了软件可以有效解决双回路系统的PID控制器优化问题。

4 结束语

在简单的热工控制系统中，当被控对象的动态特性已知，PID控制器参数就会直接影响控制系统的控制品质。所以，通过对热工控制系统中的被控对象动态特性参数计算出一组最优的PID控制器参数是一项非常有实际意义的研究。针对PID单回路热工控制系统和串级热工控制系统，运用面向对象的编程语言环境，进行了这一问题的工程实现。在设计的程序中运用了粒子群优化算法(PSO)计算最优的PID控制器参数，进行了相应的控制系统仿真，并求出了控制品质参数和系统响应曲线。使用这个程序进行单回路PID控制系统和串级PID控制系统控制器的参数整定会十分方便。只要被控对象的动态特性符合n阶惯性环节加纯迟延或一阶惯性环节串联的形式，在程序界面中输入相应的数据就可以得到比较理想的PID控制器参数和仿真结果。

为了更好的解决PID参数优化这一问题，还有许多功能可以拓展，比如加入多变量的PID控制系统，这将需要解决多变量的解耦控制问题，也非常具有实际意义。另外，为了将程序作为一个整定PID控制器参数的工具使用，应该能够在运算完某一种系统的参数后，仍可以继续返回主界面进行其他系统的选择和运算。而且由于程序中只考虑到了被控对象传递函数为n阶惯性环节加纯迟延或一阶惯性环节串联这2种形式，仍有一定的局限性，可以在以后考虑添加运用有理分式表达的传递函数。

[1] 田育奇.时滞对象PID参数优化设计方法的研究[D].北京：北京化工大学，2014.

[2] 宋莉莉，朱 超，孙万麟.基于微粒群算法的PID控制器优化研究[J].昌吉学院学报，2014(6):76-80.

[3] 许骏马，侯石超，何伟光，等.遗传算法与蚁群算法在PID优化中的应用比较[J].机电信息，2013(15):114-116.

[4] 刘 明，华 亮.基于PSO算法的PID控制器参数整定[J].控制工程，2016,23(1)：64-68.

[5] 朱小明，张慧斌.PSO算法的稳定性分析及算法改进[J].计算机科学，2013，40(3)：275-278.

[6] 陈 亮，江 明，林园胜.基于PSO算法的PID控制器参数优化研究分析[J].重庆工商大学学报(自然科学版)，2014，31(5):77-80.

[7] 曾文权，余爱民.基于改进PSO算法的任务分配研究[J].计算机工程与应用，2013,49(13):51-55.

本文责任编辑：王洪娟

PID Parameters Optimization and Its Engineering Realization Based on PSO

Yao Yabin1,Wang Lijie2,Wang Jiarong3

(1. Hebei Electric Power Design&Reseach Institute,Shijiazhuang 050031,China; 2.State Grid Hebei Electric Power Research Institute,Shijiazhuang 050021,China;3.Qingdao Hongrui Power Engineering Consulting Co.,Ltd.,Qingdao 266100,China)

This paper introduces optimization method of PID controller parameters in single-loop and double-loop system by particle swarm optimization algorithm and obtains control quality parameters on the basis of digital simulation,analyze control object in form of series connection composed by n order intertial link with pure delay and first order inertia and use particle swarm optimization to find out PID parameters as well as the engineering process of corresponding simulation curve and control quality data.

PID controller;parameters optimization;parameter adjustment;PSO

2016-06-17

要亚斌(1979-)，男，高级工程师，主要从事电厂热控专业设计研究工作。

TM621

B

1001-9898(2017)03-0003-04