基于互相关函数幅值和SVM的输电塔损伤识别

霍林生， 李 旭， 李宏男, 张卓群

(1.大连理工大学建设工程学部 大连，116023) (2.国核电力规划设计研究院 北京，100095)



基于互相关函数幅值和SVM的输电塔损伤识别

霍林生1， 李 旭1， 李宏男1, 张卓群2

(1.大连理工大学建设工程学部 大连，116023) (2.国核电力规划设计研究院 北京，100095)

针对目前输电塔结构损伤识别中需要布设大量传感器的问题，提出了基于互相关函数幅值和支持向量机(support vector machine，简称SVM)的损伤识别方法。首先，定义初始与当前状态结构模态响应近似信号的互相关函数幅值差为损伤特征；其次，将损伤特征作为输入样本来训练支持向量机分类器，将损伤识别问题转化为模式分类问题；最后，利用2层角钢塔模型的振动试验，验证了方法的可行性。该方法仅需要少量传感器测得结构的动力响应，且适用于环境荷载激励，对输电塔结构损伤有较好的识别效果和噪声鲁棒性。

互相关函数； 支持向量机； 损伤识别； 输电塔

引 言

输电塔结构是输变电系统中的重要组成部分，在使用期间常年经受风荷载的作用，易导致节点螺栓松动、构件的疲劳和损伤，最终发展为整个结构体系的破坏[1]。针对输电塔结构的损伤识别，文献[2-4]分别提出了基于统计方差分析方法、小波包和模糊聚类的识别方法等，这些方法适用于输电塔结构的风荷载激励。然而，上述方法的实施均需要布置大量的传感器。

结构各点间的动力响应具有一定的相关性，发生损伤后，这种相关性将发生改变。文献[5-8]等提出了一种基于互相关函数幅值向量的损伤识别方法，利用损伤前后相邻测点互相关函数幅值的差异来识别和定位损伤，方法简单直观，易于实施。然而，其不足在于仍需要在关键点布置数量较多的传感器[9-10]。

针对上述方法的局限性，笔者提出了基于互相关函数幅值和支持向量机的损伤识别方法，该方法仅需要在关键点布置少量的传感器，且适用于任意激励。将所提出的方法应用至角钢输电塔的模型试验中，验证了其对损伤识别的有效性。

1 结构响应的互相关函数幅值

结构上各点响应的相关性用互相关函数来表示。根据自然激励法[11]，i，j两测点n阶模态的位移、速度、加速度响应的互相关函数的幅值为

(1)

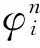
T*如式(2)所示

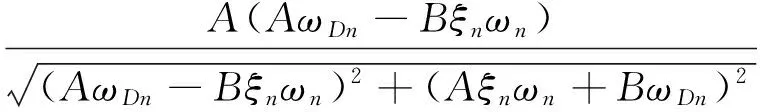
(2)

其中：A，B的取值见表1。

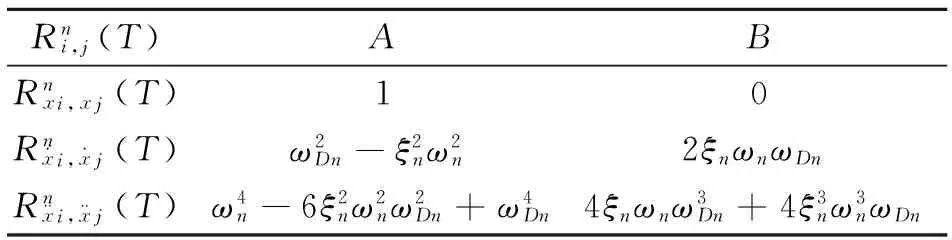
表1 A，B的取值

定义一个中间变量κ*(ξn,ωn)为

κ*(ξn,ωn)=

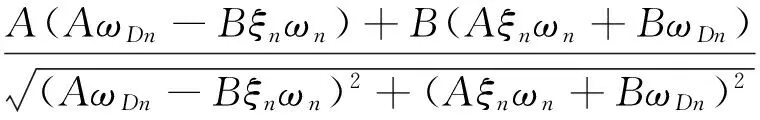
exp(-ξnωnT*)

(3)

以j点为参照点，计算其他测点与j点的n阶模态响应的互相关函数，并取其幅值组合成向量

(4)

其中：下角标CCFA表示互相关函数幅值。

由式(4)可知，结构各测点与j点n阶模态响应的互相关函数幅值向量与n阶振型密切相关。定义损伤特征为初始状态互相关函数的幅值与当前状态的差

(5)

其中：上角标intact表示初始状态；上角标current表示当前状态。

如文献[5-8]所述，在结构相应位置上布置测点，利用相邻测点DCCFA的差异来定位和评估损伤情况。然而，仅利用DCCFA进行损伤识别具有一定的局限性：首先，方法的实施需要布置数量较多的传感器；其次，方法难以在有较多相邻测点的复杂空间结构上实施。引入支持向量机等智能算法，可有效解决以上问题。

2 支持向量机SVM

SVM[12-13]是近年发展起来的、基于结构风险最小化(structural risk minimization，简称SRM)原则的统计学习算法。如图1所示，其主要思想是将数据转换到更高维的特征空间，并寻找最优分类超平面，使两种分类间的距离最大。

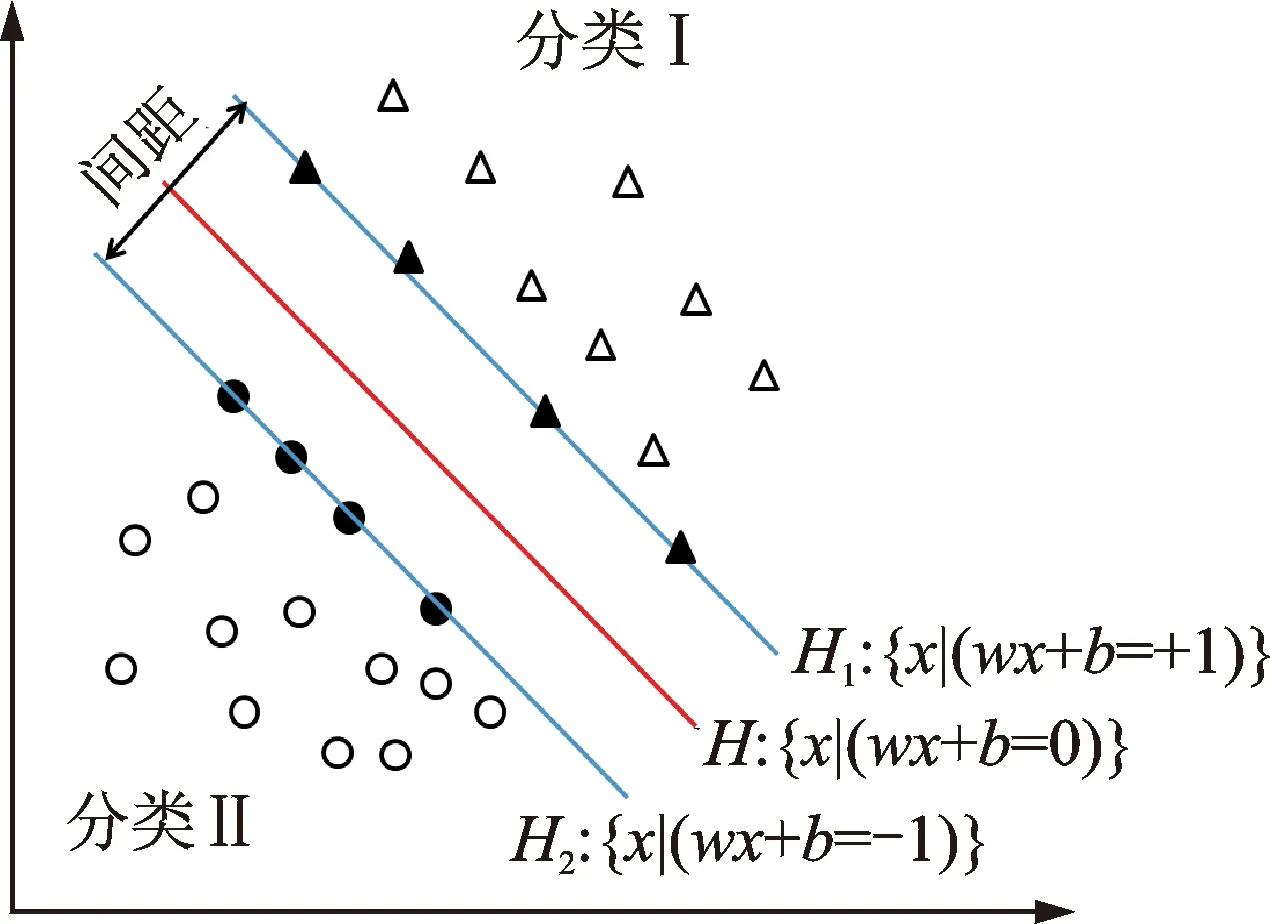
图1 支持向量机的示意图Fig.1 The diagram of SVM main idea

对于线性情况，分类超平面f(x)为

f(x)=wTx+b=0

(6)

其中：w为权值向量；b为偏置值。

其决策函数被定义为f(x)的sign函数，通过决策函数来决定输入数据的分类。

上述SVM算法适用于线性的二分类问题，对于非线性问题，可定义核函数为K(xi,xj)，决策函数变为

(7)

任何满足Mercer定理[14]的函数都可作为特征空间的核函数。常用的核函数有线性核函数、多项式核函数、径向基核函数( radial basis function，简称RBF)和S形核函数(sigmoidal kernel function，简称SKF)，其表达式见表2。

表2 常见核函数的表达式

Tab.2 Formulation of kernel functions

函数表达式线性核函数K(xi,xj)=xixj多项式核函数K(xi,xj)=(xixj+c)d径向基核函数K(xi,xj)=exp(γxi-xj2)S形核函数K(xi,xj)=tanh(γxi-xj2)

对于SVM的多分类问题，一种应用广泛的SVM的多分类策略为“一对一”(one against one，简称OAO)算法。OAO算法将构建k(k-1)/2个二分类器，其策略是：构建i，j种类的二分类问题，如果x属于第i个分类，则i分类的权重增加1；否则，j分类的权重增加1。这样x将属于权重最高的分类。OAO算法的计算简图如图2所示。

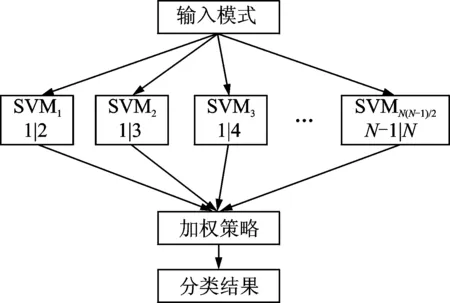
图2 OAO算法的结构图Fig.2 Structural diagram of OAO algorithm

将损伤特征作为输入样本来训练SVM分类器，以损伤形式作为输出结果，可将结构的损伤识别问题转化为模式分类问题。

3 基于互相关函数和SVM的损伤识别方法

提出了基于互相关函数幅值和SVM的损伤识别方法。由于式(4)中的VCCFA是仅与结构振型相关的向量，故激励荷载可为任意形式的荷载。如图3所示，该方法的过程如下。

1) 针对结构健康情况和每种潜在的损伤形式，采集结构的动力响应，并利用数字信号处理技术得到1阶模态响应的近似信号。

2) 选某一测点为参照点，计算与其他测点一阶模态动力响应近似信号的VCCFA。

3) 计算当前状态与初始状态VCCFA的差异，即损伤特征向量DCCFA作为训练数据，训练支持向量机分类器。

4) 采集测试样本，按步骤1～3计算测试样本的损伤特征DCCFA，并作为测试数据输入至SVM的分类器，识别结构的损伤状态。

图3 互相关函数幅值和基于SVM的损伤识别方法的过程图Fig.3 The overall procedure of cross correlation function amplitude and SVM based damage detection method

4 试验概况

以角钢塔结构模型前2层的振动试验来验证方法的有效性。试验模型是某一单回路角钢塔下2层模型，按1∶5的相似比制作。试验照片见图4。模型材料为Q235型钢材，主材为L30×4，辅材由于面积较小，利用镀锌方管线切割加工制作。为了满足模型相似度的要求，在模型顶部施加300 kg的配重。模型的前3阶频率分别为7.813，15.63，24.41 Hz。

加载设备包括2台JZK-20型激振器，以及配套的信号发生器和功率放大器。激振器一端用支架固定在反力墙上，出力端固定在试验模型的顶部，对试验模型施加水平激振力。

笔者所述方法适用于结构位移、速度和加速度响应，同样也适用于结构的应力及应变响应。采用粘贴式压电陶瓷(pb-based lanthanumdoped zirconate titanates，简称PZT)传感器来获取结构的响应信号。将PZT传感器布置在输电塔模型的一侧，布置方案见图5。其中：b1～b13为杆件编号，s1～s6为PZT传感器编号。传感器的实物照片如图6所示。用dSPACE系统采集PZT传感器的电压信号，采样频率为500 Hz。

图4 试验模型的几何尺寸Fig.4 The geometrical dimension of experimental model

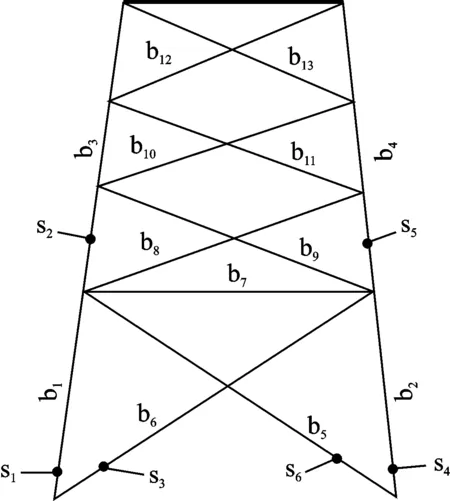
图5 杆件和传感器编号Fig.5 The numbers of members and sensors

图6 粘贴式PZT传感器Fig.6 The paste PZT sensor

节点板螺栓松动和杆件断裂是输电塔结构的两种最常见的损伤形式。其中，节点板螺栓松动属于线性结构的损伤形式，而杆件断裂常会导致结构的非线性损伤。所有损伤工况如表3所示。其中：工况2～5是通过将节点板上的螺栓松动来模拟线性结构的损伤，工况5中出现损伤的b7杆上并未布置传感器；工况6为输电塔模型b5另一侧的一柱脚完全断裂，用于模仿结构非线性的损伤，且损伤位置远离所有传感器。

5 结果分析

输电塔结构在服役过程中，所经受的环境荷载主要包括风荷载，频率范围通常在30 Hz范围内[15]。对结构施加频率范围为0～30 Hz的高斯白噪声激励，采样时间为20 s。当结构的响应进入平稳状态后，开始采集传感器信号。采集40组无损伤工况，即工况1的PZT传感器信号，将其中的20组作为初始状态的样本，其余20组作为当前状态无损情况的样本。对于损伤工况，即工况2～工况6，分别采集20组PZT传感器信号作为当前状态损伤情况的样本。利用笔者提出的方法来识别输电塔结构的损伤情况。

表3 输电塔损伤工况

选择db25小波基，对传感器响应进行4层小波包分解，对包含1阶频率的小波包尺度信号进行重构叠加，作为1阶模态响应的近似信号。PZT传感器的信号，以及用小波包技术得到的1阶模态响应的近似信号如图7所示。可以看出，结构响应和经小波包提取的1阶模态响应在第1阶频率处的幅值几乎相等，可以认为已将1阶模态响应近似的提取出来。

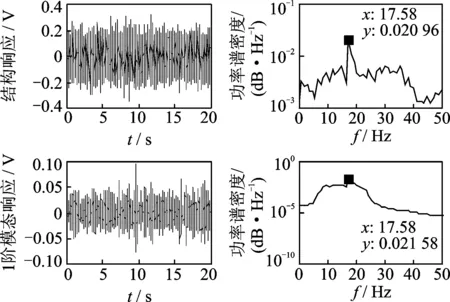
图7 PZT传感器信号以及1阶模态响应的近似信号Fig.7 The dynamic response of PZT sensor and the 1st modal response

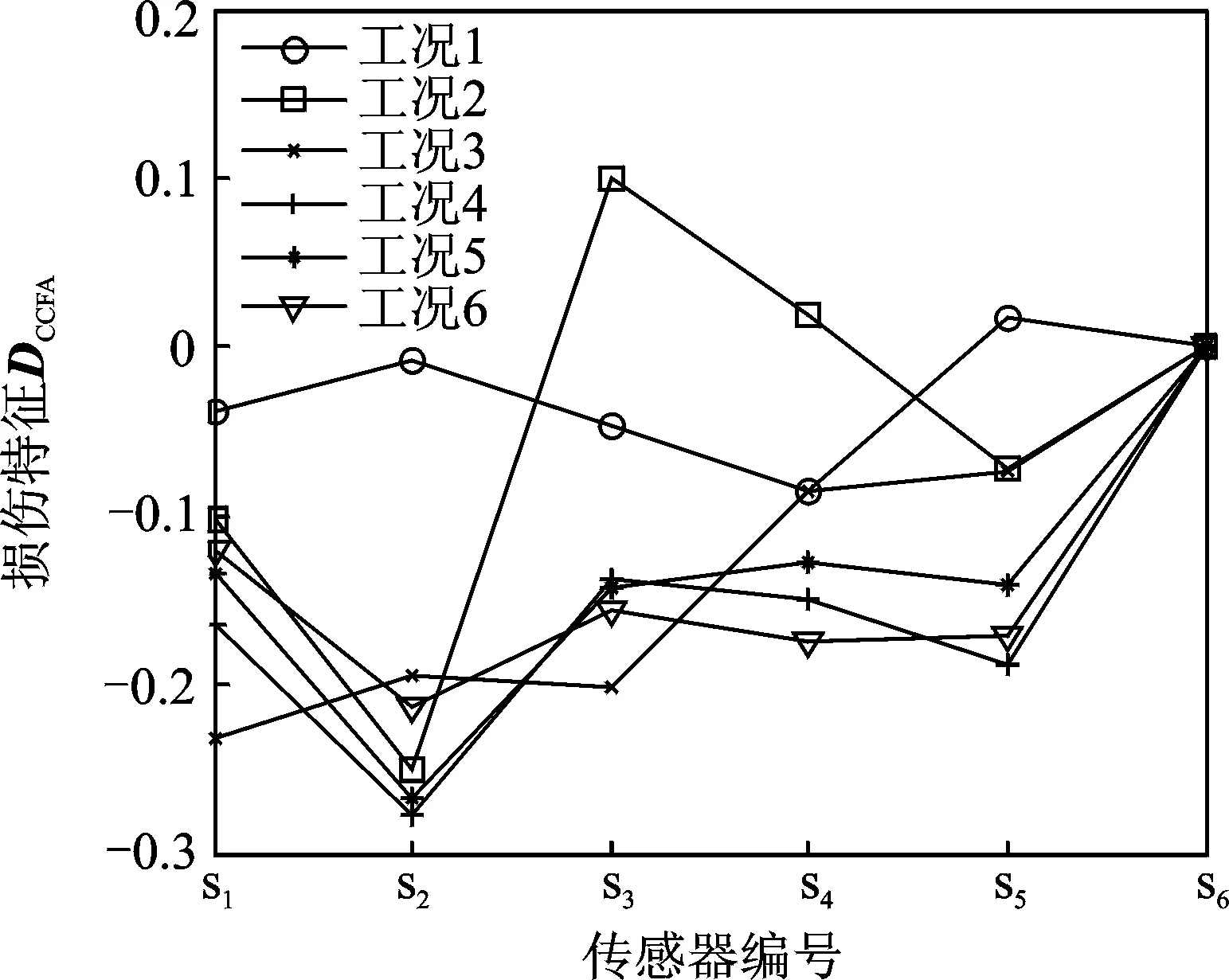
图8 不同工况下的损伤特征Fig.8 The DCCFAfrom different damage patterns

笔者利用Libsvm工具箱[16]来完成支持向量机的训练和分类工作，分别利用了多项式核函数(d值取3)、RBF核函数和SKF核函数。利用格点搜索方法获取参数C与γ的最优组合，如图9所示。每种工况识别结果的正确率如表4所示。其中，以RBF函数为核函数的平均正确率为95%。可以看出，笔者所述的方法能较好地识别出输电塔结构的各种程度损伤情况。

表4 输电塔损伤识别结果的正确率

笔者还对比分析了几种目前常用于输电塔结构损伤识别的损伤特征的识别能力，分别为小波包能量谱和统计方差。为了进一步分析方法的抗噪能力，在输电塔响应上施加噪声水平均值为20%的白噪声，识别结果如图10所示。其中： “小波包”表示以小波包能量谱作为损伤指标；“统计方差”表示以统计方差作为损伤指标。可以看出，相比较而言，笔者所述方法具有更好的噪声鲁棒性，在额外施加20%的噪声情况下，有更好的识别能力。

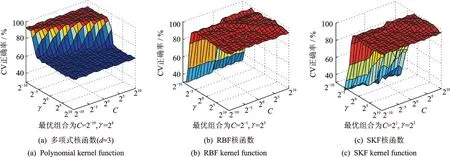
图9 交叉验证(CV)准确率随参数的分布以及C和γ的最优组合Fig.9 The CV accuracy with C and γ and the best combination of C and γ

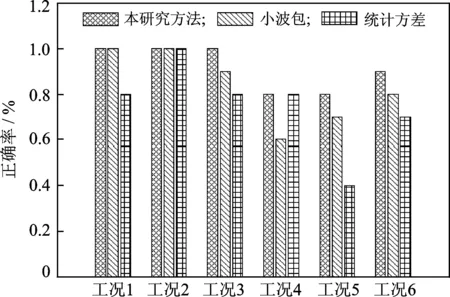
图10 不同损伤指标的识别结果Fig.10 The classification results with different damage features

6 结 论

1) 通过结合互相关函数幅值与支持向量机，将结构的损伤识别问题转化为分类问题，可有效解决互相关函数幅值方法须布置数量较多传感器和不宜用于复杂空间结构的问题。

2) 笔者采用的损伤指标是仅与结构振型相关的向量，与荷载形式无关，故所提出的方法可用于环境荷载激励。

3) 从输电塔模型试验可以看出，笔者所述方法可有效识别输电塔结构损伤形式，且有较好的噪声鲁棒性。

[1] 李宏男，白海峰. 高压输电塔-线体系抗灾研究的现状与发展趋势[J].土木工程学报，2007,40(2):39-46.

Li Hongnan, Bai Haifeng. State-of-the-art review on studies of disater resistance of high-voltage transmission tower-linesystems[J]. China Civil Engineering Journal, 2007,40(2):39-46.(in Chinese)

[2] 秦文科. 钢管输电塔法兰联结结点螺栓脱落损伤诊断的研究[D]. 武汉：武汉理工大学， 2008.

[3] 谭冬梅，秦文科. 基于统计的小波包分析的输电塔结构损伤预警[J]. 地震工程与工程振动，2010,30(4): 115-120.

Tan Dongmei, Qin Wenke. Damage pre-warning of transmission tower based on statistical wavelet packet analysis[J]. Journal of Earthquake Engineering and Engineering Vibration，2010,30(4): 115-120.(in Chinese)

[4] 谭冬梅，瞿伟廉，秦文科. 基于小波包和模糊聚类的输电塔结构损伤诊断[J]. 天津大学学报, 2011, 44(8): 695-700.

Tan Dongmei, Qu Weilian, Qin Wenke. Damage identification of transmission tower based on wavelet packet transform and fuzzy clustering[J]. Journal of Tianjin University, 2011, 44(8): 695-700. (in Chinese)

[5] Yang Zhichun, Wang Le, Wang Hui, et al. Damage detection in composite structures using vibration response under stochastic excitation[J]. Journal of Sound and Vibration, 2009, 325(4): 755-768.

[6] Yang Zhichun, Yu Zhefeng, Sun Hao. On the cross correlation function amplitude vector and its application to structural damage detection[J]. Mechanical Systems and Signal Processing, 2007,21(7): 2918-2932.

[7] Wang Le, Yang Zhichun, Waters T. Structural damage detection using cross correlation functions of vibration response[J]. Journal of Sound and Vibration, 2010,329(24): 5070-5086.

[8] Wang Le, Yang Zhichun. Effect of response type and excitation frequency range on the structural damage detection ethod using correlation functions of vibration responses[J]. Journal of Sound and Vibration, 2013,332(4): 645-653.

[9] Hera A, Hou Zhikun. Application of wavelet approach for ASCE structural health monitoring benchmark studies[J]. Journal of Engineering Mechanics, 2004, 130(1): 96-104.

[10]Yang J N, Lei Ying, Lin Silian, et al. Hilbert-Huang based approach for structural damage detection[J]. Journal of Engineering Mechanics, 2004, 130(1): 85-95.

[11]Farrar C, James III G. System identification from ambient vibration measurements on a bridge[J]. Journal of Sound and Vibration, 1997, 205(1): 1-18.

[12]Widodo A, Yang B S. Support vector machine in machine condition monitoring and fault diagnosis[J]. Mechanical Systems and Signal Processing, 2007, 21(6): 2560-2574.

[13]鞠华,沈长青,黄伟国，等. 基于支持向量回归的轴承故障定量诊断应用[J].振动、测试与诊断, 2014, 34(4): 767-771.

Ju Hua, Shen Changqing ,Huang Weiguo, et al. Quantitative diagnosis of bearing fault based on support vector regression[J]. Journal of Vibration, Measurement & Diagnosis, 2014, 34(4): 767-771. (in Chinese)

[14]Vapnik V N. The nature of statistical learning theory[M]. New York: Springer, 1999:123-180.

[15]白海峰, 李宏男. 大跨越输电塔线体系随机脉动风场模拟研究[J]. 工程力学, 2007, 24(7): 146-151.

Bai Haifeng, Li Hongnan. Simulation study of stochastic fluctuating wind field on large span elatricity transmission tower-line system[J]. Engineering Mechanics, 2007, 24(7): 146-151.(in Chinese)

[16]Zeng Min, Lin Lei, Cheng Wenming. Research of regional freight volume forecasting based on LIBSVM and time series[J]. Computer Engineering and Applications, 2013, 49(21): 6-10.

10.16450/j.cnki.issn.1004-6801.2017.03.012

国家基础研究发展计划(“九七三”)计划资助项目(2015CB057704)；国家自然科学基金创新群体资助项目(51421064)；大连市建设科技计划资助项目

2015-04-13；

2015-11-27

TU391

霍林生，男，1975年5月生，副教授。主要研究方向为建筑结构抗震、控制及监测。曾发表《Semi-active vibration suppression of a space truss structure using a fault tolerant controller》(《Journal of Vibration and Control》2012,Vol.18,No.10)等论文。 E-mail: lshuo@dlut.edu.cn