光纤光栅传感网络的冲击定位方法

2017-07-01王景霖何召华梁大开单添敏林泽力

振动、测试与诊断 2017年3期

曹亮，王景霖，何召华，梁大开，单添敏，林泽力

(1.上海航空测控技术研究所故障诊断与健康管理技术航空科技重点实验室上海，201601)(2.南京航空航天大学机械结构力学及控制国家重点实验室南京，210016)

光纤光栅传感网络的冲击定位方法

曹亮1，王景霖1，何召华1，梁大开2，单添敏1，林泽力1

针对航空航天层合板结构冲击与振动监测的需求，提出一种基于小波包分解方法和分布式光纤光栅传感网络的板状结构低速冲击辨识方法。根据四边固支板结构的承载形式与光纤光栅传感器的感知特性，设计合理的传感器网络布局，再利用快速傅里叶变换(fast Fourier transformation，简称FFT)与小波包分解对光纤光栅传感网络监测到的冲击响应信号进行时频域分析，获取能表征冲击特性的时域特征分解信号。在此基础上，分别计算出每一个特征分解信号与其对应的时域原始信号之间的互相关系数，并将其做为相似度分配权值，分解出所有样本冲击点对应冲击响应信号的特征分解信号，构建样本信息库。利用Haudorff距离计算测试信号与样本信息库各个信号之间的相似度，并根据相似度来确定冲击点的位置坐标。研究表明，该方法能够实现对航空航天层合板结构低速冲击位置的辨识。

光纤光栅传感网络；层合板；小波包分解；冲击定位

引言

现代航空业的快速发展，对航空航天飞行器结构的性能提出了更高要求，其主要体现在针对结构材料性能的提高，如要求更高的结构强度、刚度以及抗腐蚀能力和抗电磁干扰能力。层合板由于具有高比强度、良好的抗疲劳性、耐腐蚀性以及绝缘、热导率低等优点[1]，在航空航天领域得到了快速发展和广泛应用。然而层合板结构在制作和使用过程中易受环境因素以及材料属性变化的影响，尤其是在层合板结构使用过程中受到振动冲击作用产生隐蔽性的损伤[2]，造成层间脱层、纤维断裂以及内部产生裂纹等现象。隐形损伤在一定程度上降低了层合板的使用可靠性，并造成不可估量的安全隐患。因此，对层合板结构的冲击定位问题的研究是非常必要的。

光纤光栅传感器具有芯径细、质量轻、柔韧性好的优点，适合于与柔性充气结构一体化集成，同时又耐腐蚀，抗电磁干扰能力强[3-4]，因此，在基于光纤光栅传感器的复合材料冲击定位研究领域也得到了应用。Kuang等[5]将光纤光栅传感器埋入先进航空复合材料中用于监测其性能及损伤状态，当栅区处在非均匀应变场或者受到局部不对称加载状态下，光纤光栅传感器的光谱分裂成对个波峰，因此，可根据此原理研究加载事件过程中的应变异常现象。杨智春等[6]利用小波系数差的模实现了对复合材料悬臂梁的损伤定位。陆观[7]利用分布式光纤光栅传感网络监测板状复合材料的冲击状态，并利用黄氏变换以及自回归模型系数来实现对冲击响应信号的特征提取，并通过马氏距离的相似度判别来实现冲击位置的辨识。

笔者在对光纤光栅传感特性以及网络优化布局研究的基础上，利用分布式光纤光栅传感网络实现对板状复合材料结构的冲击位置辨识。

1 冲击定位原理

1.1 光纤光栅传感原理

光纤布拉格光栅作为一种反射型光纤传感器，仅反射特定波长附近的窄带光波。当宽带光源输入光纤光栅传感器栅区，特定波长的光波满足了栅区反射条件，并发生反射，如图1所示。当光栅栅区不受力时，其传感原理[8]为

λ=2nΛ

(1)

其中：λ为光纤光栅反射光谱中心波长；n为纤芯有效折射率；Λ为光栅周期。

图1 光纤光栅传感器原理Fig.1 The principle of fiber grating sensor

由式(1)有

Δλ=2ΛΔn+2nΔΛ

(2)

当光纤布拉格传感器受到应变场和温度场变化影响时，反射光谱中心波长λ会发生偏移。光栅在只受应力的作用时，光栅栅区周期、有效折射率与栅区所受动态应变关系[8]为

(3)

光栅在仅受温度场作用时，其有效折射率及应变同温度T之间关系如下

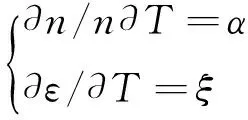
(4)

其中：ε为光栅栅区应变；Pe为光弹系数(纤芯材质确定时为常数)；α为热膨胀系数；ξ为热光系数；ΔT为环境温度变化量。

根据式(2)、式(3)和式(4)，可得中心波长偏移量Δλ与动态应变ε及温度变化量ΔT之间的关系[9]为

Δλ=λ[(1-Pe)ε+(α+ξ)ΔT]

(5)

由式(5)可知，栅区应变及温度对栅区中心波长偏移量Δλ的影响可进行叠加，因此应变对栅区中心波长的影响与温度变化对栅区中心波长的影响是相互独立的。

1.2 小波包分解

函数ψ(x)的傅里叶变换ψ(ω)满足容许性条件[10]

(6)

该函可作为一个基本小波母函数，通过变化小波母函数的尺度因子，可在时域尺度上进行伸缩和平移。时域尺度上平移伸缩后的函数为φ(m,n)(x)，其变换因子为m，平移因子为n，则有[7]

(7)

小波包与小波分析相同，也是由一系列线性组合的小波函数φi(x)组成，即

(x)=2j/2φi(2jx-k) (i=1,2,3…)

(8)

其中：i,j,k分别为频率因子、尺度因子和平移因子。

小波包在使用过程中同样表现出正交性、时频性等性质，与相应的小波函数相似。

由于复合材料板具有各向异性的特质，造成冲击响应信号频率成分复杂，因此需要分析不同频率成分与冲击位置之间的对应关系，以表征冲击响应信号的特征。小波包分解方法具有不同尺度的小波母函数，能够根据信号特征频率选择相应的频带，提高时频分辨率[11]。小波包分解对各层各阶信号的频段划分公式为

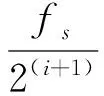
(9)

其中：n为层数；i为阶数；fs为采样频率。

因此，可以根据固有频段范围来计算小波包分解所需要的层数和阶数。

1.3 向量相关性评定

每一个光纤光栅传感器监测到的冲击响应信号经小波包分解后能得到特征分解信号，将特征分解信号与其对应的原始信号之间的互相关系数作为对应传感信号之间H距离值的分配权重系数，记为α1,α2,…，αn。互相关系数的求解过程如下：已知两向量a和b，把a向量作为行向量，b向量作为列向量，则向量a，b之间的互相关系数[12]为

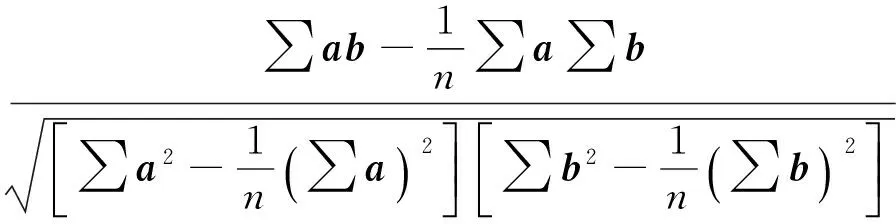
(10)

1.4 Hausdorff距离

Hausdorff距离是描述两组点集之间相似度的一种量。它是两种点集之间的一种定义形式：假设有两组集合A=[x1,x2,…,xm]，B=[y1,y2,…,yn]，则两集合之间的Hausdorff距离定义为

H(A,B)=max[h(A,B),h(B,A)]

(11)

其中：h(A,B)，h(B,A)为

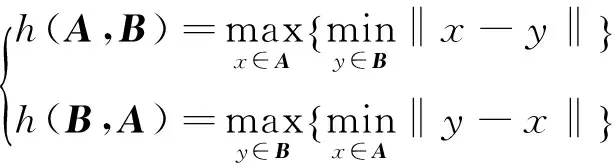
(12)

h(A,B)指每个点ai到距离此点最近的B集合中的点bj之间的距离‖ai-bj‖进行排序，取其最大值作为h(A,B)的值，同理h(B,A)。

H(A,B)取h(A,B)，h(B,A)中的较大值，度量两个点集之间的最大不匹配程度。

2 冲击实验系统

图2所示为冲击实验系统实物图。基于分布式光纤光栅传感网络的冲击定位系统分为传感系统、数据采集与传输系统及数据处理和评估系统。其中：传感系统由级联而成的光纤光栅传感网络组成，监测板面的冲击状态；数据采集与传输系统由计算机和光纤光栅解调仪组成，用以采集和保存冲击响应信号；评估系统为相关定位程序，用以实现对冲击位置的辨识。

层合板板面有效面积为540 mm×540 mm。为方便确定冲击点位置以及精确加载，取板面中心位置、大小为300 mm×300 mm的区域作为冲击监测区域，并划分成规则的11行、11列共计121个点的网络，网格划分形式如图3所示。

图2 冲击实验系统Fig.2 The diagram of impact test system

在冲击监测区域的四周布置由4个光纤光栅传感器(fiber bragg grating，简称FBG)组成的光纤光栅传感网络，各传感器的分布位置、中心波长以及分布形式如表1和图3所示。

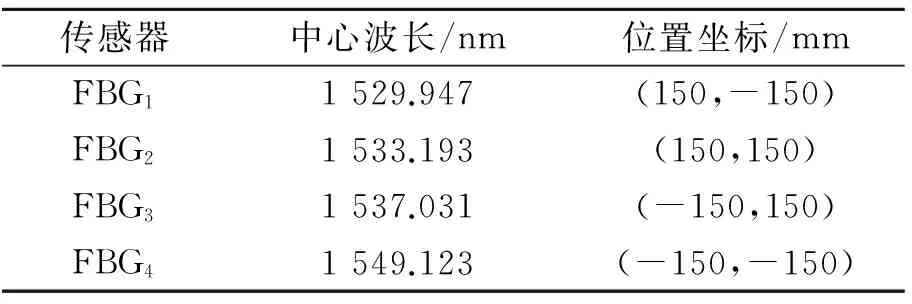
表1 FBG传感器中心波长与位置

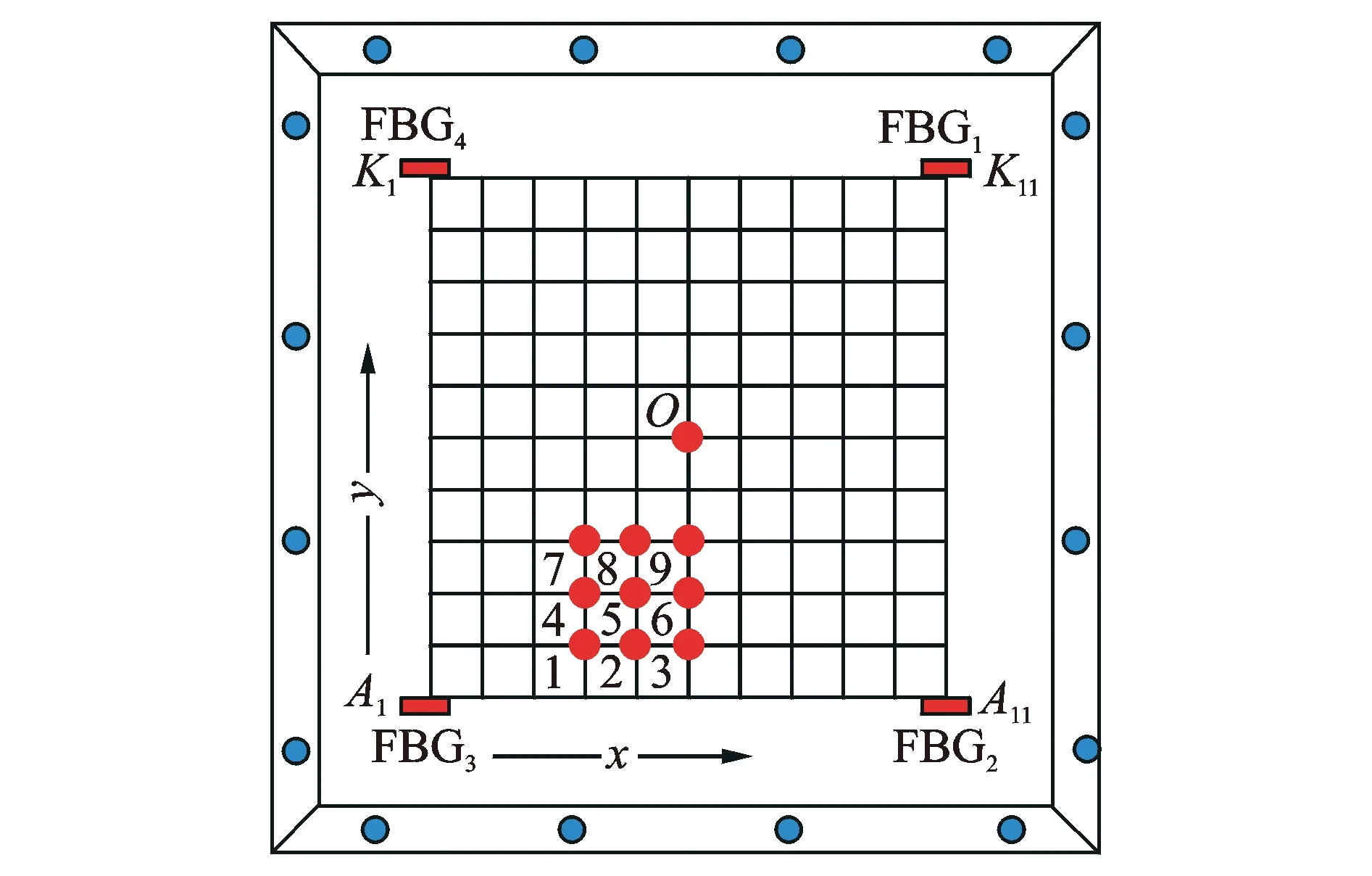
图3 板面网络划分形式及传感器布局图Fig.3 The diagram of plank′s network and sensors′ location

3 冲击实验结果与分析

利用上述冲击实验系统，监测层合板面冲击状态，并实现冲击载荷的定位辨识。

3.1 频谱分析

对板面中心位置施加冲击载荷，研究光纤光栅传感网络中各传感器所监测到的冲击响应信号。如图3所示，采集并处理冲击点O(0 mm,0 mm)处相应的冲击信号。图4所示为O点的冲击响应信号时频域分析图，由上到下分别为光纤光栅传感器FBG1，FBG2，FBG3与FBG4对应的时频图谱。

图4(a)为施加冲击载荷状态下不同传感器监测到的时域响应信号。冲击点距离各传感器的传感距离相同，但其相应的中心波长偏移量不同，均不超过200 pm，持续时间不超过0.3 s。同时冲击中心位置里各个固支边较远，固支边对其影响较小，因此各传感器监测的波长偏移不会出现较大的波动。波长偏移量对应关系为：ΔλFBG3>ΔλFBG4>ΔλFBG2>ΔλFBG1，这是因为树脂复合材料在材料性能上表现为各向异性，因此也造成排布方向相同的传感器的中心波长偏移量不相同。图4(b)为冲击响应传感信号的傅里叶变换频谱图，从图中可以看出，冲击响应信号中的敏感频率为70,110,150和200 Hz，其中以70 Hz左右的频段范围为主，且幅值最大。因此，可断定该层合板冲击响应信号的特征频率为70 Hz。

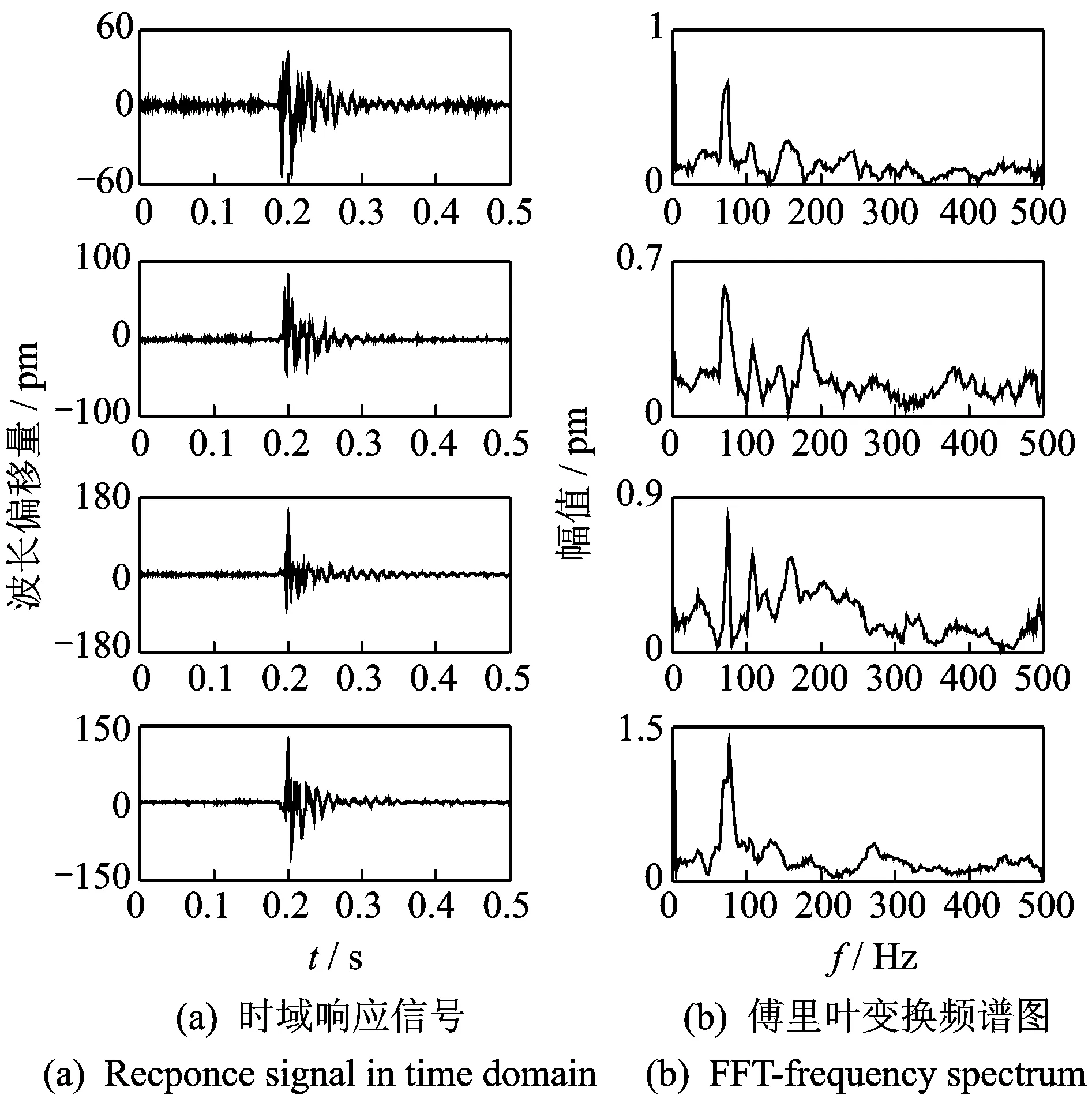
图4 传感网络冲击响应信号时频图Fig.4 The frequency diagram to the impulse response signal of sensor network

3.2 小波包分解及互相关系数的计算

根据确定的冲击响应信号特征频率，对上述冲击响应信号进行小波包分解处理，如图5所示。其中图5(a)为冲击过程中4个FBG传感器监测到的原始信号，图5(b)为对该信号监测到的原始信号进行小波包分解，获取包含特征频率的的特征分解信号。

对小波包分解获得的特征分解信号进行频谱分析，如图6所示。其特征频段范围为45～85 Hz，其中最大频谱值为70 Hz左右，与小波包分析所得结果基本一致。

3.3 数据库建立及信息比对

如图7所示，选取图中标记数码的9个冲击点为样本点，按照标记数码的大小顺序依次对上述样本点进行等能量冲击，记录并保存所有样本点的冲击响应信号S，获取各冲击响应信号对应的特征分解信号s，并计算其相应的互相关系数。

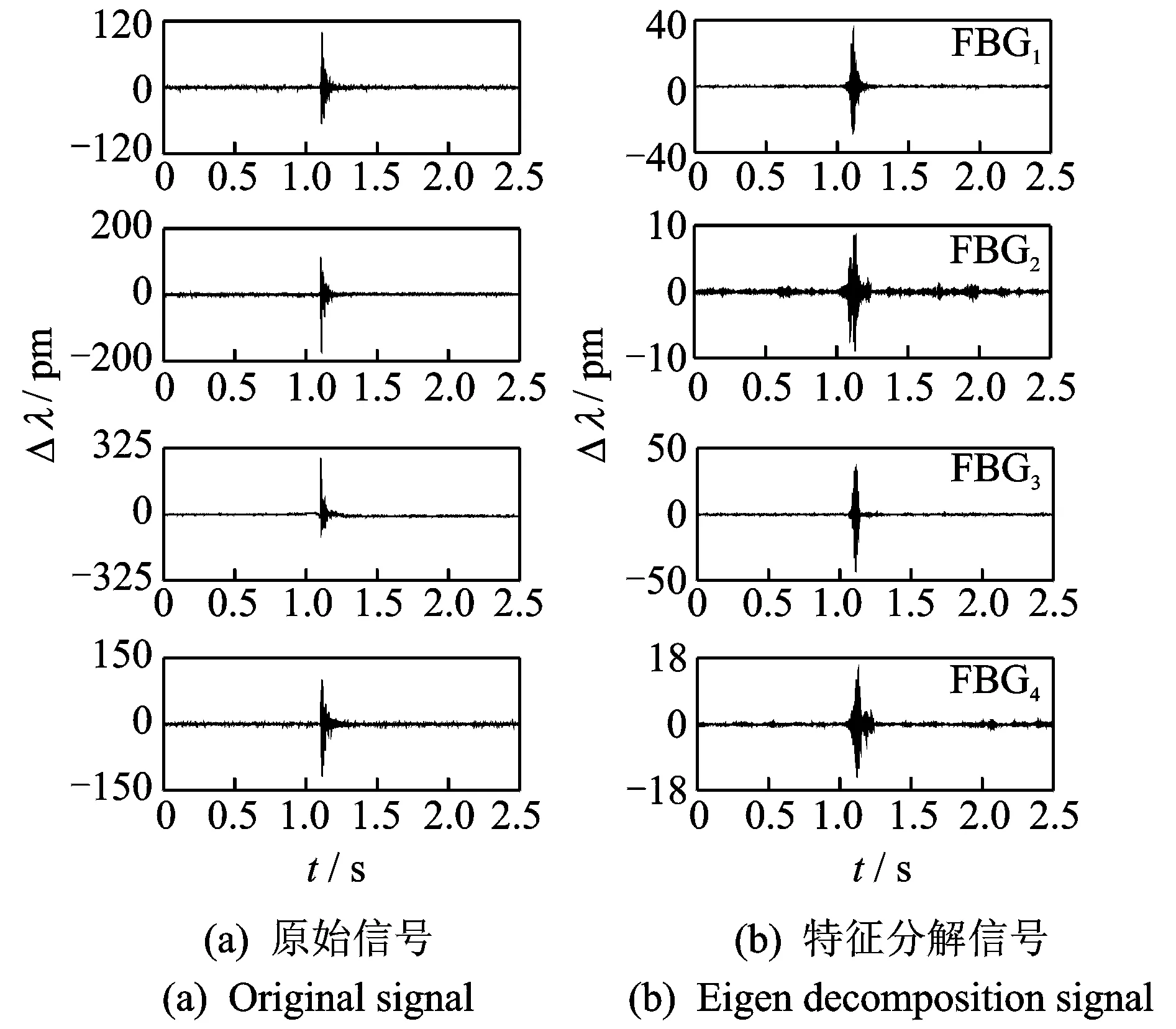
图5 冲击响应信号对应的小波包分解信号Fig.5 The wavelet packet decomposition signal of the shock response signal

图6 小波包分解信号频谱图Fig.6 Frequency spectrum of the wavelet packet decomposition signal

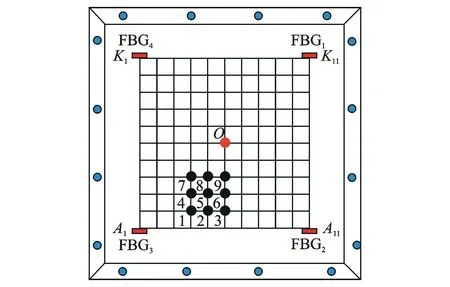
图7 样本点位置示意图Fig.7 Sketch diagram of sample points

每一个冲击点对应4个冲击响应信号(光纤光栅传感网络包含4个FBG传感器)，每一个冲击响应信号对应一个特征分解信号si，因此，每个冲击点对应4个特征分解信号si1，si2，si3和si4。将此4个特征分解信号按传感器排列顺序组建一个二维矩阵，则9个样本点对应9个二维矩阵，这些二维矩阵共同构成了样本点的特征信息数据库。

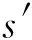
Hi=αi1Hi1+αi2Hi2+αi3Hi3+αi4Hi4

(13)

根据分析，分别对上述9个样本点冲击一次，获取9组测试信号，按照信号分析流程分别求取9个测试点与样本库中特征信息库矩阵之间的综合H距离值，其结果如图8所示。

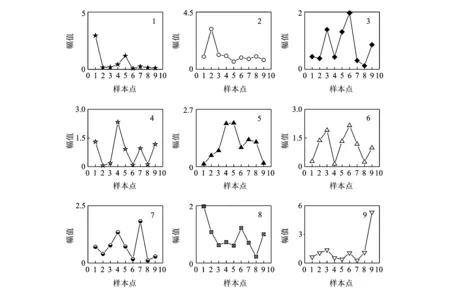
图8 测试点综合H距离值分布图Fig.8 The distribution of H distance to the sample points

由图8可知，仅有3号、8号测试点未能准确判别出结果，其他测试点均能实现定位辨识。

4 结论

1) 结合光纤光栅传感器的传感特性，优化FBG传感器的布局，以实现对板面监测范围的最大化。

2) 利用小波包对信号处理过程中体现出的自适应性，提高了对信号时频域分析的能力，并获取了能表征信号特征的时频域信息。

3) 采用集合之间相似度比对的方法，并利用Hausordff距离作为衡量集合之间相似度的指标，提高其辨识能力。

[1] 陈浩然,刘远东.动荷载作用下含损伤复合材料层合板承载能力[J].复合材料学报，2004，21(3)：115-119.

Chen Haoran, Liu Yuandong. Loaded capability of delaminated composite plates under dynamic loading[J]. Acta Materiae Compositae Sinica, 2004，21(3)：115-119. (in Chinese)

[2] 陆观，梁大开，曾捷，等. 基于光纤光栅传感器的复合材料层合板冲击能量研究[J].振动与冲击，2011，30(6)：261-264.

Lu Guan，Liang Dakai, Zeng Jie, et al. Impact energy on composite material layer based on grating sensors[J]. Journal of Vibration and Shock, 2011，30(6)：261-264. (in Chinese)

[3] 贾子光,任亮,李宏男,等.应用光纤光栅传感器[J].中国激光，2010，37(5)：1298-1303.

Jia Ziguang, Ren Liang, Li Hongnan, et al. Application of fiber bragg grating sensors in monitoring curing process of carbon fiber composite[J]. Chinese Journal of Lasers,2010,37(5):1298-1303. (in Chinese)

[4] 王义平，唐剑，尹国路，等. 光纤光栅制作方法及传感应用[J].振动、测试与诊断，2015，35(5)：809-819.

Wang Yiping, Tang Jian,Yin Guolu,et al.The fabrication method and sensing application of fiber grating[J]. Journal of Vibration, Measurement & Diagnosis, 2015，35(5)：809-819. (in Chinese)

[5] Kuanga K S C, Kennyb R, Whelan M P, et al. Embedded fiber Bragg grating sensors in advanced composite materials[J]. Composites Science and Technology, 2001(61):1379-1387.

[6] 杨智春，党晓娟，王乐，等.复合材料结构损伤联合定位法试验研究[J].振动、测试与诊断，2010，30(2)：115-118.

Yang Zhichun, Dang Xiaojuan, Wang Le, et al. Experimental investigation on a combined damage localization method for composite beams and plates[J]. Journal of Vibration, Measurement & Diagnosis, 2010，30(2)：115-118. (in Chinese)

[7] 陆观.光纤Bragg光栅在智能材料结构健康监测中的应用研究[D].南京：南京航空航天大学，2011.

[8] 张威,梁大开,芦吉云,等.光纤光栅传感系统信号解调技术的研究[J].压电与声光,2008,30(6)：677-679.

Zhang Wei, Liang Dakai, Lu Jiyun,et al. Research on demodulating technique for fiber grating seansor system[J]. Piezoelectectrics & Acoustooptics, 2008,30(6)：677-679. (in Chinese)

[9] Zubia J, Mateo J, Losada M A, et al. Optical fiber sensors for structural health monitoring in airplanes[C]∥15th International Conference on Transparent Optical Networks. Poland: Journal of Telecommunications and Information Technology, 2013.

[10]汪富泉,李厚强.小波理论与分形[J].物理,1994,23(9):539-543.

Wang Fuquan, Li Houqiang. Wavelet and fractal theory [J]. Physics,1994,23(9):539-543. (in Chinese)

[11]刘守山,杨辰龙,李凌,等.基于自适应小波阈值的超声信号消噪[J].浙江大学学报,2007,41(9):1557-1560.

Liu Shoushan, Yang Chenlong, Li Ling, et al. Adaptive wavelet thresholding based ultrasonic signal denoising[J].Journal of Zhejiang University, 2007,41(9):1557 -1560. (in Chinese)

[12]王正林,龚纯,何倩.精通Matlab科学计算[M].北京:电子工业出版社,2007:54-55.