化归思想在高中数学解题中的应用分析
2017-06-30莫京宇
莫京宇
摘要:数学对于高中课程当中尤为重要,学习数学的关键在于对数学知识的掌握和拥有良好且正确的解题思想。在数学解题应用中,如等价交换思想、数形结合思想、函数思想等这些良好的解题思想我们都可以称之为化归思想。本文就化归思想在高中数学解题中的实际应用作出简要分析。
关键词:化归思想;高中数学;应用
前言:化归思想,一种化熟悉为陌生,化未知为己知的思想。这种思想在生活中被我们习惯性地应用着,一个人的成长离不开化归思想,它是我们思考一切问题的基本习惯。同样,在高中数学领域也离不开化归思想,关于它在高中数学解题中的应用,我认为可以分为五个方面进行,即在不等式中的应用,在数列中的应用,在函数中的应用和在几何中的应用。
一、化不等式为等式
化归思想在不等式当中的应用表现最为明显的是化不等式为等式。因为等号两端的数值相同,根据这一点我们可以进行具体的运算,进而得出答案。举个例子:题目为若不等式kx-4=2的解集是x1≤x≤3,则实数k是多少。
通过观察题目可以解析出kx-4=2的两个根为1,3 即k-4=23k-4=2 ,可以解得k=2。在这个问题中,我们利用化归思想将端点之进行带入,在等号成立的情况下将题解开。在所有高中数学的不等式的问题之中,只要我们能够找到不等式之间的关系,将不等式转化为等式,问题就都能够被解开[1]。
二、转化为等差数列或等比数列
数列是高中数学学习当中的重点,同时也是高考数学的必考内容。同样,化归思想在高中数学数列题型当中也有很好的應用,主要是根据题目内容将其转化为等差数列或等比数列,然后利用所学习的公式求得答案[2]。
1.在等差数列当中的应用
在高中数学的等差数列习题当中,经常出现的像an-an-1=fn这种等差数列的递推公式,我们通常可以利用叠加方法来进行解题。举个例子。题目为已知an-an-1=n-1,求an。根据题目可知,an-an-1=n-1,所以我们可以推断出a2-a1=1,a3-a2=2,a4-a3=3……所以我们利用叠加法将各项相加,可以得到an-an-1=1+2+3+4+...+n-1,进而可以推算出结果,即an=n2-n+22。
叠加法进行解题时我们可以用它的两个特点进行观察,第一个特点是等式的右方求和要更快捷,第二个特点是等式的左方可以错项互相消掉,从而变成简单的公式。这种方法的应用也正是化归思想的数学解题中应用中常见的证明。
2.在等比数列当中的应用
在等比数列当中我们也会使用到化归思想,由于化归思想而采用的方法在等比数列当中有累乘法、迭乘法等等。对于题目上有像anan-1=fn这样的公式,我们能够通过后者进行求解。比如这样的一道题:已知数列a1=1,anan-1=nn+1求数列an的通项公式。通过观察,我们可以推导出a2a1=23,a3a2=34……一直到anan-1=nn+1,将上面的所有等式相乘可以算出ana1=2n+1,进而我可以得出an=2n+1。在这道题中,我们通过利用化归思想的迭乘法算出了anan-1=fn类型的等比数列通项公式,当然它也具有一定的要求,即:通过跌乘之后得出的f1f2……fn公式可以进行化简。
三、数形转化与动静转化
函数一直都是高中数学学习的重点,其中涵盖了一次函数、二次函数、反比例函数等一共七个基本的初等函数,同样,这也是高考必须涉及的范围[3]。化归思想在解函数题型当中的运用主要为数形之间的转化和动静之间的转化。
1.数形之间的转化
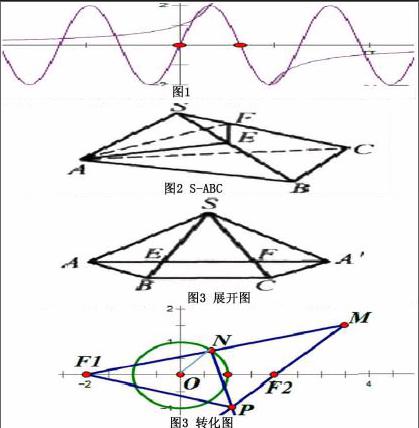
在一部分函数题中,数字和图形总是互相结合的,我们通过数字和图形之间的转化能够让函数题变得更加简单,从而解出答案。比如有这么一道题:函数y=11-x的图像和函数y=2sinπx,-2≤x≤4的图像的所有焦点的横坐标之和为多少。这是一道选择题,有四个选项,分别为2,6,8,10。这道题需要我们进行函数和图像的结合去进行解题。我们需要作出函数y=11-x与函数y=2sinπx,-2≤x≤4的图像,如图1所示。
通过对图像的观察,我们可以知道那两个函数图像都是关于(1,0)这个点对称的,所以相交的点也就是关于这个点对称的。而再看图像,我们还可以观察到这图像当中,在y=11-x,y=2sinπx,-2≤x≤4函数图像在区间(-2,4)里面存在了8个相交的点。所以根据公式,我们可以算出横坐标是答案C,有8个。这道题就是利用了数字和图形之间的转换,将一个乍看很复杂的题变得简单了。
2.动静之间的转化
动静之间的转化指的是我们在解函数题时,利用变化与运动的思路去分析题目,去将题目中有用的信息利用函数的形式进行表现,去将静止的数字变成变量,实现动静之间的相互转化,进而解决问题,这在高中函数题中同样常见,比如这样的一道题:20001999和19992000哪个数值更大?第一眼看起来这两个数字都很大,通过目测看不出来谁打谁小,好像无法进行比较。不过我们通过动静转化可以慢慢得出答案,第一步转化为对数和指数,假设ab>ba,那么我们现在把参数相同的转化为不等式的一端,在两端都取自然的对数,可以算出blna>alnb,lnaa>lnbb。这是我们在静态和静态之间的转化,也是第一步的转化,接下来进行第二步,通过构成公式y=lnxx(x>1),然后把a与b当作是这个公式的自变量,通过计算我们便可以进行比较看看20001999和19992000这两个数值的哪一方数值更大了。
四、化归思想在几何中的应用
几何也是高中数学的重要组成部分,化归思想同样在几何中多有应用,具体可以分为立体几何和解析几何。
1.高维转化低维
立体几何都是三维的,在直接运算上很困难,这时我们需要将题目中的立体几何转化为二维的平面图形,然后再进行运算,比如图二中的立体图形,题目给定条件为这是一个正三棱锥S-ABC,它的底边长度是a,而侧棱长是2a,现在过A点作与侧棱SB、SC全部相交的AEF截面。求该面的最小周长。
在解决这道问题时,我们需要利用化归思想。周长的距离可以转化为点与点之间的线长问题,所以我要要将沿着SA把这个三维立体的侧面打开,得到图3,进而只求A和A′之间的最短距离长度就可以了。
2.代数与平面转化
代数和平面几何的相互转化主要体现在有圆锥曲线的题型之中,这样的化归思想方法可以将问题简单化。比如有这样一道题:F1(-2,0),F2(2,0)是两个顶点,N为x2+y2=1这个圆形O上的任意一个点,现在M点和F1(-2,0)关于点N对称,F2M和F1M这条线段的中垂线相交于P,点P的轨迹是什么。有四个选项ABCD,分别对应为双曲线、椭圆、抛物线和圆。
通过题目所给条件,我们可以进行一定的转化得出图3。
然后连接O和N这两点,因为这两点是F1F2和F1M的中点,所以通过计算能够得出F2M=2,所以PM-PF2=2,PF1=PM,PF1-PF2=2。因此,可以算的这道题的答案是A,双曲线。
两者都是化归思想在几何当中的应用,除此之外还有着定点定值的转化、位置关系的转化和动点和定点之间的转化等。
结论:综上所述,化归思想在高中数学的学习当中十分广泛,想要学好高中数学,就必须具有良好的化归思想,然而,化归思想的强化与化归能力的提升并不是一朝一夕的事,还需要老师的教导以及学生的自我锻炼。
参考文献:
[1]杨社锋.化归思想在高中数学解题中的应用[D].河南大学,2014.
[2]李昀晟.化归思想在高中数学解题过程中的应用分析[J].数学理论与应用,2015,04:124-128.
[3]王志惠.化归思想在高中数学教学中的应用研究[D].内蒙古师范大学,2015.
(作者单位: 长沙麓山国际实验学校G1509班 410006)endprint
