基于POT模型的鸡蛋价格风险的VaR与ES度量

刘伟++朱新颜++张爱华++孙兆明

摘要：近年来我国鸡蛋市场所呈现出的大幅振荡走势给相关利益主体带来了巨大的价格风险，因此，对鸡蛋价格风险的精确度量有着重要的现实意义。通过对全国鸡蛋平均批发价格的实证研究表明，基于广义帕累托分布的极值理论的POT模型能够较好地拟合鸡蛋价格极端收益率数据，用POT模型来度量鸡蛋价格的风险价值是适合的。经过测算，在十年一遇、二十年一遇、百年一遇的情形下，衡量我国鸡蛋价格风险的VaR分别为0.81%、1.14%、2.15%，而在VaR超过上述百分比的条件下，鸡蛋价格的ES分别为1.38%、1.81%、3.10%。

关键词：鸡蛋价格；风险度量；POT模型；VaR；ES；帕累托分布；极端收益率

中图分类号： F323.7文献标志码： A文章编号：1002-1302（2017）08-0330-03

我国作为鸡蛋产销第一大国，鸡蛋价格的涨跌触动无数蛋鸡养殖户、鸡蛋贸易商以及消费者的神经。尤其是最近几年来，鸡蛋价格呈现出明显的大幅振荡的走势，如在2014年3月开始的6个月内，鸡蛋价格上涨了44%，并创下历史最高点，而在之后的8个月内，价格又下跌超过30%，给相关利益主体带来巨大的价格风险。因此，如何对在我国有着巨大市场的鸡蛋价格风险进行精确度量，便是一个具有重要意义的研究课题。然而，目前关于鸡蛋市场价格风险研究的相关文献还不多见。研究者更多从鸡蛋价格波动、预测以及预警的角度对鸡蛋价格展开研究。赵一夫等采用Census X12季节调整法和HP滤波法对鸡蛋价格波动展开研究，总结了我国鸡蛋价格长期的变动趋势和周期性波动规律，并分析了影响鸡蛋价格变动的因素[1]。谭银清等针对鸡蛋价格波动所呈现出的季节性、周期性、趋势性特点，通过构建向量自回归模型（VAR），分析鸡蛋价格与各影响因素之间的作用机制，以找出鸡蛋价格波动的成因[2]。徐明凡等利用灰色模型对鸡蛋价格进行相关分析及预测，并得出相对神经网络模型而言，灰色理论模型在对我国鸡蛋价格的预测上具有更有效的预测效果[3]。唐江桥等将自回归移动平均模型（ARMA）作为鸡蛋价格预测模型，运用黑色预警方法对鸡蛋价格的波动进行预警[4]。董晓霞等通过采用门槛自回归模型（TAR）、动量门槛自回归模型（M-TAR）和非对称误差修正模型（ATP-ECM），对鸡蛋的收购价格与零售价格之间是否存在非对称性传导效应进行了检验[5]。但也有少数学者从价格风险的角度对畜产品市场价格风险度量作出尝试。安丽等运用极值理论对我国生猪市场价格进行了拟合，采用VaR（value at risk，VaR）方法度量了我国生猪市场价格风险，并进一步计算了我国生猪市场价格十年一遇、二十年一遇、五十年一遇、百年一遇情况下的风险损失[6]。这为本试验鸡蛋价格风险问题提供了研究思路。张峭等提出利用VaR度量农产品现货市场风险，并计算了7种分布模型（Beta分布、Burr分布、正态分布、Log-Logistic分布、对数正态分布、Gamma分布和Logistic分布）下包括鸡蛋在内的5种畜产品的市场风险值VaR。根据对不同概率分布模型的拟合优度检验结果，认为我国畜产品的市场风险并不服从正态分布，运用VaR方法度量农产品市场风险是可行的[7]。虽然上述研究对鸡蛋价格风险的度量方面提供了有益的思路并作出了有价值的尝试，但有2点不足也不容忽视：首先，先验假设畜产品市场价格波动服从既定概率分布难以得到经验数据的支持。其次，在对价格风险的度量方面，VaR虽然是被广泛认同的最为常用和重要的风险度量方法，然而，由于这一度量方法的内在缺陷，如不满足次可加性等，因而并不是一致性风险度量。而预期不足（expected shortfall，ES）则具备更加优良的性质，是一致性的风险度量。基于上述考虑，本试验尝试引入极值理论研究鸡蛋价格风险度量问题，由于其无须对市场价格波动的整体分布作出假设，只须考虑价格波动的“尾部”，从而避免先验假定价格波动整体分布的缺陷。同时，在计算传统VaR的基础上，本研究也计算了ES，以实现对鸡蛋市场价格风险更为准确的度量。

1理论基础

极值理论（extreme value theory，EVT）是专门研究次序统计量极端值分布特征的理论，由于其仅考虑分布的尾部，因而能够比传统的正态分布更准确地描述分布的尾部特征，进而可以对风险价值进行更精确的度量。

1.1极值理论中的POT模型

極值理论是对损失分布的尾部进行建模，按照确立极值方法的不同，可分为2种模型：一是区域最大值（block maxima method，BMM）模型，利用广义极值分布对尾部进行拟合；二是超越门槛值（peaks over threshold，POT）模型，利用广义帕累托分布对尾部进行拟合。相比而言，POT模型由于能够更加有效地利用现有数据，从而在实践中被广泛采用。

2实证分析

2.1数据来源及描述性统计

本试验以我国鸡蛋批发价格日度数据为研究对象，选取2010年12月23日该数据发布以来至2015年4月21日之间共1 068个日收益率作为样本数据进行建模，计算VaR与ES。数据来自同花顺iFinD，用R软件进行数据处理。其中，日收益率计算公式为Rt（lnPt-lnPt-1）×100，Pt、Pt-1分别为第t、第t-1天的鸡蛋全国平均批发价格，并对Rt进行取负号处理。由于本研究采用的是日度数据，因此不需要对鸡蛋价格进行季节调整，同时也未对其进行通货膨胀平减处理，以反映鸡蛋利益相关主体所承担的实际价格波动风险。

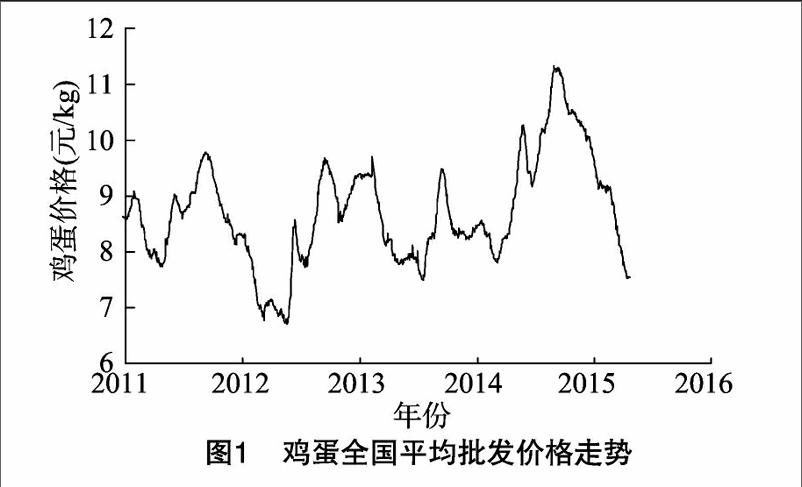
由图1可知，近年来我国鸡蛋价格呈现出大幅振荡的走势。2011年受河北省、内蒙自治区、东北等部分地区相继暴发禽流感的影响，鸡蛋价格一度出现大幅上涨。这激发了养鸡户的积极性，大量补栏，使得蛋鸡存栏量、产蛋量增加，导致鸡蛋价格又一路走低。而随着鸡蛋行情持续走低，许多养殖户开始淘汰蛋鸡，造成存栏量减少，鸡蛋在2012年又出现一轮上涨。进入2014年，受2013年鸡蛋行情持续低迷的影响，养殖户淘汰鸡开始增加，且没有进行有效的补栏，使得蛋鸡供应出现缺口，促使鸡蛋价格再次回升，并创出历史新高。而随着鸡蛋价格的一路走高，蛋鸡养殖利润提升，养殖户开始批量补栏。从2014年11月开始，后备鸡存栏量便开始一路增加。这为之后鸡蛋价格的大幅下跌埋下伏笔。因此，鸡蛋价格如坐过山车般上下波动，给蛋鸡养殖户、鸡蛋贸易商和消费者带来了巨大的价格风险。

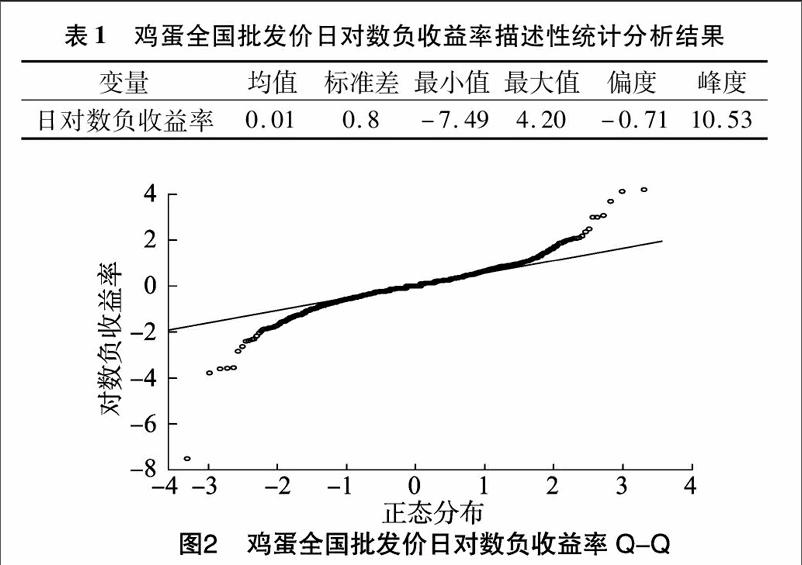
样本描述性统计量见表1。样本的JB统计量为 5 048.448，p值为0，从而拒绝正态分布的初始假设。样本数据Q-Q见图2。

由于样本峰度远大于3，且图2有上凸下凹的特点，判断样本具有厚尾性。因此，适合应用极值理论对鸡蛋市场价格风险进行测度。本研究运用GPD对样本分布尾部进行拟合，并采用最常用的MLE法对模型参数进行估计。

2.2阈值的确定及GPD参数的估计

本研究应用平均超限函数（mean excess function，MEF）图法确定阈值。MEF图见图3，在0.9处，MEF图随阈值的变化呈直线状，所以选取阈值μ=0.9。在此阈值条件下，超限样本数为88，占总样本的8.23%。

运用MLE法对模型参数进行估计，其中尺度参数 0.462 3、尺度参数标准差0.085 5、形状参数0.223 6、形状参数标准差0.153 0。

安丽等研究发现，我国生猪市场收益率风险概率分布的形状参数为负值，表明拟合生猪市场极端收益率数据的GPD是截尾的，即有有限个右端点[6]。但在本试验对鸡蛋市场极端收益率数据的拟合中，得出的GPD的形状参数为正值，表明鸡蛋市场价格的分布是厚尾的，且无上界。这一结果更符合鸡蛋市场价格的实际波动状况。

2.3样本拟合效果及参数稳定性的检验

对模型拟合效果进行诊断，结果见图4。由图4可知，P-P图上的点基本处于对角线上，Q-Q图中右上方的点离对角线有少许偏离，但从重现水平图可以看出其仍然处于置信水平之内。因此总得来说，样本拟合效果可以接受（图5）。

为验证所估计参数的稳定性，对不同阈值下参数的变化进行绘图，结果见图6。由图6可知，选定的阈值附近参数估计值未呈现离散状况，显示模型参数具有一定的稳定性，也表明阈值的选取是合适的。

2.4VaR与ES风险价值的计算

将估计结果代入公式（7）、公式（10），即可求得不同置信水平下的VaR、ES，结果见表2。

3小结

本试验运用极值理论的POT模型研究我国鸡蛋市场的价

格波动问题，不仅采用标准的VaR方法，还采用具有一致性风险测度的ES法对鸡蛋价格波动风险进行度量。主要得出以下2点结论：（1）通过对全国鸡蛋批发价格日对数收益率的实证研究发现，广义帕累托分布能够较好地拟合鸡蛋批发价格极端日收益率的数据，表明运用极值理论的POT模型度量鸡蛋批发价格的风险价值是适合的。（2）由于价格的对数收益率近似于价格变动的百分比，因此基于对数收益率所计算得到的VaR与ES也可以被视为价格变动的比例。从本试验对全国鸡蛋批发价格风险价值的测度结果得出，在不同置信水平下，即十年一遇（0.90）、二十年一遇（0.95）、百年一遇（0.99）情形下，日损失率分别为0.81%、1.14%、2.15%，同时，在日损失率超过上述百分比的条件下，平均损失率分别为1.38%、1.81%、3.10%。

參考文献：

[1]赵一夫，秦富. 我国鸡蛋价格变动特点及规律分析[J]. 农业技术经济，2013（1）：4-10.

[2]谭银清，王钊，陈益芳. 我国鸡蛋价格波动的特点及影响因素分析[J]. 畜牧与兽医，2015，47（1）：125-129.

[3]徐明凡，刘合光. 关于我国鸡蛋价格的预测及分析[J]. 统计与决策，2014（6）：104-107.

[4]唐江桥，雷娜. 中国鸡蛋价格波动预警研究[J]. 西部论坛，2011，21（6）：44-49.

[5]董晓霞，胡冰川，于海鹏. 我国鸡蛋市场价格非对称性传导效应研究——基于非对称误差修正模型[J]. 农业技术经济，2014（9）：52-60.

[6]安丽，郭军. 基于极值理论的生猪市场价格风险评估研究[J]. 农业技术经济，2014（3）：33-39.

[7]张峭，王川，王克. 我国畜产品市场价格风险度量与分析[J]. 经济问题，2010（3）：90-94.

[8]Lii J P. Statistical inference using extreme order statistics[J]. Annals of Statistics，1975，3（1）：119-131.