基于弯矩图面积法求解梁的弯曲问题

张洛明，何春霞，张发厅

（黄河科技学院 机械工程学院，河南 郑州 450063）

·实验技术·

基于弯矩图面积法求解梁的弯曲问题

张洛明，何春霞，张发厅

（黄河科技学院 机械工程学院，河南 郑州 450063）

为了简化梁的平面弯曲变形计算，该文通过对梁的挠曲线近似微分方程的建模分析，推导出用弯矩图面积法求解梁的变形问题的计算公式。当梁的抗弯刚度为常量，且弯矩图面积及弯矩图形心容易得到时，利用梁上支座处的已知边界条件，无需积分即可求解梁上任意横截面的转角和挠度；与叠加法相比，也有概念清晰、计算快捷的优点。实践表明，即使在梁上作用有分布载荷使得弯矩图面积及形心不容易直接得到的情况下，稍加推广即可方便求解梁的变形问题。

面积；弯矩；形心；转角；挠度

梁的弯曲问题是材料力学教学中的重点内容，在实际设计及工程实践中也有很强的应用价值，是机械类学生与工程技术人员必须掌握的知识。在国内现行的教材体系中，均是采用积分法和叠加法来处理弯曲问题的。然而，这些方法比较繁琐，运用时容易出错，成了很多学生学习上的难点。本文从基本的挠曲线近似微分方程出发，结合直观的弯矩图，给出了一种“弯矩图面积法”，易于掌握，可用来求解梁的弯曲问题。

1 积分法与叠加法的基本原理

在现行的教科书［1－3］中，对于如图1所示的右手直角坐标系统，梁变形后的转角θ（逆时针为正）和挠度y（向上为正）分别可表示为［4－5］：

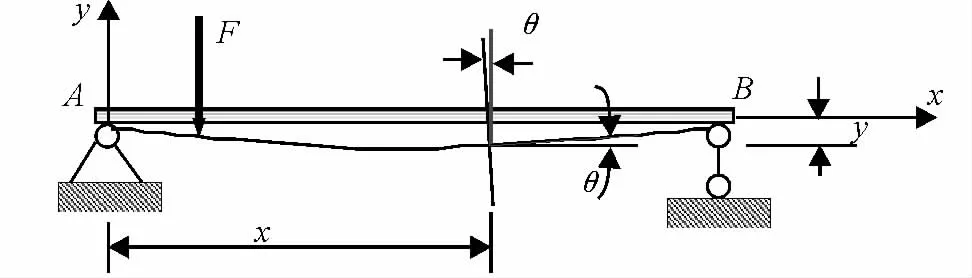
图1 右手直角坐标系下的挠曲线转角及挠度

式中，C、D为积分常数。

式（1）和式（2）就是求解梁的弯曲变形情况的基础公式，可以通过积分运算及考虑边界条件得到转角和挠度的沿梁轴线变化的函数表达式θ＝f1（x）和y＝f2（x），据此可以计算出梁上任意横截面的挠度和转角，这种方法是积分法。

对于只需知晓梁的某些特殊横截面的变形情况时，一般教科书和设计手册上都会给出梁在简单载荷作用下的变形表［6－7］以供使用叠加法求解时使用。

积分法的运算过程比较繁琐，尽管在梁上作用有多个载荷时可以利用所谓阶梯函数［8－9］来简化计算，但仍需要根据边界条件计算出积分常数；叠加法在载荷比较复杂时需要仔细分析将其代换为表中所列出的基本载荷形式后再行叠加，稍有不慎就易出错。

2 弯矩图面积法的推导

对于抗弯刚度EI为常量，且弯矩图相对简单的情况，可以用弯矩图面积法［10－11］来求解梁的任意横截面的变形问题，简便而实用。

如图2所示，曲线AB为梁的挠曲线的一部分，A、B两个横截面的转角和挠度分别为θA、yA和θB、yB。则对挠曲线的近似微分方程为：

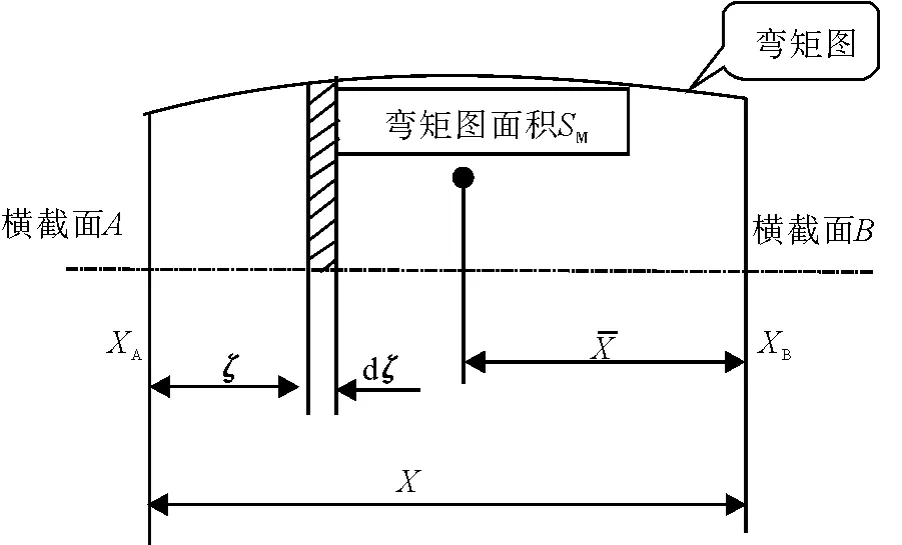
图2 弯矩图面积法示意图

进行一次在区间［xA，xB］上的定积分，即可得到：

即横截面B的转角θB大小等于横截面A的转角θA的值与两横截面之间的弯矩面积除以EI的值之和。

同理，再次积分，就有：

即横截面B的挠度yB大小等于横截面A的挠度yA的值、横截面A的转角θA和两横截面之间距离乘积的值以及两横截面之间的弯矩图面积SM与该面积的形心到横截面B的距离的乘积S除以EI的值这三者之和。

由于以上推导过程中的A、B两个横截面可以根据实际情况灵活确定，所以理论上利用上述式（6）和式（11），就可以求得梁上任意横截面的转角和挠度。使用中要注意，一是弯矩图若在粱的轴线下方，则相应的面积为负值。二是横截面B也完全可以在横截面A的左边，此时的x仍然是弯矩图面积形心到横截面B的值。

3 应用举例

为了便于比较，在此以两个一般教科书上常见的题目为例，展示一下弯矩图面积法的解题步骤。

例1 讨论如图3所示简支梁的弯曲变形。设EI为常量。

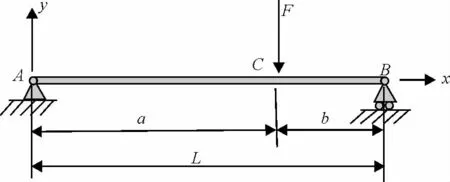
图3 简支梁

解：先求出支座反力后，粱的弯矩图很容易画出如图4所示。

图4 简支梁弯矩图

利用式（11）得出：

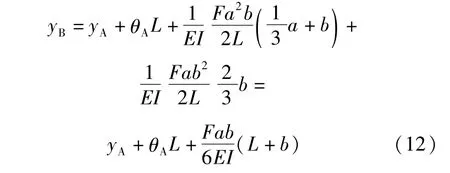
因为A、B为铰链支座，yB＝yA＝0，所以可得：

负号表示挠度向下。

如果需要的话，此方法也可以方便地求出挠曲线的转角方程和挠度方程：

例2 试求图5所示外伸梁截面B的转角和端点C的挠度。设EI为常量。

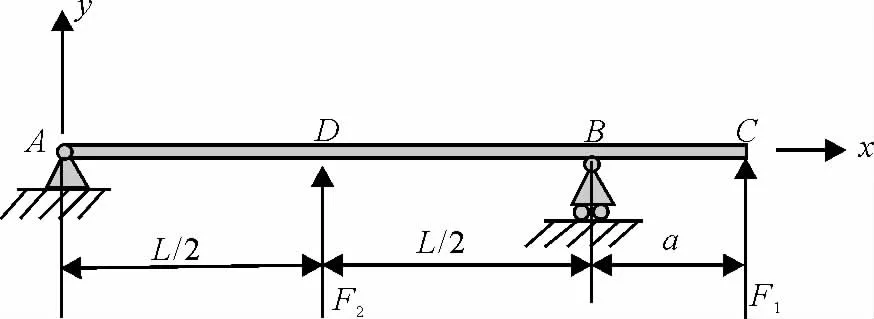
图5 外伸梁

解：先分别求出F1、F2单独作用下的弯矩图，如图6、图7所示。

图6 F1单独作用下的弯矩图

图7 F2单独作用下的弯矩图

注意到图7的弯矩图面积为负面积：

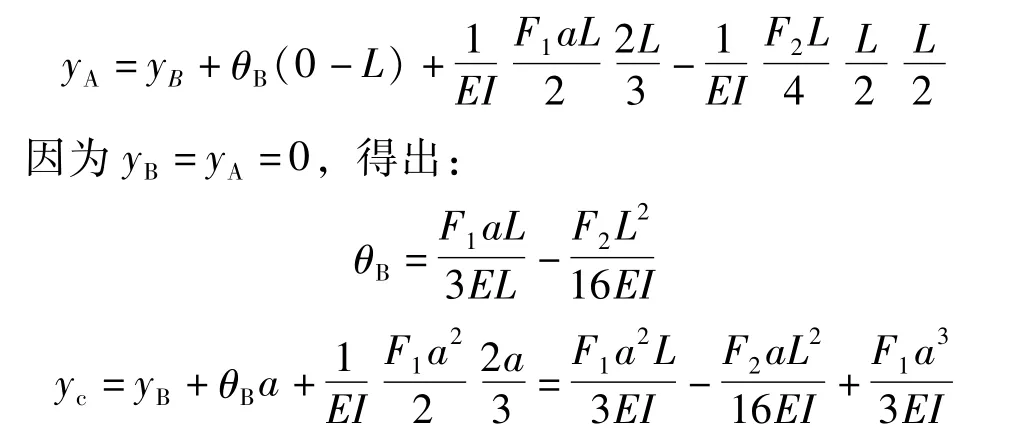
可见，比用常规的叠加法更简明。

4 结束语

综上所述，当弯矩图面积及形心容易得到时，相比于积分法和叠加法，用弯矩图面积法求解梁的变形问题时，具有概念清楚、计算简明、使用方便的特点。事实上，即使对于梁上作用有分布载荷使得弯矩图面积及形心不容易直接得到的情况，也同样可以将式（6）中的和式（11）中的分别用和）dζ来计算即可。

［1］刘鸿文.材料力学［M］.4版.北京：高等教育出版社，2004.

［2］刘鸿文.材料力学I［M］.5版.北京：高等教育出版社，2012.

［3］孙训方.材料力学II［M］.6版.北京：高等教育出版社，2009.

［4］章宝华.材料力学［M］.北京：北京大学出版社，2014.

［5］奚绍中，邱秉权.工程力学教程［M］.3版.北京：高等教育出版社，2016.

［6］杨伯源.材料力学I［M］.北京：机械工业出版社，2006.

［7］成大先.机械设计手册［M］.4版.北京：化学工业出版社，2015.

［8］何春霞，吴雁平.用单位阶梯函数求解变载荷梁挠度的方法［J］.实验科学与技术，2014，12（4）：13－14.

［9］汤志浩.单位阶梯函数的性质及其应用［J］.湖南工程学院学报（自然科学版），2009，19（4）：78－79.

［10］李银山，官云龙，桑建兵.Maple在材料力学中的应用（六）——连续分段独立一体化积分法［C］／／第十五届北方七省、市、区力学学术会议论文集.山西：山东省力学学会，2014.

［11］GERE JM，GOODNO B J.Strength of Materials［M］.北京：机械工业出版社，2015.

［12］同济大学数学系.高等数学［M］.7版.北京：高等教育出版社，2014.

Solving the Bending Problem of Beam Based on Bending M oment Diagram Area M ethod

ZHANG Luoming，HE Chunxia，ZHANG Fating
（Department of Mechanical Engineering，Huanghe S＆T College，ZhenZhou 450063，China）

In order to simplify the calculation of the plane bending deformation of the beam，this paper deduces the calculation formula of the deformation of the beam by themethod of themoment diagram area.When the beam bending stiffness is constant，and themoment diagram and bendingmomentgraph easier to obtain，the corner and the deflection of any cross section of the beam can be solved without using the integral boundary condition at the bearing on the beam.Compared with the superposition method，there are al so clear concept，the advantages of quick calculation.Practice shows that even if the distribution of the load on the beam makes the bendingmoment area and the centroid is noteasy to be obtained directly.，A little promotion can easily solve the problem of the beam deformation.

area；moment；poid；angle；deflection

O341；G642.423

A

10.3969／j．issn．1672－4550.2017.03.007

2015－11－13；修改日期：2017－04－18

河南省民办高校品牌专业“机械设计制造及其自动化”（ZLG201601）。

张洛明（1955－），男，博士，教授，主要从事连续体力学的研究和设计工作。