基于RPCA的纸病图像分割算法

亢 洁 潘思璐 王晓东

(陕西科技大学电气与信息工程学院,陕西西安,710021)



基于RPCA的纸病图像分割算法

亢 洁 潘思璐*王晓东

(陕西科技大学电气与信息工程学院,陕西西安,710021)

针对实际纸病检测应用中采集到的图像分辨率越来越高,在图像处理过程中出现数据维数过大的问题,提出一种基于鲁棒主成分分析法(Robust Principal Component Analysis,RPCA)的纸病图像分割算法,该算法将纸病图像对应的矩阵分解成稀疏矩阵和低秩矩阵。在后续检测中只需选取稀疏矩阵对应的图像进行检测就可以满足纸病检测的要求,有效减少了计算量,最终节省了整个纸病检测环节的检测时间。仿真结果表明,该方法可用于纸病图像的分割,并且具有良好的分割效果。

数据冗余；RPCA；图像分割；纸病检测

在经济日益发展的今天,造纸行业的竞争越来越激烈,提高纸产品的质量成为各造纸厂家提高市场竞争力的有效途径。然而在实际的生产过程中,会因多种原因使得最终生产出的纸张含有缺陷,最为常见的纸病有褶皱、裂纹、黑斑和亮斑等[1-2]。因此，对生产出的纸张进行缺陷检测显得尤为重要。在纸病检测过程中需对采集到的纸张图像进行分割。现有的图像分割方法主要有4类：基于阈值的分割方法[3]、基于形态学的分割方法[4]、基于统计学的分割方法和基于小波的分割方法[5]。基于阈值的分割方法原理简单,但对于不同的纸病需要选取不同的阈值。基于形态学的分割方法具有较好的抗干扰性,但形态学运算的结果在很大程度上依赖着其结构元素的选取,而结构元素的选取并没有有效的准则,只能依靠多次实验或经验。基于统计学的分割方法容易实现,但鲁棒性有待于提高,对周围环境(如光照强度)的变化适应性差。基于小波的分割方法精度较高,但精度的提高是以减慢运算速度为代价的。

在实际的纸病检测应用中,随着用于采集纸病图像的器件精度的提高,图像分辨率越来越高,使得采集到的图像数据量越来越大。在检测处理时,数据量太大,会增大计算量、影响纸病检测的效率,最终降低纸病检测的实时性[6]。

针对以上问题,本研究提出一种基于鲁棒主成分分析法(Robust Principal Component Analysis,RPCA)的纸病图像分割算法。该算法通过RPCA将纸病图像对应的矩阵进行分解,将原纸病图像有效地分解成低秩矩阵图像和稀疏矩阵图像。其中,低秩矩阵图像表现为背景图像,稀疏矩阵图像表现为缺陷图像。这样,很容易地将背景图像和缺陷图像分离。后续再对稀疏矩阵图像进行检测,从而识别出有无纸病缺陷的存在。这样可将检测中不需要的背景图像中的信息去除,从而达到去除冗余数据的目的。

1 主成分分析法

主成分分析法(Principal Component Analysis,PCA)[7]是最常用的数据降维方法。该方法的实质是在尽可能好地代表原始数据的前提下,通过线性变换将高维空间中的样本数据投影到低维空间中,从而达到既保证原有特征的主要信息,又降低数据维数的目的。即,对于给定数据向量x,PCA能从中分解出原始低秩数据向量y和干扰项e,即x、y和e满足式(1)的关系：

x=y+e

(1)

在统计学上,该分解问题可归结为探索数据主成分的问题,当干扰项e遵循小方差的高斯分布时,PCA能够通过对给定数据向量x使用退化的高斯分布建模[8]或者奇异值分解等方法解决探索数据主成分的问题。

例如：对于数据向量x=[x1,x2,…,xn],其中,xi从式(1)中产生,PCA能够通过最小化式(1)得到数据向量x的低秩投影重建：

(2)

其中,Ir是一个大小为r×r的单位矩阵,‖x-UUTx‖F是矩阵的F范数。

根据式(2)并通过奇异值分解的方法,可以估算出数据向量x的主成分y：

y=U*(U*)Tx

(3)

其中,U*是通过求解式(2)得到的,即计算数据向量x的奇异值。

PCA具有计算稳定及计算效率高的优点,其已被广泛应用到计算机视觉领域的许多方面,如数据表示、模式识别、降维和图像信息简化和压缩等。

然而在实际应用中,PCA的应用和性能会因为缺乏鲁棒性而受到限制。例如,当干扰项e为小噪声且呈独立高斯分布时,PCA可以通过奇异值分解准确地找到最优的低秩项y,但是,当干扰项e被严重破坏,即干扰项e很大时,PCA对低秩项y的估计不准确,且PCA需要在计算之前预知子空间的维数。

2 RPCA

针对PCA的缺陷,近年来提出了一种RPCA方法。RPCA的核心思想是将受到干扰的矩阵分解成低秩矩阵和稀疏矩阵,可用式(4)表示,即：

x=y+e

(4)

其中,x表示高维图像矩阵,y表示低秩矩阵,e表示代表干扰项的稀疏矩阵。同时,式(4)也可转化为优化式(5)所示的目标函数的优化问题,对于一个给定的数据向量x,RPCA可以通过求解式(5)求得其主成分y。

(5)

其中,x为给定的数据向量,即图像处理中输入的图像矩阵x∈NH·W(H和W为矩阵的维度,即图像的高度和宽度)；y是低秩的背景矩阵；e是稀疏矩阵,即干扰项,相对于整个图像来说,稀疏矩阵只含有少量的非零或非1点。‖e‖0是矩阵的0阶范数,表示矩阵中的非零元个数。对式(5)进行优化是一个非确定性多项式(NP)难问题,通常没有有效的求解算法,所以式(5)一般被转化为式(6)所示的凸优化问题。通过优化式(6)所示的目标函数,可将数据向量x分解。

(6)

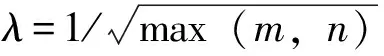
由上述可知,RPCA与PCA两者之间的相同体现在其本质上均为寻找高维数据在低维空间上的最佳投影,即找到高维数据的主成分,起到去除冗余数据的作用；两者的不同点在于,PCA假设数据中的干扰项是呈高斯分布的,大的干扰点或严重的离群点会影响PCA,从而使其无法正常工作,而RPCA不存在这个假设,RPCA只是假设其干扰项是稀疏的,而不管干扰项以什么方式稀疏。

3 基于RPCA的纸病图像分割算法

RPCA主要应用在人脸识别[11]、医学图像[12]、物体识别[13]、网络流量异常检测[14]等领域。在图像处理领域，RPCA的优势是：其可将图像的矩阵分解成2个部分,即低秩矩阵与稀疏矩阵,然后再根据相应的应用需要对分解后的稀疏矩阵对应的图像进行处理,而对于低秩矩阵对应的背景图像中对检测无用信息就可舍去。如在对纸病进行分类时,可提取稀疏矩阵对应图像的特征并用作分类的特征；或者在对纸病图像进行边缘检测时,可直接对稀疏矩阵所对应的图像进行边缘检测即可。将RPCA应用于图像处理过程中可有效地加快整个图像处理环节的处理速度。

本研究首次将RPCA应用到纸病图像的分割过程中,这是因为除了可能存在的缺陷外,待测纸张大部分的内容都是线性相关或相似的,它们满足低秩的性质,而可能存在的缺陷则可以被认为是稀疏矩阵里的元素。鉴于此发现,本研究提出了基于RPCA的纸病图像分割算法。

传统的纸张缺陷预处理分割算法要采用图像滤波、灰度统计、阈值分割、边缘检测等方法来完成纸张缺陷的分割。不同于传统的纸张缺陷分割方法,基于RPCA的纸病分割算法将图像的分割问题转化为RPCA的矩阵分解问题,即利用RPCA将输入的纸病图像矩阵分解为低秩矩阵和稀疏矩阵,其中,低秩矩阵可表现为原纸病图像的背景图像,而稀疏矩阵则可表现为原纸病图像的缺陷图像。这样很容易地将背景图像和缺陷图像分割出来,然后选取含有纸张缺陷的稀疏矩阵图像作为目标图像,通过检测含有纸张缺陷的目标图像就可识别出有无纸张缺陷的存在,从而达到去除冗余数据的目的。

图1 基于RPCA的黑斑纸病图像的分割结果

图2 基于RPCA的孔洞纸病图像的分割结果

图3 基于RPCA的亮斑纸病图像的分割结果

本研究采用以下步骤进行纸病图像的分割,具体分割步骤如下。

步骤1：对读入的纸病图像进行灰度化处理。

步骤2：利用RPCA,将纸病图像矩阵分解为低秩矩阵和稀疏矩阵,低秩矩阵对应背景图像,稀疏矩阵对应有缺陷的图像(即检测中所需的目标图像)。

步骤3：将分解后得到的稀疏矩阵所对应的图像进行二值化处理,得到基于RPCA的纸病分割的最终分割结果。

为验证基于RPCA的纸病图像分割算法的有效性,本研究分别选择含有黑斑、孔洞、亮斑以及裂纹4种常见纸病的纸张图像作为实验对象,在Matlab R2010b,计算机配置为windowsXP、CPU为2.89 GHz、内存为1.91 GB的实验平台上进行仿真实验,仿真结果如图1～图4所示。

仿真结果表明,基于RPCA的纸病图像分割算法能够有效分割纸病图像。图1～图4中的最终分割结果表明,利用RPCA对纸病图像进行分割可起到一定的图像滤波作用,所有的最终检测结果几乎没有噪声；分割得到的纸张缺陷清晰、形状完整。

通常，传统的缺陷检测方法需对待检测图像先进行图像滤波、图像增强等预处理,然后采用阈值分割或者边缘检测等方法完成分割任务,最后再提取纸病图像中的纸病特征等后续处理。张学兰等[15]提出的双阈值分割算法的纸病检测部分就是按上述流程对纸病图像进行缺陷检测,首先计算纸病图像的背景灰度均值,并将图像背景灰度均值的1.15倍和0.70倍作为阈值对纸病图像进行分割,然后对分割结果分别运用Prewitt算子和形态学闭合运算,最后再将闭合运算结果与双阈值分割结果使用图像合成加运算,得到最终结果。同样以上述4张纸病图像为实验对象,在Matlab中对双阈值分割算法进行仿真,得到如图5所示的分割结果。

图4 基于RPCA的裂纹纸病图像的分割结果

图5 双阈值分割算法的最终检测结果

图6 双阈值分割算法检测结果的二值化结果

为了便于将双阈值分割算法的结果与基于RPCA的纸病图像分割算法的结果进行对比,将双阈值分割算法的最终检测结果进行二值化处理,结果如图6所示。

本研究分别采用基于RPCA的纸病分割算法和双阈值分割算法进行纸张缺陷检测,并将检测结果进行对比,得到如下结论。

(1)采用基于RPCA的纸病图像分割算法与双阈值分割算法分别对4种常见纸病进行分割的运算时间如表1所示。从表1可以看出,两者的运行时间相差不大。

(2)对比2种分割算法的仿真结果可知,双阈值分割算法的分割效果比基于RPCA的纸病图像分割算法差,其将原纸病图像中缺陷的形状改变了一些、甚至出现了丢失,这在对裂纹纸病图像和孔洞纸病图像的分割结果中表现得尤为明显。基于RPCA的纸病图像分割算法分割得到的缺陷的外边缘和整体形状更完整,更接近于原纸病图像中的原图像,减小了原纸病图像中缺陷形状与分割结果的缺陷形状之间的误差,从而更加有利于后续的纸病分类识别等操作。

(3)双阈值分割算法等传统缺陷分割方法需要大量的图像预处理过程,如滤波等操作,流程繁琐复杂。而基于RPCA的纸病图像分割算法只需要将RGB图像转化为灰度图像,具有操作简单的优点；该方法虽未经过滤波,但仍具有一定的抗噪性。计算基于RPCA的纸病图像分割算法的结果与双阈值分割算法的二值化结果的峰值信噪比(PSNR)和均方误差(MSE),结果见表2。

表2 基于RPCA的纸病图像分割算法与双阈值分割算法的MSE和PSNR

从表2可以看出,双阈值分割算法只有对黑斑纸病的PSNR略高于基于RPCA的纸病图像分割算法。综合这几种纸病的数据可知,基于RPCA的纸病图像分割算法的抗噪性略好于双阈值分割算法。

(4)基于RPCA的纸病图像分割算法可减少数据处理过程中一些不重要的数据,有利于简化后面的运算,可减少整个纸病检测或识别过程的运算时间。

4 结束语

鲁棒主成分分析法(RPCA)的问题是一个低秩矩阵与稀疏矩阵分解的问题,在分解过程中,其将原来的非确定性多项式(NP)难问题转化为凸优化问题,然后通过求低秩矩阵的核范数和稀疏矩阵的1阶范数来简化问题,最终得到最优解。本研究提出一种基于RPCA的纸病图像分割算法,该分割算法充分利用了RPCA能够去除冗余数据的特性。仿真结果表明,基于RPCA的纸病图像分割算法能够将纸张图像中含有的缺陷有效地分割出来,并且具有较好的分割效果。

在基于RPCA的纸病图像分割算法的凸优化问题的求解方面,如何有效并快速地求解是一个值得探索的问题；此外,如何在现场可编程门阵列(FPGA)等硬件平台上实现该算法,并将其应用到纸病的在线检测中,将是今后研究中亟需解决的问题。

[1] Shi H Q, Guo K Y, Sun Y N, et al. Extraction of Hemicellulose from Acacia Wood via Autohydrolysis and Ethanol Precipitation[J]. Paper and Biomaterials, 2016, 1(1): 1.

[2] Dong R X, Mei X W, Ma C, et al. Structural Changes of Wheat Straw Lignin during Formic Acid Treatment[J]. Paper and Biomate-rials, 2016, 1(2): 16.

[3] 殷燕屏, 熊智新, 胡慕伊. 基于阈值分割及分形特征的纸病图像识别算法研究[J]. 中国造纸学报, 2011, 26(4)： 41.

[4] 陈 珺, 王亦红. 基于机器视觉的低对比度纸病识别算法研究[J]. 中国造纸学报, 2013, 28(2)： 29.

[5] 周 强, 张 慧, 杨雁南. 基于两次二维Daubechies小波变换的纸病在线辨识方法研究[J]. 中国造纸学报, 2014, 29(3)： 47.

[6] 杨 波, 周 强, 张刚强. 基于几何及灰度特征的纸病检测算法研究[J]. 中国造纸, 2011, 30(9): 50.

[7] 邓洪波, 金连文. 一种基于局部Gabor滤波器组及PCA+LDA的人脸表情识别方法[J]. 中国图象图形学报, 2007(2): 322.

[8] Ma Y, Derksen H, Hong W,et al. Segmentation of multivariate mixed data via lossy data coding and compression[J]. IEEE Trans Pattern Anal Mach Intell, 2007, 29(9)： 1546.

[9] Fang L, Li S, Nie Q, et al. Sparsity based denoising of spectral domain optical coherence tomography images[J]. Biomedical Optics Express, 2012, 3(5): 927.

[10] Candes E, Li X, Ma Y, et al. Robust principal component analysis[J]. Journal of the ACM, 2011, 58(3): 11.

[11] Liu W, Xie X, Lam K M. An efficient method for occluded face recognition[C]//International Conference on Pattern Recognition. Japan. 2012: 2993.

[12] Patel V M, Maleh R, Gilbert A C, et al. Gradient-Based Image Recovery Methods From Incomplete Fourier Measurements[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2012, 21(1): 94.

[13] Zhang Z, Ganesh A, Liang X, et al. TILT: Transform Invariant Low-Rank Textures[J]. International Journal of Computer Vision, 2012, 99(1): 1.

[14] Mardani M, Mateos G, Giannakis G B. Recovery of Low-Rank Plus Compressed Sparse Matrices With Application to Unveiling Traffic Anomalies[J]. IEEE Transactions on Information Theory, 2012, 59(8): 5186.

[15] 张学兰, 李 军, 孟范孔. 一种基于机器视觉的纸病识别方法[J]. 中国造纸学报, 2013, 28(1): 48.

(责任编辑：陈丽卿)

Segmentation Algorithm of Paper Defect Images Based on RPCA

KANG Jie PAN Si-lu*WANG Xiao-dong

(SchoolofElectricalandInformationEngineering,ShaanxiUniversityofScienceandTechnology,Xi’an,ShaanxiProvince, 710021) (*E-mail: pansilu098@163.com)

In the practical detection, the resolution of collected image is getting higher and higher, resulting the data dimension is too large in image processing, a paper image segmentation algorithm based on Robust Principal Component Analysis (RPCA) was proposed in this paper. The matrix of paper defect image could be decomposed into sparse matrix and low rank matrix. In the subsequent detection, just selecting the image corresponded by the sparse matrix for detection could meet the requirements of paper defect detection, and reduce the amount of computation effectively, and eventually reduce the detection time of the whole paper defect. The simulation results showed that the proposed algorithm could be used for the segmentation of the paper image and had good segmentation performance.

data redundancy; RPCA; image segmentation; paper defect detection

2016- 03- 29

陕西省自然科学基础研究计划项目(2014JM8329)；陕西省教育厅专项科研计划项目(14JK1092)；咸阳市科技计划项目(2011K07- 03)；陕西科技大学博士科研启动基金(BJ10-10)。

亢 洁,女,1973年生；博士，副教授；主要研究方向：缺陷检测、模式识别。

*通信联系人：潘思璐,E-mail:pansilu098@163.com。

TS736+.2

A

1000- 6842(2017)02- 0039- 06