CrMoWV钢的应力松弛行为及其预测

曹铁山，程从前，朱月梅，张弘伟，刘松峰，赵 杰

(1 大连理工大学 材料科学与工程学院，辽宁 大连 116085；2上海汽轮机有限公司，上海 200240)

CrMoWV钢的应力松弛行为及其预测

曹铁山1，程从前1，朱月梅2，张弘伟2，刘松峰2，赵 杰1

(1 大连理工大学 材料科学与工程学院，辽宁 大连 116085；2上海汽轮机有限公司，上海 200240)

以12Cr-1Mo-1W-0.25V耐热钢550，600℃的8760h松弛实验数据作为对象，研究短时间松弛数据准确而有效预测长时间松弛应力的方法。在采用松弛模型对长时间松弛应力进行直接拟合外推时，发现模型参数与所采用拟合数据的时间长度呈规律性的变化。提出考虑模型参数规律变化的时序参数法，以高精度预测长时间松弛应力。通过对比时序参数法与直接拟合外推法的预测结果，认为时序参数法在用短时间松弛数据预测长时间松弛应力上具有明显优势，预测结果的准确性较直接外推法高。

应力松弛；松弛模型；时序参数法；预测

应力松弛是各种材料在服役过程中普遍存在的一种应力衰退现象，是应力作用下材料内部弹性分量逐渐转化为塑性分量的结果[1,2]，同时也是某些合金高温失稳的重要因素[3]。应力松弛问题是工程上对紧固件进行机械设计时所关注的重点之一，通常的做法是先测量应力在较长时间松弛实验中的变化规律，然后根据规律性预测其在设计服役寿命时的松弛应力[4]。另外，在松弛行为的研究当中，松弛与蠕变之间的相互转化关系也引起关注[5-7]，其目的在于利用应力松弛实验在短时间内获得较多的蠕变数据以缩短高温蠕变强度设计所需时间。目前的研究表明，在松弛的第二阶段，两者有很好的相互转化关系[8,9]。但是，在温度相对较低的实验条件下(如模拟服役条件)，进入松弛第二阶段仍然需要很长的时间，同样需要长时间的松弛实验数据。

应力松弛实验是在总应变恒定不变的基础上，研究外部应力随实验时间变化规律的方法[10]。在进行松弛应力外推预测时，通常是根据已有的松弛应力-时间规律及松弛模型进行直接拟合外推得到设计寿命时的松弛应力。另外，由于松弛应力随着实验时间的非线性变化特点，一般认为，准确预测长时间松弛应力，必须开展较长时间的松弛实验。但是，目前普遍使用的这一方法面临两个方面的问题：(1)松弛实验耗费时间长，过程控制的精度要求高，松弛实验的难度增大；(2)即使实施了数千小时甚至更长时间的松弛实验，其长时间预测结果的精度仍然存在质疑，如预测模型的准确性，实验材料的可重复性等。总之，用长时间松弛实验来提高预测准确性是一种耗时费力且预测结果精度仍然存在质疑的方法。工程上在进行长时间松弛应力进行预测时，通常是采用比较成熟的模型进行直接拟合预测，但是，成熟模型[11]的普适性仍然存在疑问。而根据已有的松弛模型及现有的松弛应力预测技术，利用短时间的松弛实验数据准确预测长时间松弛应力，是学术界和工程界所关注的问题[12-14]。

本工作以12Cr-1Mo-1W-0.25V钢在550，600℃时的长时间应力松弛数据为研究对象，分析了在用短时数据预测长时数据时所采用数据的时间长度对模型直接拟合外推法预测结果的影响，研究了拟合方程参数与数据的时间长度之间的关系，在此基础上提出了基于短时数据的高精度预测长时间松弛应力的方法——时序参数法，并结合直接拟合外推法的预测结果和真实的实验数据验证了时序参数法预测结果的准确性。

1 实验材料与方法

1.1 应力松弛数据

图1为12Cr-1Mo-1W-0.25V耐热钢在550，600℃的长时间应力松弛曲线。实验时间为8760h，初始预应变为0.2%。可以看出，550℃的应力松弛速率相对较慢，实验结束时剩余应力仍然较高，为91MPa，而600℃时具有较快的松弛速率，实验结束时的剩余应力较低，仅为8MPa。

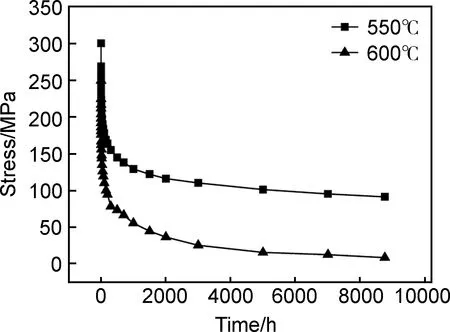
图1 12Cr-1Mo-1W-0.25V耐热钢的应力松弛曲线Fig.1 Stress relaxation curves of 12Cr-1Mo-1W-0.25V heat-resistant steel

1.2 松弛数据分析预测方法

在对12Cr-1Mo-1W-0.25V耐热钢松弛实验数据进行拟合分析时，选用公式(1)进行相关的探讨。

σ=σ0-aln(bt+1)

(1)

式中：σ为松弛应力；σ0为初始应力；t为实验时间；a，b为常数，一般通过直接拟合得到。

为研究数据的时间长度对松弛应力预测结果的影响，将550，600℃的长时间松弛数据进行分组，分组结果如表1所示。每组数据均以初始零时刻为起点以某时刻ti为终点：如数据组t50-Z表示0～50h时间段的松弛数据，其他组数据的处理依此类推。

对表1中各组数据分别进行分析处理：①用公式(1)进行拟合得到拟合方程，然后根据拟合方程直接外推出8760h的松弛应力，以分析拟合时所采用数据组的时间长度对外推结果的影响；②分析各拟合方程中参数a，b的变化规律，建立关系模型，然后对公式(1)所示的模型进行修订——时序参数法，并采用该方法进行预测；③将直接拟合外推结果与时序参数法的预测结果和实验数据进行比较，分析时序参数法预测结果的准确性；④将本工作提出的时序参数法应用于其他实验条件的松弛应力预测以分析该方法的适用性。

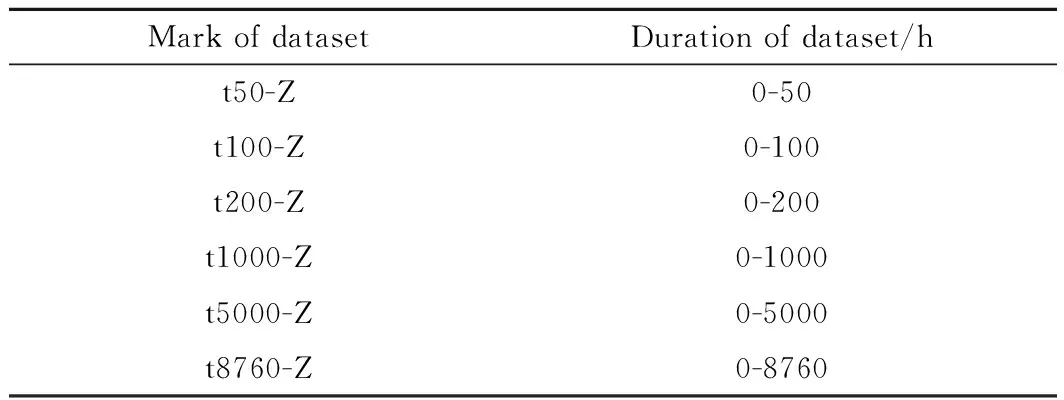
表1 松弛数据分组Table 1 Group of relaxation data

2 结果与分析

2.1 直接拟合外推的结果

图2是采用表1中的分组数据对12Cr-1Mo-1W-0.25V耐热钢在550℃下的应力松弛曲线进行直接拟合外推的结果。可以看出，采用不同分组数据拟合外推的松弛曲线之间差异较大，时间长度越短的数据组预测的松弛曲线越偏离实验数据点，预测的8760h时的松弛应力越高，如采用t50-Z组数据预测的8760h时的松弛应力为128MPa，而t5000-Z组数据预测的松弛应力为99MPa，两者相差29MPa。与实验数据相比，短时间松弛数据的预测结果误差较大，但随着所采用数据的时间长度的增加，直接拟合外推法预测的松弛应力的误差减小，如t5000-Z组数据预测的松弛应力与实验数据十分接近。这一结果说明，利用短时间松弛实验数据进行预测时，直接拟合外推法预测的结果偏差较大，这意味着高精度预测长时间松弛应力，必须做较长时间的松弛实验，这在工程上是十分耗时、费力的。

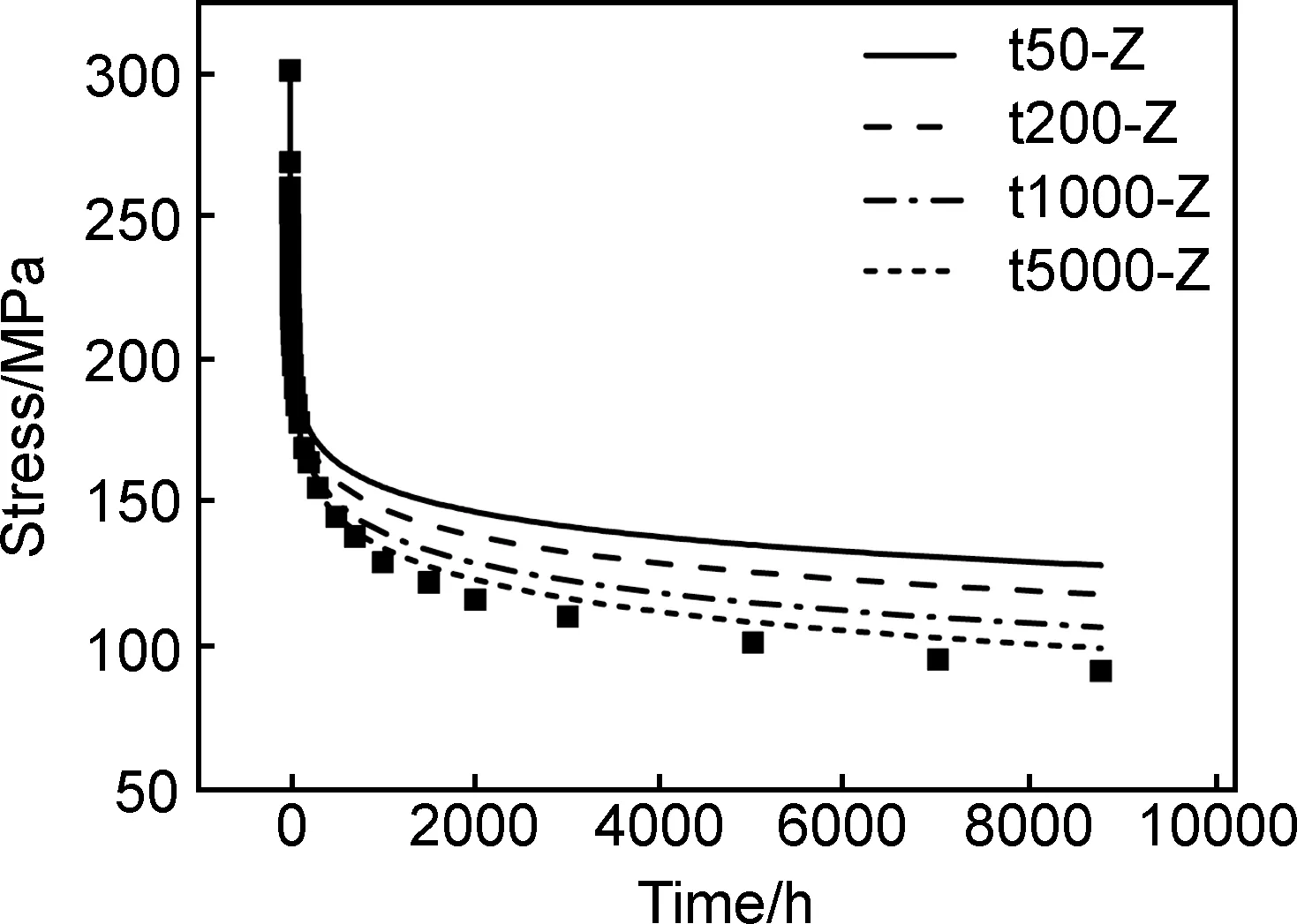
图2 直接拟合外推法得到的应力松弛曲线Fig.2 Stress relaxation curves obtained by fitting extrapolation method

2.2 直接预测模型的修正——时序参数法

通过对比不同数据组的拟合方程，发现预测结果之间的差异与拟合方程中参数a，b有关。将图2中各预测曲线的拟合方程参数与其所用数据的时间长度构建关系，如图3所示。可以看出，参数a，b与其数据组的时间长度ti之间呈现出规律性的变化。由此设想：如果预测时能够考虑拟合模型参数的变化，则能够得到更为准确的外推结果，因此，本工作提出了考虑参数变化的长时间松弛应力的预测方法——时序参数法，即

σ(ti)=σ0-atiln(btiti+1)

(2)

式中ati和bti分别为实验时间ti的函数。

式(2)表示，若想预测ti时刻的松弛应力，需要首先得到ti时间所对应的拟合方程参数ati和bti，而ati和bti可以根据如图3所示的关系进行外推得到。

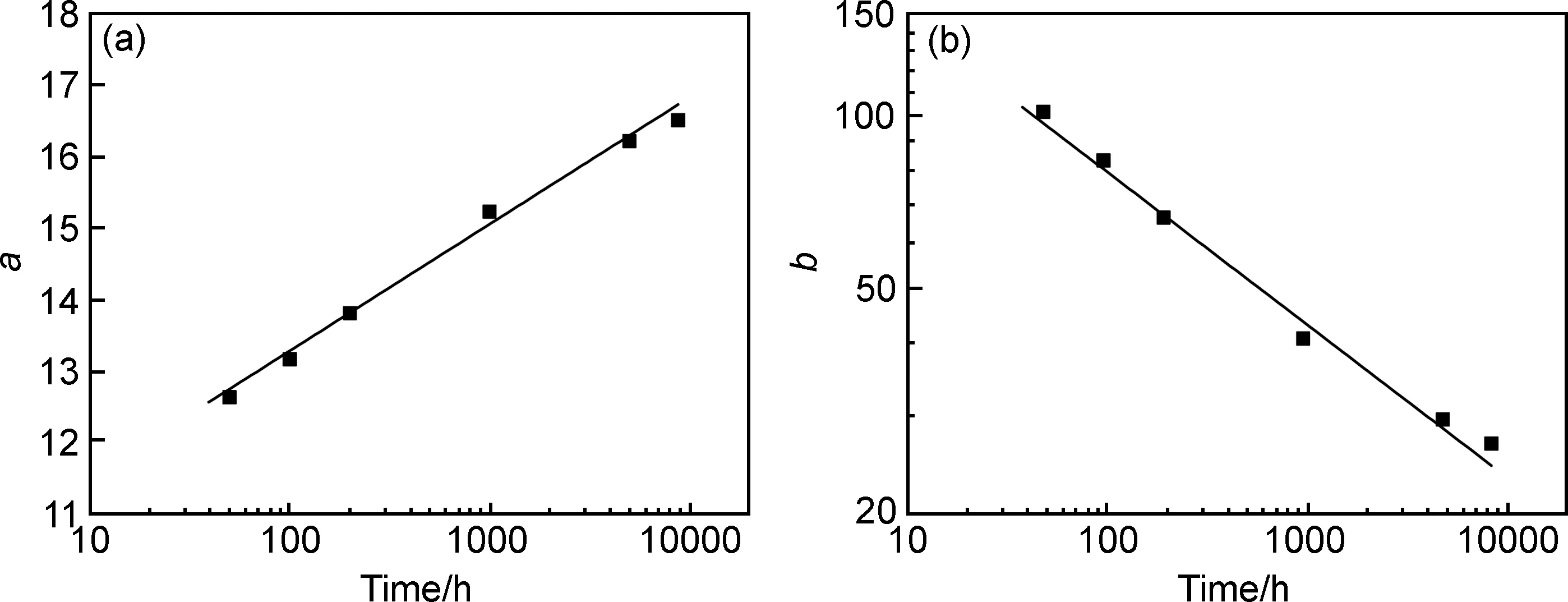
图3 模型参数a，b随时间的变化规律 (a)参数a；(b)参数bFig.3 Variation of parameter a and b with time (a)parameter a;(b)parameter b

2.3 时序参数法的验证及分析

2.3.1 在550℃实验中的验证

12Cr-1Mo-1W-0.25V耐热钢的拟合方程参数随实验时间的变化规律如式(3)，(4)所示。

ati=a1+a2lnti

(3)

(4)

为确认时序参数法预测长时间松弛应力结果的准确性，选用短时间的松弛数据来对550℃/8760h的松弛应力进行预测，预测结果与直接拟合预测的结果和实验数据分别进行比较分析，基本步骤：①参考直接预测的数据分组，时序参数法预测时的分组如表2所示。例如，t200-M表示数据时间为0～200h，与直接预测法的t200-Z数据组匹配；②对各数据组中的数据再细化分组，如将t200-M数据组分为时间更短的t20-Z，t30-Z，…，t200-Z等；③基于松弛方程(1)对再细化分组的数据进行拟合，得到相应的参数ati和bti，如t20-Z，t30-Z组数据拟合得到的a20，b20和a30，b30；④建立参数a，b与时间的关系模型。本工作在预测8760h模型参数时采用了式(3)，(4)的关系模型，是因为其为比较简单的线性关系，而且对于短时间数据符合良好，预测方法结果如图4所示；⑤根据参数a，b与时间的关系，计算所需预测时间的ati和bti值，代入式(2)中计算相应的松弛应力及预测误差。例如：要预测8760h的松弛应力，根据a-ti，b-ti的关系计算得到参数a8760，b8760，再将a8760，b8760代入式(2)中得到σ(8760)。

表2 采用时序参数法进行预测的数据组Table 2 Data group used in the prediction by timing parameter method

图5为时序参数法预测550℃/8760h松弛应力曲线及两种方法预测的550℃/8760h松弛应力误差。由图5(a)可知，不同数据段的预测结果之间相差很小，用t50-M组数据的预测结果与用t5000-M数据预测的结果仅相差10MPa，而用直接预测法进行预测时的外推结果之差却高达29MPa (图2)，由此可见，时序参数法的预测结果一致性较好。图5(b)中σP为预测松弛应力，σD为实验松弛应力。可以看出，用时序参数法进行预测的结果误差较小，精度较高，即使是用0～50h数据进行预测的结果与其实验数据之差也仅为15MPa，远低于直接拟合外推法的预测误差(37MPa)，而当时间扩展至200h时，时序参数法误差缩小至8MPa, 而直接预测的误差仍然较高，约为27MPa。

图4 参数a，b的推导 (a)参数a；(b)参数bFig.4 Deduce of parameter a and b (a)parameter a;(b)parameter b

图5 时序参数法预测550℃/8760h时松弛应力曲线(a)及两种方法预测的550℃/8760h松弛应力误差(b)Fig.5 Stress relaxation curves of 550℃/8760h predicted by timing parameter method(a) and the stress relaxation error of 550℃/8760h predicted by two methods(b)

2.3.2 其他实验条件中的验证

考虑到不同实验条件下时序参数法的适用性，对12Cr-1Mo-1W-0.25V耐热钢600℃的松弛数据也进行相同的分析处理，如图6所示。时序参数法预测600℃/8760h的松弛应力结果如图6(a)所示，预测结果与实验数据相近，不同数据组的预测结果之间的差别也不大。与550℃的结果类似，时序参数法预测结果的精度较高，特别是当用短时间数据段进行长时间松弛应力预测时，其预测精度仍然较高。

550，600℃下的预测结果表明，时序参数法在预测时对数据时间长度的依赖性要小，用相同实验时间数据进行预测时，时序参数法的预测精度比直接拟合外推更高。换而言之，用时序参数法进行长时松弛应力预测时，即使是短时的松弛数据也可以得到精度较高的结果。

2.3.3 参数a与b的物理意义

在以上的研究当中，发现公式(1)中的参数a与b与实验的持续时间分别呈现出式(3)，式(4)的关系。同时，文献[11]也指出，参数a与表观激活体积(V*)呈反比关系，而参数b与表观激活体积V*及零时刻变形速率的乘积呈正比。表观激活体积表征运动位错跨过局部障碍所扫过的面积与伯式矢量的乘积。在本工作中，参数a随着时间的递增关系意味着V*随着实验时间的持续而递减。V*的减小反映了在热激活变形过程当中，由外加应力所提供的功的降低，同时也表明越过障碍由热激活所提供能量的升高，也就是说随着实验时间的延长，试样变形越来越困难。

2.4 时序参数法在长时间松弛应力预测当中的应用

从上面的分析结果可以看出，当用松弛模型进行松弛应力外推时，模型参数的变化对结果的预测精度

图6 时序参数法预测的600℃/8760h时松弛应力曲线(a)及两种方法预测的600℃/8760h松弛应力误差(b)Fig.6 Stress relaxation curves of 600℃/8760h predicted by timing parameter method(a) and the stress relaxation error of 600℃/8760h predicted by two methods(b)

影响很大。图5(b)和图6(b)的误差分析表明，时序参数法具有更好的预测结果，因此本工作将时序参数应用于更长时间，如10000，20000，30000，50000h松弛应力的预测上，其结果如图7所示。从预测结果上看，用公式(1)直接拟合外推时(图7实心点)，采用短时间数据预测的松弛应力明显高于采用长时间数据的外推结果，如数据t200-Z预测的30000h松弛应力与t8760-Z组预测结果之差达到24MPa。而采用时序参数法时(图7空心点)，预测结果之间差异较小，t200-M预测30000h的松弛应力与t8760-M预测结果仅相差4MPa。由此可以看出，不同数据段用方程直接拟合外推的结果较为分散，预测的精度相对较低，而用时序参数法进行预测时，预测结果较为集中且精度相对较高，因此预测结果的可信性也较高。另外，直接拟合外推法即使用长时间的松弛数据进行外推，其预测效果也较用时序参数法用短时数据进行预测的结果差。

图7 两种方法预测的550℃长时间松弛应力对比Fig.7 Comparison of 550℃ long-term stress relaxation predicted by two methods

与工程上通常采用的方程直接拟合外推法相比，时序参数法是在应用松弛模型时充分考虑模型参数随时间变化的因素，预测结果误差更小。对12Cr-1Mo-1W-0.25V耐热钢不同温度的8760h应力松弛数据的分析结果表明，时序参数法在用短时间数据外推长时间松弛应力时具有较高的准确性。但是值得注意的是，不同材料之间的松弛规律可能存在差异，因此描述松弛规律的松弛模型也会有所区别，但当选定合适的松弛模型后，若想准确进行预测，必须考虑模型中参量在不同数据范围内的变化。另外，在用短时间数据推导长时间数据的过程当中，除松弛规律会发生变化以外，模型参数的变化规律也会有所不同，本工作中所采用的模型是比较简单的线性关系，在其他材料当中，变化规律可能是非线性的。除此之外，一些材料[15]在松弛过程中可能会发生微观组织的显著变化，从而导致其松弛行为发生突变，不再服从单调松弛规律，这些情况下，时序参数法的应用就存在了限制，此时不能仅依靠短时间松弛数据进行预测，也需要个别的长时间松弛数据和对时序参数法进行适当的修正。但是，对于相类似的材料，松弛规律是比较接近的，可以采用类似参数关系模型。

3 结论

(1)直接外推法在预测长时间松弛应力时的结果偏差较大，而通过本工作提出的时序参数法进行预测的差异较小，预测结果较为准确。

(2)松弛模型参数随着实验数据时间长度的增加而有规律的变化，利用这种规律性可以推导出所需预测时间的松弛方程参数，提高松弛应力的预测精度。

(3)在采用短时间松弛数据预测长时间松弛应力时，时序参数法较直接拟合外推法具有更高的精度和准确性。

[1] GUPTA I, LI J C M. Stress relaxation, internal stress, and work hardening in some bcc metals and alloys[J]. Metall Trans, 1970,1(8):2223-2230.

[2] 平修二. 金属材料的高温强度理论·设计[M].郭迁玮,李安定,徐介平，译.北京:科学出版社,1983.154.

TAIRA S. High Temperature Strength of Metallic Materials Theory and Design[M]. GUO Q W, LI A D, XU J P, translate. Beijing: Science Press,1983.154.

[3] 刘勇,尹钟大,朱景川,等. 工艺因素对TC4合金应力松弛行为的影响[J]. 材料工程,2005,(4):38-41.

LIU Y, YIN Z D, ZHU J C, et al. Influence of processing factors on stress relaxation behavior of TC4 alloy[J]. J Mater Eng, 2005,(4):38-41.

[4] 郭进全, 轩福贞, 何磊. 螺栓材料1Cr10NiMoW2VNbN的应力松弛行为及预测模型[J].核动力工程,2008,29(6):119-124.

GUO J Q, XUAN F Z, HE L. Stress relaxation performance and prediction models for bolt material of 1Cr10NiMoW2VNbN[J]. Nucl Power Eng,2008,29(6):119-124.

[5] EK C G, HAGSTRÖM B, KUBT J, et al. Prediction of the creep behaviour of polyethylene and molybdenum from stress relaxation experiments[J]. Rheologica Acta,1986,25(5):534-541.

[6] ALTENBACH H, NAUMENKO K,GORASH Y. Creep analysis for a wide stress range based on stress relaxation experiments[J]. Int J Mod Phys B,2008,22(31-32):5413-5418.

[7] 曹铁山,方旭东,程从前,等. 应力松弛方法研究2种HR3C耐热钢的高温蠕变行为[J]. 金属学报,2014,50(11):1343-1349.

CAO T S, FANG X D, CHENG C Q,et al. Creep behavior of two kinds of HR3C heat resistant steels based on stress relaxation tests[J].Acta Metall Sin,2014,50(11):1343-1349.

[8] WOODFORD D A. Advances in the use of stress relaxation data for design and life assessment in combustion turbines[J].JSME Int J A-Solid M,2002,45(1):98-103.

[9] BEDDOES J. Prediction of creep properties for two nickel-base superalloys from stress relaxation testing[J].J Strain Anal Eng, 2011,46(6):416-427.

[10] 湛利华, 王萌, 黄明辉. 基于蠕变公式的时效应力松弛行为预测模型[J]. 机械工程学报,2013,49(10):70-76.

ZHAN L H, WANG M, HUANG M H. Prediction model for aging stress-relaxation behavior based on creep equations[J]. J Mech Eng,2013,49(10):70-76.

[11] DOTSENKO V I. Stress relaxation in crystals[J]. Phys Stat Sol B,1979,93(1):11-43.

[12] DAVIS F M, DE VITA R. A three-dimensional constitutive model for the stress relaxation of articular ligaments[J]. Biomech Model Mechan,2014,13(3):653-663.

[13] GRANEK R, CATES M E. Stress-relaxation in living polymers-results from a poisson renewal model[J]. J Cheml Phys,1992,96(6):4758-4767.

[14] 董瑾. 汽轮机螺栓应力松弛行为预测的研究[J]. 华北电力大学学报,2013,40(1):84-87.

DONG J. Study on stress relaxation performance prediction for steam turbine bolts[J]. J N China Elec Power Univ,2013,40(1):84-87.

[15] OHBA T,KANEMARU O,YAGI K, et al. Long-term stress relaxation properties of NCF 800H alloy[J]. Soc Mat Sci,1997,46(1):19-24.

(本文责编：王 晶)

Stress Relaxation Behavior and Its Prediction of CrMoWV Steel

CAO Tie-shan1,CHENG Cong-qian1，ZHU Yue-mei2，ZHANG Hong-wei2，LIU Song-feng2，ZHAO Jie1

(1 School of Materials Science and Engineering,Dalian University of Technology, Dalian 116085,Liaoning,China;2 Shanghai Turbine Co.,Ltd.,Shanghai 200240,China)

The stress relaxation data up to 8760h at 550℃ and 600℃of 12Cr-1Mo-1W-0.25V heat-resistant steel were used as the object to study the method of how to accurately and effectively predict long-term relaxation stress by using short-time relaxation data. When relaxation model is used to extrapolate the long-term relaxation stress directly, it is found that the parameters of the relaxation model depend on the length of the fitted data. The time-dependent parameter model, naming as timing parameter method, is proposed to predict the long-term relaxation stress with high accuracy. By comparison of the results of timing parameter method and direct extrapolation method, timing parameter method has obvious advantages in predicting long time relaxation stress with short time relaxation data, as the timing parameter method has a more accurate prediction than that of direct extrapolation method.

stress relaxation;relaxation model;timing parameter method;prediction

国家自然科学基金资助项目(51171037，51134013)；中央高校基本科研业务费专项基金资助(DUT17RC(3)010)

2015-04-27；

2016-09-25

赵杰(1964-)，男，教授，博士，研究方向为失效分析，联系地址：辽宁省大连市大连理工大学材料馆326(116085)，E-mail:jiezhao@dlut.edu.cn

10.11868/j.issn.1001-4381.2015.000508

TG132.33

A

1001-4381(2017)05-0106-06