柔性基础准零刚度隔振系统全局性态分析

赵建学，俞 翔，柴 凯，杨庆超

（1.海军工程大学 动力工程学院，武汉 430033； 2.海军工程大学 科研部，武汉 430033）

柔性基础准零刚度隔振系统全局性态分析

赵建学1，俞 翔2，柴 凯1，杨庆超2

（1.海军工程大学 动力工程学院，武汉 430033； 2.海军工程大学 科研部，武汉 430033）

以具有柔性基础的准零刚度隔振系统为对象，建立非线性隔振系统的动力学模型，并在大参数范围内分析其分岔特性。利用点映射方法并选取多个分析平面研究系统吸引子及其吸引域等全局特性，分析周期吸引子共存现象。研究表明，准零刚度非线性隔振系统随激励力幅值的变化呈现出非常复杂的动力学特性，多处出现吸引子共存现象，周期3运动的出现使得系统已经对初始条件具有了一定的敏感性。

振动与波；准零刚度；全局性态；分岔；周期吸引子共存

准零刚度隔振系统因具有良好的低频隔振效果[1–2]，在舰船动力设备振动噪声控制领域有着广阔的应用前景。然而，非线性系统的多值性本质使得准零刚度隔振系统可能存在多个吸引子，系统运行在不同的吸引子时具有不同的隔振效果，因此有必要对准零刚度隔振系统的吸引子及其吸引域进行详细分析，这对于准零刚度隔振系统设计和基于准零刚度隔振系统的主动控制算法研究具有重要意义。

自Alabuzhev[3]提出准零刚度的概念以来，很多学者对准零刚度隔振器进行了研究工作，包括准零刚度隔振器的设计及动力学分析[4–11]。准零刚度隔振系统的动力学分析方法大致有两大类，一是求出系统近似解的定量分析法，比如谐波平衡法[5]、平均法[6]、多尺度法[7]等，分析系统动力学特性。二是可直观表示解的主要性质及特征的数值分析方法[9–11]，主要用于系统吸引子、相轨迹和相平面等性质的分析。孟令帅等设计了一种由碟形弹簧负刚度机构与线性正刚度弹簧并联的准零刚度隔振系统，分别建立了系统在简谐力和简谐位移激励下的非线性动力学方程，并运用平均法进行动力学特性研究[6]。韩彦伟建立了5阶准零刚度非线性隔振系统，并定性分析了激励幅值、阻尼比及激励频率对系统非线性动力学行为的影响，研究了系统的倍周期分岔和混沌等复杂动力学行为[9]。张月英建立了准零刚度系统的数学模型，并定性分析了简谐激励作用下准零刚度隔振系统的分岔特性[11]。

本文针对具有柔性基础的准零刚度隔振系统，建立了系统动力学模型，运用数值分析方法研究了系统在较大参数范围内的分岔特性，并利用点映射方法得到了典型参数下系统的全局性态。

1 柔性基础准零刚度隔振系统模型

舰船动力设备隔振系统基座应是具有一定机械阻抗的柔性基础，若按照经典隔振理论以绝对刚性基础来计算和分析，则会使得计算得到的隔振效果有所降低[12]。并且对于准零刚度这样的非线性系统来说，还会使得其非线性动力学特性与实际的舰船动力设备隔振系统有较大差别。为更合理地描述和分析舰船动力设备准零刚度隔振系统全局性态，首先建立具有柔性基础的准零刚度隔振系统模型。

若仅考虑柔性基础的第一阶模态（模态综合法）或者1阶基函数（里兹—瑞利法），则可将柔性基础等效为一个由弹簧和阻尼支撑的质量块，其刚度、质量分别为1阶等效刚度和一阶等效质量，阻尼则取较小的阻尼值。假设只考虑竖直方向上的振动，柔性基础准零刚度隔振系统转化为了两自由度隔振系统，如图1所示。

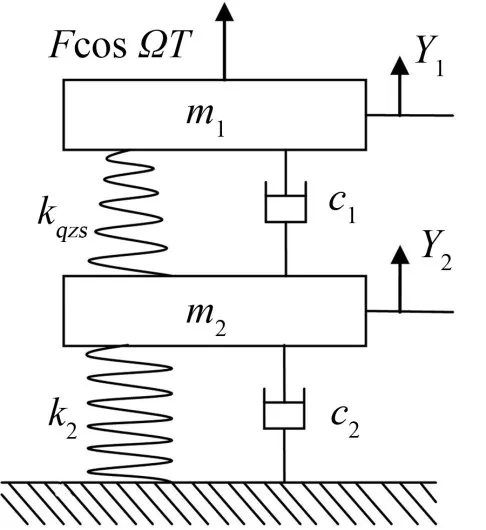
图1 准零刚度隔振系统示意图

以向上为正方向，可得

kqzs、k2分别表示准零刚度隔振器非线性刚度，基座等效刚度；c1、c2分别表示非线性准零刚度隔振器阻尼，基座等效阻尼；Y1、Y2分别表示被隔振设备位移，基座位移；m1、m2分别表示被隔振设备质量，基座等效质量；FcosΩT表示加在隔振设备上的激励。

令

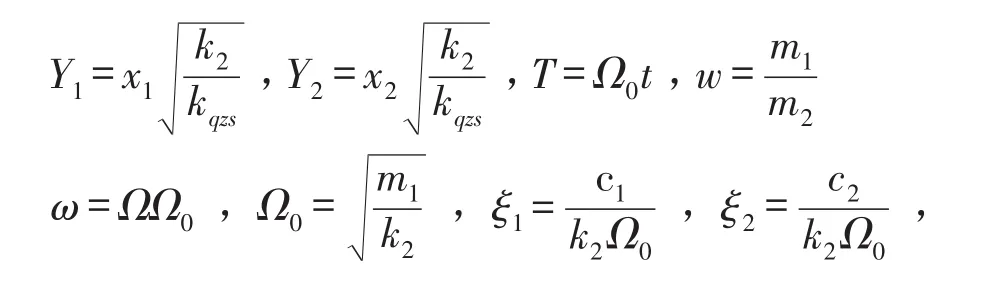
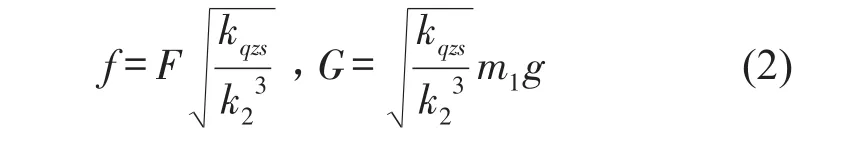
则（1）式转化为无量纲非线性系统模型

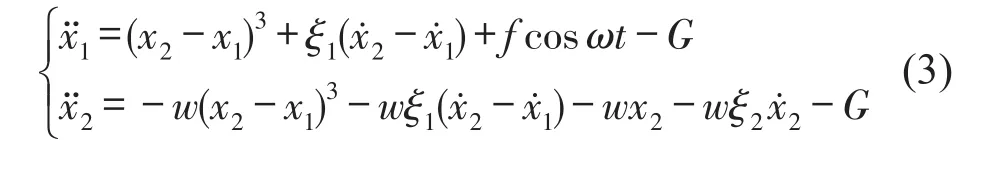
2 分岔特性分析

为获取柔性基础准零刚度隔振系统全局性态，需对其在较大参数范围内以及整个相空间中的分岔特性进行详细分析。由于篇幅所限，本文仅对系统随激励力幅值变化的分岔特性进行研究，即固定系统式（2）的激励力频率ω=1.6，而以激励力幅值f为分岔分析的控制参数。

采用延拓算法，即将在fn求得的解直接作为fn+1=fn+Δf时的初始条件。令w=0.5，G=0.1，ξ1=0.05，ξ2=0.15，取初始值为x1=0，ẋ1=0，x2=0，ẋ2=0，将f在0～50 Hz范围内向前延拓得到所有的解枝在分岔图上表示出来。

图2所示为f在0～50范围内所有的解枝，从图2可以看出系统存在周期运动（包括周期1，周期2，周期3等）、准周期运动以及混沌运动。下面分区域对系统分岔特性进行讨论与分析。

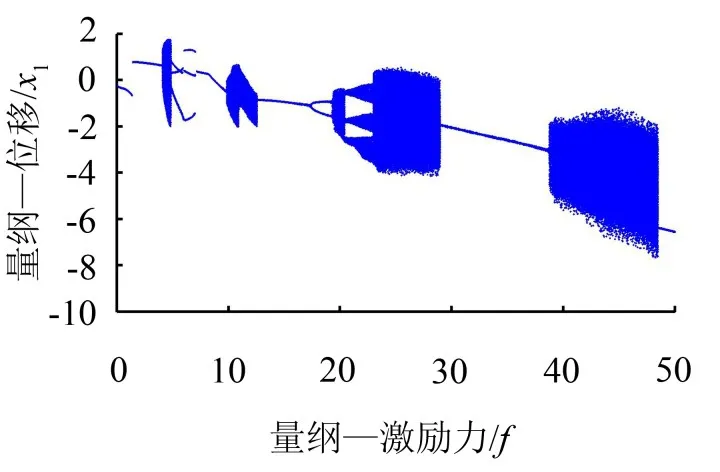
图2 系统随激励力幅值变化的分岔图(0≤f≤50)

0≤f≤5时，分岔情况如图3所示。

f＜1.43时，系统响应为周期1运动。f=1.43时，系统响应由周期1运动突变为另一个周期1运动。f=4.14时，系统响应通过Hopf分岔变为准周期运动。f=4.57时，系统进入混沌状态。f=4.86时，系统响应变为周期3运动。4≤f≤5范围内最大Lyapunov指数如图4所示。

从图上可以清楚地看到，系统处于准周期运动时，其最大Lyapunov指数为零。

5≤f≤9时，分岔情况如图5所示。f＜6.04时，系统响应仍为周期3运动。f=6.04时，系统响应由一个周期3运动变为另一个周期3运动。f=7.04时，系统由周期3运动变为周期1运动。

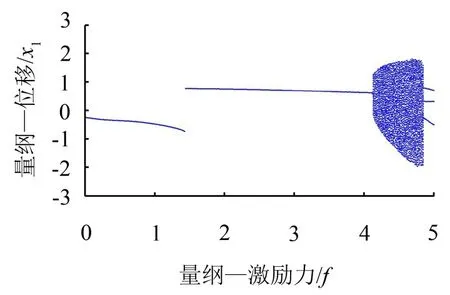
图3 系统随激励力幅值变化的分岔图(0≤f≤5)

图4 最大Lyapunov指数与分岔图(4≤f≤5)

图5 系统随激励力幅值变化的分岔图(5≤f≤9)

9≤f≤19时，分岔情况如图6所示。

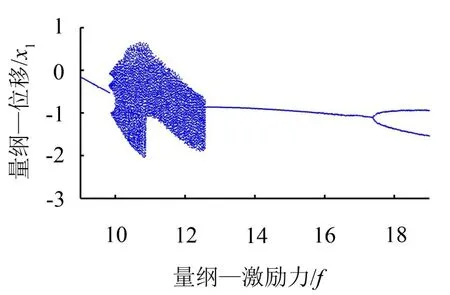
图6 系统随激励力幅值变化的分岔图(9≤f≤19)

f＜9.84时，系统响应为周期1运动。f=9.84时，系统响应由周期1运动通过Hopf分岔变为准周期运动，并于f=10.02时，系统进入混沌运动状态。f=10.88时，系统响应由一个混沌运动变为另一个混沌运动。f=12.59时，系统响应由混沌运动变成周期1运动。f=16.77时，系统响应由周期1分岔为周期2运动。9≤f≤13范围内的最大Lyapunov指数图如图7所示。可以看出，当系统处于准周期运动时，最大Lyapunov指数等于零。

图7 最大Lyapunov指数与分岔图(9≤f≤13)

19≤f≤32时，分岔情况如图8所示。

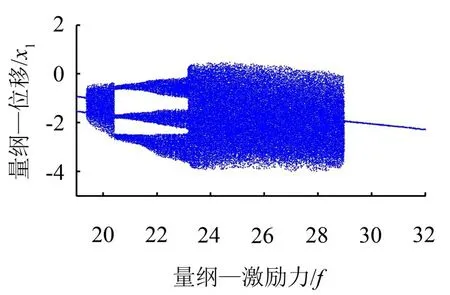
图8 系统随激励力幅值变化的分岔图(19≤f≤32)

f＜19.36时，系统响应仍为周期 2运动。f=19.36时，系统响应由周期2运动变为混沌运动。f=20.40时，系统由混沌运动变为准周期运动，并于f=23.11时变为另一个混沌运动。f=29.10时，系统响应由混沌运动变为周期1运动。19≤f≤30范围内的最大Lyapunov指数图如图9所示。可以看出，系统处于准周期运动时，最大Lyapunov指数等于零。

图9 最大Lyapunov指数与分岔图(19≤f≤30)

32≤f≤50时 ，分岔情况如图 10所示。f＜38.78时，系统响应仍为周期1运动。f=38.78时，系统响应由一个周期1运动变为混沌运动。f=48.48时，系统由混沌运动变为周期1运动。

38≤f≤50范围内最大Lyapunov指数如图11所示。可以看到，系统响应是混沌运动时，最大Lyapunov指数大于零。

图10 系统随激励力幅值变化的分岔图(32≤f≤50)

图11 最大Lyapunov指数与分岔图(38≤f≤50)

3 全局性态分析

上面详细描述了f在0～50 Hz范围内向前延拓得到的分岔图，实际上，非线性系统在多个参数区间将出现多个吸引子共存现象，为分析系统在0≤f≤50的全部吸引子共存情况，为全局性态分析提供依据，将向前延拓和向后延拓得到的分岔情况画在同一个图上，如图12所示。向前延拓表示f由小变大，向后延拓表示f由大变小。

图12 系统随激励力幅值变化的分岔图(0≤f≤50)

从图12中可以清楚地看到系统存在吸引子共存现象，且系统在混沌或准周期运动附近时，更容易出现吸引子共存。如，当f=1和f=30时，都存在两个周期1吸引子；当f=5.5和f=6.5时，都存在一个周期3吸引子和一个周期1吸引子。为进一步得到这些共存的吸引子及吸引域，利用点映射方法（PMM）进行计算。

选取f=1。由分岔图可看到，此时系统存在两个周期1吸引子，如图13(a)、图13(b)所示。

分析平面选为-2≤x1≤1，-1≤ẋ1≤2，其它初始条件固定为x2=0，ẋ2=0得到吸引子及其吸引域图。如图14(a)所示，灰色区域表示周期1运动的吸引域，白色“+”为周期1吸引子。黑色区域表示另一个周期1运动的吸引域，白色“o”表示其吸引子。

同样是选取f=1。分析平面选为-1≤x2≤1.5，-1≤ẋ2≤1，其它初始条件固定为x1=0，ẋ1=0，得到吸引子及其吸引域图。如图14 (b)所示，灰色区域表示周期1运动的吸引域，白色“+”为周期1吸引子。黑色区域表示另一个周期1运动的吸引域，白色“o”表示其吸引子。

图13 共存吸引子的相图以及Poincare映射点(f=1)

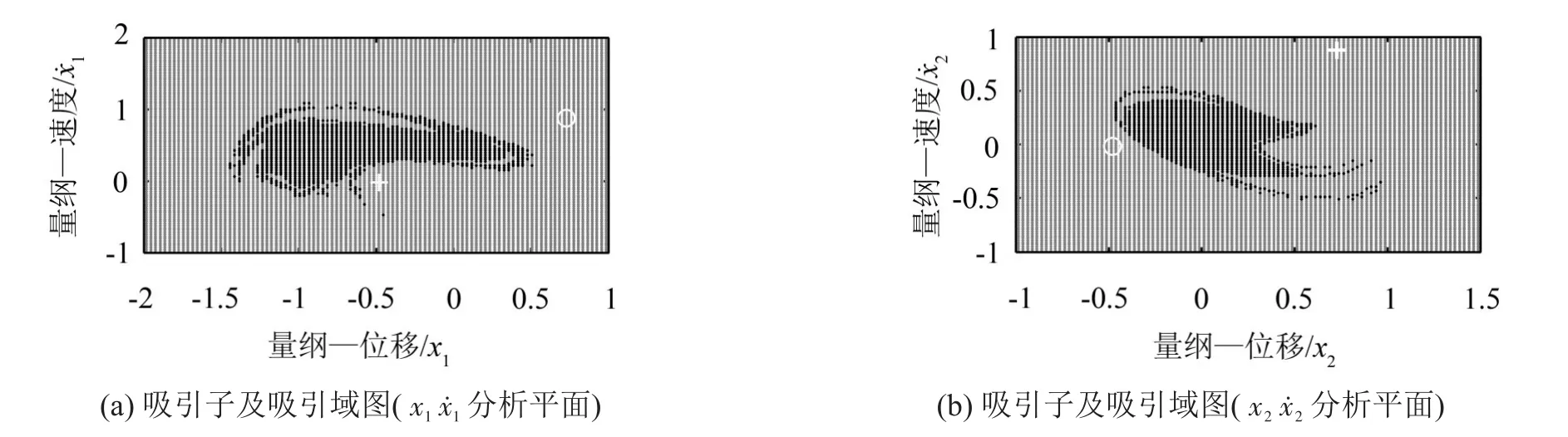
图14 吸引子及其吸引域图（f=1）

选取f=6.5。由分岔图可看到，此时系统存在一个稳定的周期3吸引子和一个周期1吸引子，如图15所示。

分析平面选为-5≤x1≤5，-18≤ẋ1≤18，其它初始条件固定为x2=0，ẋ2=0得到吸引子及其吸引域图。如图16(a)所示，黑色区域表示周期1运动的吸引域，白色“o”为周期1吸引子。灰色区域表示周期3运动的吸引域，白色“+”表示周期3吸引子。将图19(a)上黑色边框标识的区域放大，即将分析区域选为-3.5≤x1≤-3，-8.1≤ẋ1≤-5.1，得到图16(b)，可清晰地看到吸引域边界。

对比图14(a)、图16(a)，当可以看出f=6.5时，其吸引域边界比f=1时要复杂得多，两个吸引子的吸引域相互交织在一起，这说明周期3运动的出现，使得系统已经对初始条件具有了一定的敏感性。

同样是f=6.5，选取-6≤x2≤6，-15≤ẋ2≤15为分析平面，其它初始条件固定为x1=0，ẋ1=0，得到吸引子及其吸引域图。如图17所示。

黑色区域表示周期1运动的吸引域，白色“o”为周期1吸引子。灰色区域表示周期3运动的吸引域，白色“+”表示周期3吸引子。与图16(a)相比，可以看出吸引子的吸引域有很大变化。

图15 共存吸引子的相图以及Poincare映射点(f=6.5)

图16 吸引子及其吸引域图（f=6.5）

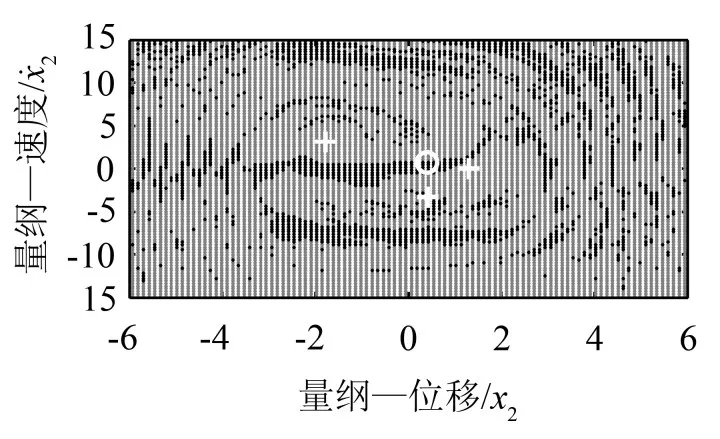
图17 吸引子及吸引域图(x2ẋ2分析平面)

4 结语

通过建立柔性基础准零刚度隔振系统模型，分析了其在较大参数区域内的分岔特性，并利用点映射方法对其吸引子和吸引域进行了分析，可以得到如下结论：

（1）以上分析表明，准零刚度非线性隔振系统随激励力幅值的变化呈现出非常复杂的动力学特性，多处出现吸引子共存现象。

（2）周期3运动的出现，使得系统已经对初始条件具有了一定的敏感性。

[1]周加喜，徐道临.一种准零刚度隔振器的特性分析与实验研究[J].振动与冲击，2014，33(11)：208-213.

[2]朱石坚，楼京俊，何其伟，等.振动理论与隔振技术[M].北京：国防工业出版社，2006.

[3]ALABUZHEV P,GRITCHIN A,KIM L,et al.Vibration protecting and mesauring system with quasi-zero stiffness [M].New York:Hemisphere Publishing Co.,Taylor& Francis Group,1989.

[4]杨庆超，楼京俊，刘树勇.准零刚度隔振系统倍周期分岔研究[J].武汉理工大学学报(交通科学与工程版），2013，37(5)：1022-1025.

[5]高双，朱翔，谌宗琦，等.基于欧拉梁的准零刚度隔振系统动力特性分析[J].中国机械工程，2016，27(21)：2869-2876.

[6]孟令帅，孙景工，牛福，等.新型准零刚度隔振系统的设计与研究[J].振动与冲击，2014，33(11)：195-199.

[7]王勇，李舜酩，程春.立方速度反馈控制的准零刚度隔振器动力学特性分析[J].振动工程学报，2016，29(2)：305-312.

[8]杨庆超，楼京俊，刘树勇.基于时延反馈精确线性化的QZS系统混沌反控制[J].武汉理工大学学报(交通科学与工程版），2015，39(6)：1212-1214.

[9]韩彦伟.一类几何非线性系统的动力学行为及应用研究[D].哈尔滨：哈尔滨工业大学，2015.

[10]丁鹏垒.车辆悬架隔振装置设计及动力学特性研究[D].长沙：湖南大学，2014.

[11]张月英.准零刚度隔振器的特性分析及实验研究[D].长沙：湖南大学，2013.

[12]朱石坚，何琳.双层隔振系统隔振效果研究[J].海军工程大学学报，2002，14(6)：6-9.

Global BehaviorAnalysis of the Quasi-zero Stiffness Vibration Isolation System with Flexible Foundation

ZHAO Jian-xue1,YU Xiang2,Chai Kai1,YANG Qing-chao2
(1.College of Power Engineering,Naval University of Engineering,Wuhan 430033,China; 2.Office of Research and Development,Naval University of Engineering,Wuhan 430033,China)

With the quasi-zero stiffness isolation system on a flexible foundation as an object,the dynamic model of the nonlinear vibration isolation system is established and its bifurcation characteristics are analyzed in a large range of parameters.The attractor and its attracting basins are investigated by using the point mapping method and selecting several analytical planes.The coexistence of periodic attractors is analyzed.The results show that the quasi-zero stiffness nonlinear vibration isolation system exhibits a very complicated dynamic behavior with the change of amplitude of the excitation force,and the coexisting of attractors.The occurrence of motion of period 3 makes the system to have some sensitivity to the initial conditions.

vibration and wave;quasi-zero stiffness;global behavior;bifurcation;coexisting of periodic attractor

O328

：A DOI编码：10.3969/j.issn.1006-1355.2017.03.004

1006-1355(2017)03-0019-05+51

2017-01-04

国家自然科学基金资助项目(51679245)；国家自然科学基金青年科学基金资助项目(51509253)

赵建学（1992－），男，河北省保定市人，硕士生，主要研究方向为振动与噪声控制。

俞翔（1978－），男，高级工程师，主要研究方向为振动与噪声控制。E-mail：:yuxiang898@sina.com