基于稀疏贝叶斯学习算法的电力线通信脉冲噪声抑制方法

薛晶，张蕊，于广亮，郑涛

（1.西安电力高等专科学校，陕西西安 710032；2.国网陕西省电力公司经济技术研究院，陕西西安710048；3.西安交通大学，陕西西安 710049）

基于稀疏贝叶斯学习算法的电力线通信脉冲噪声抑制方法

薛晶1，张蕊1，于广亮2，郑涛3

（1.西安电力高等专科学校，陕西西安 710032；2.国网陕西省电力公司经济技术研究院，陕西西安710048；3.西安交通大学，陕西西安 710049）

电力线通信脉冲噪声干扰是影响通信系统性能的主要因素之一。文中针对电力线中的脉冲噪声，采用基于稀疏贝叶斯学习算法的抗脉冲方法，将电力线信道中空子载波包含的信息用于脉冲噪声估计，通过基于正交频分复用（OFDM）的宽带电力线载波通信系统，在实际室内电压电网中，验证了算法的可行性。

电力线通信；脉冲噪声；稀疏贝叶斯；噪声抑制

随着智能电网的快速发展，尤其是中、低压配电网智能化程度的不断提高，需要可靠、高效的通信系统为电网的运行、控制和保护提供保障。电力线载波通信（power line communication，PLC）是利用电力线作为信息传输媒介的一种有线通信方式，它无需敷设新线、通信系统建设投资少，且能提供即插即用的通信服务，可作为具有大量通信节点接入的智能配电网信息交换的有效通信解决方案[1]。电力线设计之初主要考虑低频电能传输，用于携带信息的高频信号传输媒介时，会面临电力线信道的选择性衰落和电网中各种电力设备产生的噪声影响[2-3]。其中，脉冲噪声通常表现出幅度大和随机性的特点，对电力线通信噪声严重干扰，导致信息传输误码率增加。所示，抑制脉冲噪声干扰是提高电力线通信性能的有效手段之一。

当前，电力线脉冲噪声的抑制算法可以大致分为2类：参数法和非参数法。参数法，也称为非线性法，如限幅、消隐、深度限幅等。该方法基于脉冲噪声的模型假设，根据通信过程中采集的数据对模型涉及的参数进行估计，求取最优门槛值来区分脉冲噪声和非脉冲噪声，然后对接收信号进行非线性处理，达到限制脉冲噪声的目的。传统的非线性方法通过严格的数学公式推导，可获得包含最优门槛值的数学方程表达式，但是无法获取最优门槛值的解析解[4-5]。考虑到方程求解复杂，一般非线性处理的门槛值均采用数值解和经验值。为克服对经验值的依赖，有学者提出自适应门槛限幅方法。该方法利用计算机快速搜索与最低误码率相应的最优门槛值，但时间复杂度高[6]。文献[7]根据信号检测理论，将目标函数取为优化检测概率和虚报概率之差，以得到最优门槛值。利用上述参数法确定门槛值时，需要电力线脉冲噪声的先验知识，如噪声模型及相应参数。若噪声模型和参数估计结果存在一定偏差，无法得到合理门槛值，则会使通信系统性能恶化。为了减弱对噪声先验知识的依赖，文献[8]通过实验证实最优门槛值与信号峰值之间存在线性关系，如果能获取信号峰值，就可以确定门槛值。但是实际中，接收侧直接确定接收（orthogonac frequency division multiplexing，OFDM）符号峰值是不可行的，因此学者采用信号峰均功率比（peak to areraye power ratio，PAPR）的累积概率密度代替峰值来描述二者之间的相关性，从而确定最优门槛值。为了更近一步准确获取接收信号峰值，文献[9]通过量化发送信号峰值，将量化信息作为边信息传输，从而更加准确地根据峰值寻找最优门槛值；此外，非线性处理方法一般认为脉冲信号会远远大于发送信号。但是实际中发送信号（PAPR）较高时，非线性处理法会引起很大误差。因此，降低信号（PAPR），会使脉冲信号在接收信号中更加突出，从而易于找到合理门槛值。降低（PAPR）的方法如限幅、选择性映射（selective mapping，SLM）、部分传输序列（partial tronsmit sequence，PTS）以及扩频序列均可用于提高系统性能[7-8]。该类方法简单可靠，容易实现，但是这类方法在抑制噪声的同时，也会引起载波间干扰（inter-carrier interference，ICI）。

参数法在减小脉冲噪声功率影响时，使得有效信号失真。参数法需要大量训练码元符号，获取噪声模型的参数估计，并且模型参数估计与理论值之间的偏差容易直接引起性能恶化。非参数方法摆脱对先验知识的依赖，利用时域内脉冲信号的稀疏结构，直接在接收端来估计噪声信号，然后从接收信号中分离出噪声信号，从而抑制脉冲噪声。文献[12-13]利用压缩感知算法，从空子载波中估计出脉冲噪声信号。但是压缩感知算法要求满足一定条件：一个（OFDM）符号中脉冲数目不能超过由离散傅里叶变换的点数和空子载波数目共同决定的门限。实际电力线环境中，脉冲噪声随机性较强，很难满足上述条件；尽管非参数法计算复杂度高，计算时间较长，但是能够获得较好的脉冲噪声抑制效果。

本文中针对电力线脉冲，采用基于稀疏贝叶斯学习的非参数方法，利用空子载波上包含的脉冲噪声信息，估计脉冲噪声。最终从接收信号中去除脉冲噪声，达到脉冲噪声抑制的目的。并在实际室内低压电力电网中，实现了含抗噪声算法的（OFDM）宽带通信系统，验证了算法的可行性。

1 基于OFDM的宽带电力线通信

宽带电力线通信HomePlug AV协议规定使用2～30 MHz频带进行信息传输，通信速率可以达到1 Mb/s以上。OFDM技术是一种多载波调制技术，将信道分成若干正交子信道，并将高速数据信号转换成并行的低速子数据流，调制到每个子信道上进行传输。正交子信道可以通过接收端的相关技术解调，有效降低载波间干扰。同时由于每个子信道带宽小于信道相干带宽，故可以将每个子信道看作平坦衰落信道，减少码间干扰。

由于电力线信道的频率选择性，（OFDM）系统在设计子载波时，会根据信噪比估计结果，保留一部分空子载波，即在这些空子载波上不传输数据。在接收端，在这些空子载波上表现出的信息恰恰包含了数据传输过程中所受的噪声影响，因此，可以利用空子载波进行脉冲噪声的估计。

图1 基于OFDM的宽带电力线通信框图Fig.1 Diagram of OFDM based broadband power line communication system

基于（OFDM）的宽带电力线通信系统，将所使用的带宽划分成N个子载波，通过（inverse fast fourier transfor，IFFT）实现子载波分配。基于（quodrature amplitude moduiation，OFDM）的宽带电力线通信系统如图1所示。

在发送端的输入比特经历编码、加扰、交织后，经（quodrature amplitude moduiation，QAM）4映射成为{1+j，1-j，-1+j，-1-j}。经IFFT后，将复数码元符号分配在N个子载波上。在发送端，第k个子载波上的码元符号为Sk，经过（IFFT）后，输出时域信号为

为了降低由多径信道引起的码元干扰，通常在时域码元符号之前添加循环前缀（CP），通过载波环节将基带信号变换到高频带后输出。其中，编码采用卷积码（2、7，1）。在数据编码后，可能会出现连续的0或者1；加扰使得这些比特随机化，以降低在IFFT后出现较大峰值系数的可能性。交织是一种实现最大限度的改变信息结构而不改变信息内容的技术；传统上讲就是使信道传输过程中突发产生集中的错误最大限度的分散化。

在接收端，接收信号去载波、滤波后，从高频信号变为基带信号；去循环前缀相当于去掉具有码间干扰的数据。此时基带时域信号为rn。经过FFT、QAM映射、去交织、去扰和解码后，得到输出比特。接收信号表达为

其中h表示电力线信道时域脉冲响应；g表示背景噪声；服从高斯分布；e表示脉冲噪声。时域信号经过FFT后，变换到频域，则频域信号表示为

其中Hk表示信道频域传输函数；Gk表示频域背景噪声，服从高斯分布。

2 基于稀疏贝叶斯学习算法的脉冲噪声抑制方法

2.1 稀疏贝叶斯学习算法

稀疏贝叶斯学习算法首先在文献[11]中提出，后用于系数信号恢复[14-15]。通常，稀疏贝叶斯算法用于求解线性回归问题，如：

式中t∈CM是一个观测向量；Φ∈CM×N是一个过完备基（M＜N）；w∈CN是待估计的稀疏权重向量；CN（）表示高斯分布。稀疏贝叶斯学习算法中，假设w满足参数化高斯分布，即

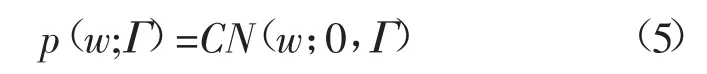
式中Γ=diag{γ}；且γ∈RN；γi是γ的第i个元素，是变量wi的方差。在此先验知识的基础上，观测向量的概率分布为

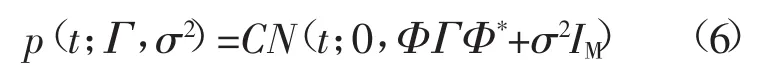
利用最大似然函数求解参数γ和σ2，在已知的观测向量和估计参数基础上，w服从高斯分布，表示为

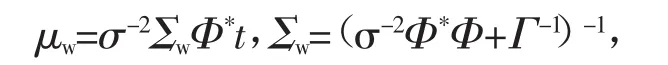
式（4）中w最大后验概率估计为均值μw，最大后验概率估计方差Σw。

2.2 基于空子载波的脉冲噪声抑制

如前所述，基于（OFDM）的电力线通信系统中，包含部分空子载波。假设空子载波的个数为M，且仅包含着噪声的信息，而剩余的N-M个子载波用于有效信号传输。利用这M个空子载波，结合式（3），接收信号的频域表达式为：

式中RI表示接收端信号；FI为信道传输函数；e为发送信号；GI为噪声干扰；其中下标（）I表示子矩阵或者子向量。对比式（4）和（8），如果令t=RI，Φ=FI,w= e，v=GI，那么两式完全一致。因此基于空子载波的信息可以用于估计脉冲噪声。具体实现过程则利用期望最大（expectation moximization，EM）方法，步骤如下

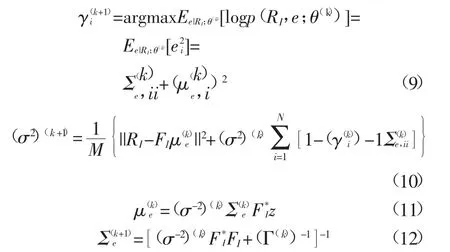
在迭代过程中，为了减少计算量，往往令背景噪声方差σ2保持不变，这样可以略去式（10）的迭代计算。计算中，需要对进行粗糙估计，赋予初值。EM算法迭代终止时，时域脉冲信号e最大后验概率估计值为μe，且对应的方差Σe中大量的元素趋近于0，这是脉冲噪声稀疏性所致。然后将时域噪声信号变换到频域，并从接收信号中分离出去。随着子载波数目不断增加，脉冲噪声估计会更加准确。

3 实验验证

为了验证算法的可行性，在实际室内低压电网中建立基于OFDM的宽带通信系统，比较采用抗脉冲算法前、后的通信性能。OFDM通信系统参数如表1所示。硬件采用NI的5412-pxi任意波形发生器和5015-pxi数字采样器，其中系统采样频率为20 MHz，带宽为5 MHz，载波频率为5.5 MHz。子载波总数为512个，其中128个为空子载波，384个子载波用于信息传输，每个子载波采用4-QAM映射。且系统实现中，采用512点（IFFT），循环前缀长度为128点。

表1 OFMD通信系统参数Tab.1 OFDM system configuration

低压电网络拓扑如图2所示。网络主干线长度为20.2 m，含有2个分支，且分支长度分别为18.1 m和2.8 m。通常，电力线通信噪声可以分为5大类：背景噪声、窄带干扰、同步周期脉冲、非同步周期脉冲和随机脉冲；也可以大致分为背景噪声和脉冲噪声。图3给出了室内低压电网实际测量得到的噪声时域波形，可以看出脉冲噪声含量非常丰富，约占整个工频周期的80%。实际测试结果如图4所示，显然，采用脉冲噪声抑制算法后，接收端星座图更容易区分，说明解码的成功率较高，通信系统的性能有所提升。

图2 电力线通信系统的网络结构Fig.2 The topology of power line communication system

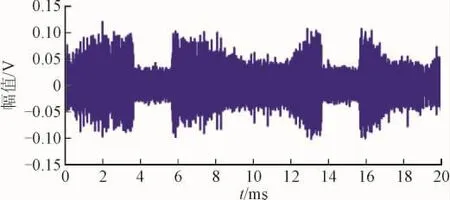
图3 实际电力线网络中采集的噪声Fig.3 Power line noise collected in real power line network

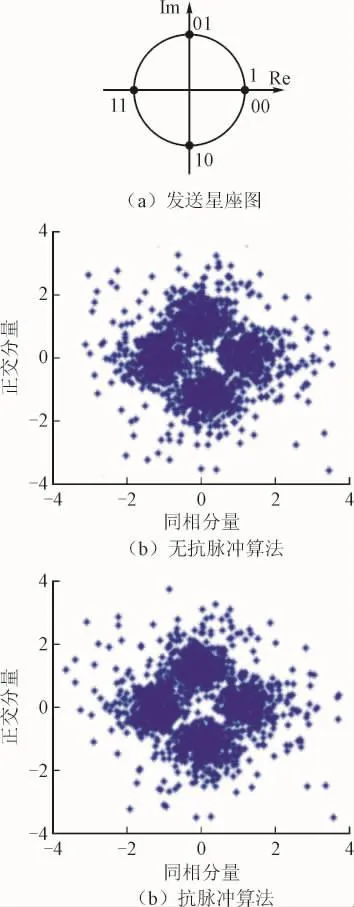
图4 通信收发端星座图Fig.4 Constellation of transmitting and receiving signals

图5 稀疏贝叶斯学习算法的性能比较Fig.5 The performance of SBL algorithm comparison

不同发送功率下，脉冲噪声抑制算法适用性验证结果如图5所示。可以看出，使用稀疏贝叶斯学习算法的通信系统性能优于传统不采用脉冲噪声抑制算法的系统。随着发送信号功率增加，BER水平逐渐降低，且2种方法之间的性能也在逐渐增大。在BER水平均为低于10-3时，2种方法发送功率分别是0.015 W和0.028 W，后者大约是前者2倍，说明（SBL）方法相对传统方法，可以获取3 dB左右的增益。在（biterror rate，BER）水平更低情况下，这2种方法对应的信号发送功率的差异增大，表明（SBL）方法相对于传统方法，可以获取大于3 dB的增益。

4 结语

针对电力线信道中丰富的脉冲噪声，本文采用了基于稀疏贝叶斯学习算法的脉冲抑制方法，并通过实际低压电网通信系统的性能验证了算法的有效性，实验结果表明，该算法能够有效抑制脉冲噪声；在发送功率较低情况下，误码率相比传统系统，没有明显的效果。但是在发送功率较高的情况下，该方法相对于传统方法，可以获取大于3dB的增益。

[1]吕英杰，邹和平，赵兵.国内低压电力线载波通信应用现状分析[J].电网与清洁能源，2010.4：33-36.LÜ Yingjie，ZOU Heping，ZHAO Bing.Analysis on application of low-voltage power line carrier communication in china[J].Power System and Clean Energy.2010.4：33-36（in Chinese）.

[2]郭昊坤，吴军基，衡思坤，等.低压电力线通信信道噪声建模及仿真[J].电力系统保护与控制，2012，7：61-66.GUO Haokun，WU Junji，HENG Sikun et al.Modeling and simulation of the noise in lou voltage power line communication channel[J].Power System Protection and Control.2012，7：61-66（in Chinese）.

[3]齐火箭，徐海宾，杨红欣.电力线宽带载波通信的干扰过滤技术[J].电网与清洁能源，2016.9：6-10+16.QI Huojian，XU Haibin，YANG Hongxin.Interference filteringtechnology forpowerline carrierbroadband communication[J].Power System and Clean Energy.2016.9：6-10+16（in Chinese）.

[4]ZHIDKOV SV.Analysis and comparison of several simple impulsive noise mitigation schemes for OFDM receivers[J].IEEE Transactions on Communications，2008，56（1）：5-9.

[5]Zhidkov SV.Analysis and comparison of several simple impulsive noise mitigation schemes for OFDM receivers[J].IEEE Transactions on Communications，2008，56（1）：5-9.

[6]Al MAWALI KS，HUSSAIN ZM.Adaptive-threshold clipping for impulsive noise reduction in OFDM-based power line communications[J].International Conference on Advanced Technologies for Communications，October，12-14，2009，43-48.

[7]NDO G，SIOHAN P，HAMON M.Adaptive noise mitigation in impulsive environment：application to power-line communications[J].IEEE Transactions on Power Delivery，2010，25（2）：647-656.

[8]ALSUSA E，RABIE KM.Dynamic peak-based threshold estimation method for mitigating impulsive noise in powerline communication systems[J]，IEEE Transactions on Power Delivery，2013，28（4）：2201-2208.

[9]RABIE KM，ALSUSA E.Quantized peak-based impulsive noise blanking in power-line communications[J].IEEE Transactions on Power Delivery，2014，29（4）：1630-1638.

[10]RABIE KM，ALSUSA E.On enhancing the performance of the DPTE-based noise cancellation method utilizing the PTS PAPR reduction scheme in PLC systems[J].IEEE International Symposium on Power Line Communications and its Applications（ISPLC），March 30-April 2，2014，334-339.

[11]RABIE KM，ALSRSA E.Efficient SLM based impulsive noise reduction in powerline OFDM communication sys tems[J].Global Communicati ons Conference（GLOBECOM），December 9-13，2013，2915-2920.

[12]MEHBOOB A，ZHANG L，KHANGOSSTAR J.Adaptive impulsive noise mitigation using multi mode compressive sensing for powerline communications[J].IEEE International Symposium on Power Line Communications and Its Applications（ISPLC），March 27-30，2012，368-373.

[13]CAIRE G，Al-NAFFOURI TY，NARAYANAN AK.Impulse noise cancellation in OFDM：an application of compressed sensing[J].IEEE International Symposium on Information Theory，July6-11 2008，1293-1297.

[14]TIPPING M，Sparse Bayesian learning and the relevance vector machine[J]J Mach Learn Res 2001，1：211-244.

[15]WIPF DP，RAO BD.“Sparse bayesian learning for basisselection”[J]IEEE Transactions on SignalProcessing，2004，52（8）：2153-2164.

Impulsive Noise Mitigation Based on Sparse Bayesian Algorithm for Power Line Communications

XUE Jing1，ZHANG Rui1，YU Guangliang2，ZHENG Tao3
（Xi’an Electric Power College，Xi’an 710032，Shaanxi，China；2.State Grid Shaanxi Electric Power Economic Research Institute，Xi’an 710048，Shaanxi，China；3.Xi’an Jiaotong University，Xi’an 710049，Shaanxi，China）

Impulsive noise is one of the key impacts on power line communication performance.This paper focuses on the suppression of impulsive noise，where the noise mitigation method based on sparse Bayesian learning algorithm is adopted.Besides，the simulation is also conducted in the real broadband orthogonal frequency division multiplexing（OFDM）power line communication system to verify the performance of this method.

power line communication；impulsive noise；sparse Bayesian learning algorithm；noise suppression

2017-02-13。

薛 晶（1982—），硕士研究生，讲师，主要研究方向为电力系统继电保护及自动化、电力系统通信。

（编辑 张晓娟）

高等学校博士学科点专项科研基金（201302011 20008）。

Project Supported by the Fund for the Doctoral Program of Higher Education of China（20130201120008）.

1674-3814（2017）04-0087-05

TM73

A