基于改进纵横交叉算法的电力系统多区域环境经济调度
2017-06-27黄强李锦焙孟安波王朗陈思哲
黄强,李锦焙,孟安波,王朗,陈思哲
(广东工业大学自动化学院,广东广州 510006)
基于改进纵横交叉算法的电力系统多区域环境经济调度
黄强,李锦焙,孟安波,王朗,陈思哲
(广东工业大学自动化学院,广东广州 510006)
随着节能环保受到日益重视,电网经济调度需同时考虑燃料成本和污染排放2个目标。电力系统多区域环境经济调度是一个复杂的非凸多目标问题,迄今未得到很好解决。基于NW小世界提出了一种新颖的改进纵横交叉算法(NWCSO)。采用容量可动态调整的外部存档集合存储当前Pareto最优解,利用Pareto占优策略确定个体最优位置,进而根据粒子拥挤距离确定全局最优位置。将NWCSO算法应用于16机组4个区域测试系统进行仿真计算,结果表明该算法在解决该多区域多目标问题方面具有优越性。
多区域环境经济调度;NWCSO算法;Pareto
在电力市场背景下,由于每个地区在发电成本方面的特殊性和负载模式的差异性,使得电网可以通过实施多区域经济调度减少生产成本。电力系统多区域经济调度是用来确定最优发电计划和潮流交换的一种方式,其目的是在满足所有地区各种限制的前提下最大限度地减少总的燃料成本[1-3]。传统的多区域经济调度往往把发电成本作为唯一的评价指标,但是为了应对越来越严重的环境问题,仅把发电机燃料费用最少作为多区域经济调度方案唯一评价指标明显不符合绿色经济的发展要求,这就要求电力系统多区域经济调度的重心也应由仅考虑经济因素的单目标调度转向同时考虑经济、环境因素的多目标调度,这就是电力系统多区域环境经济调度(MAEED)。
MAEED问题是一个非线性、非凸、高维的多目标优化问题(multi-objective optimization problem,MOP),解决这类问题的关键在于如何合理处理燃料费用和污染排放这2个相互冲突目标。解决多目标问题的传统方法有约束条件法[4]和权系数法[5]等。这些方法的主要思想是将多目标问题转变为单目标问题,然后利用传统经济调度方法进行求解。这些方法在一定程度上可以解决多目标问题。这种方法的缺点在于:需要进行大量的实验才可以确定各个目标的权系数,不利于提高效率。文献[6]提出采用混沌遗传混合优化算法解决环境/经济负荷调度,由于该方法采用了权系数法将多目标问题转变成为单目标问题进行求解,不利于做出科学决策。
近年来,人工智能优化算法被广泛应用到解决EED问题中,将互相冲突的燃料费用函数与污染气体排放量函数同时进行优化。文献[7]提出了改进非劣排序遗传算法(non-dominated sorting genetic algorithm-II,NSGA-II)用于解决多目标问题,通过对非劣解进行快速排序,大大提高了算法解决多目标问题的效率和精度。但是NSGA-II采用的是遗传算法的种群更新方式,所以该算法具有天然的收敛不稳定、早熟等缺点。文献[8]提出多目标粒子群算法(multi-objective particle swarm optimization,MOPSO)求解多目标问题,通过粒子群算法解决多目标问题虽然可以提高求解速度,但是对于求解具有高维、非凸、非线性等复杂的多目标问题时,粒子群算法容易陷入局部最优。
纵横交叉算法(crisscross optimization algorithm,CSO)[9]算法在解决单目标优化问题中已被证实具有良好的效果,例如文献[10]采用CSO算法解决多约束大规模热电联产经济调度问题。文献[11]采用CSO算法解决考虑阀点效应的大规模动态经济调度问题。文献[12-13]将CSO算法应用于求解多目标问题,并取得了不错的效果。同时也注意到,虽然基本纵横交叉算法(CSO)在处理复杂的非凸、高维度问题时,其收敛准确度方面表现良好,但由于CSO算法在进行纵向交叉时采用了随机更新种群的方式,这样的更新方式会破坏种群的整体性和多样性。为了解决这个问题,本文提出采用NW小世界网络改进原始的CSO算法,这就使得改进后的CSO算法在进行种群更新的时候仅在当前邻域内进行更新,这种更新方式不仅提高了算法的全局搜索能力,而且有利于保持种群的完整性和多样性。
1 多区域环境经济调度问题数学模型
MAEED问题是一个多目标、非凸、高维的优化问题,如何在满足各个约束条件的前提下,对各个区域以及全体发电机组的费用和排放这2个目标同时进行优化,并取得满意的折中解是解决该问题的核心,问题的描述如下。
1.1 目标函数
1)燃料费用函数。多区域经济调度要求合理分配各机组的有功出力来满足系统内各个区域以及系统总负荷需求。其费用函数为
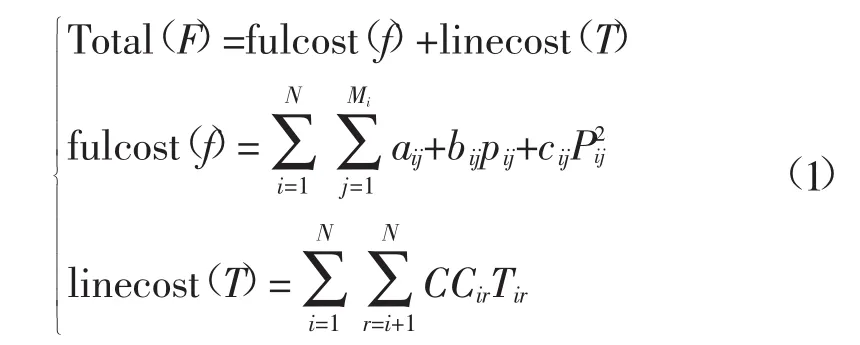
式中:Total(F)为系统总费用;fulcost(f)为系统总的燃料费用;linecost(T)为联络线传输费用;aij、bij、cij分别是第i个区域第j台发电机的燃料费用系数;Tir、CCir分别是从第i个区域传输到第r个区域的功率和费用系数;Pij是第i个区域第j台发电机的实际出力;Pminij是第i个区域第j台发电机的最小出力;M和Mi分别是所分的区域个数和第i个区域所拥有的发电机台数。
2)污染气体排放函数。系统的污染气体排放量目标函数可写为
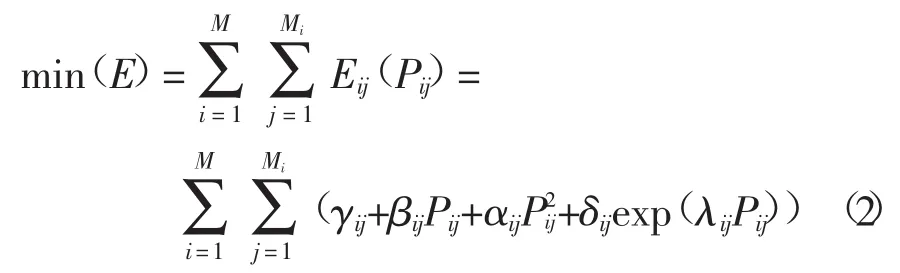
式中:αij、βij、γij、δij和λij分别是第i个区域的第j台发电机的排放系数。
1.2 约束条件
1)功率平衡约束。系统中各个区域的火电机组出力应能满足该区域的负荷需求,以及系统所有火电机组出力应能满足系统总的负荷要求。功率平衡约束可表示为

式中:Pload是系统总的负荷要求;Ploadi是第i个区域的负荷要求;Tir是从区域i传输到区域r的有功功率。
2)机组运行约束。各发电机组必须运行在其有功出力的上下限以内,可表达为

3)联络线有功功率传输约束。为了保证联络线可以长期稳定安全工作,联络线传输的功率应当控制在合理范围内,所以从区域i到区域r的联络线的实际传输功率Tir不应超过联络线的传输能力,应满足:
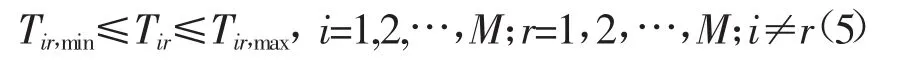
式中:Tir,min和Tir,max分别是从区域i传输到区域r的最小和最大功率,特别当功率从区域i传输到区域r时,Tir为正数,反之为负数。
1.3 多目标优化问题目标函数
目前,实际问题的优化往往涉及到多个优化目标,称为多目标优化问题(MOP),可以作如下表述:在满足系统所有约束以及需求的条件下,确定在可行域中由决策变量组成的解,使得多个目标函数组成的向量最优。MOP问题的数学模型为
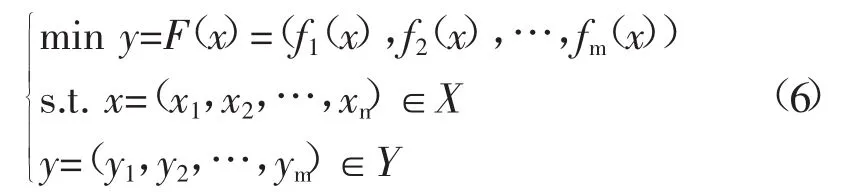
式中:X为n维的可行域决策向量空间;Y为m维的优化目标向量空间;函数F(x)为将决策向量X映射到优化目标的向量。
2 NW小世界纵横交叉算法
2.1 NW小世界网络
目前比较常用的小世界网络模型主要有WS小世界模型[14]和NW小世界模型[15]。NW小世界模型采用随机化加边的方式,克服了WS小世界模型在生产小世界网络过程会产生孤立节点的缺陷,提高了网络的连通性。
2.2 纵横交叉算法(CSO)
纵横交叉算法(CSO)是一种最近发展的群优算法,主要由横交叉操作、纵交叉操作和竞争操作组成。算法的横向交叉操作提高该算法的全局认知能力,同时,纵向交叉操作提高该算法的自身认知能力,正是由于2种极具特色的交叉方式使得算法在寻找全局搜索能力和收敛速度方面,相比其他启发式算法在解决优化问题方面表现更好,特别是在求解多峰函数和旋转函数等复杂模型时,具有巨大的优势。
2.3 基于Pareto最优的NWCSO算法解决MAEED问题
本文采用NW小世界网络改进CSO算法用于解决多区域多目标经济调度问题,其算法流程图如图1所示,基于Pareto策略的NWCSO算法解决多区域多目标的详细步骤如下。
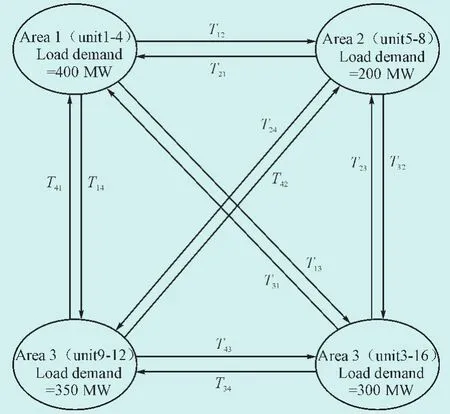
图1 16机组系统负荷分布图Fig.1 Four area,16-unit system under study
2.3.1 初始化种群
对于拥有N个区域,每个区域拥有Mi台发电机的多区域多目标问题的初始化采用如式(7)方式进行初始化。
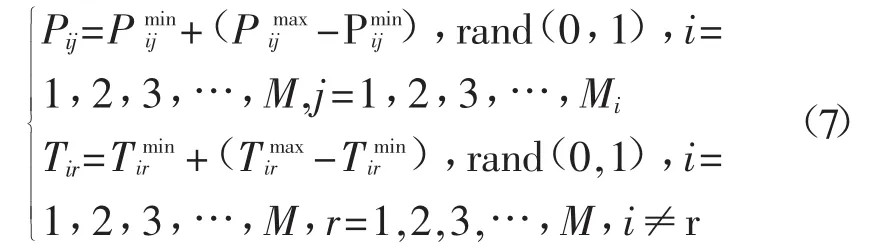
适应度函数:
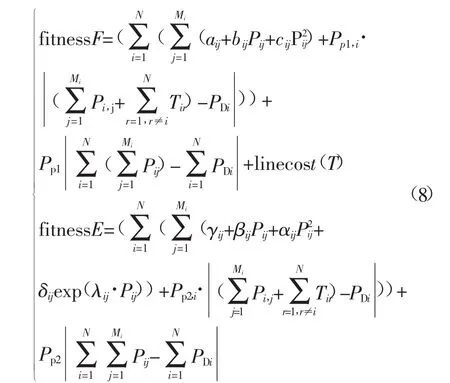
式(8)分别是发电成本和环境排放的适应度函数,其中,PDi是系统的第i个区域的负荷要求,Pp1,i和Pp1和分别是费用适应度函数的第i个区域的惩罚系数和系统总的惩罚系数,Pp2,i和Pp2分别是环境适应度函数的第i个区域的惩罚系数和系统总的惩罚系数。惩罚系数用于惩罚经过更新后产生的机组出力违背功率平衡的情况。
2.3.2 生成小世界网络
1)构造一个粒子相互连接的小世界网络。设种群中有n个粒子,在优化过程中种群中的粒子在网络中代表一个个节点,对每个节点从1~n编号,按编号顺序构成一个圆,设每个粒子的度为k(k为偶数),则每个节点与左右两边各有k/2个相连的节点。例如,若k=4,则节点1即与节点2,3,n和(n-1)相互连接;节点2即与节点3,4,1和n连接;…;依次对所有节点进行连接,直到全部的节点都完成连接[16]。
2)每个粒子以概率p进行随机加边的完成粒子之间的连接,这种随机加边的机制有利于增加优秀粒子的信息传播。设定的随机概率p随着迭代次数增加而增大,每个节点的邻居越来越多,直至达到最大迭代次数时p=1,即构成了一个完全连接矩阵。概率p公式为:
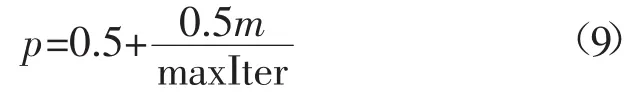
式中:m和maxIter分别是当前迭代代数和最大迭代代数。
3)横向交叉操作。该操作是在种群中2个不同的父代个体粒子相同维之间进行的1种算数交叉。对于NWCSO算法中的横向操作的具体实现如下:首先把对应领域内的粒子划分为k/2对(k为NW小世界网络当前的度),对应领域内的粒子两两配对。其次把配对后的粒子进行横向交叉操作。将横向交叉产生的子代与对应领域父代粒子合并在同一个集合内,根据非劣解排序优原则对集合内的粒子进行排序,取该集合的前一半粒子作为纵向交叉的父代粒子。采用式(10)进行横向交叉操作。
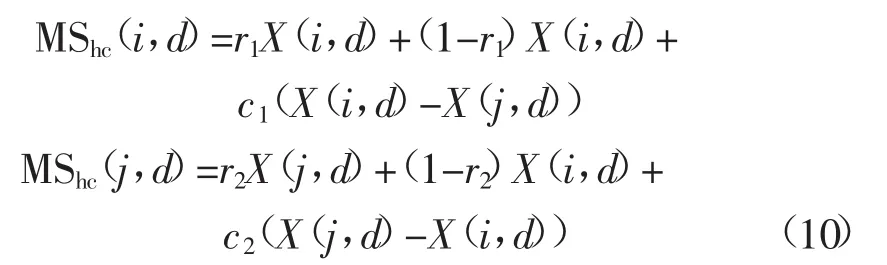
式中:r1、r2是[0,1]之间的随机数;c1、c2是[-1,1]之间平均分布的随机数;X(i,d)、X(j,d)分别是父代种群中个体粒子X(i)和X(j)的第d维;MShc(i,d)和MShc(j,d)分别是X(i,d)、X(j,d)通过横向交叉产生的第d维子代。
2.3.3 纵向交叉操作
纵向交叉是对种群中一个粒子的2个不同的维度之间进行的一种算数交叉。这种交叉方法可以促使陷入局部最优的粒子摆脱出来,增加种群的多样性。结合NW小世界网络思想的CSO算法纵向交叉操作如下:首先对对应领域内的所有粒子的维度D随机分成D/2对。其次分别对该领域内的每个粒子不同的2个维度进行纵向交叉操作。根据式(11)进行纵向交叉。将纵向交叉产生的子代与对应领域父代粒子合并在同一个集合内,根据非劣解排序原则对集合内的粒子进行排序,取该集合的前一半种作为下一次迭代的父代粒子。

式中:r∈[0,1];MSvc(i,d1)是个体粒子X(i)的第d1维和第d2维通过纵向交叉产生的第d1维后代。
2.3.4 对非劣解进行排序和选择
1)非劣解排序原则。首先,对子代个体根据Pareto支配准则与父代个体进行竞争,根据竞争后产生的新种群而形成临时种群设为A,种群A的规模介于M~2M(其中M为初始种群规模)之间。其次对种群A的粒子进行排序:首先根据帕累托占优原则找出种群A中的所有非劣解,赋予其优劣等级为1。再次对种群A剩余个体按照帕累托占优原则找出非劣解,这部分非劣解的优劣等级为2;不断重复上述步骤使得种群A所有的个体都具有相应的优劣等级。最后计算每一个个体与同级别相邻2个个体之间的拥挤距离,计算方法如式(12),当优劣等级相同的时候根据拥挤距离由大到小对矩阵A中的个体进行排序,选择前M个个体作为新的父代种群。

式中:L(i)为解的拥挤距离;f(i+1)p和f(i-1)p为解(i+1)和解(i-1)的第p个目标函数值个分别为第p个目标函数的最大、最小值;n为目标函数的总个数。
2)选取Pareto折中解。求解多目标优化问题的难点之一是:在一个由非劣解构成的Pareto最优解集内如何选择一个折中解。本文引入了模糊理论来对获得的Pareto最优面解集选择折中解[12]。根据式(13)来计算每个决策变量的隶属度函数:

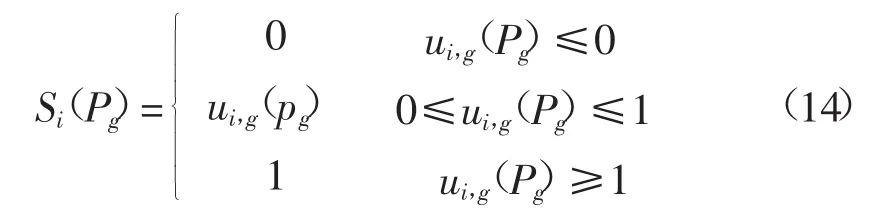
当Si(Pg)=0时解的质量较差;当Si(Pg)=1时质量最高。设有n个目标函数,m个Pareto最优前沿解,归一化后,解g的满意度计算为
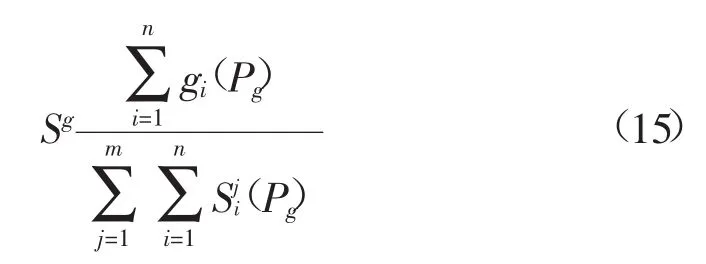
Pareto最优前沿解集中满意度最大的解即为多目标优化问题的折中解。
3 算例仿真分析
本文仿真软件采用MATLAB2012b,运行环境为惠普Paviliong4(CPU为corei3M370,2.4GHz,内存2GB)。
本文将MONWCSO算法应用到16机组电力系统的多区域环境经济调度,系统模型考虑了联络线传输费用,该系统分为4个区域,每个区域的机组数量4台,总的负荷需求为1 250 MW,其中每个区域的负荷需求以及机组分布如图2所示,机组费用参数以及各个区域之间功率传输费用系数源于文献[17],机组的排放参数源于文献[18]。

图2 基于Pareto NW小世界算法解决MAEED问题流程图Fig.2 Flowchart of NW small world crisscross optimization algorithm
本文参数设置为:种群大小N=100、最大迭代次数maxgen=1 000、纵向交叉率Pv=0.8和外部存档容量为Nc=60个。本文算法所得结果与GBABC算法的结果进行对比分析。
发电机组出力,各联络线传输功率和各区域功率平衡如表1所示。由表2可知,当以燃料成本污染气体排放最小为目标时,NWCSO算法的优化结果分别为7 336.753 7$/h和9 786.530 3 t/h,该调度结果优于GBABC算法的优化结果。图4和5是NWCSO算法对费用、环境分别进行单目标优化的收敛图。由图3、图4可知,无论是对费用单目标还是对环境单目标进行优化,NWCSO算法都能比较快的收敛到最优值。根据以上分析可以得出NWCSO算法具备良好的全局收敛能力和收敛速度。
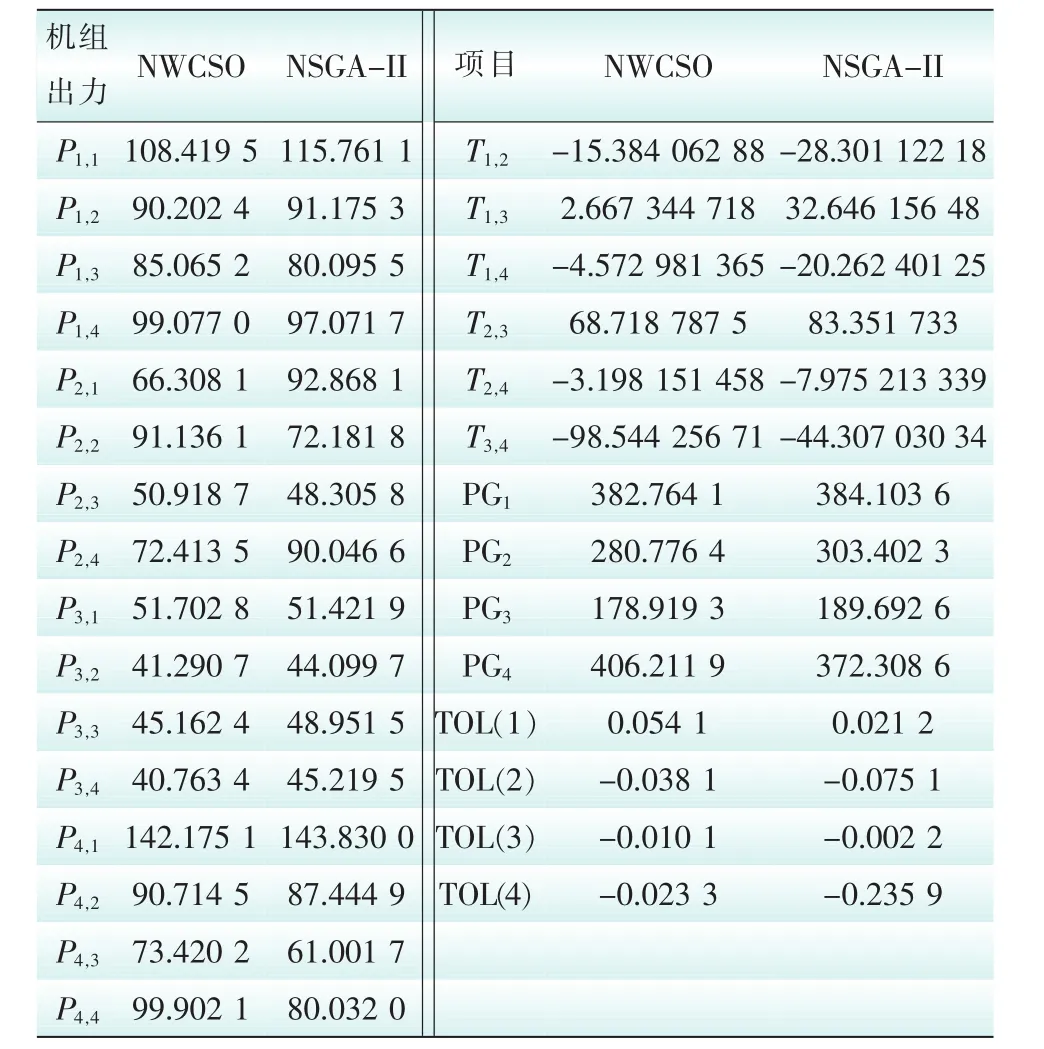
表1 最优折中调度方案Tab.1 power output for 16-units system MW
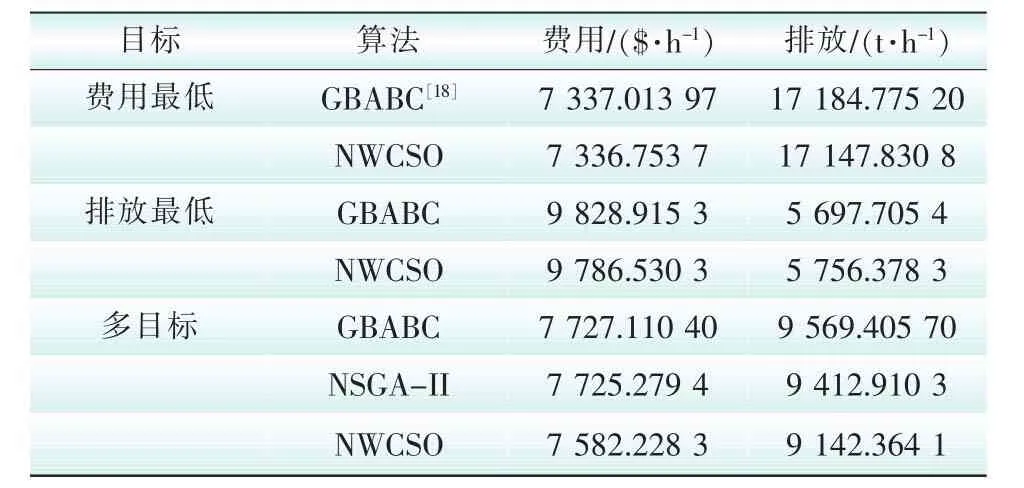
表2 极端值和最优折中解比较Tab.2 Comparison of the extreme value and best compromise solutions
采用NWCSO算法选取的折中解分别为7 582.228 3$/h和9 142.364 1 t/h。根据文献 [18],算法GBABC对该系统进行多目标优化时,成本和排放分别是7 727.110 40$/h和9 569.405 70 t/h,结合表2NWCSO算法的折中解,无论是费用折中解还是排放折中解,NWCSO算法比NSGA-II算法和GBABC算法都具有非常明显的优势,这足以表明NWCSO算法具有更高的求解精度。NWCSO算法和NSGA-II算法求解该优化问题得到的Pareto前沿图如图3所示,将NWCSO算法和NSGA-II算法的帕累托前沿和文献 [18]提供GBABC的帕累托前沿图,可以看出,NWCSO算法的帕累托前沿显得更为完整,其分布范围更大,分布更加均匀,曲线更加光滑,能够给决策者提供更优和更全面的方案供其参考。虽然NSGA-II算法也可以得到比较完整的帕累托前沿图,但是该算法在计算精度方面显然不如NWCSO算法。这也从另外一个方面证明NWCSO算法在解决多目标问题具有很好的效果。
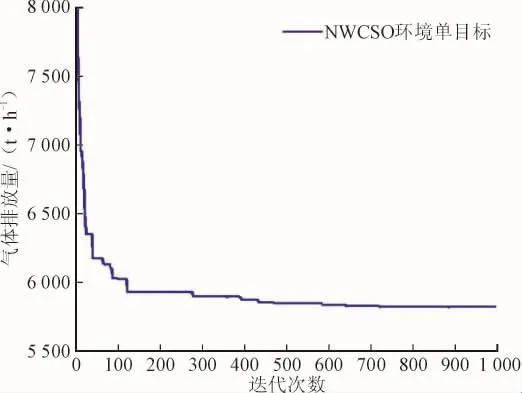
图3 污染气体排放最小的收敛特性Fig.3 Convergence of minimum emissions function
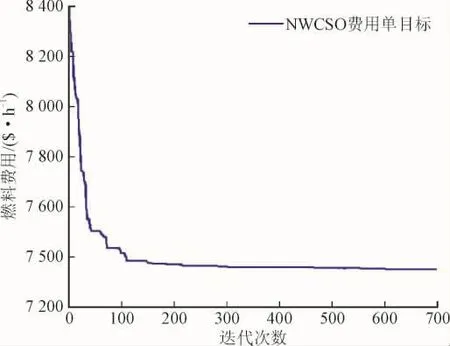
图4 燃料费用函数最小的收敛特性Fig.4 Convergence of minimum fuel cost function
4 结论
本文对NWCSO算法以及该算法在计及风电场多场景的配电系统中的应用进行了仿真,结果表明,MONWCSO算法是一种新近发展起来的多目标优化算法,由于该算法利用双交叉寻优机制对解空间进行搜索,使其具有很好的收敛速度和全局寻优能力。本文将MONWCSO算法应用于多区域电力调度领域,主要做了以下工作:
提出了基于 NWCSO的多目标多区域环境经济调度算法。该算法采用NW小世界网络对基本的CSO算法进行改进,使得算法在更新种群的时候保持种群多样性,进而提高了算法的计算精度,获得更好的MAEED问题的调度方案。
针对16机组4个区域的测试系统,采用MONWCSO算法进行多区域环境经济调度计算。通过对比GBABC算法,均取得了更小的燃料费用和排放值,所得到的Pareto前沿分布更为均匀广泛,并且能够取得更好的折中解。
结果表明NWCSO算法在折中解、Pareto前沿的完整性、以及Pareto最优解的质量等方面,均优于文献中其他智能优化算法。
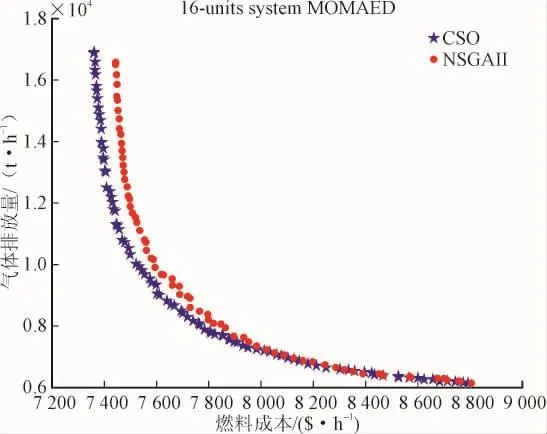
图5 NWCSO和NSGA-II算法最优Pareto前沿图Fig.5 Pareto optimal front using NWCSO and CSO algorithm
[1]郑晓菁.基于人工蜂群优化法的多区域电力系统经济调度[J].计算机工程与科学,2015,37(8):1533-1539.ZHENG Xiaojing.Multi-area economic dispatch of power system based on artificial bee colony optimization[J].Computer Engineering and Science,2015,37(8):1533-1539(in Chinese).
[2]BASU M.Teaching-learning-based optimization algorithm for multi-area economic dispatch[J].ENERGY,2014,68(8):21-28.
[3]BASU M.Artificial bee colony optimization for multi-area economic dispatch[J].International Journal of Electrical Power&Energy Systems,2013,49(9):181-187.
[4]杨柳青,林舜江,刘明波,等.考虑风电接入的大型电力系统多目标动态优化调度 [J].电工技术学报,2014,29(10):286-295.YANG Liuqing,LIN Shunjiang,LIU Mingbo,et al.Multi-objective dynamic optimal dispatch for large-scale power systems considering wind power penetration[J].Transactions of China Electrotechnical Society,2014,29(10):286-295(in Chinese).
[5]PANDIT N,TRIPATHI A,TAPASWI S,et al.Static/dynamicenvironmentaleconomicdispatchemployingchaoticmicro bacterial foraging algorithm[J].Swarm Evolutionary and Memetic Computing,2011(7076):585-592.
[6]王欣,秦斌,阳春华,等.基于混沌遗传混合优化算法的短期负荷环境和经济调度[J].中国电机工程学报,2006,26(11):128-133.WANG Xin,QIN Bin,YANG Chunhua,et al.Short term environmental/economic generation scheduling based on chaos genetic hybrid optimization algorithm[J].Proceedings of The Chinese Society For Electrical Engineering,2006,26(11):128-133(in Chinese).
[7]DEB K,PRATAP A,AGARWAL S,et al,A fast and elitist multi-objectivegenetic algorithm:NSGA-II[J].IEEE Trans on Evolutionary Computation,2002,6(2):182-197.
[8]NARIMANI M R,AZIZIPANAH ABARGHOOEE R,ZOGHDAR MOGHADAM SHAHREKOHNE B,et al.A novel approach to multi-objective optimal power flow by a new hybrid optimization algorithm considering generator constraints and multi-fuel type[J].Energy,2013,49(1):119-136.
[9]MENG A,CHEN Y,YIN H,et al.Crisscross optimization algorithm and its application[J].Knowledge-Based Systems,2014,67(4):218-229.
[10]MENG A,MEI P,YIN H,et al.Crisscross optimization algorithm for solving combined heat and power economic dispatch problem[J].Energy Conversion And Management,2015,105(9):1303-1317.
[11]MENG A,HU H,YIN H,et al.Crisscross optimization algorithm for large-scale dynamic economic dispatch problem with valve-point effects[J].ENERGY,2015,93(2):2175-2190.
[12]孟安波,李专.采用多目标纵横交叉算法的电力系统动态环境经济调度[J].电力系统保护与控制,2016(2):109-115.MENG Anbo,LI Zhuan.Dynamic environmental economic dispatch of power system adopting multi-objective crisscross optimization algorithm[J].Power System Protection and Control,2016(2):109-115.
[13]李专,陈智慧.采用分式规划与纵横交叉算法的环境经济调度[J].广东电力,2015(9):85-91.LI Zhuan,CHEN Zhihui.Environmental and economic dispatching using fractional planning and crisscross optimization algorithm[J].Guangdong Electric Power,2015,(9):85-91(in Chinese).
[14]WATTS D J,STROGATZ S H.Collective dynamics of 'small-world’networks[J].NATURE,1998,393(6684):440-442.
[15]NEWMAN M,WATTS D J.Renormalization group analysis of the small-world network model[J].Physicsletters:A,1999,263(4-6):341-346.
[16]孟安波,岳龙飞,邢林华,等.基于NW小世界的量子进化算法在无功优化中的研究[J].中国电力,2015,48(1):107-114.MENG Anbo,YUE Longfei,XING Linhua,etal.Research on reactive power optimization using quantum evolutionary algorithm based on NW small world model[J].Electric Power,2015,48(1):107-114(in Chinese).
[17]FESANGHARY M,ARDEHALI M M.A novel metaheuristic optimization methodology for solving various types of economic dispatch problem[J].Energy,2009,34(6):757-766.
[18]SECUI D C.The chaotic global best artificial bee colony algorithm for the multi-area economic/emission dispatch[J].Energy,2015,93(2):2518-2545.
(编辑 董小兵)
Improved Crisscross Optimization Algorithm for theMulti-Area Economic/Emission Dispatch
HUANG Qang,LI Jinbei,MENG Anbo,WANG Lang,CHEN Sizhe
(School of Automation,Guangdong University of Technology,Guangzhou 510006,Guangdong,China)
With increasing emphasis on energy conservation and environmental protection,the fuel cost and emission should be both taken into consideration in the economical dispatch in the power grid.The multi-area economic/emission dispatch(MAEED)is a complex non-convex multi-objective problem,which has yet to be well addressed.This paper proposes a novel NW small world network based on the crisscross optimization algorithm(NWCSO)for addressing the MAEED problem.The Pareto optimal solution is stored in an external set which is dynamically adjusted by the capacity.The personal best position is determined by using the Pareto dominant strategy and the global optimal position is identified by the crowding distance between particles.The NWCSO approach is validated on a test system consisting of 16 units with four areas considered.The scheduling scheme shows that the algorithm is both feasible and effective in solving the MAEED problem.In addition,the results show that NWCSO algorithm obtains better solution quality than other algorithms in the literature.
Multi-area economic/emission dispatch;NW smallworldimprovementcrisscrossoptimizationalgorithm(NWCSO);Pare.
2016-06-21。
黄 强(1992—),男,硕士研究生,研究方向为人工智能算法在电力系统中的应用;
李锦焙(1989—),男,硕士研究生,主要研究方向为智能算法在电力系统中的应用;
孟安波(1971—),男,博士,副教授,研究方向为人工智能算法在电力系统中的应用;
王 朗(1988—),男,硕士研究生,主要研究方向为电力系统运行与控制;
陈思哲(1975—),男,副教授,博士,研究方向为可变频率变压器的变速变频近海风电系统控制的应用。
国家自然科学基金项目(51307025)。
Project Supported by the National Natural Science Foundation of China(51377162).
1674-3814(2017)04-0011-08
TM734
A
