考虑实际工程环境中含可中断负荷备用优化模型研究
2017-06-27杨昆王浩夏能弘
杨昆,王浩,夏能弘
(上海电力学院,上海 200090)
考虑实际工程环境中含可中断负荷备用优化模型研究
杨昆,王浩,夏能弘
(上海电力学院,上海 200090)
针对电力系统实际运行中对备用辅助服务影响的3种不确定因素进行分析,首先利用场景分析,使用场景生成的方法进行传统下的备用市场优化建模,然后提出一种发电备用和可中断负荷备用综合考虑的系统效用最大模型。算例验证了该模型能有效地应对系统发生的对备用服务影响的3种不确定性因素,在系统的效用最大化前提下,实现发电商和可中断负荷提供的备用的优化配置,对实际工程环境下的备用市场调度具有指导意义。
备用服务市场;场景分析;效用差异;备用市场调度
随着电力系统的不断发展,用户作为需求侧的一部分,能够通过调整用电行为参与到电网运行中来,在保障系统安全稳定运行的同时也给自身带来了一定的经济收益。可中断负荷(Interruptible Load,IL)作为需求侧管理的重要组成部分[1],作为需求侧备用容量资源,在目前全球能源紧张,环境污染严重的情况下,可中断负荷在参与电力系统运行时需先与电网公司签订合同,其内容主要包括负荷中断量、中断次数、中断时间、补偿费用、提前通知中断时间等。一般来说,可中断负荷主要面向大于一定容量的大用户,需要连续中断一定时间,短时间内中断次数不宜过多,低于最大中断次数,除此以外,提前通知时间作为影响用户损失的重要因素也是其参与系统运行的一个重要指标。在调度过程中,可中断负荷出力与火电机组相比,可中断负荷成本无需开机费用更加经济,不受爬坡速度约束,出力更加灵活,可视为虚拟发电厂中的机组备用以代替火电发电机组备用容量,但其可中断次数,可中断量限制了其参与系统运行,这就需要对其进行优化调度。可中断负荷参与系统运行既提高了系统的发电容量,保证了整个系统备用容量的充裕性,同时有利于减少备用成本和污染物的排放量。
在电力系统实际运行中,可中断负荷参与备用辅助服务市场容易受到实际运行产生的三种不确定因素的影响:机组故障引起的备用,机组在电力生产过程由于意外而发生失去生产能力,这就需要有一台机组在其运行时时刻准备能够及时替代它,即为实际运行机组设置的备用。负荷变化引起的备用,电力负荷需求预测由于是日前完成的,所以可能存在一定的误差,另外某些突发的情况让负荷出现随机的波动情况。这就需要设置一定的备用来满足负荷出现的巨大波动,保证系统能够安全稳定地运行。输电元件故障引起的备用。输电元件由于意外发生故障导致功率传输受阻,使得其部分容量无效。此时电能量或者备用就要重新分布。以上3种因素对电力系统实际运行中备用辅助服务的影响程度是不一样的。
目前已有些文献提出了多种可中断负荷参与下的市场备用优化模型,文献[2]提出了以网损最小为目标函数建立了在负荷高峰期可中断负荷参与下的电力市场备用优化调度。文献[3]提出了从电网公司角度出发,以其调度备用容量利益最大为目标函数,发电机组和可中断负荷参与下的备用优化调度模型。文献[4]提出了以深化调峰费用,可中断负荷费及网损费用之和为目标函数,一种可中断负荷参与的计及大容量机组深化调峰的调度优化模型。文献[5]提出了计及发电机组和可中断负荷参与的两者效用的优化模型。
这些文献在目标函数上、约束上、交易算法和优化繁简程度上都有所不同,但是研究目标基本都是一致的,即在考虑不同约束的情况下以购买不同种类的备用成本最小为优化目标,这些文献未能考虑电力系统实际情况下发生的不确定性因素,或是在发电商和可中断负荷备用参与的情况下,仅考虑两者之间的购买成本差异,未能反应两者之间的计及环境,政策等各方面的效用差异。
本文在前人研究的基础上利用场景分析的方法,针对电力系统运行中发生的对辅助服务影响的三种不确定性因素进行分析,先利用场景分析的方法进行传统备用市场下的备用优化建模,接着综合考虑发电商和可中断负荷提供的计及环境,政策等各方面的效用差异进行优化建模,最终实现两者提供备用资源的优化配置。
1 场景分析概述
1.1 场景集的生成
场景分析法是一种能够解决随机不确定性问题的有效方法,通过将实际中可能出现的影响问题的不确定性因素进行场景化,进而转变成多个确定性的场景问题,从而降低建模和求解的难度。
场景分析是模拟电力系统运行状态的一种重要方法,利用场景分析的方法能够分析电力系统实际运行过程中突发的运行状态[6~8]。不同的电力系统对预想场景的分类可能不同,为了便于模型表达,引入预想场景集的概念,预想场景集由不同的单一场景构成的,表示电力系统复杂场景集。一个预想场景集包括3个子集,分别是负荷变化子集(将间隙性再生能源发电作为负荷处理)、机组故障子集、线路故障子集。电力系统在研究时段内的一个可能运行状态称为一个场景s,系统所有可能出现的场景构成的集合成为场景集S。
在经典的场景集算法中,将相邻的两个场景片段形成一个场景集采用的方法叫作笛卡尔融合。即一个规模为X的场景片段和规模为Y的场景片段作笛卡尔积形成一个规模为XxY的场景集片段,并且能够保证概率的归一性。
基于以上电力系统运行中发生的对辅助服务影响的3种不确定性因素,将电力系统中的负荷正常情况设为场景片段x1,机组正常状态设为场景片段x2.输电线路正常状态设为场景片段x3。
场景集可设为S={x1,x2,x3},其中出现场景片段x1的概率为p(x1),出现场景片段x2的概率为p(x2),出现场景片段x3的概率为P(x3)。
通过这样划分到整个调度区间T上,考虑实际工程中要满足N-1原则,故整个调度区间场景集的划分就为6种场景,分别为x1x2x3;x1x2x3;x1x2x3;x1x2x3;x1x2x3;x1x2x3,对应为S1,S2,S3,S4,S5,S6。通过生成场景集可对电力系统运行中的不确定因素进行模拟。根据3个场景片段的概率,作笛卡尔积融合得到如下用6种场景:
场景1:负荷正常,机组正常,线路正常。

场景2:负荷变化,机组正常,线路正常。

场景3:负荷正常,机组故障,线路正常。
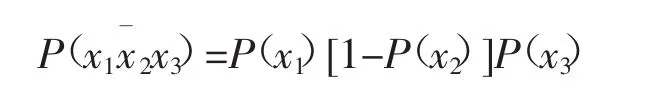
场景4:负荷正常,机组正常,线路故障。
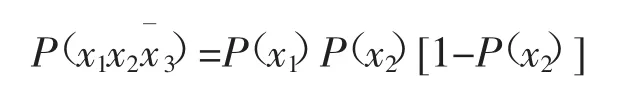
场景5:负荷变化,机组故障,线路正常。
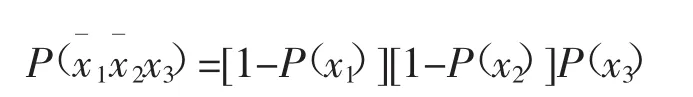
场景6:负荷变化,机组正常,线路故障。
这个场景是彼此独立发生的。
1.2 场景片段概率的求解
设负荷正常情况为场景片段x1,定义负荷正常为实际负荷与预测负荷的误差为4%,超过该值则认为负荷异常。如何计算P(x1)。
采用的方法是对采用某个地区的预测负荷和实际负荷作为样本[9~10],设一地区以1小时为间隔 24点间的负荷历史数据分别为a1,a2,a3,…,a24,预测负荷历史数据为b1,b2,b3,…,b24。然后计算每个样本的负荷预测误差值Δ1,Δ2,Δ3,…,Δ24。

计算每个样本的概率值。然后绘制负荷预测概率分布图。如图1所示。
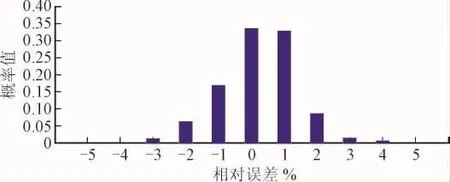
图1 绘制负荷预测概率分布Fig.1 Mapping load forecast probability distribution
计算相对误差在4%及以上的负荷预测概率之和,得到P(x2)。
设机组故障状态设为场景片段x2,机组故障率则为P(x2)。如何计算机组故障率。发电机组发生故障,降低了系统的备用容量和系统的可靠性。许多模型用一个常数来简化机组故障率,在实际运行中故障率并不是一个常数,而是受多种因素影响不断变化的。本文利用基于机组浴盆曲线的失效模式提出机组故障率模型[11]。
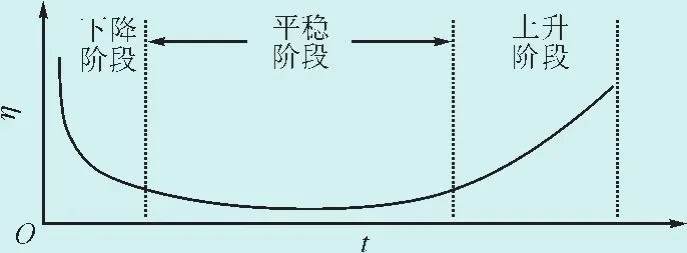
图2 机组浴盆曲线失效模型Fig.2 Fault model of unit bath curve
大型发电机组属于复杂设备,描述其故障规律的故障率曲线呈明显的3个阶段,即早期故障期、偶然故障期(又称为稳定运行期)和耗损失效期。基于失效模型考虑机组实际故障率水平采用新投运或检修完毕后投运机组的故障率。
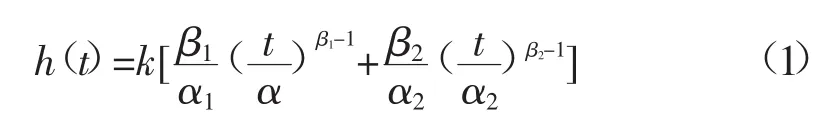
其中k为控制偶然故障期故障率;α1,β1为控制初始投运期故障率;α2,β2为控制老化期故障率。根据发电机组投运的时间计算出发电机组故障率则为P(x2)。假设不考虑线路故障的动态情况,考虑线路稳定状态,线路故障就可看作是线路断路故障这种情况。
输电线路故障状态设为场景片段x3,输电线路故障率为P(x3)。
比例故障率模型提出是一种综合考虑设备老化天气因素和设备状态的新型输电线路故障率模型[12~14]。输电线路内部的运行状况和外部环境条件通过该模型中的协变量来反映。
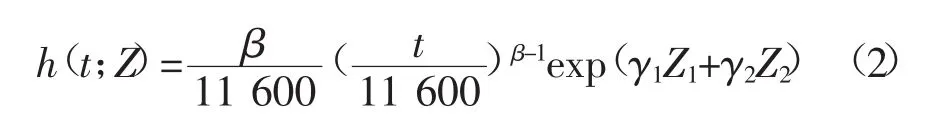
式中:β为形状参数;t为运行时间;γ1,γ2为相关协变量的谐系数,Z1,Z2分别为表示天气状态和设备状态值。根据这一模型计算得出输电线路的故障率P(x3)。
2 考虑可中断负荷的备用优化调度
2.1 传统备用优化的目标函数
多种场景下不确定问题转变为单一场景下的确定性问题,并为后期利用效用函数优化做准备。电力系统中期望成本最小可以作为运行人员选择最优调度方案的决策依据[15]。
先利用场景分析的方法进行传统备用市场下的备用优化建模,接着综合考虑发电商和可中断负荷进行优化建模,最终实现两者提供备用资源的优化配置[16~17]。
假设所有发电机进行投标,出于简化模型的考虑,未考虑发电机的启停成本。
第一步:函数的目标为各场景下的发电机的发电成本和购买备用成本之和的期望值最小。

m为总的预想场景数,将m个场景进行编号,k= 1,k=2,…,k=m;P(k)就是第k个场景所对应出现的概率;fGi为发电机成本函数;gRi为购买备用负荷的成本函数;为场景k下机组i在时段t的出力值;为场景k下备用负荷j在t时段的出力值为场景k下在t时间段机组的启停状态;场景k下在t时间段备用负荷的启停状态,为0-1变量,机组运行为1,停运为0,负荷中断为1,不中断为0。
2.2 传统备用优化模型的约束条件
(1)功率平衡约束
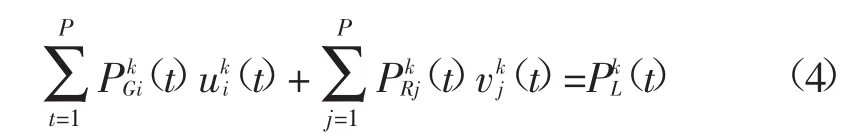
(2)机组出力约束
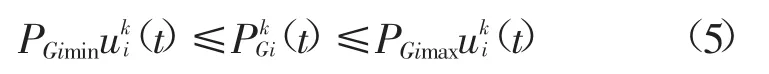
PGimin、PGimax分别为机组i的出力上下限。
(3)机组的爬坡约束

式中rdi、rui分别为机组i的上下行爬坡速率;Δt为调度的时间间隔。
(4)机组最小开机时间约束
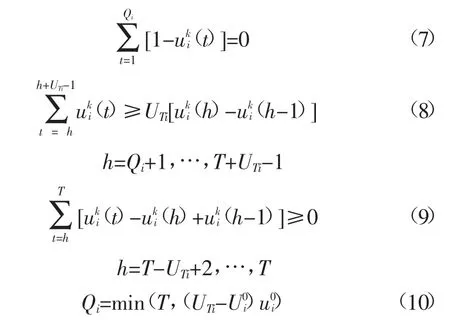
式中:UTi为机组i的最小开机时间;Qi为机组在初始时刻必须连续开机的时间;为机组i在初始时刻累计已
(5)机组最小停机时间约束
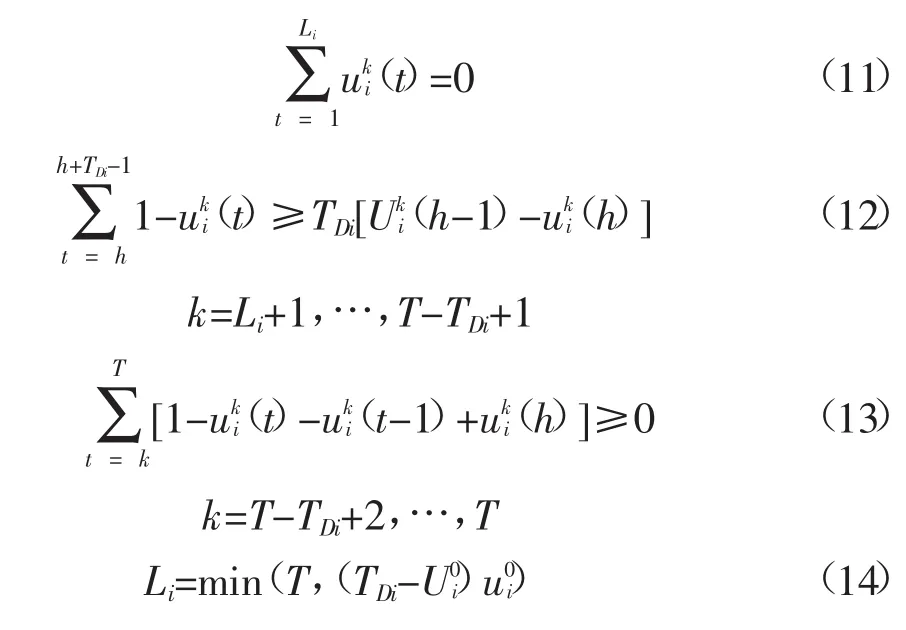
式中:TDi为机组i的最小关机时间;Li为机组在初始时刻必须继续停机的时间。
2.3 可中断负荷和发电备用的优化配置模型
假设可中断负荷和发电商提交分段的备用投标,将两种备用投标分别按照报价从低到高排序形成报价曲线,当市场主体和报价分段数目足够多时,可以将报价曲线进行平滑处理得到近似一次的备用供给曲线[18~22]。
由于两者备用在价格上有差异,但是两种备用又有一定的替代性,所以当系统购买备用总成本固定时,两种备用的配置有多种组合。系统购买备用容量的消费行为及其均衡状态可用如图3所示。
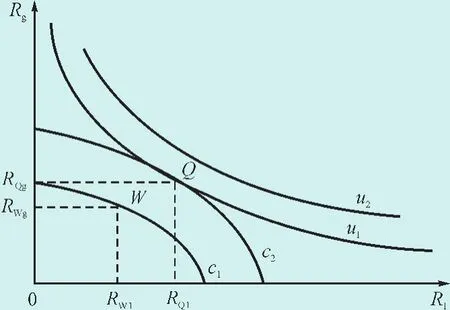
图3 系统购买成本和备用容量的无差异曲线Fig.3 The indifference curve system of purchase cost and spare capacity
依据无差异分析理论,选用柯布道格拉斯效用函数,能够反映系统购买成本与备用容量的无差异曲线凸向远点的典型规律,其中发电机备用或可中断负荷作为两种资源,任何一种资源越稀缺,其相对替代价值越大,相对于另外一种充裕的资源来说,其边际效用越大。随着发电机备用容量的增大,可中断负荷替代价值越大,边际效用增大。
消费可能曲线与无差异曲线相切时,在图中点Q反映最大化效用。点Q对应的发电机备用可中断负备用为最大效用的最优组合。
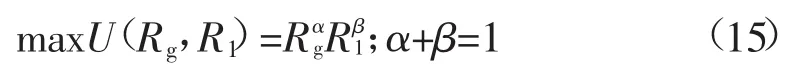
式中:Rg,R1分别为发电备用容量和可中断负荷备用;α,β为效用指数。α,β分别为和R1对系统总效用的相对重要性。根据α+β与1的大小分为3种情况,由于效率并不会随着Rg规模的扩大而提高,只有提高技术水平,才会提高效益。所以我们选取的是α+β=1这种情况。
为了方便求解,对两边取ln得到:
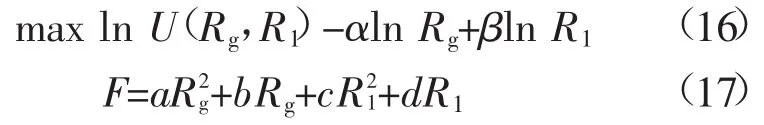
对于上述非线性约束,我们利用构造拉格朗日函数进行求解。
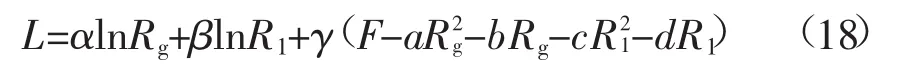
对Rg、R1、γ分别求偏导得到:

当模型各参数确定后,求得上述方程组的解。最终得到的是不同效用指数下,如何合理分配发电备用和可中断负荷备用的容量。整个模型求解流程图如图4所示。
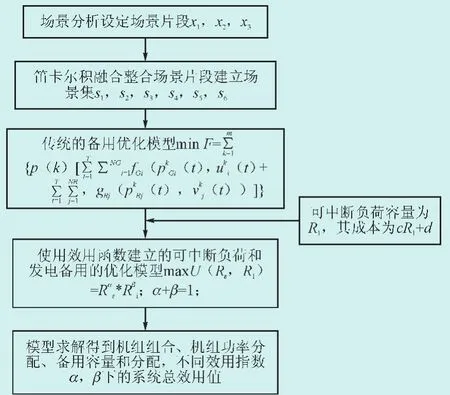
图4 模型求解基本流程Fig.4 The basic process of model solving
3 算例仿真
本文以 IEEE30节点系统对模型进行试验并验证如图5所示。
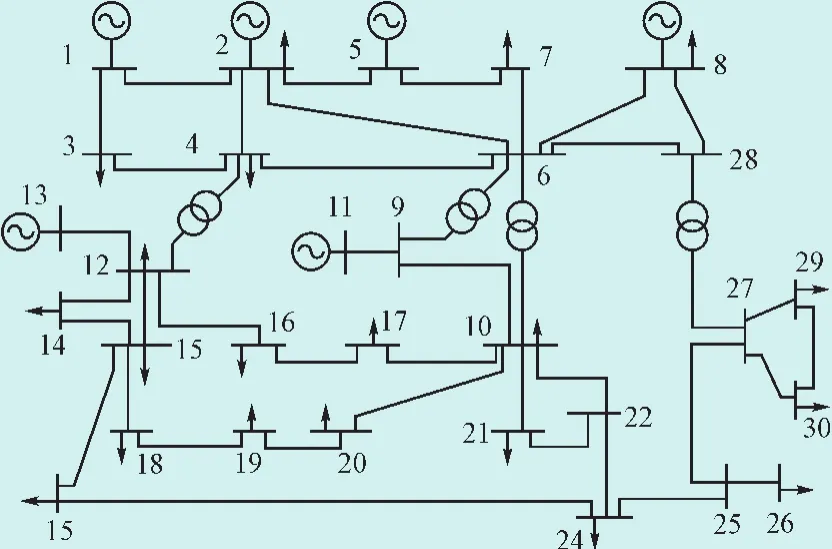
图5 IEEE30节点系统Fig.5 IEEE30 Node system
机组故障设定为13号机组故障,线路故障设定为支路6-8故障。该系统负荷需求见表1、可中断负荷市场报价数据见表2,发电机数据见附录A。
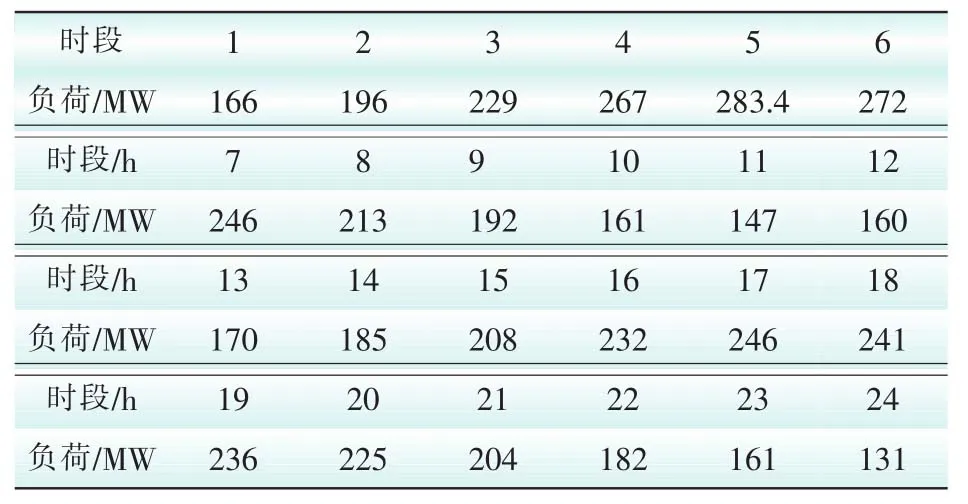
表1 系统负荷需求数据Tab.1 Load demand data of the system
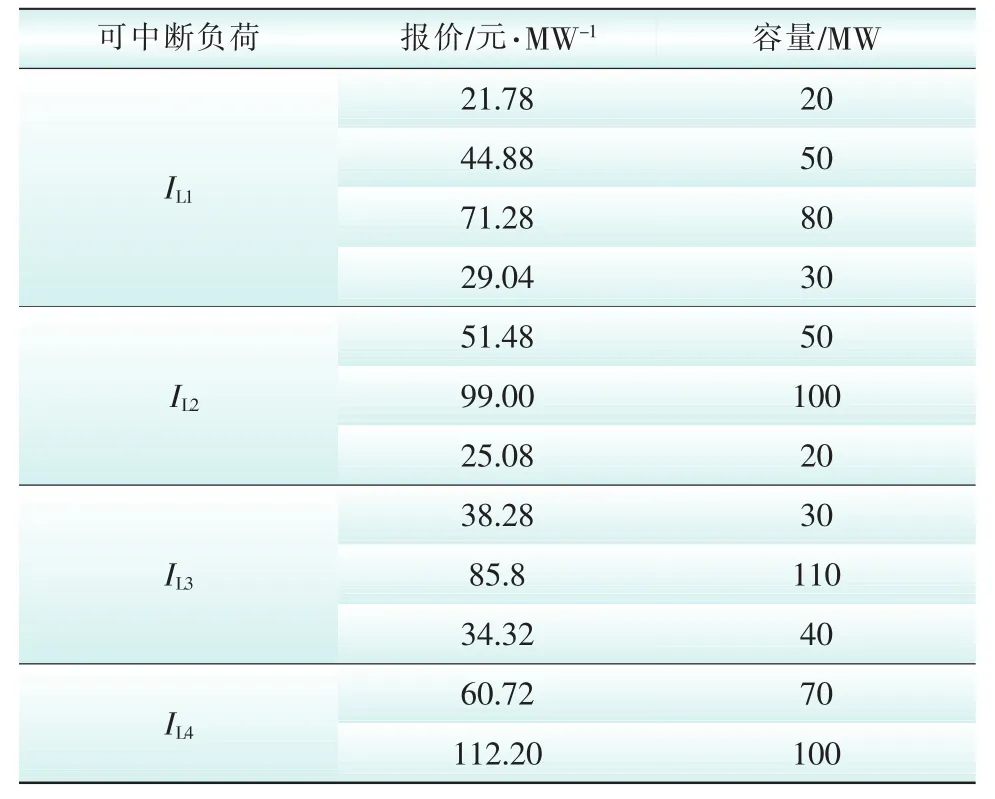
表2 可中断负荷市场报价数据Tab.2 Interruptible load market quotation data
根据图1负荷预测概率分布和式(1)~式(2),分析计算得到:
场景1:P(s1)=(1-3.8%)×(1-4%)×(1-8.2%)= 0.847 8
其余场景计算结果如下表3所示。
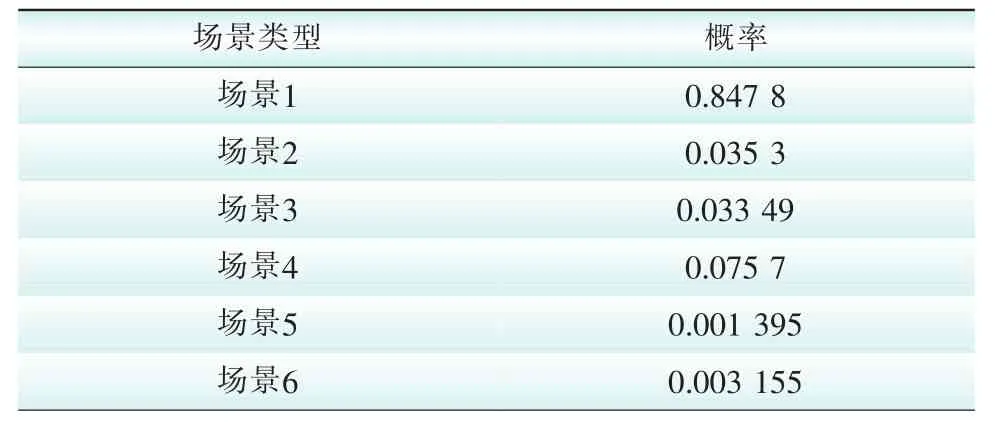
表3 复杂工程场景概率/&场景类型Tab.3 The scenario probability and/or scenario type of the complex engineering
将表3代入传统备用优化模型目标函数得到备用优化结果:期望总备用容量:66.73 MW期望购买备用容量费用:23 268.036元。
考虑实际工程中要满足N-1原则,故整个调度区间场景集的划分就为6种场景,分别对6种情况下1天24小时内机组旋转备用的容量和24小时内机组出力情况进行结果分析,如图6、图7所示。

图6 场景1:1天24小时内机组旋转备用的容量Fig.6 scene 1:The unit rotating spare capacity within 1 day 24 hours
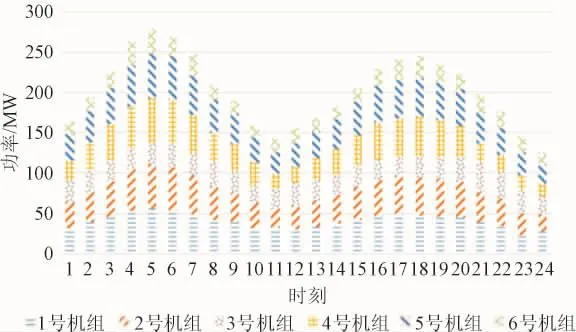
图7 场景1:1天24小时内机组出力情况Fig.7 scene1:Theunitoutputsituationwith1day24hours
分析图6~7可得作为场景1,系统正常状态下,机组5和6主要作为备用机组,留取备用容量较大,承载负荷较小。系统负荷主要由机组1、2、3、4承担。如图7-图11所示,将各场景对应一天内旋转备用容量和机组出力情况相比,一天24小时内机组旋转备用容量和机组出力情况相比,机组旋转备用呈现的曲线较为平滑,机组出力情况曲线随着负荷的波动呈现双峰的波动。这表明负荷对机组旋转备用的影响较小,而机组出力情况随着负荷的波动呈双峰波动。
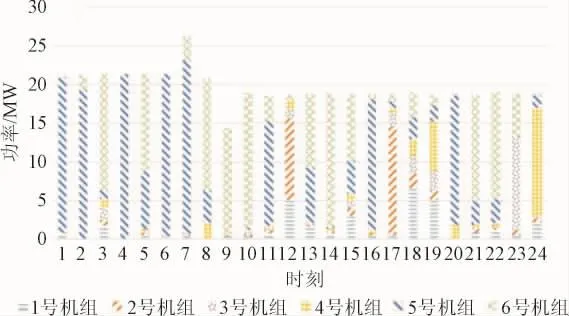
图8 场景2:1天24小时内机组旋转备用的容量Fig.8 scene 2:The unit rotating spare capacity within 1 day 24 hours

图9 场景2:1天24小时内机组出力情况Fig.9 scene 2:The unit output situation with 1 day 24 hours
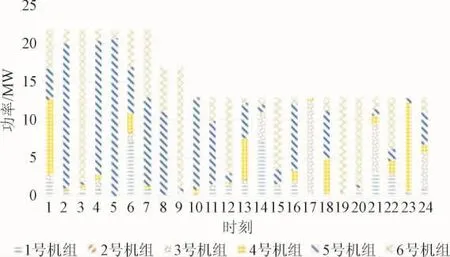
图10 场景3:1天24小时内机组旋转备用的容量Fig.10 scene 3:The unit rotating spare capacity within 1 day 24 hours
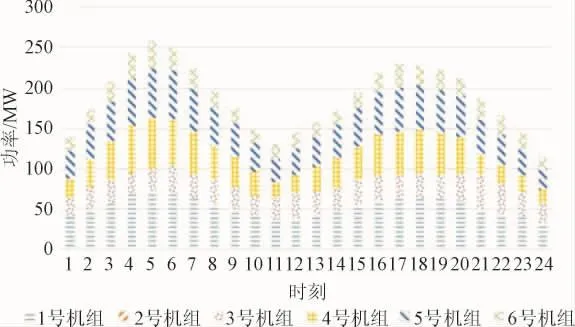
图11 场景3:1天24小时内机组出力情况Fig.11 scene 3:The unit output situation with 1 day 24 hours
由表4分析得到:负荷变化、机组故障、线路故障是影响系统总旋转备用容量及其费用的3个影响因素,但三者对其影响程度不一。将场景2、场景3、场景4的总旋转备用容量及其费用分别与场景 1的总旋转备用容量及其费用对照发现,负荷变化对于影响系统总旋转备用容量及成本的变化最为敏感,其次是机组故障,最为不敏感的因素为线路故障。以上3种因素任何一种发生都会提高系统的总旋转备用及其成本。使用效用函数计算结果如下表5所示。

图12 场景4:1天24小时内机组旋转备用的容量Fig.12 scene 4:The unit rotating spare capacity within 1 day 24 hours
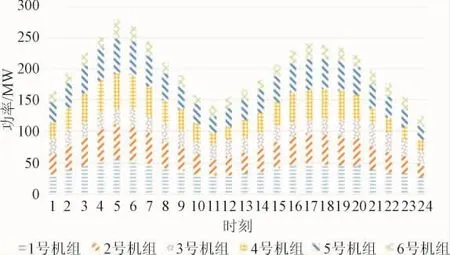
图13 场景4:1天24小时内机组出力情况Fig.13 scene 4:The unit output situation with 1 day 24 hours

图14 场景5:1天24小时内机组旋转备用的容量Fig.14 scene 5:The unit rotating spare capacity within 1 day 24 hours
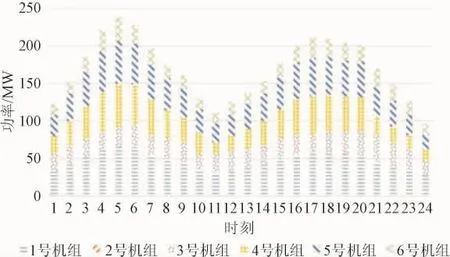
图15 场景5:1天24小时内机组出力情况Fig.15 scene5:The unit output situation with 1 day 24 hours
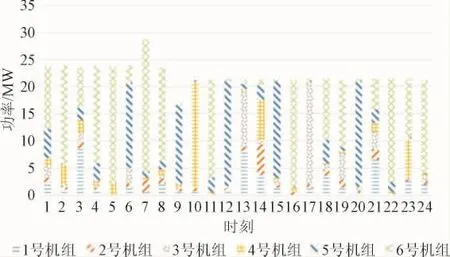
图16 场景6:1天24小时内机组旋转备用的容量Fig.16 scene 6:The unit rotating spare capacity within 1 day 24 hours

图17 场景6:1天24小时内机组出力情况Fig.17 scene 6:The unit output situation with 1 day 24 Hours
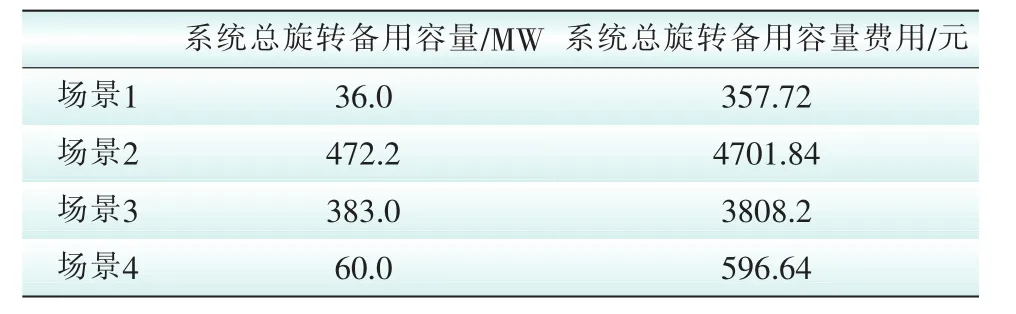
表4 不同场景系统总旋转备用容量及费用Tab.4 The total system spinning reserve capapcity and cost under a different scenario
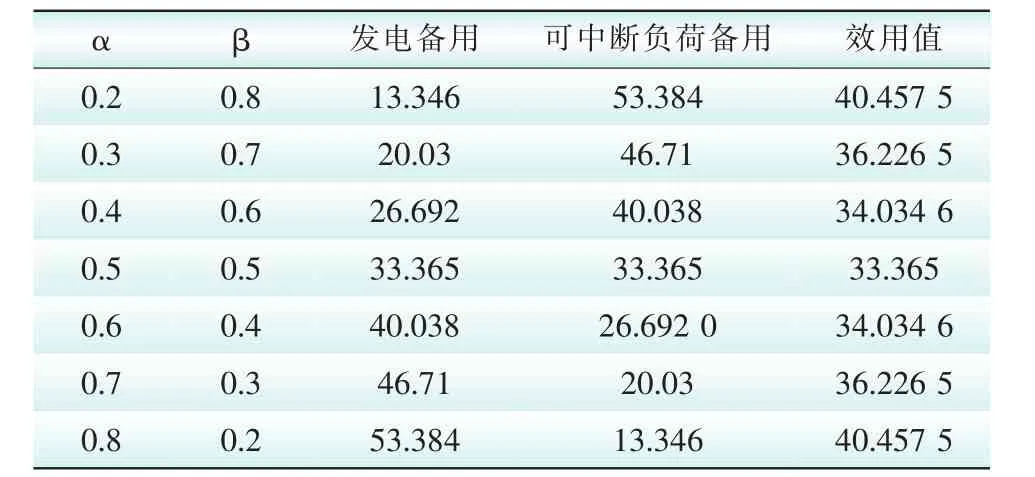
表5 不同效用指数下两类备用的优化配置结果Tab.5 The optimal allocation results of two kinds of reserve under different utility index
算例结果分析:
在发电商提供备用和可中断负荷总购买成本不变时,实现发电商提供的备用和可中断负荷对于电网可靠性提高等方面的效用差异优化。发电商提供的备用和可中断负荷对于系统整体的重要性大小反应在效用指数的差异上。当两者备用的效用指数相等时,系统总的效用值最低,两者的替代价值相同,边际效用一样,电网可靠性优化方面不是最优。当两者效用指数不一样时,系统总效用值随着两者效用指数的差值增加而增加。两者的效用指数越高的一方,其替代价值越小,边际效用越小对于系统的总备用的贡献越大。两者对于系统整体重要性差异体现在效用指数的不同,在实际工程中效用指数的差异反应在系统优化考虑因素的不同,例如电网公司角度的考虑购买备用的成本和可中断负荷的报价和容量大小、相应时间等因素;用户角度的考虑停电损失和获得赔偿等因素;社会效益最大化角度的考虑单位能耗和污染物排放量等因素。所以不同角度出发,系统优化考虑因素不一样,对应的两者效用指数是不一样的,即两者对于系统整体的重要性不同,则相应地选择不同的调度方案。
4 结语
对电力系统运行中不确定因素进行模拟,生成了不同类型的场景集,先建立了复杂场景下的备用优化模型,该模型求解机组组合、机组功率分配、备用容量和分配,然后通过建立可中断负荷参与下的备用优化模型,有利于增加需求侧弹性,缓解发电机备用不足引起的可靠性降低具有重要作用。该模型的备用优化结果较传统备用优化方法更为合理,不仅能够考虑可中断负荷和发电商备用成本的差异,还能够体现两者的效用差异,实现在系统总效用最大化前提下,发电商和可中断负荷提供备用的优化配置。
[1]张钦,王锡凡,王建学,等.电力市场下需求响应研究综述[J].电力系统自动化,2008,32(3):97-106.ZHANG Qin,WANG Xifan,WANG Jianxue,et al.Survey of demand response research in deregulated electricity markets markets[J].Automation of Electric Systems,2008,32(3):97-106(in Chinese).
[2]于娜芙,蓉薇.电力市场高峰时段可中断负荷优化购买模型[J].电力系统及其自动化学报,2010,22(4):89-93.YU Nafu,RONG Wei.Optimization model of interruptible load dispatch during the peak load time periods in the earlier power market[J].Proceedings of the CSU EPSA,2010,22(4):89-93(in Chinese).
[3]李晓军,谭忠富,王绵斌,等.考虑用户参与下电网公司购买备用的优化模型 [J].电力系统及其自动化学报,2007,19(2):9-14.LI Xiaojun,TAN Zhongfu,WANG Mianbin,et al.Optimal model of buying reserve capacity of power grid considering consumer’s participation[J].Proceedings of the CSU EPSA,2007,19(2):9-14.
[4]刘新东,陈焕远,姚程.计及大容量燃煤机组深度调峰和可中断负荷的风电场优化调度模型[J].电力自动化设备,2012,32(2):95-98.LIU Xindong,CHEN Huanyuan,YAO Cheng.Economic dispatch considering deep peak-regulation and interruptible loads for power system incorporated with wind farms[J].Electric Power Automation Equipment,2012,32(2):95-98(in Chinese).
[5]葛炬,张粒子.可中断负荷参与的备用市场帕累托优化模型[J].电力系统自动化,2006,30(9):34-37.GE Ju,ZHANG Lizi.Interruptible load participating in Pareto optimal model of reserve market[J].Automation of Electric Power System,2006,30(9):34-37(in Chinese).
[6]艾欣,周树鹏,赵阅群.基于场景分析的含可中断负荷的优化调度模型研究[J].中国电机工程学报,2014,34:25-31.AI Xin,ZHOU Shupeng,ZHAO Yuequn.Research on optimal dispatch model considering interruptible loads based on scenario analysis[J].Proceedings of the CSEE,2014,34:25-31(in Chinese).
[7]向萌,张紫凡,焦茜茜.多场景概率机组组合在含风电系统中的备用协调优化[J].电网与清洁能源,2012,28(5):61-69.XIANG Meng,ZHANG Zifan,JIAO Qianqian.Period coordination optimization of multi-scene probability unit combination in wind power system[J].Power Grid and Clean Energy,2012,28(5):61-69(in Chinese).
[8]刘俊杰,李树林,范浩杰,等.情景分析法应用于能源需求与碳排放预测[J].节能技术,2012,(01):70-75.LIU Junjie,LI Shulin,FAN Haojie,et al.Application of scenario analysis to energy demand and carbon emission prediction[J].Energy Conservation Technology,2012,(01):70-75(in Chinese).
[9]杨文佳,康重庆,夏清,等.基于预测误差分布特性统计分析的概率性短期负荷预测[J].电力系统自动化,2006,30(19):47~52.YANG Wenjia,KANG Chongqing,XIA Qing,et al.Short term probabilistic load forecasting based on statistics of probability distribution of forecasting errors[J].Automation ofElectricPowerSystem,2006,30(19):47~52(inChinese).
[10]赵希人,李大为.电力系统负荷预报误差的概率密度函数建模[J].自动化学报,1993,19(5):562~568.ZHAO Xiren,LI Dawei,Probability density function modeling for power system load forecasting errors[J].Automatica Sinica,1993,19(5):562~568(in Chinese).
[11]彭子平,刘波,陈清江.输电线路故障率模型研究[J].电力科学与技术学报,2014,29(2):52-57.PENG Ziping,LIU Bo,CHEN Qingjiang.Failure rate model for transmission line[J].Journal of electric power science and technology,2014,29(2):52-57(in Chinese).
[12]冯长有,王锡凡,王文博.考虑机组故障的发电厂商检修规划策略[J].电国自动化设备,2009,27(10):98-111.FENG Changyou,WANG Xifan,WANG Wenbo.Generator maintenance planning strategy considering generator failure[J].Electric Power Automation Equipment,2009,29(10):98-111(in Chinese).
[13]冯长有,伦涛,贺静波,等.计及风险的发电厂商机组检修规划模型[J].陕西电力,2012,40(9):59-65.FENG Changyou,LUN Tao,HE Jingbo,et al.Evaluation planning model of power generation unit based on risk[J].Shaanxi Electric Power,2012,40(9):59-65(in Chinese).
[14]谭芙蓉,白同朔,江志斌.大型发电机组等效故障次数的分析与计算[J].电力系统自动化,2004,28(23):61-64.TAN Furong,BAI Tongshuo.JIANG Zhibin.A statistic analysis of early failure rates of largesize generating units [J].Automation of Electric Power System,2004,28(23):61-64(in Chinese).
[15]吴杰康,史美娟,陈国通,等.区域电力系统最优备用容量模型与算法[J].中国电机工程学报,2009,29(l):14-20.WU Jiekang,SHI Meijuan,CHEN Guotong.Immune genetic algorithms for modeling optimal reserve capacity of interconnected regional power systems[J].Proceedings of the CSEE,2009,29(l):14-20(in Chinese).
[16]张姣,康广伟,黄滢芳,等.适应大规模风电接入的电力系统旋转备用优化模型与求解[J].陕西电力,2014,42(4):15-18,28.ZHANG Jiao,KANG Guangwei,HUANG Yingfang,et al.Optimization model and solution of rotating reserve for power system adapted to large-scale wind power[J].Shaanxi Electric Power,2014,42(4):15-18,28(in Chinese).
[17]杨昆,李曼.电量和有功备用辅助服务联合优化模型和算法的研究[J].陕西电力,2016,44(4):54-59.YANG Kun,LI Man.Study on joint optimization model and algorithm of electricity and active standby service[J].Shaanxi Electric Power,2016,44(4):54-59(in Chinese).
[18]王建学,王锡凡,张显,等.电力市场和过渡期电力系统可中断负荷管理:(一)可中断负荷成本效益分析[J].电力自动化设备,2004,24(5):15-19.WANG Jianxue,WANG Xifan,ZHANG Xian,et al.Interruptible load management in power market and interin system[J].Electric Power Automation Equipment,2004,24(5):15-19(in Chinese).
[19]孔祥清,雷霞,刘斌,等.节能减排背景下可中断负荷参与系统备用的优化模型[J].电网与清洁能源,2012,28(1):35-39.KONG Xiangqing,LEI Xia,LIU Bin,et al.Optimization model of intermittent load participation system in energy saving and emission reduction[J].Power Grid and Clean Energy,2012,28(1)35-39(in Chinese).
[20]武水英,肖长春,张虹.基于需求侧管理的可中断负荷实施的探讨[J].陕西电力,2008,36(10):43-45.WU Shuiying,XIAO Changchun,ZHANG Hong.Study on implementation of interruptible load based on demand side management[J].Shaanxi Electric Power,2008,36(10):43-45(in Chinese).
[21]尚金成,黄永晧,夏清,等.电力市场理论研究与应用[M].北京:中国电力出版社,2002.
[22]舒隽,李春晓,苏济,等.复杂预想场景下电力系统备用优化模型[J].中国电机工程学报,2014,32:105-110.SHU Jun,LI Chunxiao,SU Ji,et al.Optimal reserve dispatch model considering complicated contingency scenarios[J].Proceedings of the CSEE,2014,32:105-110(in Chinese).
(编辑 徐花荣)
附录A 基础数据
Research on Interruptible Load Standby Optimization Considering Actual Engineering Environment
YANG Kun,WANG Hao,XIA Nenghong
(Shanghai University of Electric Power,Shanghai 200090,China)
This paper analyzes the three uncertain factors that affect the standby service in the actual operation of the power system.First,the scenario analysis is used to build the backup market.Second,the paper proposes a kind of utility maximum model which considers power reserve and interruptible load reserve.An example is given to show that the proposed model can effectively deal with the three uncertain factorsthataffectthe standby service,and theoptimal allocation of the generator and interruptible load can be realized under the premise of maximizing the utility of the system.
standby service market;scenario analysis;utility difference;reserve market scheduling
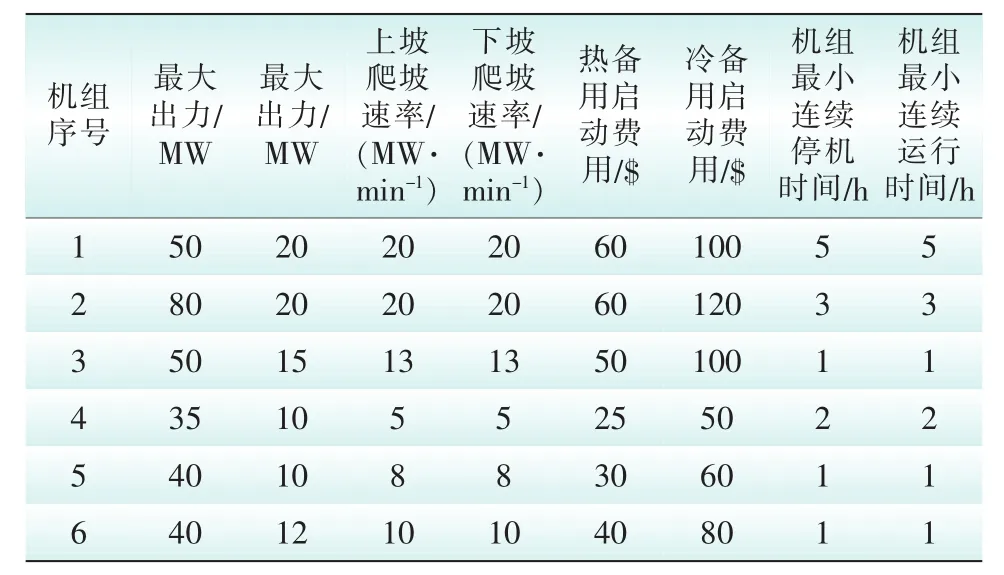
发电机数据(a)Generator data(a)
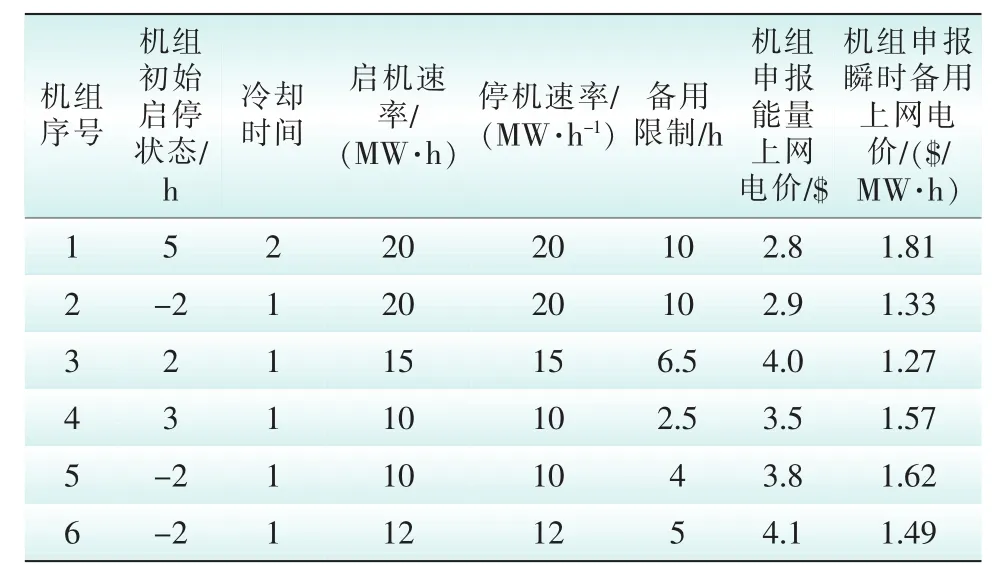
发电数据(b)Generator data(b)

2016-11-03。
杨 昆(1982—),女,博士,讲师,研究方向为电力经济与优化;
王 浩(1990—),男,硕士研究生,研究方向为电力经济与优化。
国家自然科学基金项目(51607110);上海市自然科学基金(14ZR1417600)。
Project Supported by the National Natural Science Foundation of China(51607110);the Natural Science Foundation of Shanghai Municipality(14ZR1417600).
1674-3814(2017)04-0048-09
TM744
A
