形式寻优:参数化辅助滨水空间形态规划设计

摘要：当前国内外景观设计行业中借鉴并引入了参数化设计技术，产生了丰富的景观设计形态。依托“形式寻优”理论模型，在滨水空间景观设计过程中，鉴别应用了新型参数化设计方法/技术。在滨水空间形态设计、形式生成环节上，创制了参数化辅助的寻优途径方法模型 （form finding model），并应用于实践规划与实验建造的设计项目。在实践过程中，该方法模型主动结合水文、水生态、水利学科及其相关工程技术，充分利用了动态开放系统的状态和自我调节力，同时具备了适应相似度较高的规划设计课题项目的能力，并为实际施工建造提供了经济、美观、实用的科学依据和理论基础。

关键词：滨水空间；设计研究；参数化；形式寻优；优化模型

中图分类号：TU986

文献标志码：A

文章编号：1671-2641（2017）02-0037-08

收稿日期：2017-04-01

修回日期：2017-04-26

Abstract： Nowadays， Parametric design as newly technique is introduced to landscape architecture design field all over the world， at the same time， various forms are produced. Based on the category of “form finding model”， the paper discusses the application and distribution of new parametric method in the design of waterfront space. The parametric assisted form finding model and method are being used not only in the design， but also the construction process. The further outcome of this model will be widely used in practical planning and structure projects. In the following practice process， the model actives adapt to water context， water ecology， water conservancy science and related technology， meanwhile，and takes fully advantages of the system dynamic and adaptability. The model would be used for related projects and contribute to the economy， aesthetic， and the utility of projects.

Key words： Waterfront Space；Design Research；Parametric design；Form Finding；Optimized Model

參数化设计由最初在建筑领域的发展应用并逐渐扩展到城市规划领域和景观设计领域，作为一种设计辅助方法：首先它是一种思维模式，一种方式的选择。再者，它是一种将数学逻辑、几何逻辑、算法逻辑等设计问题相关联，从自然科学的角度寻求解决问题的途径。Anderson J R在其学术文章中列举了景观建筑学中可以应用算法逻辑的例子，并视作一种利用创新思维来解决问题的方法[1]。而在造型领域，例如雕塑和构筑物的“人造表皮”，基于参数化计算结果产生不同的造型形式的算法逻辑已经有所普及[2]。在中国近年来参数化设计方法出现了异常繁荣复杂的局面，学术界中关注这一领域发展的学者逐渐对发展现状建立了认识基础，在技术应用方面，也出现了一些以“非线性参数化”为技术手段进行风景园林设计的探索。然而，如何正确甄别各种方法的优劣并有效地利用参数化手段成为当前需要关注的问题。

1参数化设计的案例鉴别

1.1目的单一的参数化设计

这一参数化方法最初出现在建筑立面设计环节中，其本质是通过编程方法，利用智能计算来代替重复性的人的体力劳动，进而发展出针对建筑构件，或者以重复韵律为审美追求的线性设计的辅助性形态程序，即针对其中某一单元素进行重复的参数化设计。例如构筑物的造型、铺装的形式、装置造型等。这种方法虽然独立但是局限性很大，仅适用于局部的细节设计，无法掌控尺度更大的场地，也无法进行具有复合目标的多样设计。

1.2自动生成式参数化设计

Peter Eisenman设计的犹太人大屠杀纪念碑群，通过参数化手段，设定规则和一组按照某种规律分布的高度值，借助软件平台自动生成设计，并形成多个相似的方案（图1）。

这种方法可以部分地弥补人脑机能在建筑或景观形态生成过程中造型能力不足的问题，但是由于真实的建筑或景观形态设计要受制于很多实际因素，因此参数化设计更多的是在暂时忽略一些因素的前提下，去生成可供参考的形态，离真实建造出来的形态，乃至真正能投入使用的形态还相去甚远。人的感知思维方式就像在开车教学中，专门练习入库、贴库、倒库等技术环节并形成了口诀，这种只利用规则而不去实际操练的方法，离真正的开车上路还很远。

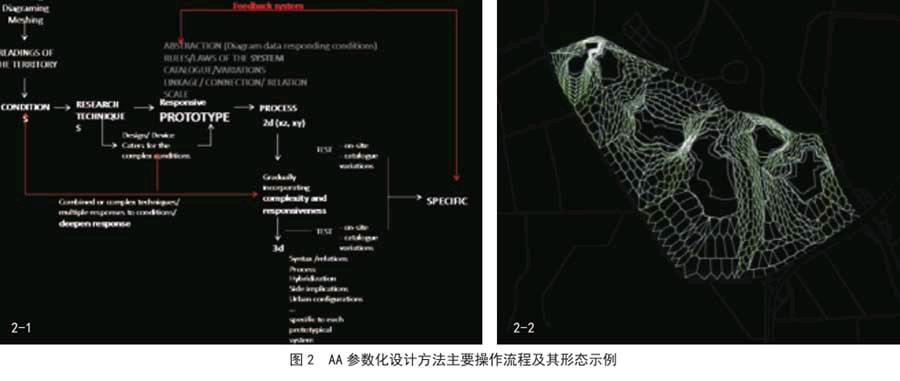
1.3英国建筑联盟（AA）景观都市主义参数化应用

AA的参数化设计方法相对以上两种更进一步，等高线成为他们最善于利用的参数，经过Indexing ，prototype，mesh，function等一系列过程再结合后期建筑师、景观师的主动选择来选择最优形式（图2）。但如果从实际建造工程应用角度而言，这是一种较为单线的思维方式，缺少优化和反馈设计，因此在实际进入施工设计阶段后，该方法会面临越来越多的因素群的影响。因此，后期的生成形式会出现一些锐角等不太符合人体舒适度的设计形式。

1.4鉴别结果

纵观以上三个案例，可以发现参数化设计在建筑设计领域和风景园林设计领域的发展总体上呈现出自上而下不断地进步，并不断完善的参数化设计方式，但依然存在一些需要完善的地方。本文试图通过对案例的鉴别总结，整理出一种具有一定适用范围的风景园林参数化设计模型，并在实际风景园林实际建造过程结合验证，期望得到一个相对优化的参数化设计的基本原型，并根据此原型总结出针对相关案例的普适性方法。

2郊野滨河空间参数化设计模型的建立

本文选取风景园林中的郊野滨河空间类型和参数化结合为基础案例，有以下考虑：1）可供考虑的因素群体类别较为丰富，便于验证参数化设计方法的多样联合，趋于接近真实的园林环境；2）参数化设计编程应用中可借助数学方法（例如：线性回归方程模块和模糊数学模块），对因素之间的影响建立分析和反馈（例如：层次分析方法），从而进行科学验证和选择[3-5]。

2.1参数化设计基本原型和框架建立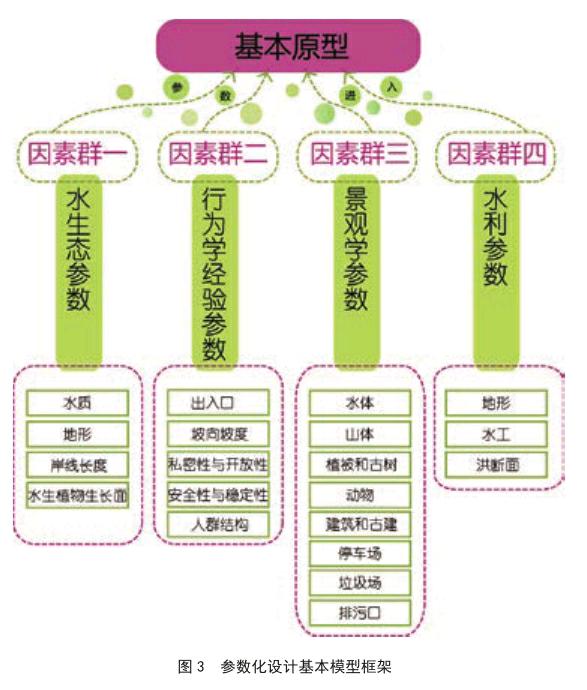

总体技术路线：针对滨水空间场地的特殊性，因地制宜选择有针对性的因素群，分析筛选因素群内部的重要参数，用数学模型模拟出真实反映场地特征的参数，并将各个参数进行量化，带入相应的程序中运算，得到相应的结果。通过各个参数的运算结果叠加，并加上设计师主观优化判断，形成初步的设计形式[6]。

2.2因素群及其相关参数的选择

2.2.1水生态参数

由于参数化辅助设计是技术操作法则，因此主要是应用相关学科的结论性观点作为支撑。例如：根据一般景观生态学观点，认为在水陆交错带生态群落中，岸线的长度和曲度越大，生物净化的能力则越强，生态性也越良好，那么这种关系可以量化构成参数化编程基本运算单元中的正线性代数关系。

另外如地表径流汇集而成的水体，其水质经过测评后可以确定区域内是否需要人工干预使其达到环保标准。由水利学专业（专业工种水工）计算给出是通过潜流湿地或是表流湿地的方式，并伴随有一定的有效水域面积要求的条件，这些都可以成为参数化设计数学模块的参数输入端。以此类推，关于水生植物生长面布局，地形的坡度、坡向等，均可以纳入等高线体系进行要素群的归类[4]。此步骤的最终目的是要建立要素群之间的数学联系（图3）。

2.2.2行为学经验参数

在确定建立要素群之间的数学联系后，便可对场地可达性进行研究探索，从而为设置下一步设计（如：合适的出入口、与场地紧密结合的路径）形态提供科学计算依据。在一般的行为学研究中，认为针对距离场地的远近不同，人们会选择不同的交通工具。例如是否在步行范围内，有无人行道、斑马线是影响人们选择步行出行的重要因素；相应的，自行车道及自行车停车位的有无，公交站点的有无，周边市政道路的级别及停车场的有无等，都将影响市内游客的可达性。城市对外交通枢纽则会影响外省市游客的可达性。这些行为学经验参数，为上一步得出的要素群之间的数学联系关系提供了参数调节的依据和可能性。如果把上一步比喻成一个发声的话筒，那么第二步便是话筒声音的音量调节键。

设计不可缺少的是满足不同的空间需求，空间的基本需求主要由三项因素（WWH）构成：WHO，WHEN，HOW。在更大的研究范畴内（即该场地所处的城市格局），通过调研，发现可以叠加更丰富更多元的参数（例如：针对当地人口结构、出行目的、娱乐方式进行研究），进而得出更多可能性和结论（在此案例中：市内游客的滨水空间需求度），这个方法成立的前提是研究对象的行为目的具有统一性（在此案例中：外省市游客多以旅游为出行目的，当地市民多以休闲娱乐为目的），从而得到优化设计的目的。

2.2.3景观学参数

在此案例中，针对滨水空间的研究，在景观学参数结合了《公园设计规范》《湿地公园设计规范》《郊野公园设计规范》等法规性文件中一些指标性质的参数规定，目的是为了检验参数化生成形态是否“合规”（例如常见的“硬质景观比”“落叶常绿比”等）。另外还可以通过收集相关的成功案例，进行比较研究，得出可供参考的数据 ，从而得到更为优化的數据，这一步骤作为参数化设计模块中的“检验端”，不可缺少，不但对之前设计步骤的正确性进行了检验，并进行了反馈设计（feedback design）。除此之外，根据更详细的园林数据，可以更好地与实际设计场地结合，从而达到“形式寻优”的基本目的。

设定任何现状资源的两个维度（积极+，消极-），其方法论近似于矩阵分析方法[7]（图4）。

本参数化模型建立在原场地的详细踏勘调研上，紧密结合园林景观建造过程涉及到的要素，并根据场地条件充分适应本案例情况。例如：

水体：水体的清洁情况，视觉感受，与水的互动、亲水空间；受污染的水体，视觉与嗅觉的双重因子（积极+，消极-）；山体：山地景观，台地景观，微地形，远山背景，相互关系为A-B（积极+，消极-）；

植被：空间围合，植物景观（积极+，消极-）；

动物：是否拥有良好的生态栖息地，是否能吸引游人（积极+，消极-）；

建筑：优美的建筑可以与景观相融相契；反之则会削弱好感度（积极+，消极-）；

古树：重点保护节点，人群集中区域，较好的观赏、教育、旅游资源（积极+，消极-）；

古建：重点保护节点，人群集中区域，较好的观赏、教育、旅游资源（积极+，消极-）；

停车场、垃圾场，排污口：视觉上不甚美观，气味也无法让人产生愉悦的感受（积极+，消极-）；

实际要素的设定和矩阵评价在数理原理上是层次分析法，在参数化编程模块中是产生要素与要素之间影响关系的数学子模型。

2.2.4反馈参数（在此案例中为主要水利参数）

在利用三维模型通过以上步骤对原场地经过一系列塑造设计之后，原场地发生了一定程度的改变。与此同时，此过程设计的基本形态（如地形、水系、植被等）必须输送给水利学的生态水专业工种进行进一步的各种计算。该工种根据变化后的地形重新建立洪水模型，进行复核计算，以检验景观设计提供的地形、水系、植被设计是否符合水利相关要求[8-9]。

需要说明的是，上述的参数设定，在内涵上更接近“影响要素”，具有灵活性，可以根据不同场地的不同调研结论，在计算过程中对参数进行设定。因此本文论述的重点在于算法和原理，打个比方相当于侧重重视数学方程式的建立，而X、Y、Z具体数值根据具体的场地来输入。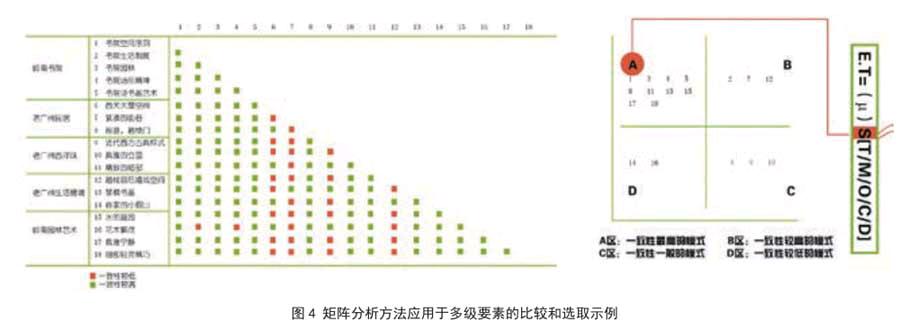

2.3参数的算法

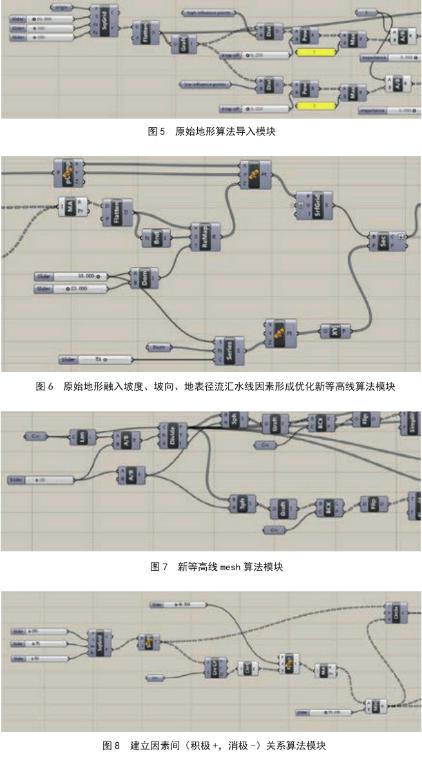
2.3.1地形算法（图5～7）

通常在原始地形CAD矢量文件导入Rhinocer和Grasshopper后，作为整个算法的基础，首先需要建立Indexing计算模块，为下一步引入上述相关生态、行为参数等调节端作准备。

由于原始地形矢量信息所包涵的坡度、坡向和地表径流汇水线等重要信息，可以在这个环节的算法上被分析释放出来，因此寻得虚拟最优理想地形模型。

这一步骤将上述成果推进一步，进入Meshing步骤，在算法中得出可供分析每一个地形细微单元的mesh面。以上图示算法模块的计算结果会在同步的可视化窗口形成图像，下文案例详解中演示。

2.3.2影响参数

设计中的单一要素对应一个参数，大多是单因素进行组合递进发展，而各因素之间并无明显联系。基于事物都是普遍联系的观点，多因素相关是一个良好的必然趋势，值得更深入地探讨。因此建立相关的算法模块也是文章下面所要建立的“形式寻优”模型的组成基础。

3基于参数化原型的寻优原型

寻优原型建立的流程是通过项目背景、文化、业主需求等分析定位，在基本原型（basic prototype）的基础上应用分析方法抽象出参数并利用参数化设计软件设定算法，通过调整参数的取值范围（range），得到一些量化指标，再结合景观学设计知识进行筛选比较，确定最优形式，关于此项目针对的参数如前所述。

3.1因素群的选优

各个参数之间具有相对独立性和潜在关联性，运用层次分析法对四个因素群内的参数进行过滤选优，列出纵横2个方向的规则矩阵表（表1，根据2.2得出），表明参数之间存在的内部和外部的逻辑关系。

表中A、B、C、D、E分别表示水生态参数、行为学经验参数、景观学参数、水利（反馈）参数。任意一个参数内部的逻辑关系以AA或BB等形式来表示，BA则表示B影响A生成。以此类推。在进行分析时，根据实际案例的特点来选取对角线上的某个选项作为起点，然后按照首尾相接的关系进行逻辑关系组合，例如AA-ACCB-BD-DA。组合表达的含义是生成的水生态参数影响景观学参数，以景观学参数为影响源生成行为学参数以此类推。从表中进行推算，根据此项目，可以得到4×4×4×4=256种可能的组合，提供了多种可能的技术路线，以便进行参数化设计。

3.2因素群内参数的过滤选优

同理，根据以上方法，因素群内的参数也运用规则矩阵法进行相互关联，选出因素群内部相对更重要的主导因素及相对次要的因素（表2）。

3.3寻优原型（form finding）的生成

针对场地特征，利用层次分析法对参数进行选优，将相对独立的参数关联起来，使优选出的主导参数更具科学性。以选出的参数为线索，由计算器设定算法，得到相应的结果。将一系列结果进行叠加，可得到初步的设计形式，这也是寻优原型的初始原型。这显然还不够完善，在最终的寻优原型确定之前，还需要设计师主观结合景观学的设计研究成果、典型景观模式的实践经验来进行寻优。对于参数化设计结果的提炼，需要借助设计研究成果，例如传统景观布局研究、水系分形学研究、师法自然的植物種植、景观肌理构成原理等。典型景观模式中如曲径通幽、一池三山、黄金分割等都能成为最终寻优原型的辅助因素，这也使多因子综合生成最终的寻优原型，附带上了传承文化的意义[9～10]。寻优原型生成过程示意如图9。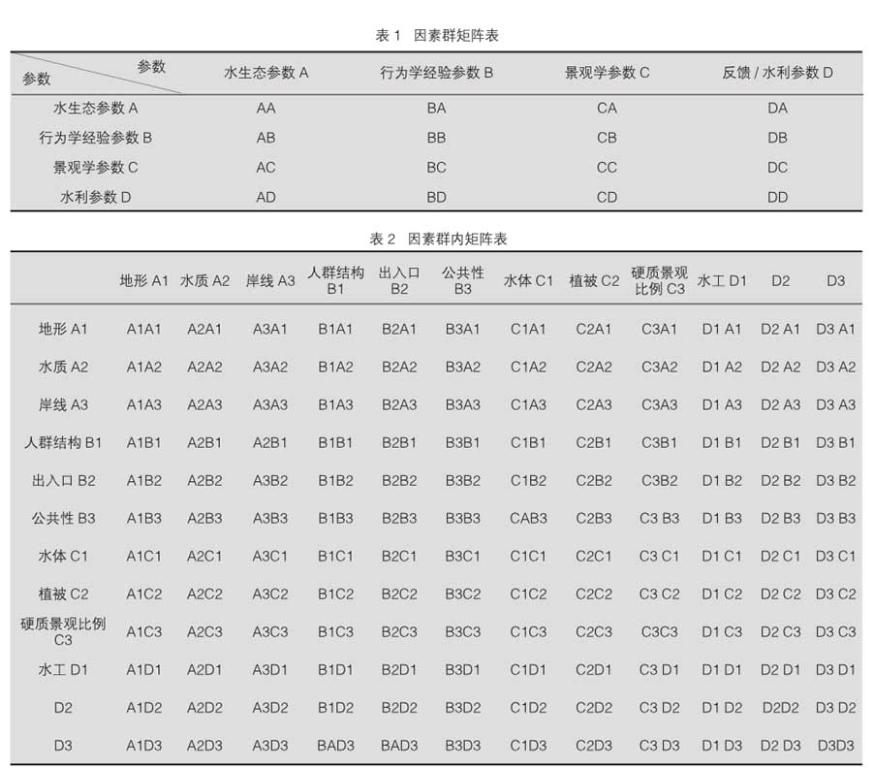

4案例详解

4.1项目简况

实践案例为山东省德州市徒骇河禹城段河道综合整治，禹城市地处山东西北部，历史悠久乃大禹之故乡，作为治水重地同时也是“龙山文化”发源地之一，作为本文的实际验证案例非常合适。

4.2挑战与目标（与文化内涵结合过程）

从历史文化保护利用角度看，禹城是历史上大禹治水的功成名就之地，而徒骇河作为链接城市和未来城市新名片大禹文化园的唯一生态廊道，具有重要的战略意义。如何引导和体现大禹精神以及地域文化特色是本案的重要挑战之一，也是可供设计工作者主管创作的来源之一，同时场地条件十分适合与参数化相结合。

而从园林景观工程建造角度看，该营建如能通过原始的、本土的材料选择，以一种宏大叙事的方式展示人类久远的生产、生活经验，从而为当代人提供一个可供瞻仰和体验的诗意的景观格局，应该是合乎该地域特色的选择。另外，从久负盛名的大禹治水神话传说中挖掘内涵，聚合谈天说地，疏导人流集散，顺应自然之势，是继承大禹治水“因势利导”的本质特征，本实践案例将“因势利导”理念融于场地相关生态设计与园路设计，作为本设计的精神文化支持。针对游憩人群数量确定园路和空间节点的集散、大小等，通过系统科学的承载分析，推演出最终的游憩路线和空间雏形关系。

4.3基本原型（basic prototype）的建立

4.3.1因素群及其相关参数的选择（表3）

4.3.2参数的算法

1）地形

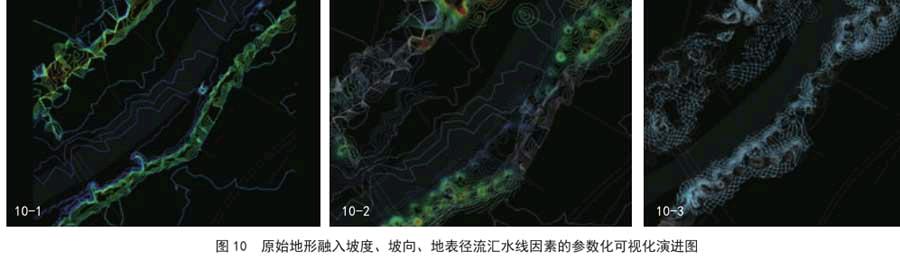
将原场地的等高线进行汇水线分析，可以发现一些水流汇集的区域和水流分散的区域，前者为场地的潜在低洼地，后者则为场地的潜在高地。利用这些潜在低洼地和潜在高地，生成了新的模拟等高线。这些新等高线只是模拟了原场地地形变化的一种可能与放大，同时也将场地的实际情况进行了科学化的整理（图10）。

等高线（contour）只能表明横向的结构，因此将不均一的四边形嵌套进新等高线内，生成一张mesh网格（mesh grid），这样在横向和纵向两个方向上都可以体现出一定的结构，形成了可以控制的单元（unit）。而这个四边形网格的选定，则主要由设计对象的尺度决定（图10）。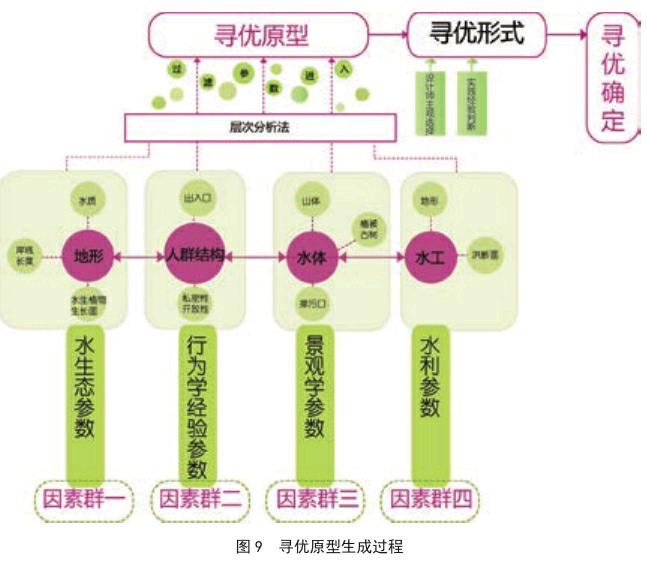

2）选址与尺度—湿地

由于现有的污水处理厂会将一定的污水量排入徒骇河内，为了对此进行整治，需要有一定的潜流湿地区域。

经过水工计算，处理污水量需要的潜流湿地面积总共为4 hm2，而潜流湿地处理必须细分为若干单元，每个单元的面积至多为1 500 m2，潜流湿地处理单位长度则应控制在12～30 m内，最小面积则约为150 m2。

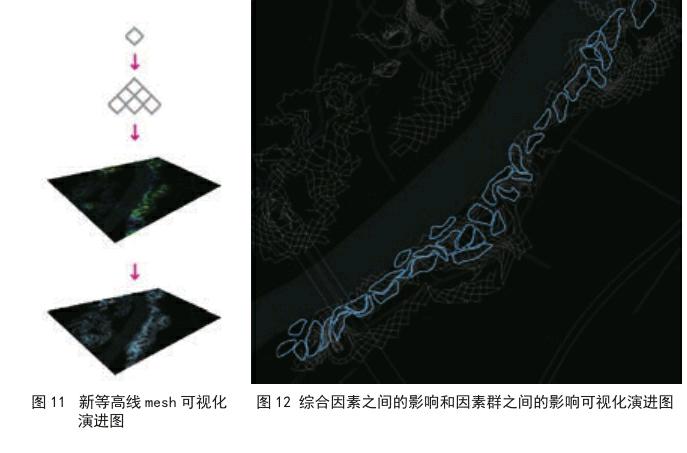
Mesh网格中的每个四边形都有一定的面积，可以帮助遵循湿地的面积要求。选择在相对低洼的场地内框选出湿地单元（unit），最终组合形成湿地的设计雏形（图11）。

3）选址与尺度—广场空间与道路选线

经过生态与城市的基础设施比较和功能分析，可以得出一些适宜做入口广场的区域。

运用禹城人口结构百分比及禹城地区出行目的人口百分比，与一定的生态系数进行数学计算，可以得出徒骇河的人口承载量。再根据与城市交通的分析可以得出各滨河入口空间将预计承接的人口承载量。通过这样科学的假设与计算，可以在场地内设计足够人们活动的空间且与徒骇河的生态相平衡。

在入口广场汇集的人群，需要通过园路分散到河边路各节点（node）。依据广场的承载量可计算出需要园路需要分散的承载量。随着园路分枝渐多，园路承载量也相应减少，因此园路会呈现不同宽度的分级。通过园路与园区的广场与节点的组合交叉，最终形成完整的全园的道路系统（system）。以之前计算得出的广场与道路的尺度为基础，再依据适宜坡度、适宜坡向、适宜建设用地等生态分析结果进行选线。

4.4形式寻优

应用层次分析法筛选的主要参数进行运算，得到可能的设计形式，设计师主观上结合实践经验，选出最终的最优方案（图12）。

5结语

对参数化寻优原型（form fi nding）的探讨，不仅是在追求一种科学的计算方式，更意在增加科学对设计过程的介入。将因素群中的参数进行数学量化，不仅增加设计的科学性，更促使了学科间的交叉对话。寻优途径的目标不仅在辅助主观选择，平衡了土方量，更增加了景观的美观、经济、实用性。最重要的是，为实际施工建造提供了充足的科学依据。

注：本文图1来自百度图片；图2为笔者2012年参与的AA—清华景观助教工作课件；图4来自参考文献[7]；图3、图5～12为笔者自绘。

参考文献：

[1] Anderson J R， Ortega D H. Innovations in Landscape Architecture [M]. Routledge， 2016.

[2]Xichang W， Sheng L. The Landscape Sculpture Design and Manufacturing Research Based on Parametric Design

and 3D Printing[C] New York：Smart City and Systems Engineering （ICSCSE）， International Conference on. IEEE， 2016：94-96.

[3]吳俊勤，何梅.城市滨水空间规划模式探析[J]. 城市规划， 1998 （2）：46-49.

[4]李敏，李建伟. 近年来国内城市滨水空间研究进展[J].云南地理环境研究，2006，18（2）：86-90.

[5]张鎏. 现代城市纪念性广场景观设计[D].长沙：湖南大学，2009.

[6]Roudsari M S， Pak M， Smith A. Ladybug： a parametric environmental plugin for grasshopper to help designers create an environmentally-conscious design[C]. France： Proceedings of the 13th International IBPSA Conference Held in Lyon， France Aug， 2013.

[7] 梁尚宇.回应生活—景观设计中事件记忆转置设计方法探讨[C].北京：中国风景园林学会2010年会论文集（上册），2010.

[8]廖文根，杜强，谭红武，等.水生态修复技术应用现状及发展趋势[J].中国水利，2006（17）： 61-63.

[9]宋晓猛，张建云，占车生，等.水文模型参数敏感性分析方法评述[J].水利水电科技进展，2015：35（6）：105-112.[10]Seeger C J. The role of facilitated volunteered geographic information in the landscape planning and site design process[J].New York： GeoJournal， 2008：72（3-4）：199-213.

[11]唐登银.黄秉维院士开创自然地理研究新方向[J].地理科学进展，2013，32（7）：1024-1026.