基于TVP—VAR模型的有色金属价格时变相关性研究
2017-06-27吴丹胡振华
吴丹+胡振华


摘 要:基于TVP-VAR模型,考量有色金属价格时变相关性。结果显示,铜价、铝价及锌价之间存在显著的正向相关关系;一种有色金属价格发生变化,其他两种有色金属的价格通常出现正向响应,并且这种响应的强度是时变的。时点脉冲函数结果表明,不同时点下有色金属价格之间的相关关系是不同的,但大多时点下表现为正相关关系。
关键词: 有色金属价格;时变相关性;TVP-VAR模型
中图分类号:F830.93 文献标识码: A 文章编号:1003-7217(2017)03-0064-07
一、引 言
有色金属不仅是国民经济、工业和生活不可或缺的基础材料,还是重要的战略物资。随着中国工业化進程的迅速发展,对于有色金属的需求不断增加。近年来,有色金属价格波动剧烈,金属价格之间相互影响,关系越来越密切,有色金属价格之间的相关性研究正引起学者们的广泛关注。
Cuddinggton和Liang(2003)[1]研究了不同汇率制度下的有色金属等大宗商品的价格波动。Watkinshe 和McAleer(2006)[2]采用伦敦期货交易所的铝、铝合金、铜、铅、镍、锡和锌期货价格研究了有色金属市场的风险溢价和持有成本,研究发现现货市场、期货市场和利率市场存在显著的协整关系,铝和锌市场之间存在长期稳定的相关关系。Basoglu等(2014)[3]使用伦敦金属交易所中的有色金属进行因果检验,结果发现铝是其他有色金属的格兰杰原因。吴冲锋等(1997)[4] 分别研究了上海期货交易所和深圳期货交易所以及上交所和伦敦期货交易所的铜价格引导关系,结果发现上海与深圳的一月铜,上海的铜期货和现货之间存在即时的双向价格引导关系。陈建明和徐东贤(2007)[5] 利用含有误差修正项的因果关系模型,检验铜期货价格和铝期货价格间的引导关系,并发现铜期货价格和铝期货价格存在相互引导的关系。方兰和沈镭(2011)[6]采用VAR方法,对铝、铜、锌等金属价格波动研究,发现有色金属价格之间存在联动性,市场之间存在长期稳定的相关关系。周伟和何建敏(2011)[7] 通过Granger因果检验、GARCH模型以及广义脉冲响应函数等方法,对我国金属期货市场的交叉影响及其传导效应进行了实证研究。
从文献中可以看出,有色金属价格之间存在着紧密的联系,之前的学者对这些关系也进行了一定的研究。然而,有色金属之间的价格研究尚有不足,这些研究大多都采用较为基础的因果检验、VAR模型等进行检验,这些方法只考虑了价格之间的静态关系,对于研究价格之间的时变相关关系很少。研究价格的时变关系是一个比较复杂的问题,所以在传统的研究中很少涉及。Primiceri和Giorgio(2005)[8]在传统VAR模型的基础上,提出了带随机波动的时变参数向量自回归模型,即TVP-VAR模型。TVP-VAR模型能够很好地捕捉到经济结构的潜在时变特性,而Nakajima(2011)[9]采用马尔科夫链蒙特卡洛方法来估计带随机波动的TVP-VAR模型使得此模型开始大量应用于经济研究之中。随后一些学者的研究都表明TVP-VAR模型对研究非线性时变关系有着独特的优势[10-12]。
过去30多年中国经济发展迅速,且对外开放的程度也越来越高,于是国内有色金属的价格会受到国内外各种因素的影响。因此,中国有色金属价格之间的相关关系并不是固定不变的,它们之间存在非线性时变的相关关系。为此,本文采用带随机波动的时变参数结构向量自回归(TVP-VAR)模型来探讨铜、铝及锌价格之间的非线性时变关系,研究不同时间点价格之间的不同关系。
二、TVP-VAR模型
本文使用Nakajima于2011年[9]提出的带随机波动的TVP-VAR模型来研究有色金属价格之间的时变影响程度①。该模型的描述如下:首先,引入一个标准的结构VAR模型,定义式如下:
三、实证分析
(一)数据说明及描述
本文数据选用上海期货交易所的铜、铝和锌日度交易数据,考虑到锌从2007年3月26日才开始正式交易,故数据选取2007年3月26日至2015年6月30日的数据,经剔除非交易日和节假日,共获得2011个日度数据。数据来自于WIND数据库。
由于有色金属期货价格数量级较大,均值最小的铝价也达到了15564元/吨,为方便实证分析,故将原始数据取对数用以降低数量级。本文数据均采用原始数据取对数后的数据用做实证,用LN_X代表,数据的描述性统计分析见表1。
从表1可以看出,铜价的标准差最大,说明铜价格的波动是最大的。JB统计量显示,所有的价格序列在1%的显著水平下均拒绝服从正态分布的假设。时间序列的ADF单位根检验结果所示,价格序列均不平稳,但是对数后数据的一阶差分的平稳性检验结果显示,一阶差分的数据是平稳的。
(二)有色金属价格的相关性分析
为研究有色金属价格之间的关系,将三组价格序列放在一个图中进行考察,具体见图1。从图1 中可以看出,铜、铝和锌三者的走势比较接近,都于2009年初达到价格的最低点,并于2011年上半年重新上升到新高,随后出现比较稳定的走势。
进一步采用相关性检验检验其相关关系。选取Kendalls tau和Spearmans rho这两个相关系数来度量两个变量之间的变化趋势是否一致。两变量的各相关系数值见表2。
从表2可以看出,三种相关系数在1%的显著性水平下都显著异于零,说明有色金属价格之间都存在显著的正向相关关系。其中铝和铜价格的相关性最大,三种不同相关关系检验结果中最小的也达到了0.73,而剩余有色金属之间的相关关系最低也达到了0.48。
(三)TVP-VAR模型实证分析
TVP-VAR模型估计结果的主要评价标准有均值、标准差、95%的置信区间、收敛诊断值(CD)和无效因子。其中CD用于测定预测模拟得到的马尔科夫链是否收敛于后验分布,无效因子则是后验样本均值的方差和不相关序列样本均值的比率。相关参数滞后阶数的选取参考了Nakajima等(2011)的研究方法,这里对TVP-VAR模型选择了二阶参数滞后。从表3的估计结果可以看出,在5%的显著性水平下,模型没有拒绝参数收敛于后验分布的原假设,并且所有参数估计结果的无效因子都比较小,其中最大的无效因子为149.87,表明我们至少可以得到约132个(20000/149.87)不相关样本,这对于后验推断是足够的。因此,通过这些评价标准能判断模型的估计是有效的,可以进一步分析。
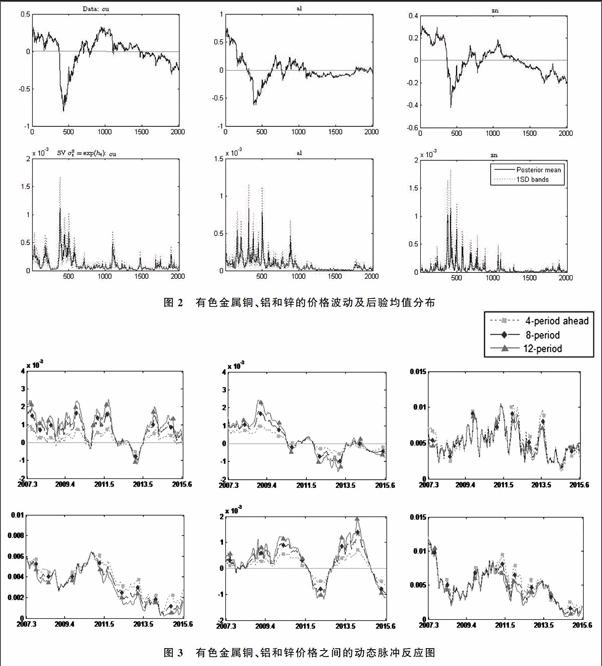
图2是铜、铝、锌的价格波动及后验均值分布图,其中左边两个子图为铜,中间两个子图为铝,右边两个子图为锌。图中所有子图的横坐标表示每一个时间所对应的数据点;图中第一行三个子图的纵坐标表示价格波动,第二行三个子图的纵坐标表示后验均值。从图中可以看出,采用带随机波动的TVP-VAR模型比较好地反映了各个变量的历史波动。各个有色金属价格在2008—2009年初出现剧烈波动,价格出现接近于直线型的下降。实际上,有色金属价格受2008年金融危机的影响,出现了大幅跳水,以铜为例,2008年2月25日的铜期货收盘价为69250元/吨,到2008年年末铜收盘价跌至25790元/吨,价格下降近2/3。随后中国政府通过出台一系列救市政策,才使得中国经济较早地走出危机并开始恢复,有色金属价格也开始回温,到2010年年初已恢复至60000元/吨左右。这些波动表明,随着宏观经济和政策的改变,有色金属价格出现时变性的波动。
从图3中可以看出,不同时间间隔的冲击响应函数走势基本上是一致的,表明模型估计具有稳健性。
(1)铜价格冲击,其他两种有色金属价格的脉冲响应。图3左边的两幅图分别代表铜1单位的冲击,锌和铝的响应。从中可以看出,对于铜的冲击,锌和铝都有较为剧烈的响应波动,且大多数时间都是正向的响应。具体而言,铜的冲击对于锌而言,先是出现了较为集中的正向响应,且在2010年达到最高,随后下降,并在2010年出现一点负向的响应,后又维持了近两年的正向响应,但在2013年又出现了较大的负向影响(2013年5月左右铜1单位的正向变动将导致锌价格下降0.001个单位),从2014年开始铜价格的冲击锌又出现了正向的响应,截至到目前仍然保持正向作用。而1单位铜价格的冲击,铝一直有正向的响应,并在2010年末至2011年初达到最高点,随后影响开始减弱,截至目前保持在较弱的正向响应。从两图中可以看出,对于铜价格冲击,铝有更为明显的响应,即铜对于铝的影响更大。
(2)铝价格冲击,其他两种有色金属价格的脉冲响应。图3中间两幅图分别代表1单位铝价格的冲击,铜和锌价格的响应。从图中可以看出,铝对于铜和锌的影响也比较剧烈,波动明显。其中,对于铝价格的冲击,铜价格在2011年前表现为正向的响应,但2011年后几乎都是负向的响应。而锌对于铝的冲击,则在2011年前表现为较为稳定的正向响应,而2011年后出现剧烈波动,具体表现为在2012年初出现负向低谷,而2013年下半年又出现正向高峰,随后又下降,目前仍处于负向的影响。
整体而言,有色金属价格之间大多出现的是正向的影响,而在2013年5月左右,锌对于铜和铝的冲击表现出负向的影响,铜对于铝的冲击也出现了负向的影响。而2011年前后各个变量的响应也有所变化。而2008年金融危机期间有色金属价格之间的影响程度有所弱化。2008年受世界金融危机的影响,金融市场持续震荡,投资者的投资避险意识增强,商品期货遭大量抛售,导致有色金属等大宗商品价格大幅跳水,而实证结果表明在危机时候,有色金属价格之间的相关关系有所减弱。经过2008年金融危机后,2009年世界經济开始复苏,有色金属等大宗商品需求上升,价格渐涨,等到2011年有色金属价格几乎已恢复到金融危机前的价格,但随着中国经济的发展出现短板,有色金属面临产能过剩、节能减排等影响,价格出现了剧烈波动,且出现价格下行,故2011年前后有色金属价格之间的影响程度都有所变化。
(3)锌价格冲击,其他两种有色金属价格的脉冲响应。图3右边的两幅图分别是锌1单位的冲击,铜和铝的响应。两幅图都可以看出,对于锌1单位的冲击,铜和铝都出现了正向的响应,且响应图围绕0.005波动,说明锌价格对于铜和铝价格都是正向的影响。两图均可看出,2008年金融危机期间对于锌价格的冲击,铜和铝的响应都有所减弱,而2011年5月铜和铝价格的对锌价格的响应达到峰值。其中,铜的响应幅度一直处于震荡中,且比较剧烈;而铝的响应则在2007年初的时候出现较为明显的下降趋势,锌的发行初期对于铝的影响达到了0.012左右,但是随后在2008年下降至0.0025,中间经过一段时间的较强影响,2013年5月后锌价格的冲击对于铝价格的影响开始减弱。综合两图来看,2011年前都有较大的正向响应,而2011年后,影响程度有所下降,但是相比于锌价格对铝价格的影响,锌价格对铜价格的影响更大。
综上所述,有色金属价格之间大多存在着正向的相互影响,但也有一些时点出现了负向的响应。在金属价格波动剧烈的金融危机时期,有色金属价格之间存在正向相关关系,但是相关关系有所减弱,而在经济恢复期和上涨期,有色金属价格之间的相关关系变得比较复杂。
2.时点脉冲响应函数的分析。从上面的时变脉冲响应函数可以看出,不同的经济周期期间有色金属价格之间的关系是有所不同的,故进一步对不同有色金属价格在不同时间点进行静态脉冲响应分析,用以分析有色金属价格之间的关系是否存在结构突变③。
选取四个用于对比的时点:(1)2007年5月1日(时点为150),代表有色金属价格波动较为平稳、锌步入正轨、中国经济快速发展的时点;(2)2008年7月11日(时点为311),代表有色金属价格迅速下跌、金融危机爆发的时点;(3)2011年3月26日(时点为1206),代表有色金属价格一路攀升出现新高点的时点;(4)2013年5月2日(时点为1484),代表有色金属价格平稳波动的时点。
图4左边两幅图分别为锌价格对来自铜价格的四个不同时期的正向冲击的静态响应以及铝价格对来自铜价格的四个不同时期的正向冲击的静态响应。从左上图可以看出,在初始期对于铜价格的冲击,锌都表现出了负向的响应,并在第一期达到最低点,随后上升,后面不同时期有不同的表现。具体而言,锌发行初始阶段和金融危机时期锌的响应在经历初期的负向响应后出现了正向的响应,并维持上升的正向趋势;而有色金属价格上涨和平稳时期,则一直维持在较弱的负向关系,这与前面的时变图是相近的。从图中可以看出,在锌发行初始阶段和金融危机时期,对于铜价格的冲击锌价格的响应程度更大,铜价格对于其影响更明显。左下图则表明,铜价格的1单位冲击对铝一直有着较为平稳的正向关系,其中在2007年有色金属价格处于高位时影响程度最大,其次为金融危机时期,影响最小的时期为2013年价格平稳时期。但是从图中也可以看出,不论是哪个时期,脉冲响应函数图都有向下的趋势,说明铜价格对于铝价格的冲击影响随着时间的推移有所下降。两幅图都表明,在2007年有色金属价格稳定和2008年金融危机时,铜价格的冲击对锌和铝价格有更大的影响。
图4中间两幅图分别为铜价格对来自铝价格的四个不同时期的正向冲击的静态响应以及锌价格对来自铝价格的四个不同时期的正向冲击的静态响应。中上图表明,不同时期铝价格的冲击铜价格有不同的响应,在2007年金融危机以前和2008年金融危机时,铜价格表现为向上的正向响应,说明铝价格对于铜价格有正向的影响,且两个时期的影响程度几乎一致;而有色金属价格上涨和平稳的2011年和2013年,铜价格对于锌价格的冲击表现出负向的响应,且价格上涨的2011年其负向关系更为明显。从中下图可以看出,铝价格1单位冲击,锌价格在2011年的有色金属价格上涨期间出现了负向的响应,但2007年有色金属价格平稳、2008年金融危机以及2013年有色金属价格平稳时期都出现的正向响应,其中2013年有色金属价格平稳时期影响最大。从上述两幅图都可以看出,铝价格对于铜价格和锌价格的影响都是逐渐上升的,并在2011年有色金属价格大涨时期都出现了负向的影响。
图4右边两幅图分别为铜价格对来自锌价格的四个不同时期的静态响应以及铝价格对来自锌价格的四个不同时期的静态响应。从右上图可以看出,铜价格对于锌价格有着正向的响应,且不同时期影响程度有所不同。具体而言,在锌开始交易的初期和金融危机时期,铜价格对于锌价格冲击的响应最小,初期锌1单位的冲击,铜价格变动0.0025单位。而在后面的2011年和2013年期间,锌价格对于铜价格的影响较初期有所上升,达到了0.01,后有所下降,并存在一定的下降趋势,两个时点影响幅度变化一致。右下图也表现出铝对于锌的正向响应,且不同时期的影响程度有所不同。金融危机时期锌价格的1单位冲击,铝价格对其响应程度最小,而2012年有色金属期货价格上涨时期,铝价格对于锌价格的响应程度最大,但下降趋势也最为明显。两幅图都表明,锌价格的1单位冲击,铜价格和铝价格都有正向的响应,说明锌价格对于其他两种有色金属都有着正向的影响,其中在锌发行初期和金融危机时期影响最小,而在期货价格上涨时期和平稳时期影响较大。
从图4可以看出,锌价格的冲击对于其他两者的影响最大,且两者都表现出了正向的响应;而对于铝价格的冲击,铜和锌的响应都较小。不同有色金属价格在不同的时点也表现出不同的影响。
四、结论及启示
以上时变脉冲函数结果说明,有色金属价格之间大多出现的是正向的影响,且这些影响波动比较剧烈,2008年金融危机期间有色金属价格之间的关系都有所减弱,而2011年则是有色金属价格关系变动的拐点。时点脉冲函数结果说明锌价格对铜和铝价格都有正向的影响,其中在锌发行初期和金融危机时期影响最小,而在期货价格上涨时期和平稳时期影响较大;铜价格在2007年有色金属价格稳定和2008年金融危机时对锌和铝价格有更大的影响;铝价格对于铜价格和锌价格的影響都是逐渐上升的,并在2011年有色金属价格大涨时期都出现了负向的影响。
综上所述,有色金属期货价格之间的关系主要是正向的相关关系。其中时变脉冲响应函数结果说明一种有色金属价格冲击,其他两种有色金属大多出现正向相应,并且随着时间的变化而不同,呈现出时变的特点;而时点脉冲函数结果则表明不同时点有色金属价格之间的关系不同,但大多表现为正向作用。以上研究结果对投资者和政府有一定的启示作用,对于投资者,在构建包含有色金属的投资组合时,应避免同时加入多种有色金属,以规避风险;另外,在分析不同有色金属价格相关性时,除了考虑全局的相关性外,更应该关注最新时点的相关性,以此来指导投资。对于政府,在目前有色金属价格较低的大背景下,政府应督促有关行业进行有色金属市场的去库存和供给侧改革。考虑到几种主要有色金属之间的紧密关系,政府可以通过调整某一有色金属的价格来影响其他有色金属的价格,达到以较少的工作来稳定有色金属市场价格的目的,将更多的精力放在有色金属市场去库存和供给侧改革上。
注释:
①TVP-VAR模型作为一种扩展的VAR模型,一方面,保留了VAR模型的优点,将系统中所有变量均视为内生变量,为解决变量之间的同时性问题、分离各变量对自身和其他变量冲击的动态反映提供了有用框架;另一方面,放松了模型系数矩阵和扰动项协方差矩阵非时变的约束,可以有效捕捉系统中的结构性变化以及变量之间的非线性关系,因而对于分析经济中各种时变特征具有明显的优越性。另外,Nakajima提出的带随机波动的TVP-VAR模型还可以捕捉到变量之间的潜在结构变动。因此,带随机波动的TVP-VAR模型比普通的VAR模型对分析三种有色金属价格的关系更合理。
②这里有很多方式来演化模型中的这些时变参数。根据Primiceri等(2005)和Nakajima等(2011)的处理方式。让at=a21,a31,a32,a41,…,ak,k-1′作为下三角矩阵At中的非0和1的元素,并且有ht=h1t,…,hkt′,hjt=log σ2jt,j=1,…,k,t=s+1,…,n。
③这种静态分析与传统的VAR模型脉冲响应近似,最大的区别在于其基于TVP-VAR模型,可以考虑不同时间点来进行静态脉冲响应分析,能对时变脉冲分析的结果进行一定验证和补充。
参考文献:
[1]Cuddington J T,Liang H.Commodity price volatility across exchange rate regimes[R].Georgetown University and IMF mimeograph.Working Paper 2003.
[2]Watkins C,Mcaleer M.Pricing of non-ferrous metals futures on the London Metal Exchange[J].Applied Financial Economics.2006,16(12): 853-880.
[3]Basoglu M S,Korkmaz T,Cevik E I.London metal exchange: causality relationship between the price series of non-ferrous metal contracts[J].International Journal of Economics and Financial Issues.2014,4(4): 726-734.
[4]吳冲锋,王海成,幸云.期铜价格引导关系和互谐关系实证研究[J].系统管理学报,1997,(2):1-9.
[5]陈建明,徐东贤.上海期货交易所期铜期铝价格关系的实证分析——运用误差修正模型检验Granger原因[J].有色金属工程,2007,59(3):112-114.
[6]方兰,沈镭.有色金属价格指数关联性的VAR分析[J].中国矿业,2011,20(1):36-39.
[7]周伟,何建敏.我国金属期货市场交叉影响及其传导效应实证[J].上海经济研究,2011(8):63-70.
[8]Primiceri G E.Time varying structural vector autoregressions and monetary policy[J].The Review of Economic Studies.2005,72(3): 821-852.
[9]Nakajima J.Time-Varying parameter VAR model with stochastic volatility: an overview of methodology and empirical applications[J].Jouchi Nakajima,2011,29:107-142.
[10]陈宗义.人民币汇率对中国长期贸易顺差的影响性分析——基于TVP-VAR模型的实证检验[J].统计与信息论坛,2012,27(2):62-66.
[11]胡利琴,彭红枫,李艳丽.中国外汇市场压力与货币政策——基于TVP-VAR模型的实证研究[J].国际金融研究,2014(7):87-96..
[12]刘林,孟烨,杨坤.结构变化、人民币汇率与我国股票价格——理论解释与实证研究[J].国际金融研究,2015(5):3-14.
(责任编辑:钟 瑶)
Abstract:This paper uses a time-varying coefficient vector autoregression model (TVP-VAR) to analyze the nonlinear dynamic relationship between the prices of the three major non-ferrous metals (copper,aluminum and zinc). Then it selects representative time point to analyze at different time points of the specific impact situation between non-ferrous metal prices.The empirical findings indicate that there was a significant positive correlation between the price of copper,aluminum and zinc prices.Changes in one of non-ferrous metals prices,the other two non-ferrous metal prices usually appears positive response,and the intensity of this response is time-varying.In addition,point impulse function results also show that at different time points the correlation between the price of non-ferrous metals are different,but in most cases points showed positive correlation.
Key words:Non-ferrous metals price;Time-varying correlation;TVP-VAR model
