气象参数对成都地区办公建筑能耗的影响及预测

侯立强++杨柳++李红莲++许馨尹++刘加平

摘要：

气象参数是影响建筑热环境和供暖空调能耗的主要因素之一。基于成都地区1971—2000年共30 a的历史观测数据，生成了建筑能耗模拟软件EnergyPlus所需要的逐时气象数据文件。比较分析了该地区30 a干球温度、太阳辐射等各气象参数月均值的变化，模拟分析了该地区建筑的采暖、制冷及总能耗，利用多元回归建立了建筑能耗与气象参数之间的关系式，并检验了该关系式的准确性。结果表明：成都地区办公建筑能耗变化与各气象参数没有呈现明显的规律性；建筑月总能耗与各气象参数呈纯二次多项式关系，月采暖能耗、月制冷能耗与各气象参数呈交叉二项式关系；建筑月能耗回归模型能够较准确地预测建筑月能耗与各气象参数的关系，且月采暖能耗和月制冷能耗回归模型预测的准确性优于月总能耗模型。

关键词：

气象参数；建筑能耗；能耗模拟；多元回归

Abstract：

Meteorological parameters is a major factor affecting building thermal environment and heating and air conditioning energy consumption， and climate change has a significant impact on building energy consumption. Based on 30 years historical observations of Chengdu from 1971 to 2000， the hourly meteorological data file is generated which is required by the building energy simulation software EnergyPlus. The changes of 30year monthly mean dry bulb temperature， monthly mean solar radiation in the area were compared and analyzed， and the heating， cooling and building total energy consumption is simulated and analyzed. At last the building energy relationship with meteorological parameters by using multiple regression is established， and the accuracy of the relationship is tested. The results shows that： the regularity relationship between change of building energy consumption and meteorological parameters isnt significant. the building monthly total energy consumption and meteorological parameters show a pure quadratic relationship， and a cross binomial relationship between monthly heating energy consumption， monthly cooling energy consumption and meteorological parameters is found. Building monthly energy regression model can predict the relationship between building monthly energy consumption and various meteorological parameters accurately， and the monthly heating energy consumption and monthly cooling energy consumption regression model predicts better than monthly total energy consumption model.

Keywords：

meteorological parameters； building energy consumption； energy simulation； multiple regression

建筑能耗在總能耗中所占比重较大，截止2013年，建筑能耗已超过总能耗的1/3[1]。影响建筑能耗的因素较多，包括室外气候、围护结构、室内环境及设备，其中，气象状况起着独特和重要的作用，直接影响建筑负荷及暖通空调能耗、照明能耗（受采光控制的建筑）和太阳能、风能系统的发电等。因此，研究气象参数对建筑能耗的影响具有重要意义。IPCC报告指出，建筑能耗对环境具有重大影响，气象状况与建筑能耗间存在显著关系[23]。目前，大多数研究采用室外平均干球温度或度日数来研究其对建筑能耗的影响[47]。Vipul等[8]采用干球温度分析法预测了建筑的年能耗。Mason等[9]利用澳大利亚78个地方的逐时气象数据建立了采暖能耗与采暖度日数的关系及制冷能耗与制冷设定温度的关系。Day[10]利用制冷度日数分析了澳大利亚珀斯的制冷能耗。Rosa等[11]考虑太阳辐射的影响，采用修正的度日数研究了采暖及制冷能耗。Dombayci等[12]采用度日数方法预测了土耳其代尼兹利的总能耗及耗煤量。这些方法虽然显示了建筑能耗与气象状况较好的关系，但绝大多数只是考虑单一要素，而建筑能耗受多个气象要素的综合影响。笔者采用多项式回归的方法综合分析了月均干球温度、干球较差、露点温度、风速和太阳辐射对建筑能耗的影响。

1气象参数与建筑能耗的关系

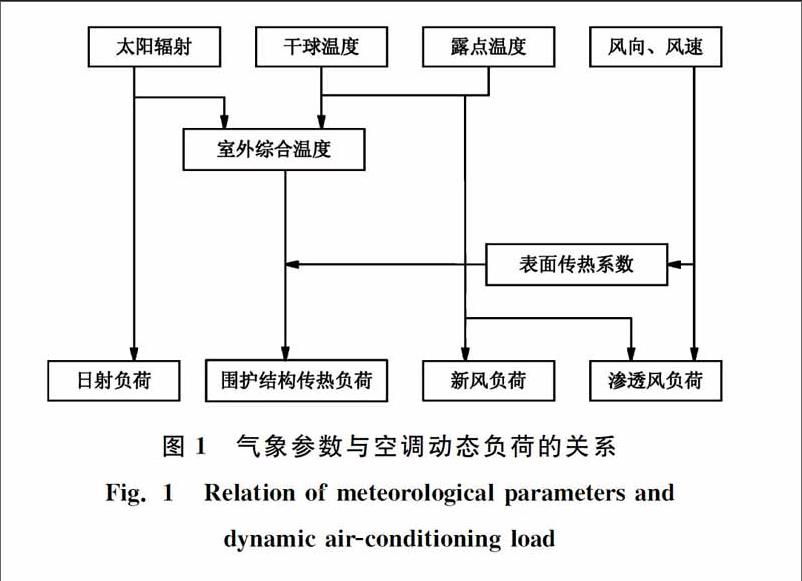
气象参数对空调及建筑能耗有重大影响，与建筑热环境分析直接相关的参数包括：干球温度、湿球温度、露点温度、相对湿度、太阳辐射强度、风速、风向。其中，湿球温度与露点温度相关性较强，可以选取其一作为主要分析对象。风向对建筑能耗的影响取决于建筑物的朝向。太阳辐射是最基本的要素，室外气温、湿度等都受到太阳辐射的影响，且产生围护结构的日射得热[13]。室外气温和湿度主要决定围护结构的传热以及新风负荷，也是影响建筑能耗的主要因素。干球较差（最大干球温度和最小干球温度差值）则体现了极端气候对能耗的影响。气象参数相互耦合，共同综合作用影响建筑负荷。笔者在研究气象参数对能耗的影响时，为了保证原有气象要素信息的完整性，没有选择单一气象要素，而是选取干球温度、干球较差、露点温度、风速和太阳辐射5项参数作为主要分析对象。图1为模拟软件中各气象参数与空调动态负荷间的关系。

2成都地区公共建筑建模

建筑能耗的动态模拟已成为建筑节能研究与实践的核心技术和重要工具，进行建筑能耗模拟分析，需要能耗模拟软件所需的气象数据文件。气象数据文件通常包含干球温度、大气压、露点温度、相对湿度、太阳辐射、风速、风向、云量等气象参数的逐时数据。首先利用中国气象数据共享服务网成都地区1971—2000年的太阳辐射日值数据及其他气象参数的4次定时数据生成了逐时数据，并转化为动态能耗模拟软件EnergyPlus所需的气象数据文件格式[14]，然后采用EnergyPlus软件进行建筑能耗模拟。

选取一典型空调办公建筑作为基准建筑，基准建筑为一栋20层的办公建筑，北轴夹角为0°。标准层为37.8 m×31.5 m平面，层高3.8 m，总建筑面积为23 814 m2，其中空调区域面积为21 609 m2，分布在建筑周围的4个区。建筑的基本概况如表1所示，内部负荷、室内设计工况及暖通空调系统设置如表2所示。

成都为夏热冬冷地区，既有夏季制冷的需求，又有冬季采暖的需要，且采暖和制冷能耗相当。气候变化时，采暖和制冷能耗均发生变化，为了探究气象参数对于全年能耗、夏季制冷能耗及冬季采暖能耗的关系，选取成都作为典型城市。以成都1971—2000年共30 a的气象数据为基础，并将其分为1971—1980年、1981—1990年和1991—2000年共3个不同阶段，研究分析了3个阶段干球温度、干球较差、露点温度、风速和太阳辐射的变化规律。成都地区1971—2000年月均干球温度、干球较差、露点温度、风速和太阳辐射变化规律如图2所示。

MBE反映了1981—1990年和1991—2000年各气象参数相对于1971—1980〖HJ1.8mm〗年的变化程度，MBE为正表示相对于1971—1980年偏大。一个月值的增大能够抵消另一个月的减小，因而引入了RMSE。RMSE反映了1981—1990年和1991—2000年各气象参数与1971—1980年的绝对差异。NMBE（normalied mean bias error）和CVRMSE（coefcient of variation of the root mean square error）则为对应的MBE和RMSE与1971—1980年各气象参数月均值的比值。成都各气象参数1981—1990年和1991—2000年相比于1971—1980年的比较分析如表3所示。

成都1971—2000年各气象参数变化规律不同。干球温度先减小后增大，整体增大；干球较差逐渐减小；露点温度逐渐增大；风速逐渐增大；辐射逐渐减小。成都1981—1990年干球温度、干球较差、露点温度、风速和辐射的NMBE分别为-1.29%、-3.5%、0.53%、23.89%和-13.19%，1991—2000年干球温度、干球较差、露点温度、风速和辐射的NMBE分别为2.47%、-5.12%、0.1%、28.90%和-17.69%，各气象参数变化量大小依次为风速、辐射、干球较差、干球温度和露点温度。

成都1971—2000年建筑总能耗逐渐增大，制冷能耗先减小后增大，整体减小；采暖能耗先增大后减小，整体增大。1981—1990年建筑总能耗增大是由于采暖能耗增大量大于制冷能耗减小量，1991—2000年建筑总能耗增大是由于制冷能耗的增大量大于采暖能耗的减小量。各气象参数变化均对采暖、制冷及总能耗有影响。制冷、采暖能耗变化与干球温度的变化相一致，干球温度减小，制冷能耗减小，采暖能耗增加；而与干球较差、露点温度、风速和太阳辐射变化不一致。各气象参数对建筑制冷、采暖和总能耗的影响程度不同，干球温度影响较大，其他气象参数影响较小，尤其风速、太阳辐射和干球较差变化量较大，但建筑制冷、采暖和总能耗变化不大。

3建筑能耗与气象参数的多元回归

研究一个因变量与一个或多个自变量间的多项式关系的回归分析方法，称为多项式回归（polynomial regression），自变量有多个时，称为多元多项式回归[15]。在多元回归分析中，如果因变量与自变量的关系为非线性的，但是又找不到适当的函数曲线拟合，则可以采用多元多项式回归。多项式回归的最大优点是可以通过增加自变量的高次项对实测点进行逼近，直至满意为止，可以处理相当一类非线性问题。任意函数都可以分段用多项式来逼近，因此，不论因变量与其他自变量关系如何，总可以用多项式回归来进行分析。

建筑能耗与5个气象参数呈非线性关系，可采用多项式回归分析的方法，这里采用较为简单的五元二次多项式来探究其关系。二次多项式回归方程一般分为4种模型：线性二次多项式、纯二次多项式、交叉二次多项式以及完全二次多项式，对应的建筑能耗与气象参数模型分别为

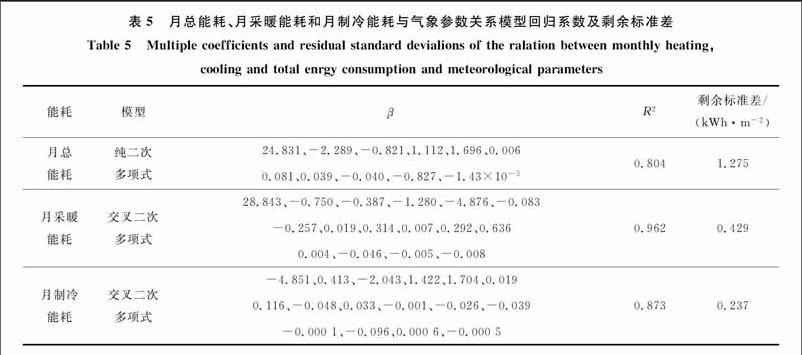
为了探究建筑能耗与气象参数的关系，建立并检验其关系式的准确性，利用成都地区1971—2000年气象数据进行了30次能耗模拟，从360个月能耗中随机选取340个，从1、2、12月共90个月采暖能耗中随机选取70个，从5、6、7、8月共120个月制冷能耗中随机选取100个来分别建立月总能耗、月采暖能耗及月制冷能耗与气象参数的回归模型。利用Matlab软件[16]进行五元二次多项式回归，分别建立月总能耗、月采暖能耗、月制冷能耗分别与月均干球温度、干球较差、露点温度、风速、太阳辐射的关系模型。理论上，完全二次多项式的精度最高，但其形式也最为复杂。在精度较高时，选用较为复杂的二次式形式时精度提高有限。因此，在达到一定精度（R2≥0.8）时选择形式较为简单的二次多项式形式。月总能耗、月采暖能耗和月制冷能耗與气象参数关系模型回归系数及剩余标准差如表5所示。

二次多项式能够较好地表现建筑月能耗与各气象参数的关系，其中月总能耗与气象参数近似呈纯二次多项式关系，而月采暖能耗和月制冷能耗与气象参数近似呈交叉二次多项式关系。月总能耗、采暖能耗及制冷能耗回归模型的R2分别为0804、0962和0.873，剩余标准差分别为1.275、0.429、0237 kWh/m2，表明成都月总能耗、月采暖能耗和月制冷能耗与各气象参数预测回归模型较为准确。

4模型评价

为了评估建筑能耗与气象参数关系模型的准确性，针对影响建筑能耗的5项气象参数进行了建筑能耗模拟。对成都办公建筑月总能耗、月采暖能耗和月制冷能耗分别选取了剩余20组进行了能耗模拟，并与建筑能耗回归模型的预测值进行了比较。模拟建筑能耗与回归模型预测能耗比较如图4所示。

成都地区办公建筑回归模型预测的月总能耗、月采暖能耗和月制冷能耗与模拟建筑能耗相比存在偏大和偏小，但总体两者较一致。图中的实线表示误差为0所对应的参考线。由图4可知，回归模型预测的月总能耗值绝大部分落在±13%的误差带以内，最大误差为-13.02%，平均误差为-4.06%；回归模型预测的月采暖能耗值绝大部分落在±10%的误差带以内，最大误差为-10.07%，平均误差为-1.27%；回归模型预测的月制冷能耗值绝大部分落在±5%的误差带以内，最大误差为-5.07%，平均误差为-0.12%。以上结果表明：成都地区空调办公建筑回归模型预测的月总能耗、月采暖能耗和月制冷能耗具有较高精度，月采暖能耗、月制冷能耗回归模型优于月总能耗的回归模型，月制冷能耗精度最高。该模型对于预测成都地区采用变风量再热空调系统的办公建筑能耗具有一定的准确性。同时说明建筑能耗回归模型能够较好地预测由于月平均干球温度、月平均太阳辐射等5项主要气象参数的改变而产生的建筑能耗，从而为预测气候变化对建筑能耗的影响提供了便捷的方法。

5结论

对成都地区1971—2000年的气象参数进行了数据分析，模拟和分析了该地区典型空调办公建筑的能耗，建立并评价了该地区空调办公建筑月总能耗、月采暖能耗和月制冷能耗与月均干球温度、干球较差、露点温度、风速和太阳辐射5項气象参数的回归模型，分析表明：

1）建筑能耗变化不与任一气象参数呈现明显的规律性，是各项气象参数综合作用的结果。

2）建筑月总能耗与各气象参数的回归模型呈纯二次多项式关系，R2为0.804；月采暖能耗、月制冷能耗与各气象参数的回归模型呈交叉二项式关系，R2分别为0.962和0.873。

3）建筑月能耗回归模型能够较准确地预测建筑月能耗与各气象参数的关系，且月采暖能耗和月制冷能耗回归模型预测的准确性优于月总能耗模型，月总能耗、月采暖能耗和月制冷能耗回归模型预测值的平均误差分别为-4.06%、-1.27%和-0.12%。

参考文献：

[1] HONG T Z， CHANG W K， LIN H W. A fresh look at weather impact on peak electricity demand and energy using of buildings using 30 year actual weather data [J]. Applied Energy， 2013，111： 333350.

[2] SOLOMON S， QIN D， MANNING M， et al. IPCC. Climate change 2007： the physical science basis. Contribution of the working group I to the fourth assessment report of the Intergovernmental Panel on Climate Change [M]. Cambridge： Cambridge University Press， 2007.

[3] LEVINE M， URGEVORSATZ D， BLOK K， et al. Residential and commercial buildings. Climate change 2007： mitigation. Contribution of working group III to the fourth assessment report of the Intergovernmental Panel on Climate Change [M]. Cambridge： Cambridge University Press， 2007.

[4] STRAM D O， FELS M F. The applicability of PRISM to electric heating and cooling [J]. Energy and Buildings， 1986， 9（1/2）： 101110.

[5] ZMEUREANU R. Assessment of the energy savings due to the building retrofit [J]. Building and Environment， 1990， 25（2）： 95103.

[6] KISSOCK J K， REDDY T A， CLARIDGE D E. Ambienttemperature regression analysis for estimating retrofit savings in commercial building [J]. Journal of Solar Energy Engineering， 1998， 120（2）： 168176.

[7] KISSOCK K， JOSEPH H B， MCBRIDE J. The effects of varying indoor air temperature and heat gain on the measurement of retrofit savings [J]. ASHRAE Transactions， 1998，104 （2）： 895900.

[8] VIPUL S， AGAMI R T， BASS A. Predicting annual energy use in buildings using shortterm monitoring： the drybulb temperature analysis （DBTA） method [J]. ASHRAE Transactions， 2014， 120（1）： 397.

[9] MASON M D， KINGSTON T M. Let's talk about weather [C]//Proceedings of the Building Simulation 93： 487494.

[10] DAY A R. An improved use of cooling degreedays for analysing chiller energy consumption in buildings [J]. Building Services Engineering Research & Technology， 2005， 26（2）： 115.

[11] ROSA M D， BIANCO V， SCARPA F， et al. Heating and cooling building energy demand evaluation； a simplified model and a modified degree days approach [J]. Applied Energy， 2014， 128： 217229.

[12] DOMBAYCI A， OZTURK H K. The prediction of fuel and energy consumption by using degreedays method for residential buildings in Denizli [J]. International Journal of Materials Science and Application， 2016， 5（6）： 610.

[13] 沈昭華，谭洪卫，吕思强，等. 上海地区建筑能耗计算用典型年气象数据的研究[J]. 暖通空调，2010，40（1）：8994.

SHEN Z H， TAN H W， LV S Q， et al. Research on the typical meteorological year data of Shanghai for the building energy consumption calculation [J]. HV&AC， 2010， 40（1）： 8994. （in Chinese）

[14] EnergyPlus supplement， version 8.1 [M]. Lawrence Berkeley National Laboratory， University of California， 2013.

[15] 袁志发，宋世德.多元统计分析[M].北京：科学出版社，2009.

YUAN Z F， SONG S D. Multivariate statistical analysis [M]. Beijing： Science Press， 2009. （in Chinese）

[16] 谢中华.MATLAB统计分析与应用[M].北京：北京航空航天大学出版社，2015.

XIE Z H. MATLAB Statistical analysis and application [M]. Beijing： Beijing University of Aeronautics and Astronautics Press， 2015.