超混沌系统精确反馈线性化耦合混沌同步

李 钢， 魏 爽， 乔红玉， 康轶薇， 王忠鑫， 马 翔， 张晓璇

(辽宁师范大学 物理与电子技术学院， 辽宁 大连 116029)



超混沌系统精确反馈线性化耦合混沌同步

李 钢， 魏 爽， 乔红玉， 康轶薇， 王忠鑫， 马 翔， 张晓璇

(辽宁师范大学 物理与电子技术学院， 辽宁 大连 116029)

基于微分几何理论，在仿射型误差动力学方程引入耦合控制来扩充多输入多输出系统的向量相对阶，进而通过全部状态变量反馈线性化使其变换为线性可控的系统.在外环和线性耦合的组合控制下，实现了两个混沌系统之间的完全同步.以超混沌Chen系统为例提出了同结构混沌同步的控制方案，模拟仿真验证了方案的有效性.对于异结构混沌同步以及其他混沌同步类型的应用有较强的适用性.

混沌同步；微分几何；精确反馈线性化；向量相对阶

基于微分几何方法对非线性系统的精确反馈线性化，为混沌控制与同步的理论研究提供了一个有效的分析工具[1-2].近10年来，精确反馈线性化在混沌控制与同步研究中受到较多的关注[3-12]，但多是采用单输入单输出的控制方式[6-10]，选择多输入多输出控制的文献尚不多见[11-12].传统的近似线性化控制方法一般仅在平衡点附近的邻域内有效，而精确反馈线性化的方法由于没有忽略高阶非线性项而能够适用于整个变换区域，且能够获得更好的动态性能和稳定性.尤其是多输入多输出的控制方式在控制器的设计上还具有较大的灵活性，如融合其他镇定方法，可以在混沌同步控制研究中获得广泛的应用.

此外，在多输入多输出仿射型混沌系统中，对于不同控制和输出的选择会使系统具有不同的向量相对阶，若其小于系统的维数，只能获得部分状态的线性化和不能线性化的系统内动态，系统的稳定性问题将取决于系统的内动态.如依据系统非线性特征适当选择控制和输出，才有可能使系统的向量相对阶与系统的维数相同，从而实现全部状态变量的线性化.

基于微分几何理论研究同结构超混沌系统的同步问题，在对多输入多输出仿射型误差动力学系统非线性特征的分析以及对控制和输出错位选择的基础上，在响应系统的适当位置引入线性耦合以期扩充误差动力学系统的向量相对阶至与系统的维数相同，从而使误差动力学系统实现全部状态的线性化，然后通过线性耦合系数和外环控制系数的调节来实现同结构超混沌系统的完全同步.最后，用模拟仿真来验证了控制方案的有效性.

1 同步控制原理

两个混沌系统的误差动力学方程可以表述为如下多输入多输出仿射型非线性系统.

(1)

其中，e=y-x为两系统的误差状态变量，x,y,e∈U⊂n，x和y分别为驱动系统和响应系统的状态变量向量，U是流形N=n上的一个开集；f(e),g1(e),…,gm(e)∈n为定义在U上的光滑向量函数；u=[u1,u2,…,um]T∈J为m维输入向量，J是允许控制集；h(e)=[h1(e),h2(e),…,hp(e)]T∈Y为输出向量函数，Y则是p维实值函数组成的线性空间.

计算系统(1)的向量相对阶.在多数的情况下，系统的向量相对阶往往小于系统的维数，有时需要用特殊方法加以扩充，如动态扩充方法[13]，但这会增加系统的设计成本.这里采用通过在响应系统中的适当位置上引入线性耦合的方式，将系统的向量相对阶调整到与系统同维，即r1+r2+…+rm=n，使系统满足状态空间精确线性化问题的基本充要条件[13]，以便对系统进行全部状态变量反馈线性化.通过李导数的运算[11]，得到如下m组非线性变换的函数集.

(2)

从而可把原系统(1)变换为m组方程：

(3)

上述的非线性坐标变换不会改变系统的相对阶.方程组(3)中的最后一式展开写为矩阵形式：

(4)

由于系统的向量相对阶等于系统的维数，则式(4)中的矩阵A(ξ)在e0=φ-1(ξ0)的邻域内是非奇异的.因此，若令控制器形式为

u=A-1(ξ)(vi-b(ξ)).

(5)

则原系统转换为Brunovsky标准型：

(6)

即实现了精确反馈线性化.其中,vi是施加的外环反馈控制[13]，目的是在与线性耦合系数的共同调节下使上述线性化后的系统渐进稳定于误差动力学系统的零点，即实现两个混沌系统的同步.vi的形式:

(7)

2 同结构超混沌Chen系统混沌同步

分别作为驱动系统和响应系统的超混沌Chen系统:

(8)

当参数a=35、b=3、c=12、d=7和r=0.5时，超混沌Chen系统处于混沌状态.式(8)中的u1和u3是待定控制器，u2=k1(y1-x1)和u4=k2(y3-x3)是根据系统非线性特征而在适当位置引入的线性耦合控制，在它们与u1和u3的共同作用下以及对于相应误差动力学系统中选择的输出相配合可以将误差系统的向量相对阶调整至与系统维数相同，还可以为系统的渐进稳定提供调节参数.由状态变量误差的定义e=y-x得到如下相应于式(1)的仿射型多输入多输出误差动力学系统.

(9)

其中,

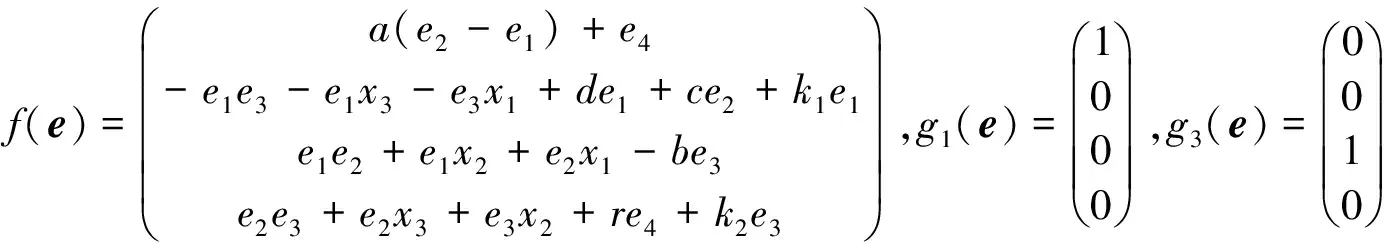
(10)

选择两个输出函数L1=h1(e)=e2和L2=h2(e)=e4，可以验证，对于这两个输出通道的相对阶分别为r1=2和r2=2，即该系统的向量相对阶与系统维数相同，满足反馈线性化的基本充要条件.由此获得相应于式(2)的坐标变换和反馈线性化过程中式(4)的结果.

(11)

(12)

其中,

(13)

(14)

(15)

由式(12)可以获得精确反馈线性化的控制器.则

(16)

其中,

(17)

图1 两个超混沌系统的误差变量随时间的演化Fig.1 Evolution of the error variables between two chaotic systems with time

3 结 论

微分几何理论应用于混沌同步控制中，具有控制区域大，动态响应迅速的特点.在响应系统中的适当位置引入线性耦合控制的方式可以灵活地改变误差动力学系统的向量相对阶，适应不同多输出的选择，使在控制器的设计中能够将全部误差状态变量精确反馈线性化，避免处理内动态问题.模拟仿真的结果表明，尽管混沌系统具有较为复杂的非线性结构，但基于微分几何理论的精确反馈线性化通过与其他传统控制方法相结合，对于多输入多输出仿射型混沌系统的各类混沌同步控制问题有着较为广泛的适用性.

[1] GINOUX J M,ROSSETTO B.Differential geometry and mechanics:applications to chaotic dynamical systems[J].International Journal of Bifurcation and Chaos,2006,16(4):887-910.

[2] LI H T,YANG S,REN H L.Dynamic decoupling control of DGCM gimbal system via state feedback linearization[J].Mechatronics,2016,36:127-135.

[3] 韦笃取,罗晓曙,方锦清,等.基于微分几何方法的永磁同步电动机的混沌运动的控制[J].物理学报,2006,55(1):54-59.

[4] SALARIEH H,SADEGHIAN H,MERAT K.Chaos control in lateral oscillations of spinning disks via nonlinear feedback[J].Nonlinear Analysis:Real World Applications,2009,10:2864-2872.

[5] ZHANG J,XU D L,ZHOU J X,et al.Chaotification of vibration isolation floating raft system via nonlinear time-delay feedback control[J].Chaos,Solitons and Fractals,2012,45(s9/10):1255-1265.

[6] ZHANG T,WANG J,FEI X Y,et al.Synchronization of coupled FitzHugh-Nagumo systems via MIMO feedback linearization control[J].Chaos,Solitons and Fractals,2007,33(1):194-202.

[7] 朱志宇.基于反馈精确线性化的混沌系统同步控制方法[J].物理学报，2006,55(12)：6248-6252.

[8] 陈明杰,张爱筠.基于微分几何理论的混沌同步研究[J].哈尔滨工程大学学报,2007,28(5):536-541.

[9] YAN J P,LI C P.On chaos synchronization of fractional differential equations[J].Chaos,Solitons and Fractals,2007,32(2):725-735.

[10] 李钢,王水,张吉泉，等.基于微分几何理论的Rossler混沌系统同步研究[J].辽宁师范大学学报(自然科学版),2015,38(2):179-183.

[11] 王智良,张化光.基于非线性反馈控制的高维混沌系统同步[J].东北大学学报(自然科学版),2002,23(2):126-129.

[12] 赵辽英,赵光宙,厉小润.基于非线性反馈控制的超混沌系统同步方法[J].浙江大学学报(工学版),2004,38(5):544-548.

[13] 李殿璞.非线性控制系统理论基础[M].哈尔滨：哈尔滨工程大学出版社，2006：284-291,265,249.

Chaos synchronization by the exact feedback linearization for the coupled hyperchaotic system

LIGang,WEIShuang,QIAOHongyu,KANGYiwei,WANGZhongxin,MAXiang,ZHANGXiaoxuan

(School of Physics and Electronic Technology, Liaoning Normal University, Dalian 116029, China)

Based on the differential geometry theory, the linearly coupled control is introduced into the MIMS affine error dynamical system to extend its vector relative degree so that the system can be transformed as a linearly controllable one by the exact feedback linearization.Then,the chaos synchronization is realized by the hybrid control of the coupling and outer loop.The controllers are designed for the hyperchaotic Chen system as an example. The simulation results indicate that the proposed scheme works well.This method is suitable for the chaos synchronization between the different chaotic systems and for the different type.

chaos synchronization;differential geometry;exact feedback linearization;vector relative degree

2016-12-28

李钢(1959-)，男(朝鲜族)，黑龙江绥化人，辽宁师范大学教授.E-mail:lglhc@163.com

1000-1735(2017)02-0182-05

10.11679/lsxblk2017020182

O415.5

A