对脉冲多普勒雷达的多相位分段调制干扰方法*

吴彦鸿，俞道滨，王宏艳，贾鑫

(装备学院，北京 101416)

对脉冲多普勒雷达的多相位分段调制干扰方法*

吴彦鸿，俞道滨，王宏艳，贾鑫

(装备学院，北京 101416)

针对部分相参干扰的信号设计问题，提出一种基于多相位分段调制的干扰方法，对其原理进行详细说明，给出了干扰输出的数学推导，得到多矢量叠加的结果。以脉冲多普勒雷达为例，分析脉间多相位分段调制干扰在多普勒域的干扰效果，通过对调制参数的设置可以得到范围可控的局部遮盖效果。最后进行仿真验证，说明应用该干扰技术能够在多普勒域产生遮盖效果，有效破坏雷达对目标速度信息的获取。

部分相参干扰；信号设计；多相位分段调制；多矢量叠加；脉冲多普勒雷达；局部遮盖

0 引言

脉冲多普勒(pulsed Doppler，PD)雷达是在动目标显示雷达基础上发展起来的一种全相参体制雷达，其通过发射相参脉冲串信号，并在接收端通过相参积累、频域滤波技术，能够在强杂波背景中检测、跟踪运动目标[1-2]。当前，对PD雷达的干扰主要应用转发式干扰机实现，通过生成全相参或部分相参信号，可以在接收机处获得较大的处理增益，在目标附近形成与其特征相近的假目标[3-5]。当前，针对PD雷达的主要干扰样式包括：距离波门拖引干扰、速度波门拖引干扰、假多普勒频率干扰、多普勒频率闪烁干扰和距离-速度同步拖引干扰(包括匀速拖距干扰和匀加速拖距干扰)[6-7]等。其中，利用数字射频存储器(digital radio frequency memory，DRFM)作为控制核心，产生相参干扰信号，实现对PD雷达的转发式欺骗干扰[8-10]。当相参干扰的规律性被抗干扰方利用，其效果会有所降低[11]，而部分相参干扰也是一种有效的干扰手段，通过对干扰信号参数的灵活设计，能够产生欺骗和压制双重干扰的效果，典型部分相参干扰如灵巧噪声干扰、间歇采样干扰等[12-15]。

本文提出一种基于多相位分段调制的PD雷达干扰技术，是一种二维参数控制下的部分相参干扰技术，通过破坏雷达信号的相干性，从而影响其对速度信息的获取。首先，给出信号多相位分段调制的原理及流程，分析多相位分段调制干扰信号在多普勒域的输出结果，最后进行仿真验证。

1 多相位分段调制干扰

1.1 调制原理

对雷达信号的多相位分段调制，即在信号的不同时间分段上调制不同的相位值，得到相应的干扰信号。对该干扰调制样式作如下限定：

(1) 无论雷达信号为何种样式，调制后生成的干扰信号与原信号的时间长度相等。

(2) 多相位指代的调制相位值可以取[0，2π]上的任意值，取值个数≥2，且数量为有限个。

(3) 分段指代的信号时间长度可以是小于原信号长度的任意值，且对分段的规则可以是等分的，也可以是非等分的。

在上述规则的限定下，可以将该类信号调制视为一个在相位-时间平面上的二维赋值过程，其中x轴表示调制相位值的大小，y轴表示信号分段的长度。以三相位非等分调制为例，在时间-相位二维平面上，信号的多相位分段调制原理如图1所示。

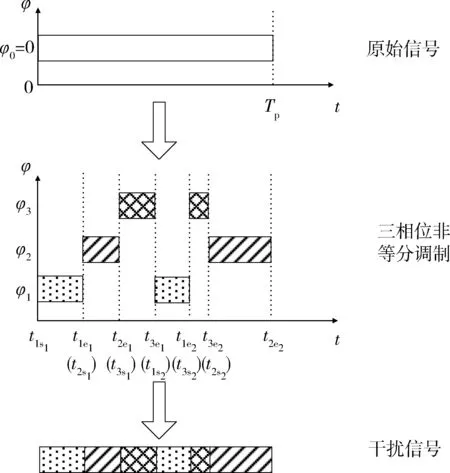
图1 多相位分段调制原理示意图Fig.1 Schematic diagram of multiple phase sectionalized modulation (MPSM)

由以上原理可知，多相位分段调制为由二维参数组合控制下的干扰样式。

1.2 脉间调制信号分析

干扰信号表达式与信号分段的长度和数量、调制相位值的大小和顺序有关。设原信号为s(t)，调制相位值分别为φ1，φ2，φ3，设在整个信号调制过程中，调制相位值为φ1的所有信号分段的起始和截止时刻分别为t1si，t1ei，其余信号分段起始和截止时间点定义方法与第一路的类似。在上述参数说明的基础上，将分段信号间的调制相位值跳变用阶跃函数ε(t)来表示，得到的输出结果相当于原信号与复合函数相乘，即

(1)

式中：

(2)

式中：n1，n2，n3分别为调制相应相位值的信号分段数，以图1为例，n1=n2=n3=2。分段时间起始点和分段数量确定后，即可得到最终的干扰信号表达式。对于脉间多相位分段调制，其原理如图2所示。

设脉冲信号长度为Tp，脉冲重复间隔为T。作脉间多相位分段调制后，对第i个调制相位值为φp的脉冲而言，设其之前已有k个脉冲，此时该脉冲的时间起始点可写为

(3)

此时，脉间调制复合函数的表达式为

(4)

图2 脉间多相位分段调制原理Fig.2 Inter-pulse multiple phase sectionalized modulation

由以上原理可知，多相位分段调制为由二维参数组合控制下的干扰样式，干扰信号表达式与信号分段的长度和数量、调制相位值的大小和顺序有关。在下文中的讨论中，以PD雷达为对象，重点分析在调制相位值大小固定的情况下，由分段数量(或长度)与相位值顺序组合变化得到的干扰样式及其效果。

2 对PD雷达的干扰分析

对接收的雷达信号作多相位分段调制后，假设目标回波与干扰信号均在主瓣内，雷达对二者的处理过程相同。对自卫式干扰，干扰机置于目标上，二者具有相同的运动规律。下面分析对目标速度估计的干扰效果。

(5)

式中：Rc为天线与目标的最短斜距。将该距离表达式代入，可以得到目标回波信号的表达式为

(6)

式中：G和σ分别为天线增益和目标散射系数，为简化分析将其视为常数。

式(6)中的第1项决定了运动目标所在的距离单元，第二项决定了运动目标的运动特性。设此时运动目标位于某一特定距离单元中，雷达对其照射的驻留时间为M个脉冲。将回波信号表示为

(7)

式(7)表示脉间信号是离散的。由于干扰信号是在回波基础上作调制，调制相位使信号产生多普勒频偏，对于脉间调制而言，在计算调制相位的变化率时，需考虑脉宽与脉冲重复间隔的比值的影响。此时附加的多普勒频偏为

(8)

(9)

式中：下标k=1，2，…，p表示对应的p个相位调制值产生的频偏。考虑相位调制的时序，引入相位调制函数进行分析，由于此时信号为离散函数，对调制函数作离散时间傅里叶变换，得到干扰信号的频域表达式为

(10)

对于相位调制值为φ1的所有项而言，当采样点间隔符合均匀随机分布特征时，采样点间隔可近似取为(p-1)βT。上述累加式的第1项可写为

(11)

式中：f∈[-PRF/2，PRF/2]，PRF为雷达工作的脉冲重复频率。

对于多相位分段调制干扰信号而言，由于干扰机置于目标上，其运动变化规律与目标一致。已知n1，n2，…，np分别表示调制相应相位值的信号分段数，且n1+n2+…+np=N，则对于具有p个相位值N个分段的调制信号，干扰信号在多普勒域的表达式为

(12)

由式(12)可知，Sk(f)的幅值和相位与调制各分段数量nk和调制相位产生的多普勒频移fk均相关，为在多普勒域p个信号矢量的叠加。当信号分段数nk变大时，矢量幅值减小，输出的信号峰值会下降，且各个零点之间的间距不断扩大。在一定的干信比下，该输出峰值与目标回波处理峰值产生混叠效应，破坏对目标真实速度的获取。

3 仿真校验

下面对多相位分段调制信号在多普勒域的干扰效果进行仿真分析。设置一匀速运动的目标，PD雷达的仿真参数如表1所示。经计算，对应的雷达无模糊距离等于36 km，目标设置于无模糊距离以内，对应于第166个距离采样点，在该特定距离单元内，给出MTD结果，如图3所示。无干扰时，0.64×PRF=5.3 kHz，与目标运动的多普勒频率吻合，可以对目标速度进行准确的估计，其中PRF表示脉冲重复频率。

表1 PD雷达仿真参数Table 1 Simulation parameters of PD radar

图3 无干扰时的MTD结果Fig.3 MTD results without jamming

将干扰机置于目标上，其具有与该目标相同的运动特性，干扰机及多相位分段调制的仿真参数如表2所示。设置脉间调制样式为四相位均匀分段随机交织，分别设置5，10，25个信号分段，信号长度分别为10，5，2个脉冲，得到的调制相位值与脉冲数的关系如图4a所示，相同距离单元内有无干扰时的MTD结果分别如图3，4所示(干信比均为10 dB)。其中，信号幅度与采样率、信号长度等参数有关，此处仅为显示干扰参数变化时幅值的相对变化，故不标注量纲。

图4 调制相位变化及相应的MTD干扰效果Fig.4 Variation of MPSM and the MTD jamming effects

参数名称取值干扰机离雷达距离/km5干扰机飞行速度/(km·s-1)0.3调制相位值/rad0,π/2,π,3π/2

由仿真结果分析可知，脉间多相位分段调制破坏了脉冲信号间的相参性，对目标的多普勒频移参数估计会产生一定的偏差，包括峰值的大小、位置、宽度等。

以四相位五分段调制的情况为例进行说明：

(1) 当无干扰时，真实目标信号的峰值为6 042，出现在0.64倍PRF处，其3 dB宽度为0.04倍PRF；

(2) 当存在干扰且其强于回波信号时，一方面，由公式(8)计算干扰信号峰值位置，此时由调制相位值计算得到的多普勒频偏fk有4个，则

(13)

由于干扰信号为单程，计算干扰信号频移：

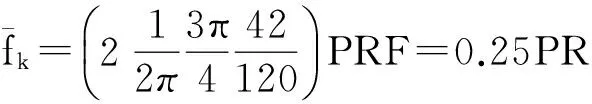
(14)

峰值出现的中心位置约为0.64-0.25=0.4倍的PRF处。

另一方面，由于为5分段，由sinc函数性质可知，峰值宽度约为5×0.04=0.2倍的PRF。

需要指出的是，由式(12)可知，最终输出信号为各分段信号的矢量叠加。由仿真结果可知，随着信号分段数的增加，输出峰值降低，不同频点上的峰值数量增多。由该仿真结果可知，在较大干信比条件下(此处为10 dB)，可以增多调制的信号分段数，在真实目标附近产生扰乱效果。如图4，在25个信号分段时，干扰信号产生的峰值与真实目标峰值高度相近，即生成的干扰点较多且与目标的速度相近，此时得到的干扰效果最佳。

由以上仿真结果可知，通过多相位分段调制可以破坏雷达信号的脉间相干性，从而影响对真实目标多普勒频移的参数估计，达到对PD雷达进行干扰的目的。

4 结束语

本文提出了一种基于多相位分段调制的PD雷达干扰方法，分析了多相位分段调制干扰的效果。分析表明，该干扰信号输出为多矢量叠加的结果，能够有效破坏雷达对目标速度信息的获取。由仿真结果可知，该干扰方式需结合干信比参数，对干扰信号的调制相位值和信号分段数进行设计，从而能够在真实目标附近产生速度相近的多干扰点局部遮盖效果，是一种有效的干扰方法。

[1] 丁鹭飞.雷达原理[M].4版.西安：西安电子科技大学出版社，2009. DING Lu-fei.Radar Principle[M].4th ed.Xi’an：Xidian University Press，2009.

[2] 向敬成.雷达系统[M].北京：电子工业出版社，2001. XIANG Jing-cheng.Radar System[M].Beijing：Publishing House of Electronic Industry，2001.

[3] SCHLEHER D C.Electronic Warfare in the Information Age[M].America：Artech House，1999.

[4] 赵国庆.雷达对抗原理[M].西安：西安电子科技大学出版社，1999. ZHAO Guo-qing.Radar Countermeasures Principle[M].Xi’an：Xidian University Press，1999.

[5] LI Neng-jing，ZHANG Yi-ting.A Survey of Radar ECM and ECCM[J].IEEE Transactions on Aerospace and Electronic Systems，1995，31(3)：1110-1119.

[6] 郑继刚，用数字储频进行距离和速度波门同步拖引的实现方法[J].舰船电子对抗，1999(6)：14-17. ZHENG Ji-gang.The Realization of Range and Velocity gate Synchronization Pulling off Deception Based on DRFM Technique[J].Shipboard Electronic Warfare，1999(6)：14-17.

[7] 王跃鹏，黄建冲.对PD雷达进行距离和速度波门同步拖引的DRFM实现方法[J].电子对抗，2004(5)：15-19. WANG Yue-peng，HUANG Jian-chong.Range and Velocity Gate Synchronization Pulling off Deception Based on DRFM Technique to PD Radar[J].Electronic Warfare，2004(5)：15-19.

[8] 刘勇.基于DRFM的PD雷达干扰技术及其实现[D].长沙：国防科学技术大学，2006. LIU Yong.The Jamming Technique and Its Realization Based on DRFM for PD Radar[D].Changsha：National University of Defense Technology，2006.

[9] 孙智勇，唐宏，余定旺，等.基于DRFM的机载PD雷达干扰研究[J].现代防御技术，2012，40(4)：138-142. SUN Zhi-yong，TANG Hong，YU Ding-wang，et al.Interference on Airborne PD Radar Using DRFM-Based Technique[J].Modern Defense Technology，2012，40(4)：138-142.

[10] ROOME S J.Digital Radio Frequency Memory[J].Electronics and Communication Engineering Journal，1990，2(8)：147-153.

[11] 王健，王宝，万华.脉冲多普勒雷达同频干扰研究[J].雷达科学与技术，2014，12(4)：441-445. WANG Jian，WANG Bao，WAN Hua.Study on Co-Frequency Interference Between Pulse Doppler Radars[J].Radar Science and Technology，2014，12(4)：441-445.

[12] 邬诚，颜振亚.噪声调制灵巧噪声对雷达干扰性能研究与实现[J].现代雷达，2014，36(7)：77-80. WU Cheng，YAN Zhen-ya.Study on Performance and Implementation of Smart Noise to Radar Based on Noise Modulation[J].Modern Radar，2014，36(7)：77-80.

[13] 邱杰，邱丽原.灵巧噪声干扰本质及相关基本问题探讨[J].现代防御技术，2012，40(3)：132-136. QIU Jie，QIU Li-yuan.Essential Signification of Smart Noise Jamming[J].Modern Defense Technology，2012，40(3)：132-136.

[14] 李大强，李修和，沈阳，等.一种灵巧的多假目标干扰技术研究[J].现代防御技术，2010，38(3)：108-113. LI Da-qiang，LI Xiu-he，SHEN Yang，et al.A Smart Multiple False Target Jamming Technique[J].Modern Defense Technology，2010，38(3)：108-113.

[15] 隋鉴，李国林，尹洪伟.脉冲多普勒引信的速度多假目标干扰[J].电光与控制，2015，22(10)：7-9. SUI Jian，LI Guo-lin，YIN Hong-wei.Multiple Speed False Targets Jamming by Pulse-Doppler Fuze[J].Electronics Optics and Control，2015，22(10)：7-9.

Multiple Phase Sectionalized Modulation Jamming Method for Pulse Doppler Radar

WU Yan-hong，YU Dao-bin，WANG Hong-yan，JIA Xin

(The Equipment Academy，Beijing 101416，China)

For signal's design problem in partial coherent jamming, a new method based on multiple phase sectionalized modulation(MPSM) is proposed. The principle of MPSM is elaborated firstly, and the inter-pulse jamming signal generation is derived in details, where the multi-vector’s superposition is obtained. Taking a typical coherent radar-PD radar as an example, the jamming effect after MPSM is analyzed in Doppler region, and the partial overspread effects are controlled by adjusting modulation parameters. Finally, the simulation is conducted to prove the related analysis above, and it is obvious that this jamming technique can produce plenty of false targets for partial confusion and will jam the speed information acquisition of real targets.

partial coherent jamming；signal design；multiple phase sectionalized modulation；multi-vector’s superposition；pulse Doppler radar；partial overspread

2016-07-13；

2016-09-10

吴彦鸿(1971-)，男，甘肃靖远人。教授，博士，主要从事雷达信号处理方面研究。

通信地址：101416 北京市怀柔区八一路1号 E-mail：mail2wyh@163.com

10.3969/j.issn.1009-086x.2017.03.013

TN974；TN766.5；TP391.9

A

1009-086X(2017)-03-0081-06