弹道导弹主动段变换打击目标的闭路制导研究*
2017-06-27范金龙刘新学武健夏维
范金龙,刘新学,武健,夏维
(火箭军工程大学 初级指挥学院,陕西 西安 710025)
弹道导弹主动段变换打击目标的闭路制导研究*
范金龙,刘新学,武健,夏维
(火箭军工程大学 初级指挥学院,陕西 西安 710025)
提出了弹道导弹主动段变换打击目标的概念。为了实现弹道导弹变换打击目标的制导目的,提出了基于网格离散的闭路制导方法。将二级段和可攻击区域进行网格离散,把节点插值参数存储到弹上。导弹在变换打击目标时,通过插值的方法求解需要速度,进行闭路制导。仿真结果表明,该方法能够有效控制导弹完成变换打击目标的任务,制导精度较高。
弹道导弹;主动段;变换目标;空间离散;插值求解;需要速度;闭路制导
0 引言
随着战争信息化的快速发展,战争对武器的实时性控制要求越来越高。弹道导弹具有射程远、精度高、威力大的特点,担负核威慑、核反击和远程火力打击等任务。当敌方发动核袭击时,预警系统发出预警信号,我方发射核导弹进行核反击。但是,在特殊情况下,当预警系统可能发出错误信号后,如果我方核导弹已经发射,应立即变换目标使核弹头落入安全地点,从而尽量避免发生核战争;其次,常规作战中,当导弹发射后,如果目标的打击可能性或毁伤价值下降,可以通过卫星传达指令,临时变换打击目标,选择其他高价值目标作为打击对象,从而提高导弹的利用效能。综上所述,弹道导弹主动段变换打击目标可能成为未来战争的需求,因此具有一定的研究价值。
闭路制导是在导航计算的基础上,利用需要速度的概念将导弹当前位置和目标位置联系起来的一种制导方法[1]。相对摄动制导方法,精度更高,对标准弹道的依赖度降低,可以满足一定范围内的机动飞行要求。在导弹发射前,根据标准弹道,对再入阻力和地球引力扁率影响进行修正,产生虚拟目标[2]。导弹在飞行中变换打击目标时,弹上难以根据导弹的实时位置和新目标点计算出新的虚拟目标,因此,传统的闭路制导方法难以实现变换打击目标的目的。
本文提出基于空间网格[3]的闭路制导方法,射前根据发射任务,计算导弹飞行所经区域空间节点的数据,导弹在飞行中变换打击目标时,利用射前装订的节点数据插值求解导弹对新目标的需要速度,进行闭路制导[4-5]。该方法计算量较小,能够满足远程和洲际弹道导弹在主动段变换打击目标的制导要求。
1 基本思想
远程弹道导弹的闭路制导在主动段二级飞行中进行[6],导弹二级飞行稳定、速度较大并且时间较长,在进行闭路制导时,具备变换打击目标的可能。基于空间网格的闭路制导需要完成4个方面的主要工作。
第1,确定导弹二级所处的位置以及某一位置下导弹的大致速度。假设导弹在一个阵地上可以向任意方位的目标进行打击,导弹的射程可以从最小射程到最大射程,确定位置和速度大致范围,用于主动段空间位置和需要速度离散,求解导弹的可攻击范围。
第2,求解实时可攻击范围。导弹在变换目标时,首先确定导弹的实时可攻击区域,在可攻击区域以内的目标可以进行攻击,如果目标在攻击范围以外则不能进行攻击。
第3,准确求解需要速度。基于虚拟目标的需要速度求解方法计算量大,且目标变化时需重新求解虚拟目标。文章提出基于落点的需要速度计算方法,可以较快的计算导弹的需要速度,且发射点和目标可变化。通过仿真求解需要速度随空间位置和目标点经纬度的变化规律,并将插值多项式的系数存储到节点上。
第4,实时求解需要速度。导弹在空中[7]变换打击目标时,判断目标位置和导弹的空间位置,调用节点参数,插值求解导弹的需要速度,进行闭路制导。具体如图1所示。
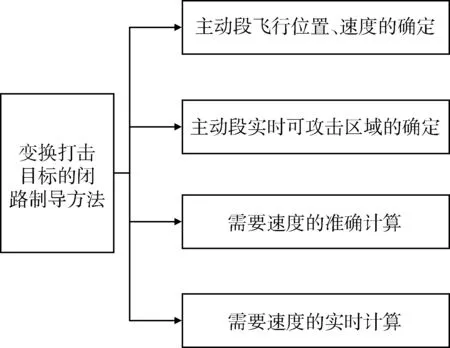
图1 变换打击目标的主要工作Fig.1 Main work of changing attacking target
2 模型建立
2.1 导弹的运动模型
根据导弹在飞行中的受力,在发射坐标系下建立导弹的质心运动方程[8]。
导弹主动段质心运动模型如下:
(1)
导弹被动段质心运动模型[9]如下:
(2)
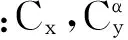
2.2 确定导弹主动段飞行空间位置、速度
本文将网格离散的方法用于闭路制导,首先要确定导弹在主动段[10]二级飞行时的空间位置和速度的大致范围,在大致范围内对导弹的空间位置和速度进行离散。
射向是导弹发射前,依据目标的位置,获取导弹的天文瞄准方位角来确定的;射程通常是通过控制导弹的飞行程序来实现的。
在飞行程序的设计中,通常使用工程设计法,依据经验公式对导弹的飞行程序进行设计。为了获得导弹的飞行程序,通常先确定导弹的攻角,然后,通过式(3)计算导弹的飞行程序。
(3)

攻角α随时间的变化关系通常由经验公式确定,经验公式为
(4)

通过模拟试飞获得导弹位置、速度的节点关系,在此情况下求解在位置变化时速度的相应变化规律,通过插值的方法求解节点之外位置的速度。在位置和速度对应关系确定之后,求解导弹在此位置的可攻击范围。具体求解导弹主动段位置、速度的方法如图2所示。
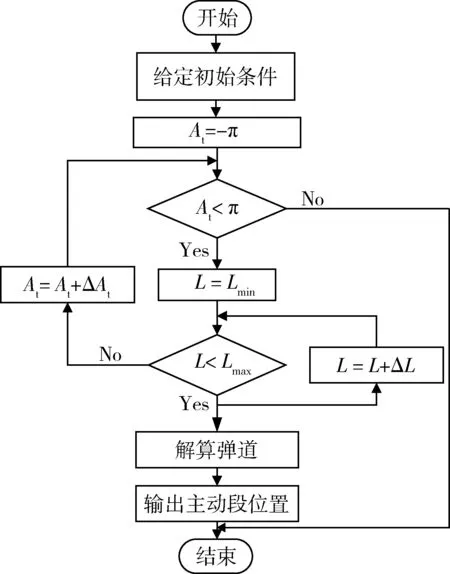
图2 主动段位置、速度范围确定流程图Fig.2 Flowchart of computing location and velocity in boost phase
确定导弹二级飞行时的大概位置和速度后,为求解导弹的可攻击区域做数据准备。
2.3 导弹主动段机动可攻击区域确定
弹道导弹在主动段变换打击目标时,首先要确定当前状态下导弹的可攻击区域[11]。导弹的实时可攻击区域是导弹性能参数和当前参数的隐函数,可表示为
(5)
式中:S为导弹的可攻击区域;p为发动机的推力矢量;v为导弹的速度矢量;r为导弹的位置矢量;nmax是导弹的过载最大值;α为导弹的攻角;β为导弹的侧滑角;tg为二级发动机的剩余工作时间;hm为落点的平均高程;n1,n2为其他可能的约束条件,例如导弹控制系统偏差,测量元器件偏差,外界风场、电磁异常等影响,由于这些影响难以预测并且影响较小,在仿真中将不予考虑。
导弹的机动飞行受到导弹性能的限制,主要有导弹的过载不能超过最大过载,控制力矩不能超过最大控制力矩,头体分离时攻角尽可能小等。
假设导弹的攻角α的最大值为αmax,侧滑角β的最大值βmax,二级发动机当前状态的剩余工作时间为tg。攻角和侧滑角在极限范围内变化可求得导弹在当前状态下的可攻击区域。可攻击区域的求解流程如图3所示。
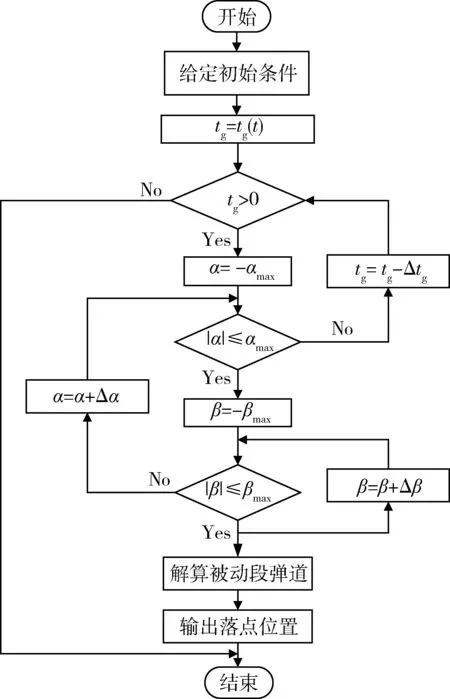
图3 可攻击区域的求解流程图Fig.3 Flowchart of computing dynamical attack zone
通过数据仿真,求解导弹在某一时刻下的可攻击区域,将可攻击区域的插值参数存储到弹上,以便实时求解导弹的可攻击区域,用以判断导弹的新目标点是否在可攻击区域以内。
2.4 节点需要速度的准确确定
在对空间网格离散后,计算空间节点的需要速度,主要工作都是在导弹发射之前完成的,因此在计算需要节点需要速度时应该尽量提高计算的精度。
传统的闭路制导方法,利用射前装订的虚拟目标和导弹飞行中实时的位置矢、速度矢,根据椭圆弹道理论,求解导弹的需要速度,计算量较小,适合弹上使用。但是当导弹偏差较大或者进行大范围机动时虚拟目标会发生变化,进而产生较大制导偏差。因此,传统的闭路制导并且不具备变换打击目标的能力。
本文提出一种基于落点的弹道导弹需要速度求解方法,精度高,目标位置可变化,且计算量不大,能够准确求解网格节点的需要速度。该方法的基本思想是:导弹当前位置为F,在无推力作用下的落点[12]为L,新目标为M,以导弹初始位置F、落点L和地心O组成绝对弹道面S1[13];以落点L、地心O和弹道面,S1的法向量n1确定面S2,平面S1,S2和地球表面的交点为J。J点到M的距离为ΔH,J点到L的距离为ΔL。通过迭代逐步减小偏差,直至满足精度要求,参数关系如图4所示,求解流程图如图5所示。

图4 需要速度求解参数示意图Fig.4 Schematic diagram of computing parameters for required velocity

图5 需要速度求解流程图Fig.5 Flowchart of computing required velocity
图5中,S0为起始点F到落点L的射程,S1为起始点F到目标点M的射程;A1为起始点F到落点L的大地方位角;A2为起始点F到目标M的大地方向角。Δvx1,Δvx2为变步长法求得的x轴方向速度迭代值;Δvz1,Δvz2为变步长法求得的z轴方向速度迭代值。
2.5 需要速度的实时计算
基于落点的需要速度求解方法能够准确求解导弹的需要速度,但是求解过程中计算量较大,难以在弹上实时计算。通过仿真可得,空间区域内需要速度随空间、速度变化呈现良好的多维线性变化规律,因此可以对节点间的需要速度进行线性拟合,利用插值的方法求解空间位置的需要速度,减少弹上计算机的计算量。
在惯性坐标下,导弹的需要速度与导弹的位置有关系,与时间没有关系。为简化计算量,假设此刻导弹的速度vy固定不变,即vconst=vy,那么此时导弹的需要速度分量vx,vz是位置分量x,y,z以及vy的四维线性函数,因此vx,vz的关系式可表示为
vx=a1x+b1y+c1z+d1vy+k1,
(6)
vz=a2x+b2y+c2z+d2vy+k2.
(7)
当给定x,y,z时,式(6)可化为vx=d1vy+d10,此时用最小二乘法[14]可求得d1,d10,同理此时可求得a1,b1,c1,最后可求得常数项k1。最后,通过仿真求解,获取导弹在某一空间下导弹的需要速度随x,y,z和vy的变化关系式。

(8)
(9)
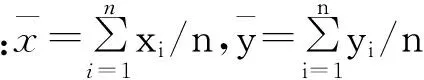
将实时可攻击区域网格化,求解主动段实时位置对网格化目标区域的节点ni,j的需要速度。如果新目标m的位置在节点上,那么直接使用空间节点的需要速度,如果目标m不在目标区域的网格节点上,那么我们可以通过插值的方法求解导弹的需要速度。
首先判断目标点m所处的网格,确定网格节点。如图6所示。

图6 落区离散示意图Fig.6 Schematic diagram of dispersed fall zone
其次,通过导弹的实时位置,判断导弹实时所处的空间网格,确定网格8个节点。利用节点所存储的信息,依次求解空间8个节点对目标m的需要速度,然后求解空间位置n对目标m的需要速度。如图7所示。
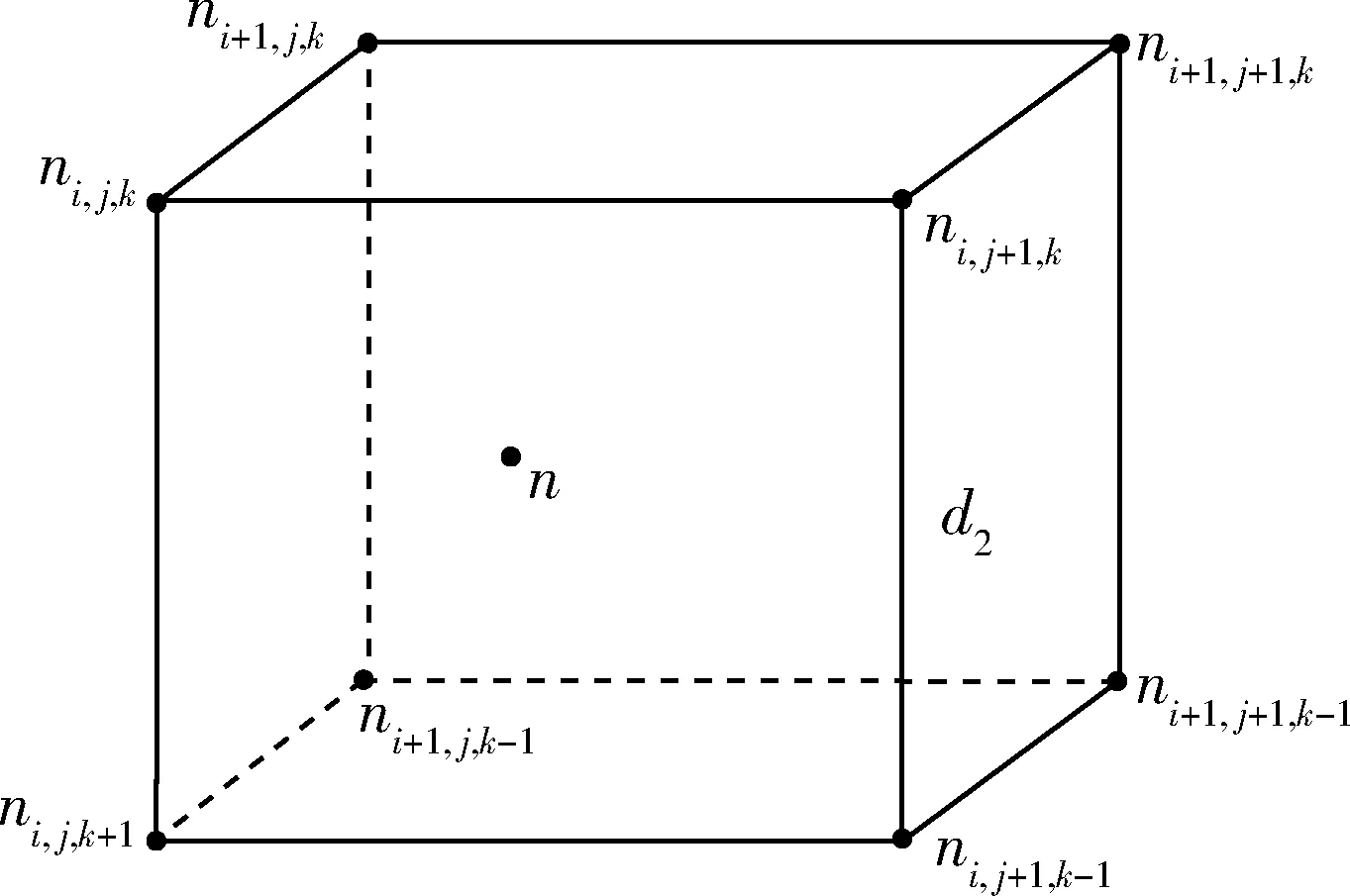
图7 空间离散示意图Fig.7 Schematic diagram of dispersed space
3 仿真验证
本文假设一种远程弹道导弹进行仿真,验证制导方法的性能。令导弹的初始打击目标为(E121°00′00″,N35°00′00″),目标区域的平均高程为2 000,令导弹的速度分量vy保持不变,导弹可攻击区域的离散粒度为d1=50 m,空间位置的离散粒度d2=100 m。
通过仿真,vx随坐标x,y,z的变化规律如图8所示,vx,vz随速度vy的变化规律如图9,10所示,vx,vz随目标点经纬度的变化规律如图11,12所示。

图8 vx随x,y,z的变化过程Fig.8 Change process of vx with x,y and z

图9 vx随vy的变化过程Fig.9 Change process of vx with vy

图10 vz随vy的变化过程Fig.10 Change process of vz with vy
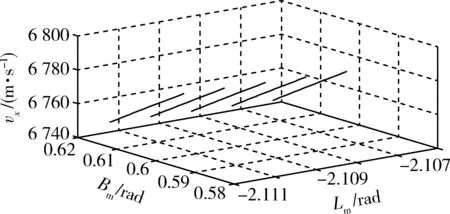
图11 vx随Lm,Bm的变化过程Fig.11 Change process of vz with Lm and Bm

图12 vz随Lm,Bm的变化过程Fig.12 Change process of vz with Lm and Bm
仿真结果显示,导弹的需要速度随参数变化呈现了较好的线性关系。利用最小二乘法求解插值多项式的参数,通过求解可得插值参数如表1所示。
导弹在进行闭路制导时首先要求解导弹的需要速度,弹上在依据节点信息进行计算时,首先要按照待增速度vgx=vgxmin,vgz=vgzmin的原则求得导弹的需要速度,然后计算发动机的控制量Δφ1,Δψ1,控制导弹飞行。当待增速度vgx<ε,vgz<ε(ε为小量)时,发动机关机。

表1 插值多项式的参数Table 1 Interpolation polynomial parameters
通过(表2)仿真结果可以看出,本文提出的制导方法能够完成弹道导弹变换打击目标的闭路制导任务,并且精度较高。

表2 变换目标的仿真结果Table 2 Simulation results of changing target
4 结束语
根据弹道导弹的作战特点,提出了弹道导弹主动段变换打击目标的概念,并通过基于空间网格离散的闭路制导方法进行了实现。在制导方法研究中对确定主动段的位置、速度的范围,实时的可攻击范围,需要速度准确计算和实时计算等进行了研究。仿真表明,本文提出的制导方法能够满足导弹变换打击目标的需求,制导精度相对较高,这对于导弹的作战应用和研究发展具有积极的意义。
为了减少运算量,在位置和速度的空间离散时,取的粒度较大,接下来还可以对离散的粒度进行深入的仿真分析,确定合适的粒度,减小制导偏差。在计算需要速度时,令速度分量vy保持不变,在后续研究中,可以令速度倾角ϑ保持不变[15],或给定导弹飞行时间tm,研究在此情况下导弹需要速度的变化规律。
[1] 张毅,肖龙旭,王顺宏.弹道导弹弹道学[M].长沙:国防科技大学出版社,2005. ZHANG Yi,XIAO Long-xu,WANG Shun-hong.Ballistics of Ballistic Missile[M].Changsha:National University of Defense Technology Press,2005.
[2] 鲜勇,田海鹏,雷刚,等.中段智能机动突防后的虚拟标修正研究[J].现代防御技术,2014,42(5):49-54. XIAN Yong,TIAN Hai-peng,LEI Gang,et al.Research on Correction of Virtual Target after Intelligent Maneuvering Penetration in the Middle[J].Modern Defence technology,2014,42(5):49-54.
[3] WANG Fang,LIU Xin-xue,FANG Xi-long,et al.Space-Grid Method in Missile Guidance and Control[J].Journal of Procedia Engineering,2011,15(2):757-767.
[4] 王继平,王明海,杨建明.一种新的闭路制导导引方法[J].航天控制,2007,25(5):58-61. WANG Ji-ping,WANG Ming-hai,YANG Jian-ming.A New Guided Method of Closed-Loop Guidance[J].Aerospace Control,2007,25(5):58-61.
[5] 赵江,周锐.基于倾侧角反馈控制的预测校正再入制导方法[J].兵工学报,2015,36(5):823-830. ZHAO Jiang,ZHOU Rui.Predictor-Corrector Reentry Guidance Based on Feedback Bank Angle Control[J].Acta Armammentaeii,2015,36(5):823-830.
[6] 龙乐豪.总体设计[M].北京:中国宇航出版社,2009. LONG Le-hao.General Design[M].Beijing:China Astronautic Publishing House,2009.
[7] 钱山.弹道导弹变点机动射击诸元快速计算方法研究[D].长沙:国防科技大学,2006. QIAN Shan.The Research of Efficient Method for Firing Data Calculation of Ballistic Missiles in Mobile Condition[D].Changsha:National University of Defense Technology Press,2006.
[8] 高洪月.弹道导弹的导弹设计与仿真[D].哈尔滨:哈尔滨工业大学,2010. GAO Hong-yue.Trajectory Simulation and Design of the Ballistic Missile[D].Harbin:Harbin Institute of Technology,2010.
[9] SHEN Z J,LU P.Onboard Generation of Three-Dimensional Constrained Entry Trajectories[J].Journal of Guidance,Control,an Dynamics,2003,26(1):111-121.
[10] 聂川义,郭建国,周军.空射弹道导弹助推段弹道设计与优化[J].飞行力学,2012,30(4):357-361. NIE Chuan-yi,GUO Jian-guo,ZHOU Jun.Design and Optimization of Boost Phase Trajectory for Air-Launched Ballistic Missile[J].Flight Dynamics,2012,30(4):357-361.
[11] 李喻,杨志红,崔乃刚.助推-滑翔导弹弹道优化研究[J].宇航学报,2008,29(1):66-71. LI Yu,YANG Zhi-hong,CUI Nai-gang.A Study of Optimal Trajectory for Boost-Glide Missile[J].Journal of Astronautics,2008,29(1):69-71.
[12] TAKEHIRA T.Analytical Solution of Missile Terminal Guidance[J].Journal of Guidance Control and Dynamics,1998,21(2):342-348.
[13] 熊介.椭球大地测量学[M].北京:解放军出版社,1988. XIONG Jie.Ellipsoid Geodesy[M].Beijing:PLA Press,1988.
[14] 邓建中,刘之行.计算方法[M].西安:西安交通大学出版社,2000. DENG Jian-zhong,LIU Zhi-xing.Computing Method[M].Xi’an:Xi’an Jiaotong University Press,2000.
[15] 肖龙旭,王继平,魏诗卉,等.一种地地导弹变射面飞行程序设计方法[J].弹道学报,2015,27(2):7-13. XIAO Long-xu,WANG Ji-ping,WEI Shi-hui,et al.A Design Method of Changeable Launching Plane Flight-Process of Ground-to-Ground Ballistic Missile[J].Journal of Ballistics,2015,27(2):7-13.
Closed-Loop Guidance Method of Ballistic Missile for Changing Attacking Target During Boost Phase
FAN Jin-long,LIU Xin-xue,WU Jian,XIA Wei
(The Rocket Force University of Engineering,Primary Command College,Shaanxi Xi’an 710025,China)
An idea of ballistic missile changing attacking target in boost phase is suggested. In order to achieve the guidance purpose for ballistic missile to change an attacking target, a closed loop guidance method based on discrete grid is proposed. The second stage and the dynamical attack zone can be discretized by grid, and the node interpolation parameters are stored on the missile. When the missile changes attacking target in boost phase, the on-board computer calculates the required velocity for closed loop guidance by interpolation method. The simulation results show that the closed-loop method is effective in controlling ballistic missile to change attacking target, and the high accuracy is achieved.
ballistic missile;boost phase;change objectives;space discrete;interpolation solution;required velocity;closed-circuit guidance
2016-06-21;
2016-08-30
范金龙(1990-),男,山东安丘人。硕士生,主要研究方向为飞行器总体、结构分析与飞行力学。
通信地址:102206 北京市昌平区回龙观七里渠南村国发兴宇超市南大院 E-mail:1340081949@qq.com
10.3969/j.issn.1009-086x.2017.03.010
TJ761.3;TJ765.5;TP391.9
A
1009-086X(2017)-03-0061-07
