Cohen-Sutherland直线剪裁算法改进

李竹林

(延安大学 计算机学院，陕西 延安 716000)

Cohen-Sutherland直线剪裁算法改进

李竹林

(延安大学 计算机学院，陕西 延安 716000)

对直线段进行裁剪是计算机图形学需要解决的最基本问题之一，直线段的裁剪速度直接影响到整个图形的裁剪效率。Cohen-Sutherland直线段裁剪算法因分类的不彻底和计算了直线与窗口边延长线上的交点而降低了算法的效率。提出了一种改进Cohen-Sutherland裁剪算法，其基本思想是根据裁剪窗口顶点与直线的位置关系对直线的分类条件进行改进，引入一条从待剪裁直线的端点距窗口最近顶点的辅助线，计算出引入的辅助线与待裁剪直线的夹角，根据夹角的大小，判断出直线究竟与窗口的哪条边相交，从而使求交点次数降低为最高2次。改进后的算法不仅思想简单直观、易实现、效率高，而且对图形裁剪算法的理论研究与应用均有很高的价值。

Cohen-Sutherland；直线裁剪算法；辅助线；夹角计算

0 引 言

直线段裁剪是计算机图形学中一个非常重要的知识点，是二维及三维图形剪裁的基础。从60年代开始到目前为止，广泛使用的三种经典直线裁剪算法是Cohen-Sutherland裁剪算法、中点分割算法以及Liang-Barsky参数裁剪算法[1-4]。其中，Cohen-Sutherland裁剪算法是最早开发的快速线段裁剪算法，得到了高度关注与广泛应用[5-6]。该算法是一种基于区域编码的方法，直线的每个端点均赋予四位二进的区域码，快速判断该条线段是完全在裁剪窗口之内还是窗口之外，或直线的部分在窗口内部分在窗口外，并且能判断出直线可能与窗口的哪条边相交，从而提高了算法效率[1-2]。为了进一步提高Cohen-Sutherland裁剪算法的效率，提出了多种改进方法[7-14]。

在文献[13-14]的基础上，提出了一种更高效的新方法。该算法思路简单直观、易实现，对图形裁剪算法的理论研究与应用都有很高的参考价值。

1 Cohen-Sutherland裁剪原算法

Cohen-Sutherland裁剪算法是利用矩形裁剪窗口的四条边把二维平面分成9个区域，用4位二进制编码CtCbCrCl进行标记，如图1所示。算法的基本思想：待裁剪的直线段两端的编码分别记为code1和code2，与窗口的关系有三种情况：

(1)当code1=code2=0时，完全可见，取之。

(2)当code1&code2≠0时(&为位与运算)，完全不可见，弃之。

(3)当不满足“取”或“弃”的条件，则在与窗口边界的交点处把线段分为两段，其中一段完全在窗口外，弃之；然后对另一段重复上述处理。

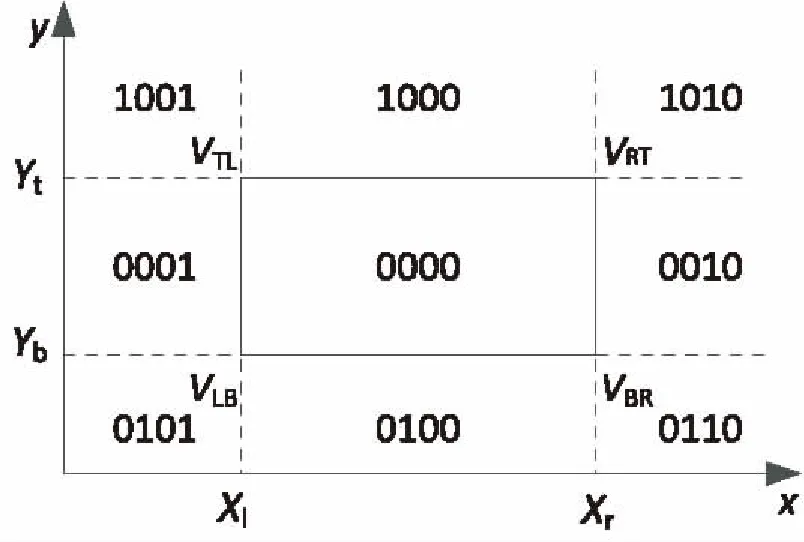
图1 窗口编码区域

Cohen-Sutherland裁剪算法的优点是：第一种情况和第二种情况不需要求交运算；在第三种情况下，为了减少运算量，进行如下处理。首先求交前先判断与窗口哪条边所在直线有交点。判断规则是线段端点编码CtCbCrCl中哪位上的值为“1”，则直线与窗口对应的那条边有交点，需要求此交点；反之，对应边上没有交点。如图2中的直线P1P2，P1的编码是1000，说明与窗口的上边有交点；P2的编码是0100，说明与窗口的下边有交点。

图2 求交直线与窗口的关系图

但是，Cohen-Sutherland原裁剪算法存在以下两个缺点：

(1)不能将所有的完全在窗口外的直线全部判断出来。根据原算法，当code1&code2≠0，并没有将所有的在窗口之外的直线段都判断出来，比如图2中的直线段P3P4，有code1&code2=0。因此，直线与窗口边要做2次求交运算。而实际上，该直线段完全在窗口之外，所有的求交运算没有任何意义。

(2)扩大了直线与窗口边的求交次数。在第三种情种下，所求交点可能有：1个、2个、3个或4个。比如图2中的直线P5P6与窗口的四条边的交点分别为A、B、C、D。而实际上，P5P6只与窗口的上边和右边相交，只需2次求交运算；再如P1P2,实际上与窗口边只有1个交点，而根据原算法，也要进行2次求交运算。实际上，没必要求交的点都是发生在边的延长线上，不妨记为虚交点，可以看出虚交点的求交运算和裁剪过程是没有任何实际意义的。

综合上述问题，可以看出算法的时间复杂度正是由这些不能完全判断和求虚交点的运算以及多出来的裁剪过程带来的。针对这些问题，提出了一种改进的基于直线夹角计算的Cohen-Sutherland裁剪算法，不仅避免了求虚交点的过程，而且大大提高了裁剪算法的效率。

2 改进的Cohen-Sutherland裁剪算法

对原算法的改进是从两方面进行的，首先是对分类条件，然后对直线与窗口是否有交点，在增加辅助线的基础上,提出一种计算直线间夹角的新判断方法。

2.1 分类条件的进一步约束

原算法对完全在窗口之外的判断条件为：当code1&code2≠0时，完全不可见。

如图2所示的直线P3P4、P7P8完全在窗口外，却不能满足code1&code2≠0，可见，原算法给的是充分不必要条件。在原有的基础上，进一步增加约束条件。

改进的基本思想是根据直线与窗口的位置，对第二种(直线完全在窗口外)、第三种(直线与窗口有交点)情况重新作分类判断，并做一些约定：

约定：T(Top)、L(Left)、B(Bottom)、R(Right)分别表示裁剪窗口的上边、左边、下边及右边；记窗口的顶点Vij,即VTL、VLB、VBR、VRT，分别表示左上、左下、右下、右上顶点；待裁剪直线L与窗口的位置关系记为Sij,即STL、SLB、SBR、SRT。Sij取值通过式(1)计算。

设直线L的方程为f(x,y)=Ax+By+C，将窗口的顶点Vij(x,y)代入直线方程，计算得到:

Sij=Ax+By+C

(1)

对于同一条直线，若存在四个顶点Sij同时大于等于零，或者Sij同时小于等于零，记Sij为同号，否则为异号。这样，分类条件则修改为：

第一种情况：当code1=code2=0时，则直线完全可见，“取”之；

第二种情况：当code1&code2≠0且Sij为同号时，则直线完全不可见，“弃”之；

第三种情况：当不满足“取”或“弃”的条件时，直线与窗口有交点，需要求交运算，进行裁剪。

2.2 基于直线夹角计算的求交运算降低法

经过2.1节的分类条件改进，完全在窗口内和完全在窗口外的直线均能全部判断出来，因此本节只针对2.1节中对直线与窗口有交点且扩大了求交次数的情况进行讨论并提出改进措施。

2.2.1 算法改进的基本思路

从2.1节知，原算法只所以存在虚求交次数的可能，是因为不仅求解了直线与窗口的实边相的交点，而且还求解了直线与窗口的延长线的交点。因此，要降低求交次数，必须能判断出直线究竟与窗口的哪些实边有交点，从而避免求直线与窗口边的延长线的交点运算。

经过总结归纳，可得出如图3所示的三种情况，即直线的一个端点一定落在四位编码中有两位同时不等于零的角区域(如图3中的阴影区，在文中任选了左上角1001区域)，而另一端有如下三种情况：

(1)另一端也落在角区域，如直线P1P2。该种情况下，原算法也不能解决直线究竟与窗口的哪条边有实际交点，需要改进。

(2)另一端也落在完全可见区，即编码为0000区域，如直线P5P6。此时从这个端点的编码判断，与窗口的边只有一个相交点，且不是虚点，用原算法即可。

(3)另一端落在既非完全可见区，也非角区域，如直线P3P4。该种情况，从这个端点的编码判断，与窗口的边没有交点，因此用原算法即可。

图3 直线与窗口的延长边相交情况

根据上面三种情况的分析，得出如下事实：只要解决了端点落在角区域时，与窗口的哪条边而非延长线上有交点，则问题得以解决。

2.2.2 基于直线间夹角计算的算法改进

以左上角(1001)区域为例，如图4所示。直线为P0P1，现将左上角区域的直线端点P0与窗口的左上角顶点VTL连接起来，形成一条辅助线P0VTL，这样就形成一个夹角θ(-π/2<θ<π/2)。

图4 直线与辅助线间的夹角图

现在计算θ的大小。设直线P0P1的斜率为k1，辅助线P1VTL的斜率为k2，计算夹角θ的表达式为：

tanθ=(k2-k1)/(1+k1k2)

(2)

(1)左上角(1001)区域。当tanθ>0时，直线P0P1与窗口的左边相交，如图4所示；若当tanθ<0时，直线P0P1与窗口的下边相交；若tanθ=0，则说明直线经过窗口的对角线，从直线的该端点考察，与窗口只有一个交点，且为VTL。

(2)右上角(1010)区域。当tanθ>0时，直线P0P1与窗口的上边相交；当tanθ<0时，直P0P1与窗口的右边相交；当tanθ=0，直线经过窗口的对角线，从直线的该端点考察，与窗口只有一个交点，且为VRT。

(3)右下角(0110)区域。当tanθ>0时，直线P0P1与窗口的右边相交；当tanθ<0时，直线P0P1与窗口的下边相交；当tanθ=0，直线经过窗口的对角线，从直线的该端点考察，与窗口只有一个交点，且为VBR。

(4)左下角(0101)区域。当tanθ>0时，直线P0P1与窗口的下边相交；当tanθ<0时，直线P0P1与窗口的左边相交；tanθ=0，直线经过窗口的对角线，从直线的该端点考察，与窗口只有一个交点，且为VLB。

为了帮助说明问题，将上面的推导进行整理，如表1所示。

表1 直线与窗口边相交判断表

2.3 算法步骤

改进后的算法步骤如下：

Step1:先计算待裁剪直线的两个端点区域编码；

Step2:根据2.1中改进的分类条件判断直线属于哪类，若属于第一、二类转Step6，否则继续；

Step3:若直线的端点没有落在角区域内，则按原算法进行判断、裁剪，否则继续；

Step4:根据2.2节中的方法，作辅助线，并计算直线间夹角的正切值；

Step5:根据表1，判断直线究竟与窗口的哪条边有交点，然后求交运算并裁剪；

Step6:算法结束。

3 算法验证与分析

3.1 算法实例验证

设有裁剪窗口：VTL(4,6)、VRT(12,6)、VBR(12,2)、VLB(4,2)，直线：M(13,10)、N(0,1)。

从落在右上角(1010)区域的端点M考察，经计算得斜率k1=0.69,k2=4.0,tanθ=0.88。根据表现，直线MN应该和窗口的上边相交。同理，考察直线MN的另一个在左下角(0101)区域的端点N，可计算出tanθ=-0.377。根据表1，直线与窗口的左边相交。这样，就得知直线与窗口的上边和左边相交，只需求2个交点，避免了与窗口的右边、下边的延长线求虚交点，从而提高了算法效率。

3.2 算法比较分析

3.2.1 算法改进分析

(1)对分类条件的改进分析[10]。

设在M条直线属于表1中的第二类情况，即完全不可见。其中有N(M≥N)条直线用原算法不能判断，但用改进算法可以。

原算法：对N条直线，可能需要求交2次、3次或4次，在这里不妨记作n次。这N条直线的操作包括n×N次求交运算、n×N次编码运算、n×N次的判断。因此，共需要3n×N次线性运算。

改进算法：对M条直线，符号计算需要4M次线性运算。

(2)降低求交次数的改进分析。

设有M条直线，至少直线的一个端点落在角区域，即code∈{1001,1010,0101,0110}。

原算法：设求交次数为n(n=2,3或4),求交需要n×M次线性运算,编码需要n×M次，判断需要n×M次，总计3n×M次运算。

改进算法：求两条直线的斜率k1、k2及两直线之间的夹角tanθ，然后根据表1判断的结果，做h次求交运算(h=1或2)，总计3M+h×M=(3+h)×M次运算。要使算法改进有意义，只要满足(3+h)×M<3n×M，即h<3(n-1)。根据n的取值范围，当n=2时，3(n-1)=3值最小。显然h的取值足够满足该条件。而事实上，当n=4时，3(n-1)=9，h的取值与之相比小多了。可见算法的改进有较大意义。

3.2.2 算法比较

文献[13-14]是文中提出的Cohen-Sutherland直线裁剪算法的改进方法，也是将求交运算从4次或3次降低为2次。文中改进算法与它们比较，除了消除扩张的虚求交次数外，还具有以下优点：

(1)与文献[13]相比，复杂度降低了。虽然也引入了辅助线，但不需要再分区再编码，明显降低了算法的复杂度。

(2)与文献[14]相比，算法更简洁、直观。文中没有引入复杂的计算与判断，只借助了一条辅助线，使得改进算法直观明了、简单易行。

4 结束语

为了解决Cohen-Sutherland原算法中存在的分类不彻底和求交点次数过高的缺点，提出了一种基于直线夹角计算与判断的Cohen-Sutherland直线段裁剪算法的改进方法，避免了求直线与窗口延长线的交点，将求交点次数降低到最高2次。算法简洁、直观、高效，且易于实现。与原算法及一些相关算法改进的文献相比，大大提高了效率，但是以除法和浮点运算为代价。

[1] 孙家广.计算机图形学[M].第3版.北京:清华大学出版社,2005.

[2] Hearn D, Baker M P, Carithers W.Computer graphics with OpenGL[M].4th ed.[s.l.]:Prentice Hall,2010.

[3] 陆国栋,吴烜晖.基于变窗口过滤技术的线段裁剪中点分割算法[J].计算机辅助设计与图形学学报,2002,14(6):513-517.

[4] Peng H， Lu Guodong， Tan J R.A new algorithm of polygon clipping against rectangular window based on the endpoint and intersection-point encoding[J].Journal of Engineering Graphics,2006,27(4):72-76.

[5] 熊忠阳，杨营辉，张玉芳.基于密度的kNN分类器训练样本裁剪方法的改进[J].计算机应用，2010，30(3)：799-801.

[6] Guid N,Kolmanic S.A new approach in CAD system for design shoes[J].Journal of Computing and Information Technology，2003,11(4):319-326.

[7] Qatawneh M，Sleit A，Almobaideen W.Parallel implementation of polygon clipping using transputer[J].American Journal of Applied Sciences,2009,6(2):214-218.

[8] Ray B K.A line segment clipping algorithm in 2D[J].International Journal of Computer Graphics,2012,3(2):51-76.

[9] 熊中敏，李宏伟，马春光.二维线段裁剪新算法[J].哈尔滨理工大学学报，2001，6(2):7-10.

[10] 孔德慧，尹宝才，刘媛媛.对Cohen-Sutherland线段裁剪算法的改进[J].北京工业大学学报，2002,28(4):483-486.

[11] 黄初华，陈孝威.对Cohen-Sutherland裁剪算法的改进[J].贵州大学学报:自然科学版，2008，25(3):268-271.

[12] 王慧玲，冯雪花.对Cohen-sutherland线段裁剪算法的分析及改进[J].伊犁师范学院学报:自然科学版，2008(4):38-41.

[13] 李竹林，雷 岗.一种改进的Sutherland-Cohen 裁剪算法[J].计算机工程与应用，2012，48(34)：175-178.

[14] 李竹林,张根耀,郭万鑫.基于符号判断的C-S直线裁剪算法改进[J].微电子学与计算机,2015,32(8):150-153.

Modification of Cohen-Sutherland Line Clipping Algorithm

LI Zhu-lin

(Institute of Computer Science,Yan’an University,Yan’an 716000,China)

Line segment clipping is one of the most basic problems to be solved in computer graphics,and the clipping speed directly affects the clipping efficiency of the whole graph.Cohen-Sutherland line segment clipping algorithm has lower efficiency because line segment classification is not complete and the intersection points are still calculated between straight line and the window extension edge.A modified Cohen-Sutherland line clipping algorithm based on linear angle calculation has been proposed.It is the idea that the line classification conditions can be improved using sign relations of four windows vertex and line,then if an auxiliary line from the end of the line to be cut to the nearest vertex of the window is made,the angle between an auxiliary line and a line to be cut can be calculated,and the intersecting window edge is determined according to the sign of angle.This method reduces the number of intersection.The modified algorithm not only simple and intuitive,easy to implement and of high efficiency,but also valuable for theory research and application of clipping technology.

Cohen-Sutherland;line segment clipping algorithm;auxiliary line;angle calculation

2016-05-20

2016-08-24 网络出版时间：2017-04-28

国家自然科学基金资助项目(11471007);延安市重大科技攻关项目(2014CGZH-13);国家大学生创新训练项目(1498)

李竹林(1972-)，女，博士，副教授，研究方向为图形图像处理。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170428.1702.012.html

TP301.6

A

1673-629X(2017)06-0032-04

10.3969/j.issn.1673-629X.2017.06.007