基于拟合优度检验-贝叶斯理论的生态混凝土碳化深度概率模型研究
2017-06-26吴柳董峰辉
吴柳,董峰辉
(1.东莞市交业工程质量检测中心,广东东莞523125;2.同济大学土木工程学院,上海市200092)
基于拟合优度检验-贝叶斯理论的生态混凝土碳化深度概率模型研究
吴柳1,董峰辉2
(1.东莞市交业工程质量检测中心,广东东莞523125;2.同济大学土木工程学院,上海市200092)
针对生态混凝土碳化深度具有随机性的特点,提出基于拟合优度检验和贝叶斯理论相结合的方法进行生态混凝土碳化深度概率模型分析。采用拟合优度检验识别生态混凝土碳化服从的最优概率分布类型,采用贝叶斯理论对最优概率分布类型中的参数进行估计,在此基础上进行碳化可靠度分析。通过3组检测数据来说明基于拟合优度检验和贝叶斯理论相结合的方法在生态混凝土碳化深度概率模型研究和碳化可靠度分析中的应用过程。结果表明:与传统方法相比,基于拟合优度检验和贝叶斯理论相结合的方法进行生态混凝土碳化深度概率模型和碳化可靠度分析更加符合工程实际,便于工程应用。
生态混凝土;碳化深度;概率模型;拟合优度检验;贝叶斯理论
0 引言
生态型混凝土即能够适应生物生长,对调节生态平衡、美化环境景观、实现人类与自然的协调具有积极作用的混凝土材料[1]。生态混凝土是一种具有较大孔隙率的透水性混凝土,在自然条件下,护堤植生的生态混凝土因经常遭受干湿、冷热、冻融交替、环境水质和大气污染等综合作用而易降低寿命,其中由环境导致的碳化是造成钢筋混凝土结构耐久性损伤的主要原因之一。由于生态混凝土本身的变异性和结构所处环境的不确定性,使得生态混凝土的碳化具有很大的不确定性。本文通过用现场浇筑的生态混凝土试块在实验室快速碳化箱里进行的快速碳化试验,对生态混凝土碳化深度进行统计分析,从而建立起生态混凝土碳化的概率模型,为生态混凝土结构的耐久性分析和寿命预测提供依据。
已有的混凝土碳化深度概率模型研究都是基于当前检测数据样本(样本量足够大,不适合小样本),没有充分利用已有混凝土碳化深度概率模型的有效信息,因此不能够准确反映混凝土碳化的概率本质[2]。此外,已有的混凝土碳化深度概率模型均是事先假定概率分布类型[3-8],然后对概率分布类型中的参数进行估计,因此混凝土碳化深度概率模型的正确性依赖于事先假定的概率模型,如果假定模型不正确,则参数估计就没有意义。本文基于拟合优度检验和贝叶斯理论相结合的方法针对生态混凝土碳化深度概率模型进行研究。首先基于拟合优度检验识别出生态混凝土碳化深度服从的最优概率分布类型,然后采用贝叶斯理论进行参数估计,这样既能有效地利用样本的先验信息,又能依据当前样本值(适合小样本),因此,所得到的碳化深度概率分布模型分析结果具有很好的工程应用价值。
2 拟合优度检验[9,10]
根据已有统计资料表明,混凝土碳化深度大致服从正态分布、对数正态分布和极值I型分布,运用χ2检验法对生态混凝土碳化深度x统计分布进行拟合性检验。
2.1χ2检验法
χ2检验法是将来自母体的一组容量为n的子样,根据子样值的范围,把它划分成m个区间,并且每个区间的个数不少于5个。如果记vk为第k个区间内子样频数,pk是按假设H0确定的分布F(x)计算的概率,那么统计量将反映假设分布F(x)与实际分布的总偏差。皮尔逊已经证明,当n→∞时,不论F(x)的形式如何,D的分布都将趋于服从参数为m-r-1的χ2分布,其中r是分布F(x)中用子样估计的参数个数。取检验的显著性水平为α,若D<χ2α,则接受假设H0,若D>χ2α,则拒绝假设H0。
2.2 正态分布检验
假设x服从正态分布,即建立假设H0:
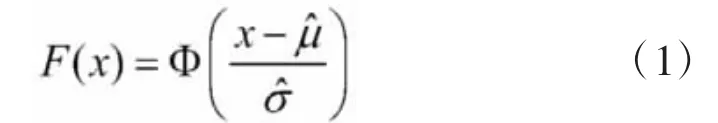
2.3 对数正态分布检验
假设x服从对数正态分布,即建立假设H0:
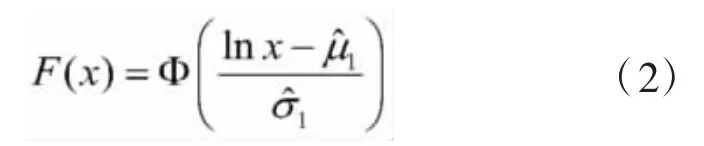
2.4 极值I型分布检验
假设x服从极值I型分布,即建立假设H0:
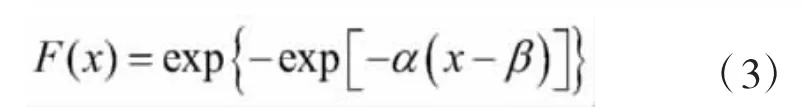
其中参数α、β的估计值分别为:
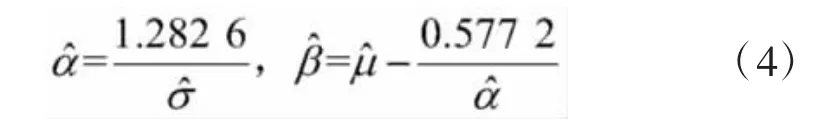
3 贝叶斯理论[10-12]
贝叶斯方法的基本思路是:若基于已有预测模型确定的样本分布中某一状态参数的先验概率分布与基于实际检测数据而确定的该状态参数的条件后验概率分布一致,则可依据后验分布概率密度对先验分布的相关参数重新进行估计和检验。由于基于贝叶斯方法的预测结果平衡了主观先验样本信息和客观后验检测样本信息,这样能使预测结果的准确性和客观性得到有效提高。
推广贝叶斯法是根据贝叶斯统计理论引申而来,利用先验概率分布信息,即利用已积累混凝土碳化深度参数的试验资料,对分布概型进行初估,再根据后验信息,即某一具体混凝土碳化深度的有限试验数据,对概率分布参数重新加以估计。如此能较好地避免由于试验数量不足引起的统计参数的偏差,并确定生态混凝土碳化深度的概率分布参数。
设随机变量的先验分布密度为f'(θ),后验分布密度为f"(θ),根据贝叶斯公式,有:
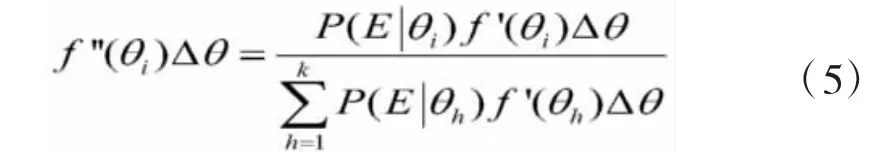
由于贝叶斯统计中假定先验分布与后验分布概型一致,θ的后验分布参数可近似确定:
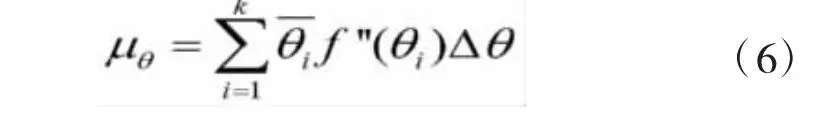
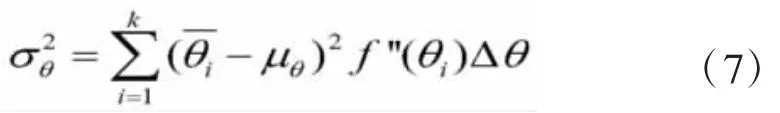
4 概率模型研究及可靠度分析步骤
基于上述拟合优度检验和贝叶斯理论,可得生态混凝土碳化深度概率模型研究及可靠度分析步骤如下:
(1)对生态混凝土碳化深度进行样本采集;(2)基于拟合优度检验来识别生态混凝土碳化服从的最优概率分布类型;(3)采用贝叶斯理论来估计概率分布类型中的参数;(4)确定生态混凝土碳化允许目标值,建立碳化极限状态方程;(5)计算生态混凝土碳化可靠度指标。
5 实例分析
5.1 原材料
水泥:镇江京阳嘉新P·O42.5R(普通硅酸盐水泥)。砂:江砂。添加剂:由日本亚洲产业株式会社开发研制的生态混凝土添加剂S R-3[13],密度为1.044 g/m L,它是一种以碳酸钙、硅石粉为主要成分的橘黄色无机质悬浮液。碎石:5~16 mm的连续级配。
5.2 试件尺寸和配合比
碳化试件的尺寸为150mm×150mm×150mm。试件配方见表1。

表1 碳化试验中生态混凝土的配方
5.3 试件制作
在生态混凝土浇筑工地现场制作4组碳化试件,每组3块,进行碳化后的深度测定。混凝土搅拌完毕后立即装入试模浇制试件,用人工成型,分两层装入试模,每层用金属棒插捣11下,然后将试件自然养护3 d后,在(20±3)℃的水中浸泡4 d。
5.4 试验方案
将4组试件中的3组放入快速碳化箱中进行碳化试验[14]。试验按照《普通混凝土长期性能和耐久性试验方法》(G B J 82—85)进行,碳化时间为28 d。快速碳化箱具有自动调控温度、湿度及C O2体积分数的功能,碳化箱中碳化环境设置为:C O2体积分数为(20±3)%,相对湿度为(70±5)%,温度为(20±5)℃。分别测试3组试件C-1,C-2,C-3的14,28 d碳化深度。
5.5 试验结果
碳化深度的测定结果见表2。
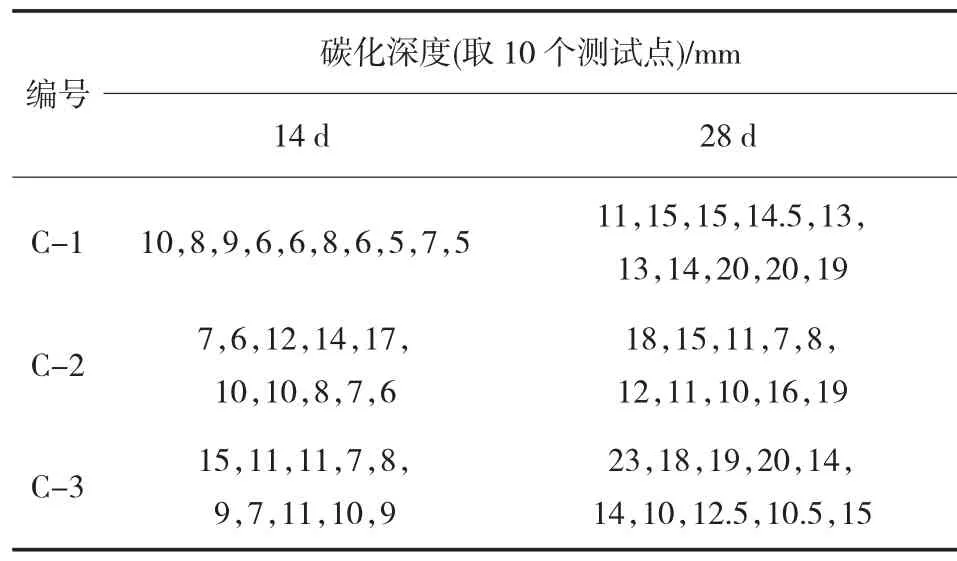
表2 立方体试件的碳化深度
5.6 碳化深度概率模型分析
根据传统生态混凝土碳化深度概率模型预测方法,均假设碳化深度服从正态分布,然后采用最大似然估计法进行参数估计。根据本文提出的方法,首先采用拟合优度检验来识别生态混凝土碳化深度服从哪种概率分布,然后依据贝叶斯理论对分布参数进行估计。采用传统最大似然估计法和本文提出的基于拟合优度检验和贝叶斯理论的方法对生态混凝土的碳化深度进行概率模型预测,结果见表3。
根据拟合优度检验结果,如按常规的χ2检验法,编号C-1生态混凝土14 d碳化深度和编号C-3生态混凝土28 d碳化深度接受对数正态分布,编号C-1生态混凝土28 d碳化深度接受极值I型分布,其余编号生态混凝土碳化深度服从正态分布。造成这种现象的原因是样本容量的不足,而在实践中样本容量总是有限的。此外,即便采用优度拟合检验,编号C-2生态混凝土14 d碳化深度,编号C-3生态混凝土14 d碳化深度和编号C-2生态混凝土28 d碳化深度均接受正态分布,但是由于试验中样本数量的不足,导致参数的贝叶斯估计结果和最大似然估计结果有差异,均值最大相对误差为标准差最大相对误差为
5.7 碳化可靠度分析
生态混凝土碳化损伤极限状态方程可以表示为:

式中:C为生态混凝土碳化允许指标,X为生态混凝土碳化深度。
关于生态混凝土碳化允许指标的确定目前还没有明确的标准。为了便于分析,本文将生态混凝土碳化允许指标取为25 mm。针对上述检测结果,基于拟合优度检验和贝叶斯理论相结合的方法和最大似然估计法确定的生态混凝土碳化深度,采用J C法计算生态混凝土碳化可靠度指标,结果见表4。
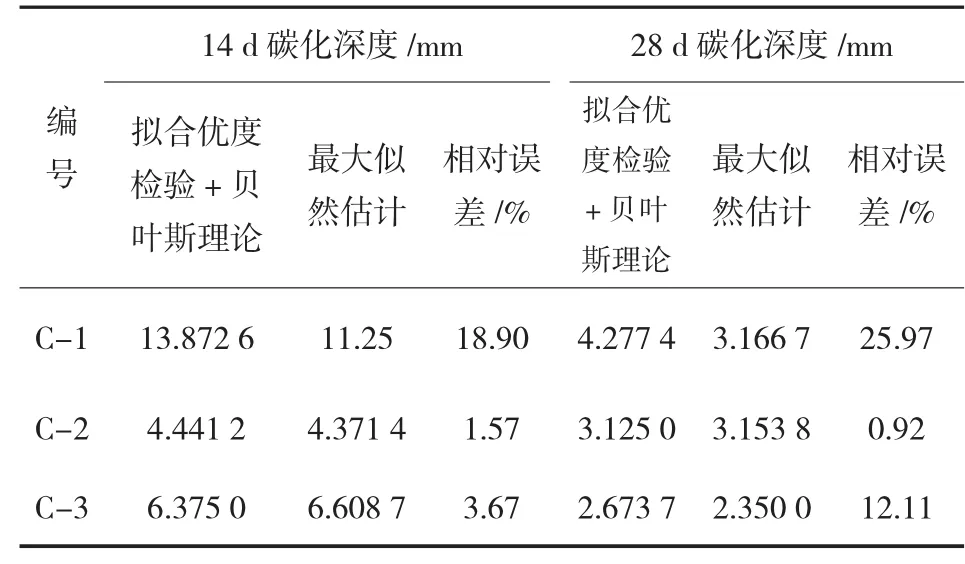
表4 生态混凝土碳化可靠度指标
由表4结果分析可知,编号C-2生态混凝土14 d碳化深度,编号C-3生态混凝土14 d碳化深度和编号C-2生态混凝土28 d碳化深度基于拟合优度检验结果服从正态分布,因此与最大似然估计法计算的生态混凝土碳化可靠度指标误差最大为3.67%。但是,编号C-1生态混凝土14 d碳化深度和编号C-3生态混凝土28 d碳化深度接受对数正态分布,编号C-1生态混凝土28 d碳化深度接受极值I型分布,与最大似然估计法计算的生态混凝土碳化可靠度指标误差分别为18.90%,12.11%和25.97%。造成这一现象的原因是由于样本量的不足导致生态混凝土碳化深度随机变量的概率模型预测偏差较大,误差较大为对数正态分布,误差最大为极值I型分布。
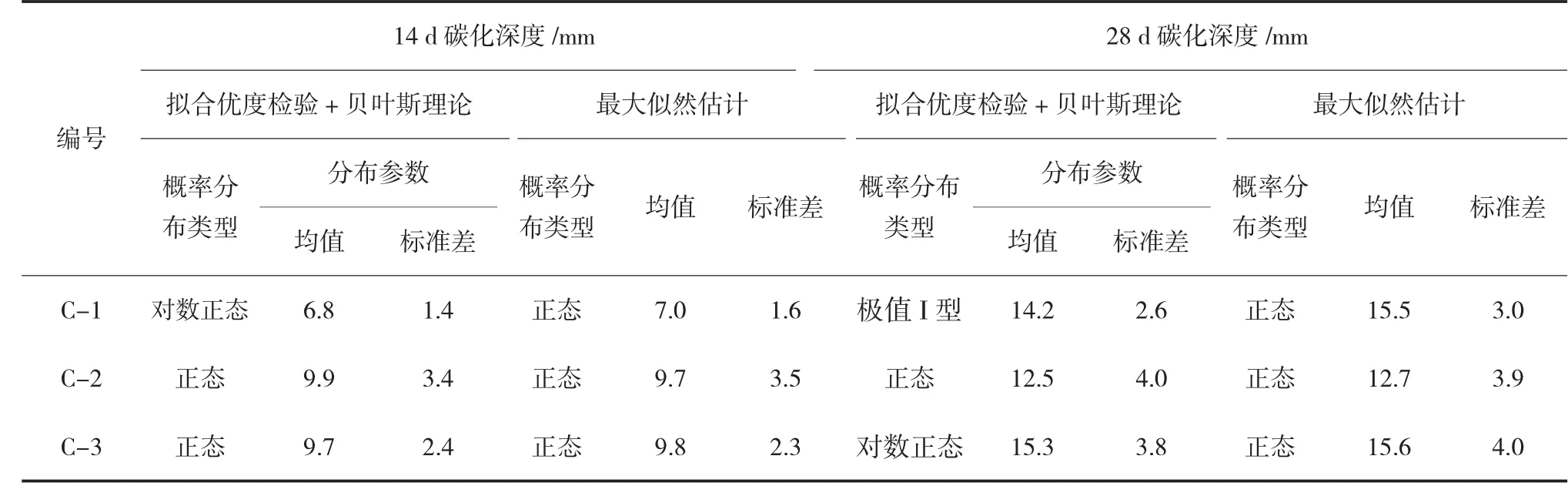
表3 生态混凝土碳化深度概率模型预测结果
6 结语
(1)由于样本量较少,传统最大似然估计法不适合进行生态混凝土碳化深度概率模型分析。
(2)基于拟合优度检验和贝叶斯理论相结合的方法适合对小样本生态混凝土碳化深度进行概率模型分析。
(3)基于拟合优度检验和贝叶斯理论相结合的方法进行生态混凝土碳化深度概率模型和碳化可靠度分析比传统的最大似然估计法更加符合工程实际,便于工程应用。
[1]李湘洲.走向可持续发展的生态混凝土技术[J].中国建材, 2003(1):34-35.
[2]茆诗松.贝叶斯统计[M].北京:中国统计出版社,2012.
[3]金伟良,鄢飞.混凝土碳化指数的概率模型[J].混凝土,2000(1): 35-37.
[4]丁伯阳,郑工钦,孔德玉.概率模型分析与混凝土碳化[J].浙江工业大学学报,2006,34(2):210-212,219.
[5]牛荻涛.混凝土结构耐久性与寿命预测[M].北京:科学出版社, 2003:18-33.
[6]屈文俊,陈道普.混凝土碳化的随机模型[J].同济大学学报(自然科学版),2007,35(5):577-581.
[7]吴本英,周锡武.基于贝叶斯方法的混凝土结构碳化深度预测研究[J].武汉理工大学学报,2011,33(3):103-107.
[8]刘荣桂,陆春华,雷丽恒,等.现代预应力结构耐久性(碳化)模型研究[J].工业建筑,2004,34(4):69-72.
[9]张博庭.有限比较法进行拟合优度检验[J].岩土工程学报,1991,13(6):84-91.
[10]卫军,罗扣.基于贝叶斯方法的时变可靠度分析[J].华中科技大学学报(自然科学版),2007,35(2):1-3.
[11]刘书奎,吴子燕,韩晖,等.基于物理参数贝叶斯更新的桥梁剩余强度估计研究[J].工程力学,2011,28(8):126-132.
[12]宁宝宽,王维纲.浅基础可靠性设计中的贝叶斯统计方法及应用[J].沈阳工业大学学报,2005,27(1):103-106.
[13]亚洲产业株式会社.无机质混合材S R-3配合现场浇筑透水性混凝土.
[14]刘荣桂,万炜,陆春华,等.现浇护堤植生型生态混凝土耐久性的试验研究[J].工业建筑,2005,35(z1):668-672.
T U528.01
A
1009-7716(2017)06-0254-04
10.16799/j.cnki.csdqyfh.2017.06.075
2017-03-16
吴柳(1984-),女,广东东莞人,工程师,从事公路桥梁检测工作。
