对心直动滚子推杆盘形凸轮机构的运动分析

关锋

（山西机电职业技术学院，山西长治046011）

对心直动滚子推杆盘形凸轮机构的运动分析

关锋

（山西机电职业技术学院，山西长治046011）

利用Pro/E软件对心直动滚子推杆盘形凸轮机构进行运动分析，得到了位移、速度和加速度的仿真结果，为后续的机构优化提供了一定的理论基础。

凸轮机构；Pro/E；运动分析

凸轮机构是机械中的一种常用机构，在自动化和半自动化机械中应用非常广泛。凸轮机构由凸轮、从动件和机架3个基本构件组成的一种高副机构。只要能够设计出凸轮轮廓曲线，从动件就可以得到各种预期的运动规律[1]。采用Pro/E软件进行分析，可使设计更加方便，为后续的机构优化提供一定的理论基础。

1 凸轮设计思路

设计者需要确定凸轮的基圆半径，根据从动件推杆的运动规律，能够解算出凸轮理论轮廓曲线的解析方程。然后在Pro/E软件建模环境中输入变量和表达式方程来创建凸轮的理论轮廓曲线。首先输入变量和驱动参数，然后输入计算变量x和y。表达式的形式会随着转角的变化而发生相应的变化。所以，除此以外还必须根据转角的条件，写出相应的凸轮轮廓曲线的数学表达式，最后绘制出它们的图形。

完成数学表达式后，在Pro/E软件建模的环境中选择“插入”中“模型基准”的“曲线”命令，也可以通过单击绘图区右侧的图标，系统会自动弹出“曲线选项”的菜单，选定“从方程”的选项。选择合适的坐标系后，设置t为系统变量，然后用定义的x和y来表示Pro/E系统坐标中的变量，同时把z定义为常量0，得到凸轮理论轮廓曲线。当分别插入不同阶段的理论轮廓曲线之后，通过扫描法可以将理论轮廓曲线可以作为扫描轨迹线，向内作距离为滚子半径的扫描曲面或者偏移曲线，进而得到凸轮的实际轮廓曲线或曲面。最后将凸轮的实际轮廓曲线进行拉伸的操作，拉伸值为凸轮的厚度值，便可以得到凸轮的三维实体模型。

2 凸轮机构实例

某企业需要设计一对心直动滚子推杆盘形凸轮机构。推杆的运动规律为：当凸轮转过90°时，推杆等加速等减速上升15 mm；凸轮继续转过90°时，推杆停止不动；凸轮再继续转过60°时，推杆等加速等减速下降15 mm；凸轮转过余下的120°时，推杆又停止不动。假设凸轮是逆时针方向等速转动的圆周运动，基圆半径是50 mm，推杆滚子半径是10 mm，凸轮的中央孔径为20 mm，厚度为25 mm.

3 凸轮机构的三维模型

当利用Pro/E系统创建由方程描述的各种曲线时，必须将曲线方程的数学表达式转化为Pro/E系统中的相应表达式[2]。根据对心直动滚子推杆盘形凸轮轮廓曲线的数学表达式的情况，通过在Pro/E记事本中可以创建与之所对应的数学表达式。t是从0到1的取值范围。

（1）已知条件，驱动参数为

h=15/*升程，长度，单位为mm

r0=50/*基圆半径，长度，单位为mm

rr=10/*滚子半径，长度，单位为mm

rb=10/*凸轮中央圆孔半径，长度，单位为mm

fai1=90/*推程转角，角度，单位为degree

fai2=90/*远休止角，角度，单位为degree

fai3=60/*回程转角，角度，单位为degree

fai4=120/*近休止角，角度，单位为degree

（2）推程等加速阶段：fai1=90

a1=0/*起始角，角度，单位为degree

b1=fai1/2/*终止角，角度，单位为degree

fai=a1*（1-t）+b1*t/*中间角变量，角度，单位为degree

s1=2*h*fai*fai/（fai1*fai1）/*升程变量，长度，单位为mm

x=（r0+s1）*sin（fai）/*理论轮廓曲线x坐标值，长度，单位为mm

y=（r0+s1）*cos（fai）/*理论轮廓曲线y坐标值，长度，单位为mm

（3）推程等减速阶段：fai1=90

a2=fai1/2/*起始角，角度，单位为degree

b2=fai1/*终止角，角度，单位为degree

fai=a2*（1-t）+b2*t/*中间角变量，角度，单位为degree

je=fai1-fai/*中间角变量，角度，单位为degree

s2=h-2*h*je*je/（fai1*fai1）/*升程变量，长度，单位为mm

x=（r0+s2）*sin（fai）/*理论轮廓曲线x坐标值，长度，单位为mm

y=（r0+s2）*cos（fai）/*理论轮廓曲线y坐标值，长度，单位为mm

（4）远休止阶段：fai2=90

a3=fai1/*起始角，角度，单位为degree

b3=fai1+fai2/*终止角，角度，单位为degree

fai=a3*（1-t）+b3*t/*中间角变量，角度，单位为degree

s3=h/*升程变量，长度，单位为mm

x=（r0+s3）*sin（fai）/*理论轮廓曲线x坐标值，长度，单位为mm

y=（r0+s3）*cos（fai）/*理论轮廓曲线y坐标值，长度，单位为mm

（5）回程等加速阶段：fai3=60

a4=fai1+fai2/*起始角，角度，单位为degree

b4=a4+fai3/2/*终止角，角度，单位为degree

fai=a4*（1-t）+b4*t/*中间角变量，角度，单位为degree

je4=fai-a4/*中间角变量，角度，单位为degree

s4=h-2*h*je4*je4/（fai3*fai3）/*升程变量，长度，单位为mm

x=（r0+s4）*sin（fai）/*理论轮廓曲线x坐标值，长度，单位为mm

y=（r0+s4）*cos（fai）/*理论轮廓曲线y坐标值，长度，单位为mm

（6）回程等减速阶段：fai3=60

a5=fai1+fai2+fai3/2/*起始角，角度，单位为degree

在t2n-3至t2n-1阶段,可以假设信标节点相对静止不动,因此节点B相对于节点A的移动距离即为dAB(t2n-1,t2n-1)-dAB(t2n-3,t2n-3).CB-Sync算法通过1.3节估计的多普勒规模因子η,可求得在t2n-3和t2n-1阶段的平均移动速度

b5=fai1+fai2+fai3/*终止角，角度，单位为degree

fai=a5*（1-t）+b5*t/*中间角变量，角度，单位为degree

je5=fai-fai1-fai2-fai3/*中间角变量，角度，单位为degree

s5=2*h*je5*je5/（fai3*fai3）/*升程变量，长度，单位为mm

x=（r0+s5）*sin（fai）/*理论轮廓曲线x坐标值，长度，单位为mm

y=（r0+s5）*cos（fai）/*理论轮廓曲线y坐标值，长度，单位为mm

（7）近休止阶段：fai4=120

a6=fai1+fai2+fai3/*起始角，角度，单位为degree

fai=a6*（1-t）+b6*t/*中间角变量，角度，单位为degree

s6=0/*升程变量，长度，单位为mm

x=（r0+s6）*sin（fai）/*理论轮廓曲线x坐标值，长度，单位为mm

y=（r0+s6）*cos（fai）/*理论轮廓曲线y坐标值，长度，单位为mm

这一工作一般情况下可以通过选择“插入”中“模型基准”的“曲线”命令来实现。在系统弹出的“曲线选项”菜单中只需选取“从方程”选项，即可以利用输入的曲线方程式精确地创建凸轮理论轮廓曲线如图1所示。依据凸轮曲线构建的凸轮的三维实体模型如图2所示。在此基础上创建机座及从动件，并完成凸轮机构的装配，如图3所示，为凸轮机构的运动分析提供基础。

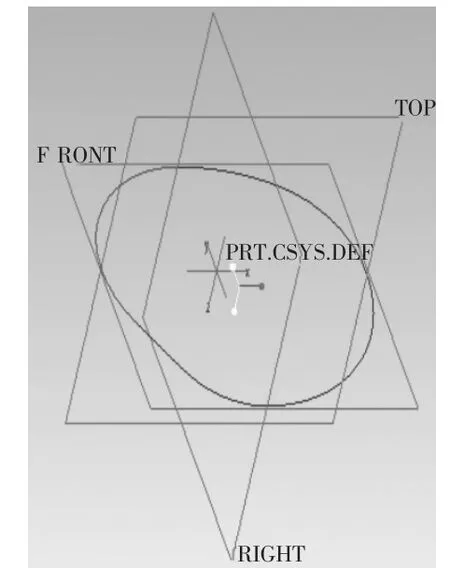
图1 凸轮理论轮廓曲线

图2 凸轮实体模型

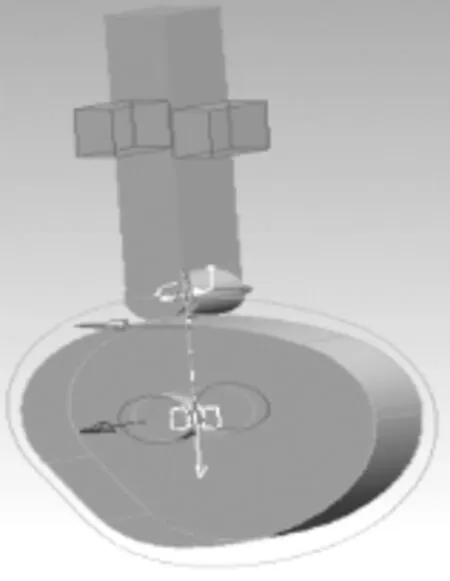
图3 凸轮机构实体模型

3.1 凸轮机构的运动分析

在绘图区右侧单击生成测量结果图标，系统会自动弹出“测量结果”的对话框[3]。单击新建测量图标，弹出“测量定义”对话框，名称默认为measure1，在“类型”选项框中选择“位置”选项，在“点或运动轴”选项框中点击选择图标后选取绘图区连杆上的某一点（如图4所示）作为分析点，在“分量”选项框中选择“Y分量”，完成后“测量定义”对话框如图5所示。按照同样的步骤，测量速度与加速度，设置完成后的“测量定义”速度和加速度对话框如图6和图7所示。最后单击“确定”按钮，出现“测量结果”的对话框，如图8所示。

图4 选取推杆上某一分析点

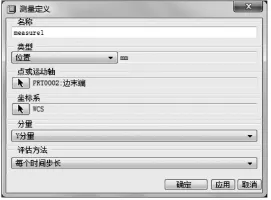
图5 位置类型的对话框

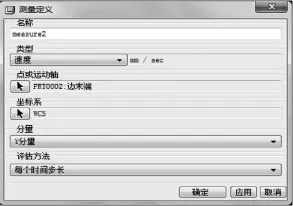
图6 速度类型的对话框

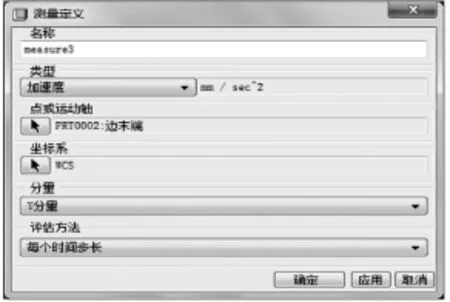
图7 加速度类型的对话框

图8 测量结果的对话框

然后选中所有的分析项，点击动态分析，并勾选“分别绘制测量图形”。点击绘制测量结果图标，就可以绘制出位移、速度和加速度的曲线，如图9所示。

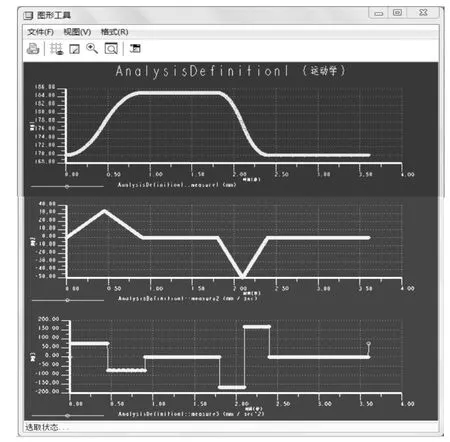
图7 图形工具的对话框

3.2 结果分析

通过凸轮机构的运动分析，非常清楚地看到了凸轮机构的运动情况，同时得到了从动件推杆在运动过程中的位移、速度和加速度曲线[4]。

在运动分析的过程中，凸轮旋转一周的时间为3.6 s，推杆顶部上一点为其测量点。从图7中可以看到，从0 s～0.45 s时（凸轮转过约45°），推杆的位移上升，速度也在上升，加速度不变；从0.45 s～0.9 s时（凸轮又转过约45°），推杆上升至185 mm最高点，与开始位置相比，推杆升程为15 mm（即变化值为170 mm～185 mm），在这个时候速度直线下降，加速度仍然不变，由原来的匀加速变成了匀减速；从0.9 s～1.8 s时（凸轮转过约90°），推杆位移没变化，速度和加速度都为0；从1.8 s～2.4 s时（凸轮转过约60°），推杆位移下降了15mm，速度在1.8 s～2.1 s时间段匀加速，在2.1 s～2.4 s时间段匀减速，两段时间范围内加速度等值反向；从2.4 s～3.6 s（凸轮转过约120°），推杆位移没有变化，速度与加速度都为0.通过分析可知，从动件推杆的运动规律完全能够满足设计的要求。

4 结束语

本文介绍了Pro/E的三维建模和仿真技术，对凸轮机构进行了仿真分析，给后续的机构优化提供了一定的理论基础。

[1]林胜．基于Pro/E软件的凸轮机构虚拟设计与运动仿真[J].轻工科技，2016（5）：63-64.

[2]杨彬彬．基于Pro/E凸轮机构的仿真设计[J].企业技术开发，2011（21）：86-87.

[3]赵仙花，张毅.基于Pro/ENGINEER的凸轮机构的动态分析设计[J].焦作大学学报，2015，（2）：105-107.

[4]周昇，赵灵.基于Pro/E的凸轮的设计和优化[J].机械工

程师，2013（1）：84-86.

Kinematic Analysis of the Cam Mechanism with Straight Moving Roller Follower

GUAN Feng
（Shanxi Institute of Mechanical and Electrical Engineering，Changzhi Shanxi 046011，China）

Taking as an example a set of the cam of the disc cam with the roller follower of the heart，introduces three-dimensional modeling and motion analysis of cam mechanism by using Pro/E graphics software，which verifies the correctness and reliability of the design by analyzing the simulation results of the displacement，velocity and acceleration and it provides a certain theoretical basis for subsequent optimization.

cam mechanism；Pro/E；motion analysis

TP39

A < class="emphasis_bold">文章编号：1

1672-545X（2017）05-0283-04

2017-02-17

关锋（1980-），男，山西长治人，硕士，讲师，主要从事机械设计研究。