非均匀天线组阵中引入对角加载的合成算法*
2017-06-23伍警
伍 警
(中国工程物理研究院 a.电子工程研究所;b.研究生院,四川 绵阳 621999)
非均匀天线组阵中引入对角加载的合成算法*
伍 警**
(中国工程物理研究院 a.电子工程研究所;b.研究生院,四川 绵阳 621999)
针对非均匀天线组阵中常用的SUMPLE与PMFM(Proposed Matrix-Free Method)算法合成性能较差的问题,分别在SUMPLE与PMFM算法模型中引入对角加载技术,提出了一种新的信号合成算法。该算法利用权值幅度估计各路噪声功率,并对角加载到权值迭代算法中以得到准最优复权值向量。理论分析与数值仿真均表明,在不明显增加计算量的基础上,新算法在非均匀组阵中的合成损失明显低于SUMPLE与PMFM算法,同时新算法的收敛速度也与各自模型算法相当,因此更加适用于实际组阵系统,具有重要的工程应用价值。
天线组阵;非均匀组阵;合成算法;对角加载
1 引 言
天线组阵利用分布的不同天线组成阵列,同时接收同一信源信号,并将各路接收信号进行合成,从而提高信号信噪比[1]。天线组阵的优势包括更好的性能、更强的稳健性、更低的建造费用、更灵活的计划安排和对科学界更广泛的支持[2],在深空探测中发挥了重要的作用。
合成系统将各天线输入信号进行加权合成输出高信噪比信号,以便后续进行信号解调与检测。由于各路信号信噪比很低,必须采用信号相关等技术确定各路信号幅度和相位修正复权值[3]。目前常用的信号相关算法有SIMPLE、SUMPLE[4-5]、Eigen[6]等算法,其中SIMPLE算法在信号信噪比较低情况下合成性能较差。而SUMPLE不适合天线数目很少情况下的组阵,同时由于各路参考信号不同,存在相位漂移问题,需要采取各种方法进行补偿。基于最大信噪比(Maximum Signal-to-Noise Ratio,MSNR)准则的Eigen算法利用矩阵特征值分解估计合成权值,在大规模组阵下运算量大且实时性差。为此,文献[7]提出了一种迭代算法——幂法(Power Method,PM);为进一步降低运算量,又提出了无需矩阵计算的幂法算法,即PMFM算法。
以上算法均假设各路噪声功率相等,而在实际组阵中,为充分利用已有天线资源[8-9],阵中各天线型号、地理位置可能存在差异,此时各天线信噪比并不相同,算法合成损失较大。文献[10]将SUMPLE算法推广到非均匀组阵中,利用天线的有效面积和系统噪声温度对权值幅度进行修正,但无法真实反映信号实际质量。文献[11]提出了一种利用合成权值估计各天线信号强度的方法,但仿真结果表明较低信噪比情况下,算法估计性能急剧恶化。而文献[12]在低信噪比情况下对各路信号功率归一化后,假设各噪声功率近似相等,此时SUMPLE算法具有良好的合成性能,但当假设条件不满足时,合成性能变差。另外,文献[13]针对深空天线组阵相关合成算法进行了Simulink仿真与分析,权值幅度通过信噪比统计测量模块估计得到,运算量大,且低信噪比下合成性能较差。
针对各路噪声功率相差较大的非均匀天线组阵中SUMPLE、PMFM算法合成损失较大的问题,本文首先分析了非均匀组阵中SUMPLE、PMFM算法合成性能较差的原因,并提出了引入对角加载技术的合成算法,后续的理论分析与数值结果都验证了本文算法的有效性。
2 信号模型
考虑N副天线对信号进行接收。假设各路信号间的时差、频差已获得同步补偿,第i个阵元接收信号经采样后可表示为
xi(l)=αis(l)e-jθi+ni(l),l=1,2,…,L;i=1,2,…,N。
(1)
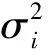
3 非均匀组阵中引入对角加载的合成算法
3.1 现有SUMPLE、PMFM算法性能分析
输入信号与复权值向量定义如下:

(2)
则合成信号为
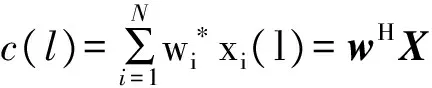
(3)
输出信噪比可表示成
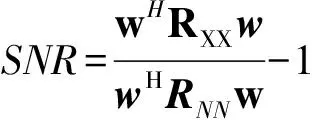
(4)

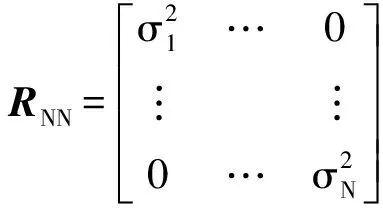
(5)
而SUMPLE与PMFM算法假设各路噪声功率相同,即各路噪声功率估计值为
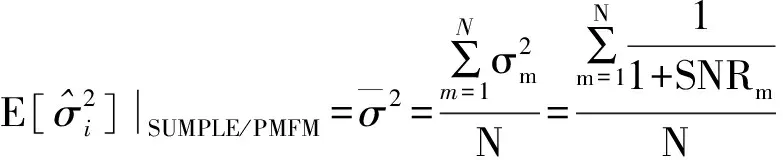
(6)
此时对应的噪声功率归一化偏差为
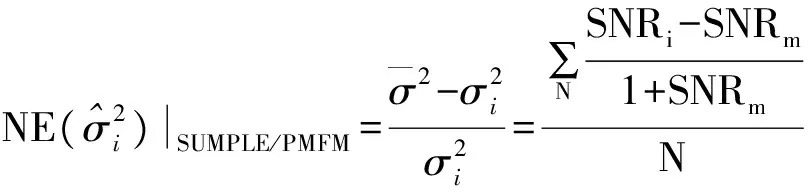
(7)
总归一化偏差为

(8)
式(7)中SUMPLE、PMFM算法的某路噪声功率估计归一化偏差不仅与该路输入信噪比有关,更取决于与其他路输入信噪比的差异。当非均匀组阵中各路信噪比相差较大时,由于未能充分利用多天线信号的相关信息,算法存在较大的合成损失。因此需要估计噪声协方差矩阵并加权至权值向量中,以降低噪声功率估计误差对合成性能的影响,减少合成损失。
3.2 本文合成算法原理
利用最优复权值向量得到的合成信号为

(9)
理论合成信噪比为[6]

(10)
信号功率归一化后,各路噪声功率有如下近似:

(11)
将合成信号的功率归一化后有

(12)
结合式(11)、(12)得到各路噪声功率估计

(13)
因此有噪声协方差矩阵的估计值

(14)
此时将上述噪声协方差矩阵估计值对角加载到现有算法中即可迭代求解非均匀组阵中的准最优复权值向量。同样,根据合成参考信号的不同,本文算法可分为DL-SUMPLE(Diagonal loading SUMPLE)与DL-PMFM(Diagonal loading Proposed Matrix-Free Method)两种算法。不同点就在于DL-PMFM算法中用于相关的参考信号是所有天线信号的加权和,故没有相位漂移现象,而且参考信号信噪比更高,算法合成性能更好。但由于去除了信号的自相关信息,DL-SUMPLE算法的收敛速度相对较快。
下面给出DL-PMFM迭代算法具体流程。
Step 2k-1次迭代后的合成信号并进行功率归一化:
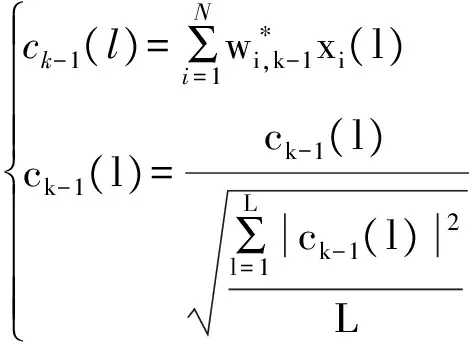
(15)

Step5 第k次迭代估计权值向量并归一化:
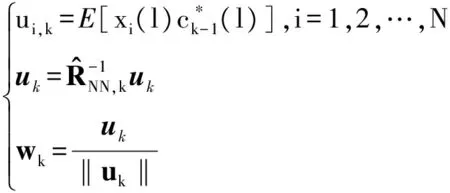
(16)
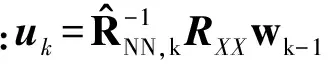
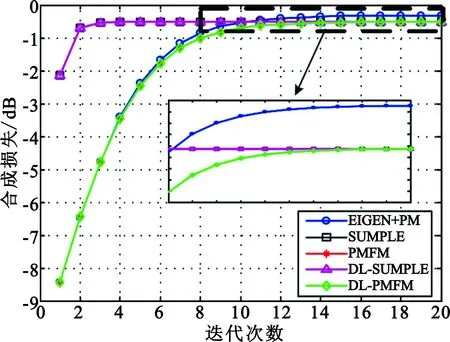
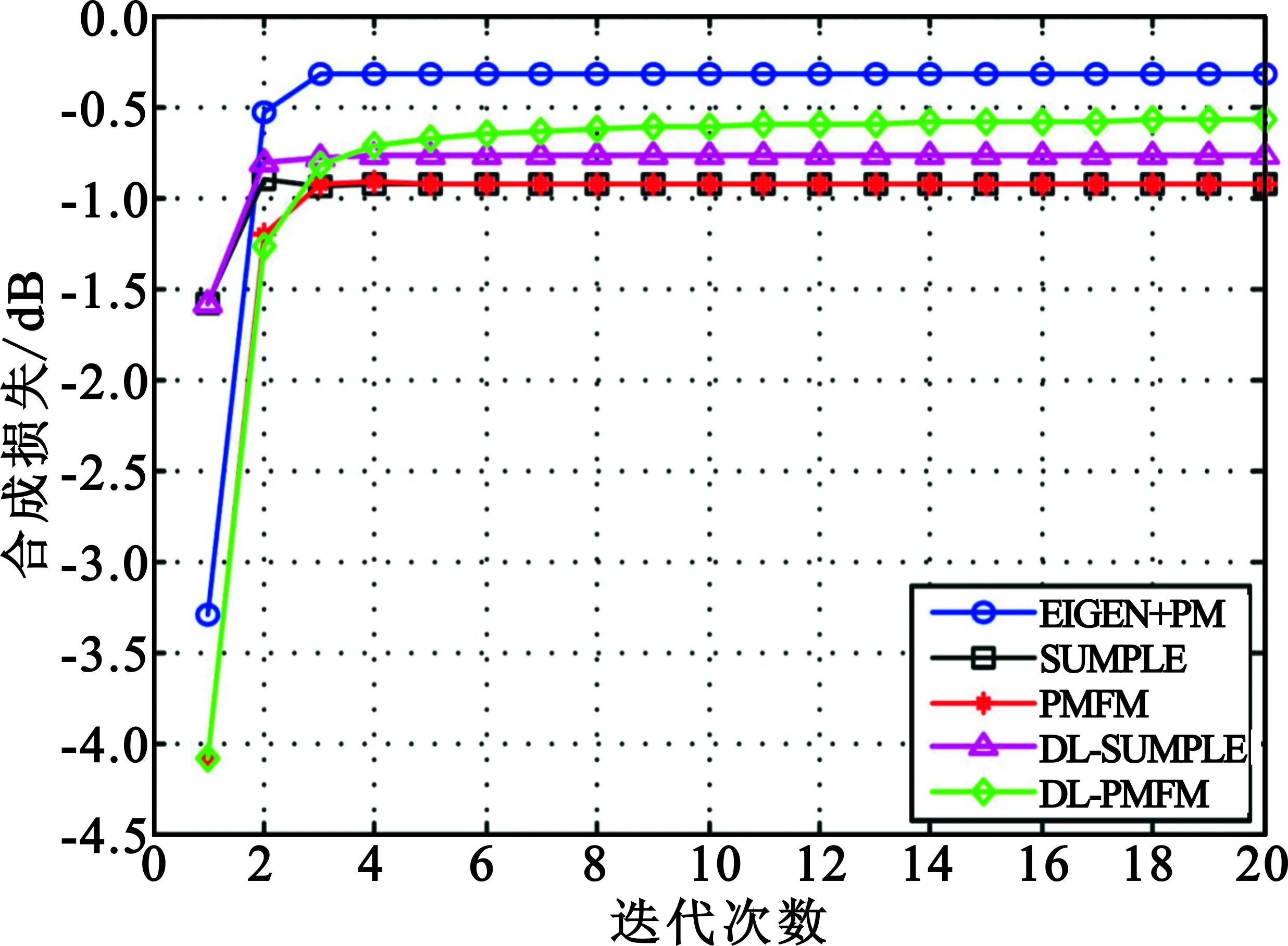
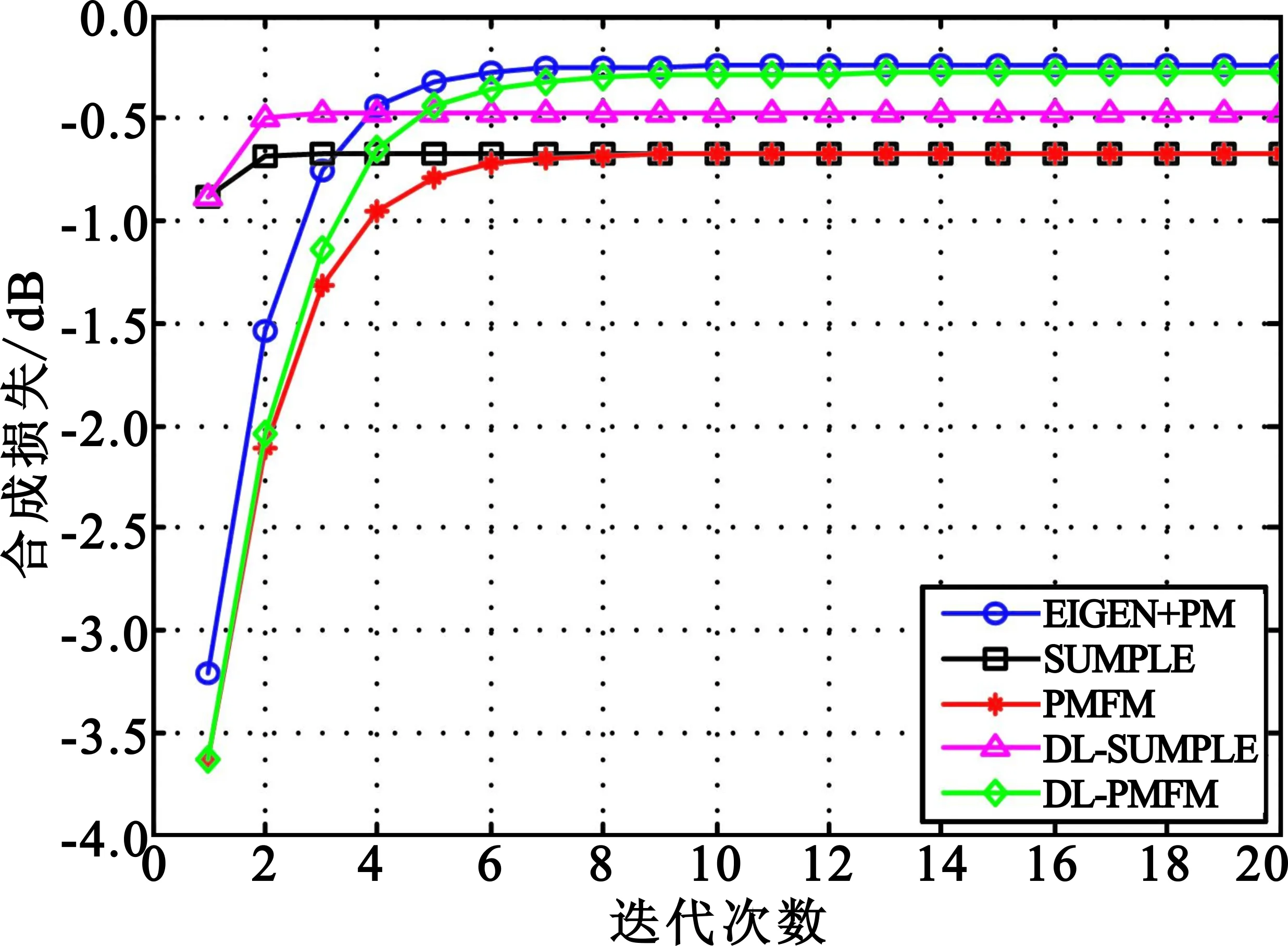
Step6 若k 在DL-PMFM算法迭代过程中加入Step4噪声方差收敛判断以避免算法发散,其中最小噪声方差可通过估计最大可能输入信噪比获得。相比于PMFM算法,DL-PMFM算法通过权值幅度快速估计各路噪声功率,并进行对角加载,因此在非均匀组阵中具有较小的合成损失,而收敛速度与PMFM算法相当。另外,DL-SUMPLE算法在Step5中参考合成信号需减去自身信号,其余与DL-PMFM算法相同,此处不再赘述。 3.3 本文算法性能分析 对式(11)求期望得 (17) 式(17)表明本文算法的噪声功率估计为有偏估计,其归一化偏差表示如下: (18) 与SUMPLE、PMFM算法不同,本文算法中各路噪声功率估计的归一化偏差只与该路输入信噪比和合成输出信噪比有关,并且输入信噪比越小,合成信噪比越大时,归一化偏差越小,此时估计越准确。总的归一化偏差为 (19) 对比式(8)和式(19)发现,非均匀组阵中各路噪声功率相差较大时,本文算法总的噪声功率估计的归一化偏差要小于现有算法,此时本文算法合成性能要优于现有算法,因此具有更小的合成损失。 表1对比分析了不同合成算法的计算复杂度。从表1可以看出,本文引入对角加载的合成算法相比SUMPLE、PMFM算法运算量略有增加,可认为4种算法复杂度相当。 表1 不同合成算法运算量对比Tab.1 Comparison of computation among different algorithms 在不同的组阵模式下,针对基于MSNR准则的Eigen[6]、SUMPLE[4]、PMFM[7]以及本文算法进行数值仿真。QPSK调制信号,根升余弦成型,滚降系数0.35,符号率64 ksymbol/s,中频频率100 kHz,采样率256 kHz,各路初始相差在0~2π之间随机分布,进行200次蒙特卡洛实验。 仿真实验1:首先对比分析功率归一化对信号合成算法的影响。其中各路信噪比在[-17.5,-12.5]dB间随机分布,信号幅度增益在[0.8,1.2]间随机分布,数据长度L=2 000,天线数N=10。假设Eigen算法的噪声协方差矩阵已知,求解过程采用PM算法。图1为功率归一化对合成性能的影响,此时SNRc=-4.55 dB。对比图1(a)、(b)可以发现,对接收信号进行功率归一化可以有效降低SUMPLE、PMFM算法的合成损失,尤其是在低信噪比情况下。原因在于输入信噪比较低时,经功率归一化后的噪声功率近似相等,此时上述算法都具有良好的合成性能。 (b)功率归一化后 仿真实验2:各路信号信噪比在[-10,0]dB之间随机分布,信号幅度增益在[0.8,1.2]之间随机分布,其余参数同仿真实验1,且合成前对各信号功率归一化。图2为各算法在迭代过程中合成损失对比,此时各路噪声功率均不相等,且相差较大,图中SUMPLE、PMFM算法合成损失较大达到0.93 dB,而本文的DL-SUMPLE算法迭代3次后即收敛,合成损失较小为0.77 dB,DL-PMFM算法损失更小仅0.57 dB,但收敛较慢,需迭代7次。原因在于DL-PMFM算法未去除自相关信息,参考信号信噪比更高,噪声功率估计更准确,合成性能更好,但收敛速度要稍慢。 图2 合成损失对比(SNRi∈[-10,0] dB) 仿真实验3:模拟大天线周围布设多个小口径天线场景。第一路信噪比为-5 dB,幅度增益为2,其余路信噪比在[-15,-10]dB之间随机分布,信号幅度增益在[0.8,1.2]之间随机分布,其余参数同仿真实验1。图3为各算法在迭代过程中合成损失对比。当大天线与多个小天线联合组阵时,该路噪声功率要远小于其余路。图3中SUMPLE、PMFM算法合成损失为0.67 dB,DL-SUMPLE算法合成损失较小为0.48 dB,而此时DL-PMFM算法合成性能趋近于基于MSNR的Eigen算法,合成损失仅0.28 dB。因为DL-SUMPLE算法去除了自身信号使得第一路信号的参考信号信噪比较低,噪声功率估计误差较大,最终合成损失明显大于DL-PMFM算法。 图3 合成损失对比(-5 dB+SNRi∈[-15 -10] dB) 图4给出了最好与最差两路信号合成权值的幅度对比。图中无论是DL-SUMPLE还是DL-PMFM算法的合成权值幅度都更接近于理论值,实现对信噪比高的信号加大权,提高信号的作用;信噪比低的信号加小权,抑制噪声影响,最终达到提高合成增益的目的。而且DL-PMFM算法中大天线的权值幅度估计非常准确,表明DL-PMFM算法在非均匀组阵中能够更加有效地利用强信号,使得合成性能明显优于DL-SUMPLE算法,能够趋近于理论值。 (a)SNR1=-5 dB (b)SNR10=-14.9 dB 本文在传统SUMPLE、PMFM算法模型基础上引入噪声功率盲估计与对角加载技术,提出了一种非均匀组阵中的合成算法。本文算法在非均匀组阵中的合成性能明显优于SUMPLE、PMFM算法,尤其在大天线与多个小天线组阵模式下,DL-PMFM算法合成性能能够趋于理论,而且本文算法的收敛速度、运算量与各模型算法相当。同时,算法收敛后能够得到噪声协方差矩阵的估计值,所以本文算法也可用于单输入多输出(Single Input Multiple Output,SIMO)系统的信噪比盲估计。但需要指出的是,本文的噪声功率估计算法为有偏估计,因此如何减小算法估计偏差,进一步提高合成性能可作为下一步工作重点展开。另外,如何将DL-PMFM算法高合成性能与DL-SUMPLE算法快收敛速度有机结合也是值得研究的重点和难点。 [1] 姚飞,匡麟玲,詹亚峰,等.深空通信天线组阵关键技术及其发展趋势[J].宇航学报,2010,31(10):2231-2238. YAO Fei,KUANG Linling,ZHAN Yafeng,et al.Key techniques and development trend of antenna arraying for deep space communication[J].Journal of Astronautics,2010,31(10):2231-2238.(in Chinese) [2] 舒逢春,江悟,张秀忠. 长基线天线组阵及其在深空探测中的应用[J].电波科学学报,2012,27(5):985-990. SHU Fengchun,JIANG Wu,ZHANG Xiuzhong. Long baseline antenna arraying and its applications to telemetry in deep space explorations[J].Chinese Journal of Radio Science,2012,27(5):985-990.(in Chinese) [3] 于志坚,李海涛,李小梅. 可扩充深空天线组阵技术研究与试验验证[J].遥测遥控,2015,36(6):1-8. YU Zhijian,LI Haitao,LI Xiaomei. Research and experiment verification on extendable deep space antenna arraying techniques[J].Journal of Telemetry,Tracking and Command,2015,36(6):1-8.(in Chinese) [4] ROGSTADD H. The SUMPLE algorithm for aligning arrays of receiving radio antennas:coherence achieved with less hardware and lower combing loss[R]. Pasadena,California:Jet Propulsion Laboratory,2005. [5] BAI Y F,WANG X H,GAO C J,et al.Adaptive correlation algorithm for aligning antenna arrays in deep space communication[J].Electronics Letters,2013,49(12):733-734. [6] CHEUNG K M. Eigen theory for optimal signal combining:a unified approach[R]. Pasadena,California:Jet Propulsion Laboratory,1996:1-9. [7] 史学书,王元钦. 深空组阵Eigen算法及其低信噪比合成性能分析[J].宇航学报,2009,11(6):2347-2353. SHI Xueshu,WANG Yuanqin. Performance of deep space seetion front eigen combining algorithm in low SNR condition[J].Journal of Astronautics,2009,11(6):2347-2353.(in Chinese) [8] 徐茂格,柴霖. 我国深空天线组阵技术现状与发展思考[J].电讯技术,2014,54(1):109-114. XU Maoge,CHAI Lin. Technical status and development suggestion of China′s deep space antenna arraying[J].Telecommunication Engineering,2014,54(1):109-114.(in Chinese) [9] 于晓黎,孙甲琦. 深空网异地多天线组阵及其发展[J].遥测遥控,2012,33(4):64-67. YU Xiaoli,SUN Jiaqi.Very long baseline multi-antenna arraying and the development in deep space network[J].Journal of Telemetry,Tracking and Command,2012,33(4):64-67.(in Chinese) [10] 孔德庆,施浒立. 非均匀天线组阵SUMPLE权值信噪比及信号合成性能分析[J].宇航学报,2009,30(5):1941-1946. KONG Deqing,SHI Huli. Study of weights performance and combining loss of SUMPLE algorithm for non-uniform antenna arraying[J].Journal of Astronautics,2009,30(5):1941-1946.(in Chinese) [11] 孔德庆,施浒立.非均匀天线组阵 SUMPLE 合成相位补偿及信号强度估计[J].电波科学学报,2009,24(4):632-636. KONG Deqing,SHI Huli. Phase wandering correction and signal intensity estimation of SUMPLE algorithm for non-uniform antenna arraying[J].Chinese Journal of Radio Science,2009,24(4):632-636.(in Chinese) [12] ZHANG J Y,ZHANG X Y,LUO B W. A novel combining weights estimate algorithm for short burst signals based on antenna array[C]//Proceedings of 12th IEEE International Conference on Communication Technology.Nanjing:IEEE,2010:247-250. [13] 赵晓明,偶晓娟,陈学军,等.深空天线组阵相关合成算法的Simulink仿真与分析[J].电讯技术,2015,55(5):509-515. ZHAO Xiaoming,OU Xiaojuan,CHEN Xuejun,et al.Simulink simulation and analysis of correlating and combining algorithms for antenna arraying in deep space network[J].Telecommunication Engineering,2015,55(5):509-515.(in Chinese) A Combining Algorithm Using Diagonal Loading forNon-uniform Antenna Arraying WU Jinga,b,JIANG Hongyua,LI Binga,QI Ganga (a.Institute of Electronic Engineering;b.Graduate School,China Academy of Engineering Physics,Mianyang 621999,China) A new combining algorithm for non-uniform arraying is proposed to improve the poor performance of the SUMPLE and PMFM(Proposed Matrix-Free Method)algorithm,by applying diagonal loading technique to the SUMPLE and PMFM algorithm model separately. The proposed algorithm,which is diagonal loaded by the estimated noise power based on the weight amplitude,can solve the quasi-optimal weight vector iteratively. Theoretical analysis and numerical simulations show that the novel algorithm can achieve obviously lower combining loss for non-uniform antenna arraying,with similar computation complexity and convergence rate to the SUMPLE and PMFM model algorithm. Therefore,it is a strong candidate for engineering application in the actual antenna arraying system. antenna arraying;non-uniform antenna arraying;combining algorithm;diagonal loading 10.3969/j.issn.1001-893x.2017.06.016 伍警,蒋鸿宇,李兵,等.非均匀天线组阵中引入对角加载的合成算法[J].电讯技术,2017,57(6):710-715.[WU Jing,JIANG Hongyu,LI Bing,et al.A combining algorithm using diagonal loading for non-uniform antenna arraying[J].Telecommunication Engineering,2017,57(6):710-715.] 2016-10-10; 2017-03-02 Received date:2016-10-10;Revised date:2017-03-02 中国工程物理研究院科学技术发展基金项目(2015A0403001) TN820.1 A 1001-893X(2017)06-0710-06 伍 警(1992—),男,湖南常德人,2014年于中国科学技术大学获电子工程与信息科学专业学士学位,现为硕士研究生,主要研究方向为多天线信号合成技术; Email:15656569752@163.com 蒋鸿宇(1982—),男,四川绵阳人,2012年于中国工程物理研究院研究生院获博士学位,现为副研究员,主要研究方向为软件无线电与宽带数字接收机; Email:doherty2004@163.com 李 兵(1984—),男,陕西宝鸡人,2010年于西安交通大学获硕士学位,现为助理研究员,主要研究方向为高速数字信号处理、数字接收机; Email:lechateler@163.com 漆 钢(1988—),男,湖南湘潭人,2013年于中国工程物理研究院研究生院获硕士学位,现为助理研究员,主要研究方向为通信与信息系统、数字信号处理。 Email:gqi228cq@yahoo.com.cn **通信作者:15656569752@163.com Corresponding author:15656569752@163.coma,b,蒋鸿宇a,李 兵a,漆 钢a

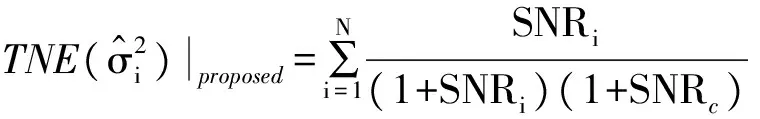

4 数值仿真


5 结束语

