复杂通信网络的地理位置聚集性社团发现和可视化*

2017-06-23代翔

电讯技术 2017年6期

关键词：标号社团可视化

代翔

(中国西南电子技术研究所，成都610036)

复杂通信网络的地理位置聚集性社团发现和可视化*

代翔**

(中国西南电子技术研究所，成都610036)

针对以通信网络为代表的一类复杂网络地理位置信息的聚集性与网络结构一定程度上的正相关性，探讨了将地理位置信息带入特定的复杂网络的社团发现和可视化任务中，改进传统的标号传播和力导引算法，提前进行网络的地理位置聚类分析，并对标号传播的和力导引的迭代过程引入基于地理位置的限制性条件，避免无意义的振荡。实验证明，提出的方法既可以加快社团发现和可视化算法的收敛速度，也可以通过地理位置对社团分布的影响提高快速社团发现算法的性能。针对存在地理位置聚集性的复杂网络数据，该方法无论在收敛时间还是社团发现结果(Q值)上都有较大提升。

复杂通信网络；社团发现；地理位置；标号传播；力导引

1 引言

现实世界中存在着大量的网络结构，例如人际关系网络、工作协作网络、传染病传播网络以及新近产生的通信网络和社交网络等。由于这些结构有着共同的“自组织、自相似、吸引子、小世界、无标度”等复杂特性，所以被统称为复杂网络[1]。社团发现是研究复杂网络结构以及可视化的重要基础性工作[2]。对于大规模复杂网络，通过社团发现，以及可视化标记，能够较好地帮助使用者了解复杂关系网络的社团分布情况，对分析复杂网络的拓扑结构、理解复杂网络的功能、发现复杂网络中的隐藏规律以及预测复杂网络的行为都有十分重要的意义[3]。

传统的社团发现算法大多着眼于网络的拓扑结构本身，仅仅拓扑关系，而忽略了节点的特征，如地理位置信息，使得传统算法在不够高效的同时，不能有效地反映节点的用户群的地理聚集性。而在以通信网络为代表的复杂网络中，社团的地理聚集性显而易见。针对这一问题，本文提出一种基于地理位置信息的可视化复杂网络快速社团发现算法，将用户的地理位置等用户群信息加入社团发现的过程，并在可视化的网络展示中进行标记，给使用者提供一种基于关系社团以及用户群的社团分布展示。这种社团分布更能利用节点在地理位置和关系上的地位，辅助节点影响力分析。

2 复杂网络的社团发现

2.1 复杂网络中的社团

网络是由节点(node)和边(edge)组成的拓扑结构，被广泛用于表示各种现实世界中的交互系统，例如食物链、人际关系等。当所表示的系统节点数据巨大，节点间关系错综复杂时，这样的网络被称为复杂网络。尽管节点间关系复杂，但是大多数情况下却并不完全随机，而是满足某些特定的规律，如无尺度、小世界等。

社团是指一组相互之间关系紧密，而与外界关系疏远的节点的集合。在复杂网络中社团的发现有着十分重要的意义，例如：能够找到一群爱好相似的用户，或者是联系紧密的犯罪团体。

模块度函数是一个定量描述网络中社团的数学工具。如果网络的一组社团划分中所有内部的连线所占的比例越大，则该社团划分越好。但是，为了惩罚大社团的优势，所以需要与一个随机网络中所有社团内部节点的连线数所占比例期望值相减，而得到的这个差值就是网络社团划分的模块度，计算这一数值的函数称为模块度函数。令ci为节点i分配的社团，社团内部节点的连线所占的比例可以表示为

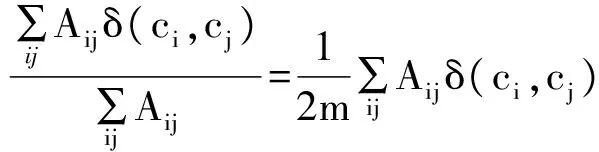
(1)

式中：Aij表示i、j两点间的连线数，有连线则为1，否则为0；δ(ci,cj)为δ函数，即ci=cj时值为1，反之为0；m表示网络中连线的数量。在随机网络中，i、j两节点相连的概率为(kikj)/2m，ki为节点i的度(degree)。所以，描述社团划分模块化水平的Q函数为

(2)

如果对一个复杂网络进行随机划分，则模块度Q取值应接近于0。当社团划分越好时，Q的取值越大，但是通常不可能达到理论上的最大值1,一般认为现实世界中的社团模块度Q值在0.3～0.7之间。

2.2 传统的社团发现算法

由于社团的判定依赖于模块度的计算，所以通过计算模块度来进行社团发现便成为了最显而易见的方法。基本思路是穷举所有的可能子社团组合的方式，选择其中模块度最大的那一种作为下一步迭代的社团组合，反复迭代直到模块度不再增加为止。这种方法理论上并不能得到最佳的社团划分，而是会陷入局部最优解。更大的问题是这一计算求解的过程是一个非决定性多项式时间完全问题，不能应用于规模较大的网络。近年来研究人员对模块度优化算法进行了一系列的改进，引入社团对层次性和重叠性的考量以及各种启发性的近似算法，使其在计算复杂度问题上都有不小的改进[2]。

研究人员发现网络社团总是存在着某种层次结构，例如一个大社团包含一系列的小社团，这种特性称为社团的层次性，从而设计了一系列的层次性社团发现算法[4]。具体地，层次化的算法又分为自上而下的分裂算法和自下而上的凝聚算法两种。较早出现的文献中大多采用的是分裂算法，但是其并没有根本上的解决计算复杂度，以及无法识别小社团的分辨率问题。凝聚算法由于是自下而上的，天然的能够应对分辨率问题。本文所改进的标号传播算法[5]就是一类凝聚算法。但是真实的社团并不一定存在层次结构，在这种情况下层次方法所产的伪层次反而会带来各种问题。

传统的社团发现算法仅仅考虑复杂网络本身的结构，在解决实际问题时，总是试图将节点、边的各种属性先抽取并建模到复杂网络中，再进行结构的分析和社团的发现，这种思路虽然有较好的普适性，但是无形中极大浪费了实际系统中已有的知识，甚至可能造成已知社团结构的丢失等问题。

2.3 通信网络中的社团与地理位置聚集性

通信网络中的地理位置聚集性和社团的关系是显而易见，无论是从实际经验出发(与本地亲友交往的频次远高于外地亲友)，还是研究人员的定量研究成果[6-8]，都肯定了这一点。文献[6]从推荐系统的角度出发，指出历史行为轨迹越相近的人，其在兴趣方面的相似度越高，从而越有可能建立起某种关联关系。基于这一点，文献[7]通过地理位置的相似性，帮助用户建立交互关系，即社群关系。其背后的逻辑与本文非常类似：都是通过地理位置信息来辅助建立线上-线下社群的映射关系。文献[8]系统性地讲述了通信网络中的地理位置聚集性问题，不过是以环保节能作为出发点进行研究。

简单地将线下的地理位置聚团信息映射为社团关系显然也是不合理的。现代人的生活经验是，虽然我有大量的距离较近的亲密好友，但是住在隔壁的邻居却大多并不认识。即便是在社区文化更加发达的美国，与邻居间的通信行为占比也不到5%[9]。从复杂网络的层次性特性来说，地理位置聚团信息可以在某种程度上看成是社团关系的上层关系。

3 基于地理位置的社团发现和可视化

基于上述认识，在对通信网络这一特殊的包含有显著地理信息聚集性的复杂网络进行分析时，可以利用其地理信息聚集性设计一个更加快速和高效的社团发现算法，基本思路是：先对通信网络进行地理位置聚团分析，形成群组划分的初始信息，再通过一个带一定限制性的算法来进行社团发现，从而达到利用地理位置信息进行快速启动和避免算法反复迭代的目的。具体地，我们可以通过改造标号传播算法来实现这一思想。

3.1 基于地理位置聚类的快速社团发现

地理位置信息作为一个二维平面信息，几乎所有的聚类算法都可以用来对其进行聚团分析，常见的算法有K均值聚类(K-means)、凝聚型的层次聚类、模糊聚类的模糊C均值聚类(Fuzzy C-means,FCM)以及基于神经网络的聚类等。由于这部分内容并非本文重点，我们不对上述算法进行过多的分析和比较，只是通过经验以及一系列的对比实验，选定了吸引子传播(Affinity Propagation,AP)聚类算法作为地理位置聚团分析的聚类算法[10]。与K-means等最常见的聚类算法相比，AP算法最大的好处是不需要指定聚类的个数，而是通过优先权(Preference)和阻尼因子(Damping factor)来控制最终聚类的大小，从而能够很容易地对地理位置聚团的大小进行调节。另一方面，AP算法对初始值不敏感，即使多次执行AP聚类算法得到的结果完全一样，这样的好处是算法的可重复性较高。由于地理位置聚团只是本文工作的第一个步骤，所以可重复性显得尤为重要。

接下来的社团发现过程，我们采用一个改进的标号传播算法来进行。标号传播算法时间复杂度仅为O(n)，十分适合用于大型网络的社团发现。另一方面，标号传播算法的执行过程伴随着节点颜色的连续变化，十分适用于可视化的系统。但是，标号传播算法是一个自下而上的凝聚算法。为了利用地理位置聚团分析的结果，我们引入了色谱的概念，重新定义了标号传播的过程。

具体地，从一个通信网络的数据集出发，进行地理位置聚类和社团发现的算法流程如下：

Step 1 建立通信关系网络。网络中节点为每个通信活动的参与者(手机用户)，如果节点间有通信行为，则存在一条边，边的权重为通信行为的次数。

Step 2 提取通信网络中的位置信息。本文所针对的是移动通信网络数据，所以可以根据每次呼叫的基站编号数据来判断节点的大致位置。提取之后，对每次呼叫行为记录节点之间的距离，如下：

distance(i,j)=mincall_distance(i,j)，

(3)

即节点间的距离定义为用户间呼叫的最小距离。

Step 3 将上述定义的节点间距离distance(i,j)代入到AP聚类算法中，进行地理位置聚团分析。过程中需要通过调整优先权和阻尼因子的取值来控制最终聚类的大小，实际的应用场景对应的取值我们会在实验中具体给出。完成地理位置聚团分析后，每个节点根据结果标记其所属聚团号码。

至此，完成节点的地理位置聚类，根据地理位置聚类的结果分配节点的初始着色，进行受限制的标号传播。

Step 4 采用HSB(Hue,Saturation,Brightness)模型对每个节点进行着色。

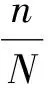
Step4-2 对聚团中的每个节点，通过一个取值在[s,100%]的随机数作为它的S值。其中s为算法的逃逸系数，如果s取值越大，则最终的社团发现结果越依赖于前期的聚团结果了；如果s取值越小，则前期的聚团结果对最终结果的影响越不明显。

Step4-3 节点初始着色的H值即为其所属聚团的H值，节点的V值简单设定为100%。至此完成节点初始着色。

Step5 颜色相同的节点分配一个社团号。

Step6 遍历每个节点i，计算每个节点vi与所有相邻社群gk之间的颜色契合度，节点和社群的颜色契合度定义如下：

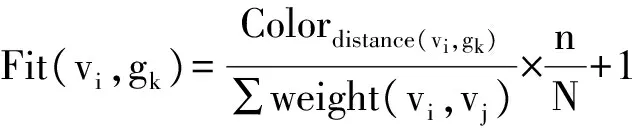
(4)

式中：vj为社群gk中的节点，n为上一次迭代过程中改变了节点的社群的个数，N为复杂网络中社群的总个数，n初始值设为N。

Step 7 将节点i的社团号更改为最相关社团的社团号，如果相关性最高的有多个，则保持当前的社团号不变。

Step 8 遍历一遍后，若此时网络没有达到稳定(本次遍历有足够少的节点改变了社团号)，则重新进行Step 5～7;否则，社团发现完成。

算法的总体流程非常简单，如图1所示，分为地理信息聚类、初始着色、标号传播3个步骤。其中依赖于地理信息聚类结果的初始着色是本算法的核心，通过这个在HSB空间上的初始着色算法的设计，将地理聚类的信息传递到了标号传播中。加入的逃逸系数s是控制最终算法执行结果的一个重要手段，在具体的执行过程中根据网络的地理聚集性的强弱来对s的取值进行设定。之所以采用HSB空间是考虑到接下来的可视化效果，色相的相似性更容易被人眼接收和感知，从而更好地理解标号传播的迭代过程；而明度的统一使得每个节点的重要性都能够相同被可视化表示。

图1 社团发现算法总体流程

Fig.1 Flow chart of group detecting algorithm

颜色契合度的加入是避免振荡的一个重要手段，而容易陷入反复无意义的振荡是标号传播算法最大的缺陷之一。标号传播算法虽然时间复杂度为O(n)，但是随着网络的复杂性增加，标号传播的振荡次数会显著增长，反映出来在实际应用中的性能下降。本算法基于标号传播算法，时间复杂度与传统的标号传播算法相同，都是O(n)。但是，由于通过前期的地理位置聚类以及色谱的标注，再加上修改了标号传播的迭代方法，节点只会加入最“契合”的群组，而不是随意振荡，从而使得迭代次数相对于传统的标号传播算法有很大的下降，很大程度上避免了标号传播算法中的节点振荡问题。而与传统的对标号传播算法的改进不同的是，本算法不是通过限定节点的活跃度来避免振荡，所以最终的社团发现结果更有说服力。

在社团发现的效果方面，本算法加入了地理位置的影响因素，因而能够很好地发现在地理位置上存在较好聚集性的社团，同时使得完全与地理位置无关的社团的划分效果不可避免地有一定程度的降低。对特定的应用而言(例如避免群体事件的发生，在地理位置上不具备聚集性的社团不会成为最终感兴趣的结果)，这一结果不但完全可以接受，而且过滤了大量的无效社团，比一般性的社团发现算法更有实际应用价值。另一方面，本算法将节点的线下关系映射到关系网络中，有利于对网络结构的观察，为下一步的可视化提供了坚实的基础。

3.2 基于地理位置的社团发现可视化迭代

复杂网络分析只是人们从大数据中获取知识的一个步骤。由于计算机自动分析技术的不完善，人工参与不可避免，于是可视化成为了数据分析的一个重要组成部分。通过可视化能够让人参与到大数据分析的过程中，从而更好地结合人类和机器的分析能力[11]。社团发现的一个重要目的是进行可视化展示，而标记传播算法由于有标记的存在，也是最天然的适用于可视化迭代的社团发现算法。通过算法迭代的过程，颜色和距离上的逐渐聚集让人更好地理解复杂网络中的社团，从而进一步学习和发现复杂网络中的各种知识。

为了保证复杂网络中的社团可视化便于理解，一般来说会采用着色和节点聚集两种方法进行展示。着色方法前文已说明，此处不再赘述。节点聚集的方法是复杂网络可视化的另一个比较大的基础性问题，其目标是让同属于一个社团的节点在空间(或者平面)位置上接近，不属于同一个社团的节点在空间(或者平面)位置上较远。但是，由于需要计算任意两个节点之间的关系，所以时间复杂度是O(n2)，这在一个大规模的复杂网络中是一个极大的计算开销。如果我们进一步考虑将社团发现的可视化过程迭代显示出来，则需要乘以迭代次数，时间复杂度进一步提升。

我们提出了基于地理位置的改进力导引布局算法来解决这一问题。力导引算法是一个经典的复杂网络布局算法，通过计算节点之间的斥力和边上的引力来进行复杂网络的布局。其缺点在于力导引布局的计算本身也是一个迭代的过程，再加上一个迭代的社团发现过程，将会使迭代次数爆炸性增长。我们把力导引的迭代和标号发现的迭代融合到一起，再加入地理位置的辅助信息，能够极大地加快这一可视化的过程，降低计算复杂度。

首先定义引力和斥力。与经典力导引不同，我们定义节点还会受到自身社团的引力和其他社团的斥力，具体如下：

s1(ek=(vi,vj))=-K(r-L)，

(5)

(6)

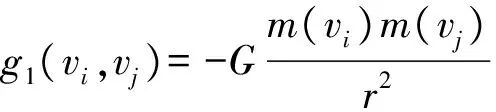
(7)

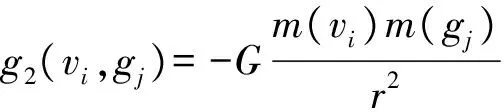
(8)

式中：s1和s2、g1和g2表示节点受到的引力和斥力，分别来自于边、本社团质心、其他节点和其他社团质心；K为弹性边的弹性系数；L表示默认弹性边的原长；G表示引力常量，在这里并不等同于万有引力常量。通过调整K、L、G的值可以使布局变得更加紧凑或者松散。

在重新定义了引力和斥力后，下面给出具体的基于地理位置的改进力导引布局算法步骤：

Step 1 在平面上按照地理位置放置网络节点的初始位置。

Step 2 按照3.1节中基于地理位置聚类的快速社团发现算法Step 1～3计算节点的初始社团，并对其进行着色标记。

Step 3 计算每个社团的质心位置以及重量。

Step 4 根据上文所定义的引力和斥力公式，对每个节点计算受力大小和方向，并根据受力计算节点位移δ=f·d，其中f为总的受力大小，d为位移常量。

Step 5 按照3.1节中基于地理位置聚类的快速社团发现算法Step 5～8进行一次受限制的标号传播过程。

Step 6 重复Step 3～5，直到社团稳定不发生变化，则算法终止。

本算法将力导引的迭代过程和标号传播的迭代过程整合到一起，引入了社团对节点的作用力，一方面加强社团的可视化效果，另一方面帮助节点快速进行定位。本算法的核心在于这一全新的引力和斥力的定义和计算的方式。传统的力导引算法只是对自然界中的引力和斥力进行机械地模仿，缺乏合理的物理学基础理论的支撑，实际表现上也有相当多的缺陷。我们跳出其简陋的物理模型，从实际效果出发来进行力的设计，使得社团结构能够快速地被显现，社团越早被发现，则社团的结构越容易被可视化表示；并且使用节点的地理位置进行辅助，一方面降低了迭代过程的计算复杂性，另一方面减少了节点的无谓振荡，无论迭代性能还是可视化效果都有较大的提升。

4 算法测试

4.1 实验环境及算法测试数据

实际的测试采用某地的真实通信网络数据集，该数据集包含了251 231个节点以及1 031 449条连线(仅考虑数据集节点间的通信行为)，每次通信行为都包含了通信参与者双方的地理位置信息(基站信息)。

表1代表了用户之间的消息记录，每条记录代表两个数字节点具有关系。同时，表中标记了每次通信的LAC和CELLID信息，通过这些信息很容易查询到具体的位置信息,因数据敏感，表中用“*”代替。由于节点不可避免地处于运动中，我们把节点最后一次通信行为的位置作为节点的位置。

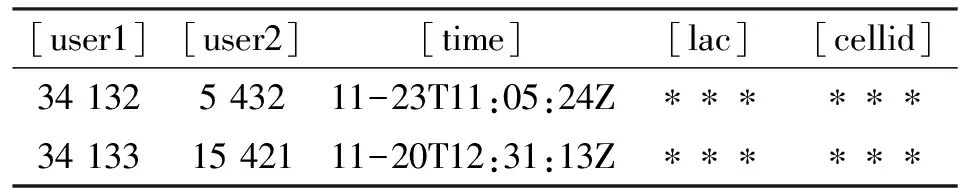
表1 消息记录示例Tab.1 Example of message record

4.2 测试步骤

本文的测试分两个步骤进行，分别是针对算法的收敛时间和算法的最终结果的测试。我们选用经典的标号传播算法进行对比测试，以验证本文算法改进的有效性。

分析算法的执行步骤可以很容易理解，标号传播类算法都是通过多次遍历网络的边集以进行社团发现，因此，随着数据量的增加，算法从达到收敛状态的时间是等比增加的，也就是说，算法都具备线性的时间复杂度。我们通过删除数据集中的部分节点来修改数据集节点数的大小，对比测试两个算法计算时间的同时，验证其算法的时间是否随着节点个数的变化呈现线性关系。所有测试结果均重复10次取平均值。

我们在测试中使用模块化函数定量分析社团划分结果的模块化水平，从而对算法的执行结果进行定量分析。模块度Q值取值在0～1之间，社团划分效果越好Q值越大，但是会受到实际社团的影响，很难对其进行评价，例如：网络中如果不存在明显社团，则无论算法如何优秀，都不可能得到较好的Q值。所以，只能过通过对比试验来判断算法的有效性。与算法收敛时间测试相同，社团划分效果测试同样采用相同的多组数据集，比较在不同数据规模下两个算法的执行效果。

4.3 测试结果与分析

使用带有地理位置的通信网络真实数据集，进行社团发现算法度对比分析测试。首先测试算法的执行速度，使用传统的标号传播社团发现算法和基于地理位置聚类的快速社团发现算法，分别对大小不相同的几个数据集进行社团发现测试后，其执行时间对比如表2所示。

表2 算法时间对比Tab.2 Time consumption vs. network scale

为了有一个更直观的认识，将表中各种数据绘制为折线图，以对比两种算法执行社团发现的收敛时间随节点规模的变化关系，如图2所示。

特别需要说明的是，由于基于地理位置聚类的快速社团发现算法包含了两步走的处理过程，所以在社团较小的极端情况下耗时稍高。

从图2中可以看出，两种算法在时间消耗上基本符合线性增长的特征，这与前文对其时间复杂度的分析对应。在进行大规模网络社团发现时，传统的标号传播算法由于存在节点的振荡，算法时间与线性拟合的曲线有较大的偏离，表现为网络越大，振荡越严重，同时节点振荡的程度也与网络的模块度有一定关系。本文中的限制性标号传播算法由于采用两步走的策略，通过一个快速的地理位置聚类度步骤减少了标号传播度迭代次数，避免了节点振荡，从而可以消耗更少的时间达到收敛。

两个算法的社团发现效果测试结果如表3所示。

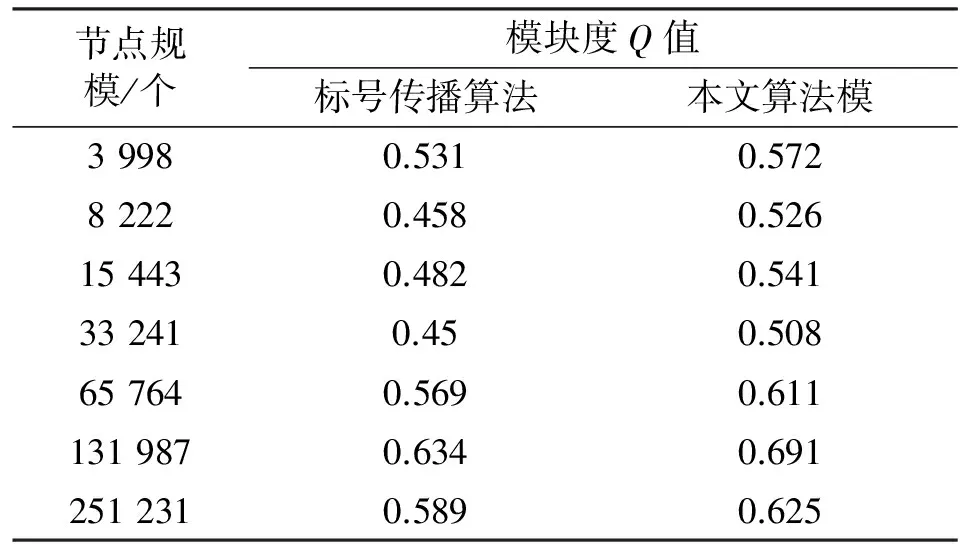
表3 算法Q值比较Tab.3 Q value vs. network scale

将测试数据绘制为折线图，对比两种社团发现算法的模块度，如图3所示。

基于地理位置聚类的限制性标号传播算法较标号传播社团发现的模块度值明显有所提升，可以得出结论：算法的其社团发现效果要好于传统的标号传播社团发现。

可视化是本文算法的另一个组成部分，但是，对可视化复杂网络缺乏客观的评价标准，使得较难以用过数值对其进行可视化的评价。这里还是给出一个直观的例子，试图通过这个示例来解释本文中所述的方法和传统方法的区别。

我们抽取除了一个包含76个节点的图进行了可视化对比展示(见图4)，并以颜色区分不同的社团。在图4(a)中用普通的力导引算法将网络中的节点在平面上进行了可视化布局展示，图4(b)中加入了地理位置的影响。表面上看，图4(a)的节点布局更合理，每个社团的可视化聚集性更好，更能反映网络中的社团结构。但是，由于图4(b)中考虑了节点的实际位置，使得图4(b)虽然看起来不漂亮，但是却包含了更多的可视化信息。从知识表达的角度来说，我们认为图4(b)的结果会更好一些。

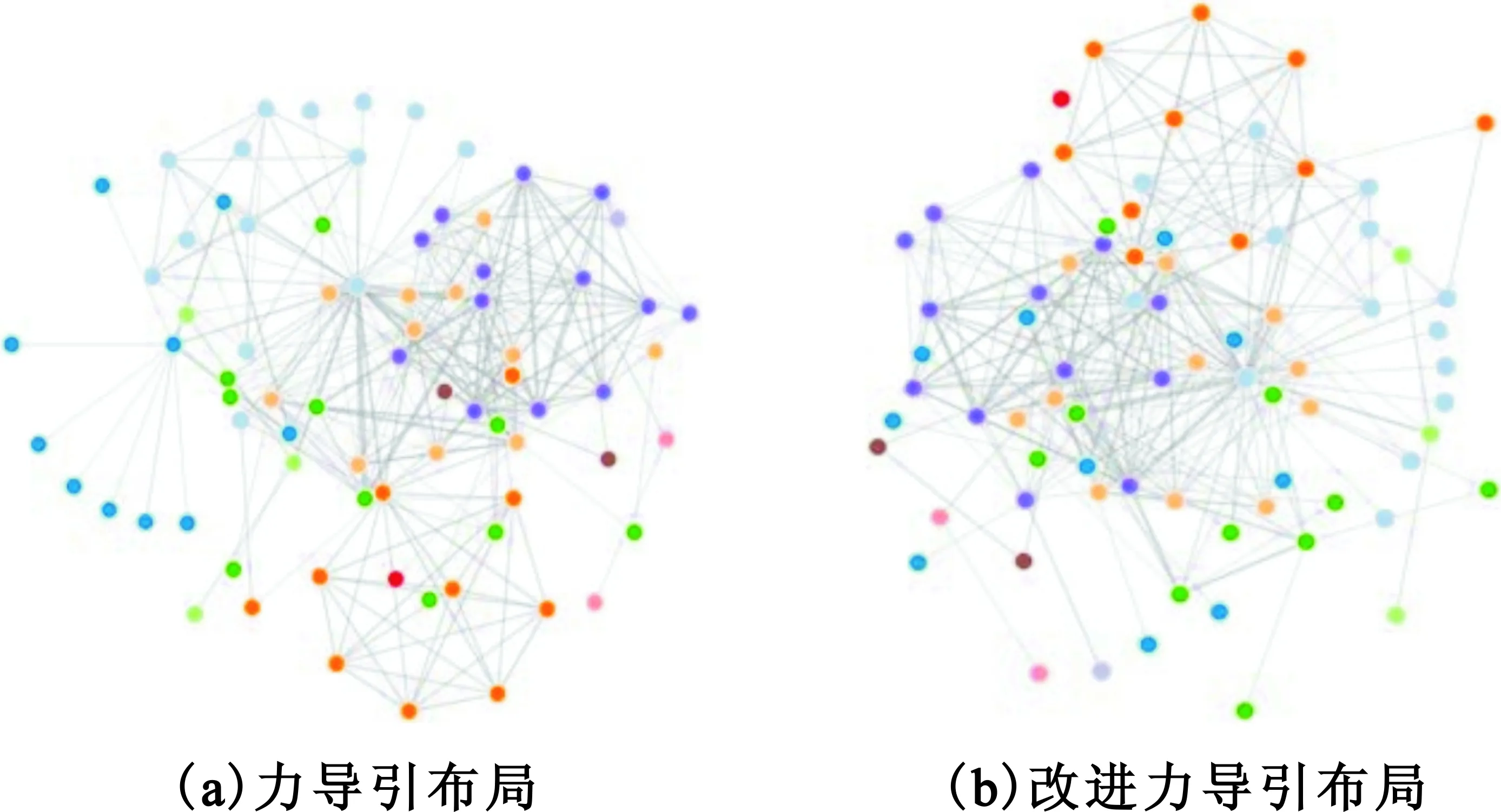
图4 社团发现可视化效果对比测试

从上述测试结果可以发现，加入地理位置信息之后的社团发现和可视化算法在收敛时间、Q值以及可视化效果方面均优于传统算法，并且在社团发现的结果中体现了地理位置的聚团性。因此，我们可以得出结论：该算法可以适用于实际通信数据的可视化分析。

5 结束语

本文讨论了参考节点地理位置信息的情况下对复杂通信网络的社群划分和可视化两个基本问题进行优化的方法，主要贡献在于：

(1)提出一种基于地理位置信息的限制性标号传播算法，通过地理位置信息帮助初始化编号传播网络，并且限制节点的无目的性振荡，提高了标号传播社群发现的性能;

(2)提出了一种基于地理位置信息的改进力导引布局算法，将力导引算法和标号传播社群发现在地理位置为基础的信息上进行融合迭代，使得一方面社群发现的过程可视化，另一方面可视化效果也得到了提升。

本文的直接结论只有益于通信网络，在其他结构特征下的复杂网络中也许并不适用，但是所提出的采用节点信息辅助社群划分和可视化的思路是普适的，可以作为复杂网络分析的一项基本手段。进一步的研究可着眼于不同业务网络的结构特征与节点属性的关联分析，以及深度融合节点特征的网络结构分析算法。

[1] 何大韧,刘宗华,汪秉宏. 复杂系统与复杂网络[M].北京：高等教育出版社,2009.

[2] HARENBERG S,BELLO,G,GJELTEMA L,et al.Community detection in large-scale networks: a survey and empirical evaluation[J].Wiley Interdisciplinary Reviews: Computational Statistics，2014(6): 426-439.

[3] CORREAC D. History and evolution of social network visualization[M].New York：Springer,2014: 677-695.

[4] TRUSINA A,MASLOV S,MINNHAGENP,et al.Hierarchy measures in complex networks[J].Physical Review Letters,2004,92(17): 178702-1-178702-4.

[5] 张俊丽,常艳丽,师文. 标签传播算法理论及其应用研究综述[J].计算机应用研究,2013,30(1): 21-25. ZHANG Junli,CHANG Yanli,SHI Wen. Overview on label propagation algorithm and applications[J].Application Research of Computers,2013,30(1): 21-25.(in Chinese)

[6] LI Q,ZHENG Y,XIE X,et al.Mining user similarity based on location history[C]//Proceedings of the 16th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems. Irvine,CA,USA:ACM,2008:1-10.

[7] ZHENG Y,XIE X,MA W Y. GeoLife: a collaborative social networking service among user,location and trajectory[J].IEEE Data Engineering Bulletin,2010,33(2):32-39.

[8] WANG X,VASILAKOSA V,CHEN M,et al.A survey of green mobile networks: opportunities and challenges[J].Mobile Networks and Applications,2012,17(1):4-20.

[9] KASSEN M. A promising phenomenon of open data: a case study of the Chicago open data project[J].Government Information Quarterly,2013,30(4): 508-513.

[10] PAVLOPOULOS G A,MOSCHOPOULOSC N,HOOPER S D,et al.Clust: a clustering and visualization toolbox[J].Bioinformatics,2009,25(15): 1994-1996.

[11] BECK F,BURCH M,DIEHLS,et al.A taxonomy and survey of dynamic graph visualization[J].Computer Graphics Forum,2016,36(1): 133-159.

Complex Communication Network Geolocation BasedCommunity Detection and Visualization

DAI Xiang

(Southwest China Institute of Electronic Technology,Chengdu 610036，China)

The geolocation is believed to have certain positive correlation with network structure in the communication networks,shopping network and other complex networks.The geolocation information is introduced into the task of complex network group detecting and visualization to improve the traditional label propagation algorithm and force-directed graph drawing algorithm. By performing the geolocation based clustering in advance,and then adding the geolocation based restriction in the iterative process,meaningless oscillations can be greatly minimized. The experiment proves that this scheme can speed up the discovery of community and the convergence speed of the algorithm can also be added to the influence of geographical location on the distribution of the community,and the performance of the fast community discovery algorithm can be improved both in convergence time and community discovery(Qvalue).

complex communication network;community detection;label propagation;force-directed graph

2017-03-09；

2017-05-03 Received date:2017-03-09；Revised date：2017-05-03

“十三五”国防预研基金

10.3969/j.issn.1001-893x.2017.06.001

代翔.复杂通信网络的地理位置聚集性社团发现和可视化[J].电讯技术，2017,57(6):615-621.[DAI Xiang.Complex communication network geolocation based community detection and visualization[J].Telecommunication Engineering,2017,57(6):615-621.]

TN921

1001-893X(2017)06-0615-07