新型弯剪型防屈曲软钢阻尼器的滞回性能研究

郑 宏, 全 凯, 丁双杰

(长安大学 建筑工程学院,陕西 西安 710061)

新型弯剪型防屈曲软钢阻尼器的滞回性能研究

郑 宏, 全 凯, 丁双杰

(长安大学 建筑工程学院,陕西 西安 710061)

金属阻尼器的耗能能力极大地依赖于耗能构件在轴向、弯曲或剪切荷载下的塑性变形及滞回响应。本文提出一种新型弯剪型防屈曲软钢阻尼器，该阻尼器主要由3个部分组成，两个承受弯曲荷载的X形端板，一块主要承受剪切荷载的软钢腹板，以及两块限制腹板面外变形的外约束加劲钢板。利用ABAQUS有限元软件对比分析了不同形式阻尼器的3个试件，试件区别在于是否存在X形端板和外约束加劲钢板。为了对该新型阻尼器进一步优化，对剪切腹板开缝，改善受力形式和破坏机制，增大腹板塑形变形区域提高耗能效率，利用有限元软件模拟分析了3个不同开缝形式的试件并找出最优开缝形式。分析结果表明该新型软钢阻尼器的滞回曲线饱满，屈服后承载力和耗能能力较其他阻尼器形式都有不同程度的提高，腹板开缝后阻尼器延性明显增大。

软钢阻尼器；防屈曲；开缝；滞回曲线

0 引言

传统耗能方法允许主结构在水平荷载作用下出现局部破坏，在地震过后对破坏部位进行修正或者替换，从而恢复结构的强度、抗侧刚度及变形能力。剪切板阻尼器(SPD)[1-2]因在地震中拥有较强的剪切变形能力、较低的花费和稳定的耗能性能被广泛应用于结构抗震设计中，且试验[3]表明采用软钢制作的金属阻尼器具有更好的低周疲劳性能。加劲阻尼器(ADAS)[4]通过一系列平行放置的钢板的面外弯曲变形来耗散能量，且纵截面采用中空设置使钢板沿截面高度同时进入屈服状态。近期Dipti Ranjan Sahoo等[5]尝试将SPD和ADAS结合提出一种弯剪型金属阻尼器(shear-and-flexural yielding metallic damper,简称SAFYD)，并试验研究该形式的破坏机制和耗能特性，试验表明在低周反复荷载作用下SAFYD腹板容易发生面外变形，从而滞回曲线出现明显捏缩。邓开来等[6]提出在SPD剪切板两侧设置加劲板(buckling restrained shear panel damper,简称BRSPD)限制钢板面外变形改善耗能性能，显著提高阻尼器延性和滞回能力。但是被限制面外变形后的剪切板容易在上下两端破坏而中间区域仅有局部塑性变形，从而耗能效率降低，故如何提高金属阻尼器耗能性能有必要进一步研究。

本文结合上述几种金属阻尼器的优点，提出了一种新型的弯剪型防屈曲软钢阻尼器(shear-and-flexural buckling restrained damper,以下简称SFBRD)，如图1所示。该金属阻尼器包括三部分：两侧X形端板，其截面宽度随高度变化，从而在承受水平荷载产生的弯矩时端板截面能同时进入塑形；中间腹板，主要承受剪力，受剪过程中腹板受力带主要发生拉伸屈服和压缩变形，为阻尼器提供主要的初始刚度；腹板两侧加劲板，约束其面外变形，提高阻尼器强度及抗侧刚度，减少由于腹板屈曲而导致的滞回性能劣化。为探讨这种新型阻尼器的减震性能，本文利用ABAQUS有限元软件对该金属阻尼器的滞回性能进行模拟分析，并同其他两类软钢阻尼器进行对比，重点讨论其滞回性能、水平承载力、抗侧刚度及耗能能力等。本文最后对腹板开缝形式做了初步探讨，以调节应力分布，改善塑形变形性能。

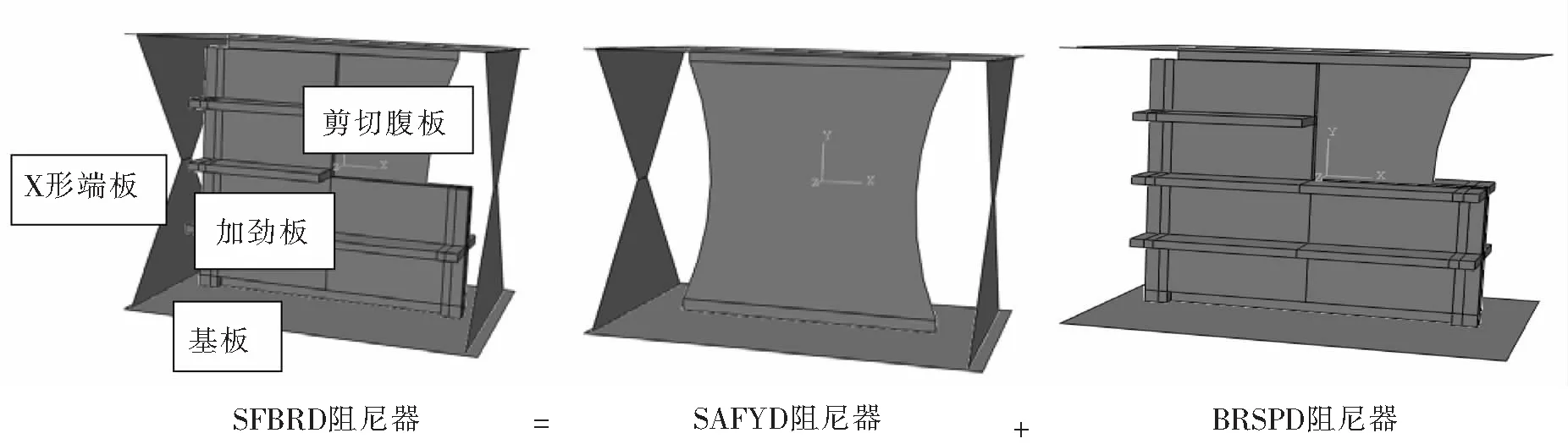
图1 软钢阻尼器模型

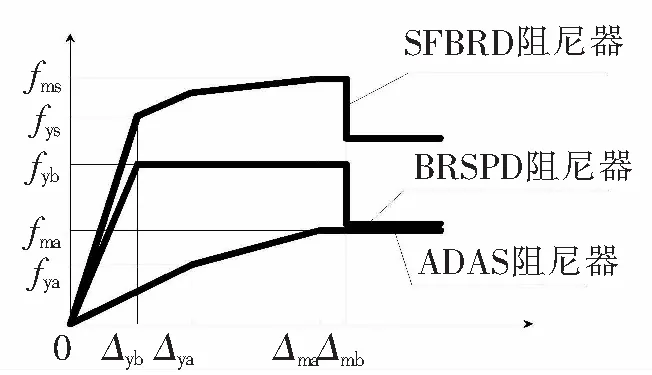
图2 水平力-位移响应模型

图2是该新型阻尼器的理论力—位移响应模型，如图所示SFBRD阻尼器可认为是在BRSPD阻尼器两边布置ADAS加劲阻尼器。BRSPD阻尼器在水平力作用下有较小的屈服位移Δyb和较大的弹性刚度，但屈服后承载力几乎没有增长；而ADAS加劲阻尼器在水平力下有较大的屈服位移Δya和较小的弹性刚度，但加劲阻尼器在平面外屈曲后还会有较大的屈曲后承载力，因而SFBRD新型阻尼器巧妙的将以上两者的优势结合在一起，提高了初始弹性刚度以及较大的屈曲后承载力fms，本文在后续分析中会进一步证实此简化假设的合理性和指导意义。

1 新型软钢阻尼器和传统软钢阻尼器的对比分析

1.1 试件设计

图3 细部尺寸(单位：mm)

为研究循环荷载作用下该新型阻尼器的耗能性能，本文共设计3个试件，分别为SFBRD、SAFYD与BRSPD阻尼器。为确保3个试件具有可比性，均采用相同的截面高度，宽度和厚度。其中SFBRD阻尼器同时布置X形端板和两侧外约束板；SAFYD阻尼器仅有X形端板而无外约束板；BRSPD阻尼器无X形端板但有外约束板。剪切腹板厚6 mm，两侧边采取圆弧形设计；X形端板厚10 mm，中间截面宽30 mm；腹板与两侧约束板间有1 mm间距，且约束板外侧各有3道横向加劲肋。试件具体尺寸如图3所示。

1.2 有限元模型的建立

首先，为确保数值模拟的可靠性及合理性，采用非线性有限元软件ABAQUS6.11对文献[6]中防屈曲剪切板阻尼器试验试件S1进行了有限元模拟验证，该实验试件S1有限元模型如图1中BRSPD阻尼器所示。试验软钢腹板材料为LY225，加劲板采用Q235钢材。有限元建模处理如下：高强螺栓部分采用简化处理，不考虑螺栓力；剪切腹板采用壳单元，外约束加劲板采用实体单元建模，网格尺寸取10 mm；剪切腹板和外约束板之间法向作用采用“硬接触”模拟，腹板与加劲板间切向作用同原文献中取摩擦系数0.3;约束阻尼器下基板所有自由度，即下基板与地面固接，约束阻尼器上基板面外和竖向位移，对上基板施加水平侧向位移；Q235钢材本构关系采用原文献中数据，屈服强度为297 MPa，极限强度为484 MPa，对应的极限应变为0.15。材料LY225本构关系采用和文献[6]中一样的混合强化法则，本次有限元验证所使用材料强化参数采用文献[6]中已有的数据，如表1所示。

表1 材料强化参数 MPa

图4 实验结果和有限元结果的比较

现有研究表明[7]ABAQUS软件中的材料混合强化法则能较好的模拟LY225具有的循环强化特征，该强化法则包含了等向强化和随动强化两部分，其中随动强化部分采用多个背应力叠加的方式，可以提高材性拟合的准确度。其中，σ0为零塑性应变时的应力，Ck为第k个(k=1,2,3,4)背应力时的最大变化值，γk为第k个背应力随塑性应变增加的变化率。文献[7]中试件S1试验结果和数值模拟结果如图4所示，可以看出有限元模拟较好地预测了试件在低周循环荷载下的弹塑性行为，试件在位移达到20 mm时水平承载力都达到了300 kN，这说明本文所采用的有限元简化模型基本正确，分析结果较为可靠，而且所采用的材料本构关系也较为适用。

本文在确定数值模拟的有效性后，利用ABAQUS软件建立SFBRD、SAFYD与BRSPD阻尼器3个试件的模型，剪切腹板、X形端板采用壳单元，外约束加劲板采用实体单元建模，网格尺寸取10 mm。本文中剪切腹板和外约束板之间采用“硬接触”，假设腹板与加劲板间无摩擦。腹板和端板材料均采用低屈服点钢材LY225，弹性模量E=2.06×105MPa，泊松比ν=0.3，混合强化参数采用表2数据。X形端板和加劲板采用Q235钢材，材料本构关系同上面验证数据。由钢结构设计规范建议，采用位移加载方式，加载点位于基板顶侧面。为提高计算效率，循环加载按Δy、2Δy、4Δy、6Δy、8Δy…的方式进行(Δy为结构的显著屈服位移)，超过2Δy位移幅值每级荷载循环2次，直至试件承载力降至峰值荷载的85%。在有限元模型中约束了基板底节点所有方向的自由度，基板顶约束面外位移和竖向位移，有限元模型如图1所示。

1.3 循环荷载作用下的P-Δ滞回曲线

根据ABAQUS对3个试件在单调荷载作用下的模拟分析得到各试件的显著屈服位移Δy，均在2.5 mm左右。3个试件在循环荷载作用下各加载至8Δy，其中试件SFBRD和BRSPD在位移8Δy时仅加载一个循环，承载力就降至峰值荷载的85%，停止加载。3个试件的P-Δ滞回曲线(水平力-侧移曲线)如图5所示。

图5 P-Δ滞回曲线

由图5可以得出：试件SFBRD和BRSPD的滞回曲线基本呈矩形，且试件SFBRD的滞回曲线能包住试件BRSPD的滞回曲线，试件破坏前水平承载力持续上升，有更大的水平承载力；试件SAFYD由于加载过程中腹板有较大的面外屈曲，滞回曲线有明显捏缩。加载至8Δy级位移20 mm时，3个试件均出现不同程度的破坏，承载力降低，停止加载。此外，试件SFBRD的滞回曲线也验证了图2中理论模型的合理性。

1.4 骨架曲线

3个试件的骨架曲线如图6所示，骨架曲线可以反映出软钢阻尼器的刚度、承载力和延性。

表2 试件承载能力、位移及延性系数

由图6可知，加载后期，SFBRD试件的最大承载力和刚度均比试件BRSPD和SAFYD的大。表2给出了试件各特征点的承载力值、侧移及延性系数。表中fy、Δy、fmax、Δmax、fu、Δu、μ分别为屈服荷载、屈服位移、峰值荷载、峰值位移、极限荷载、极限位移和延性系数，其中位移延性系数μ为结构极限位移与结构屈服位移的比值，即Δu/Δy，它是衡量结构塑形变形能力和抗震性能的重要指标。屈服位移根据工程力学法[8]建议的方法确定，极限位移取荷载下降至峰值荷载85%或结构破坏所对应的位移。由表2可知，3个试件的位移延性系数接近，均大于4，说明3个试件延性均较好。

1.5 刚度退化分析

试件抗侧移刚度的退化过程反映了试件在低周循环荷载下的刚度退化性能，本文在分析刚度退化时采用割线刚度K来描述,割线刚度用式(1)计算。式中，f+、f-是试件在同一滞回环峰值点的正、负向水平荷载；Δ+、Δ-是同一滞回环在峰值点的正、负向水平位移。

(1)

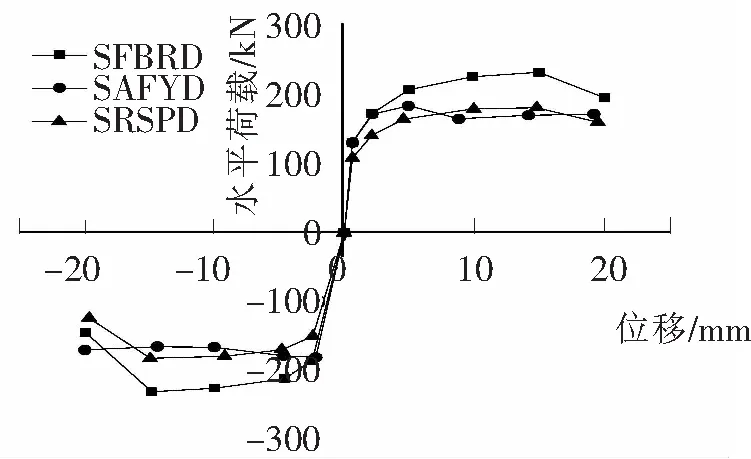
图6 试件的骨架曲线

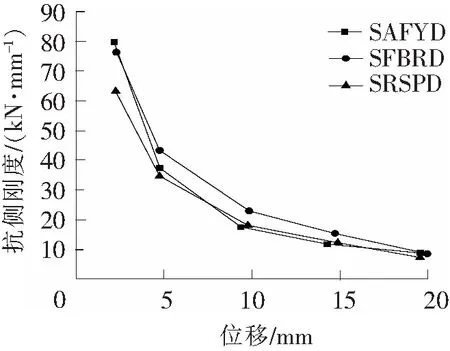
图7 刚度退化曲线

两试件的刚度退化曲线如图7所示，图7中横坐标为同一滞回环峰值点的正负向位移绝对值的平均值。总体上看，试件SAFYD和BRSPD的刚度低于试件SFBRD。加载前期，各试件基本处于弹性或小变形状态，此时试件SAFYD和SFBRD的刚度基本相同，且略均大于试件BRSPD；随着加载级的增大，试件SAFYD腹板出现面外屈曲而抗侧刚度迅速减小，试件BRSPD由于腹板上下两端率先进入塑性阶段因而刚度有一定的下降，而试件SFBRD因为两侧抗弯端板分担了水平荷载下腹板两端的弯矩，减小了腹板的塑形变形，这在一定程度上增加了试件SFBRD的抗侧刚度。3个试件的刚度退化曲线对比说明两端X形端板和腹板外约束加劲板均减缓了该阻尼器刚度退化的速度。

1.6 耗能能力分析

滞回环的饱满程度反映了试件的耗能能力，采用滞回环包围的面积作为耗散的能量E。JGJ101—96《建筑抗震试验方法规程》[9]指出能量耗散能力可采用能量耗散系数He来判别，试件的能量耗散系数根据P-Δ滞回曲线的包络线(如图8所示)来确定，采用式(2)计算，He越大，表明试件的耗能能力越强。

(2)

由于试件失效前各进行5级加载循环，3个试件均采用前5级加载循环的耗能系数进行对比分析。各加载级的耗散能量和能量耗散系数变化分别如图9和10所示。由图9可知，3个试件耗散的能量均随着加载级增大而增大，其中试件SFBRD和BRSPD耗散的能量有较为显著的增长，而试件SAFYD由于加载过程中腹板面外屈曲，能量耗散能力较弱。而图10中随着加载级的增大，SFBRD和BRSPD阻尼器的耗能系数均得到了增长，加载后期随着阻尼器的破坏，耗能能力减弱。SFBRD阻尼器在加载过程中两侧X端板仅有中间区域进入塑性状态，所以SFBRD阻尼器相比BRSPD阻尼器的耗能系数较小。SAFYD阻尼器在加载初期面外屈曲不明显，耗能系数有一定增长，后期随着面外变形的加大，每个加载位移级的耗散能量增长幅度较小，耗能系数逐渐下降。由上述分析可知，腹板外约束加劲板明显增强了软钢阻尼器的耗能能力。

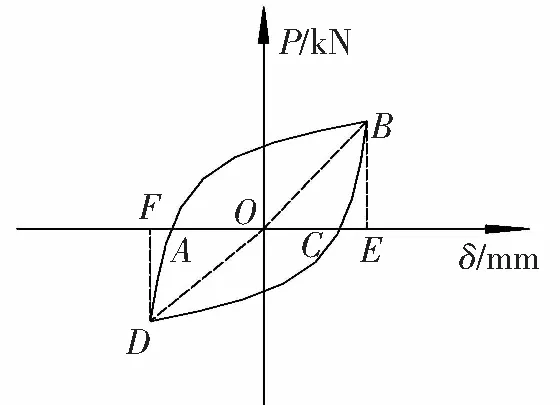
图8 包络线图

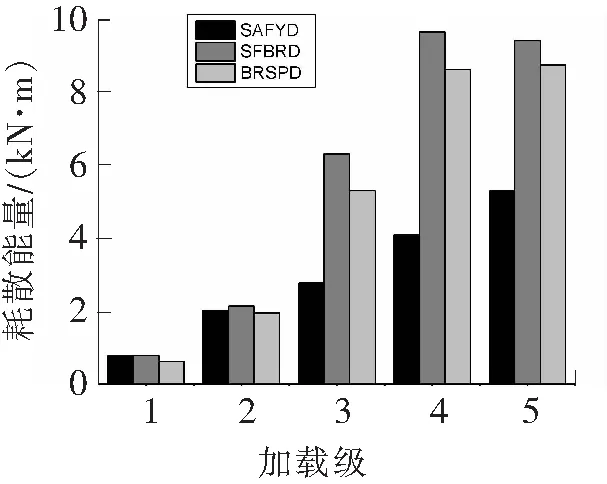
图9 耗散能量E

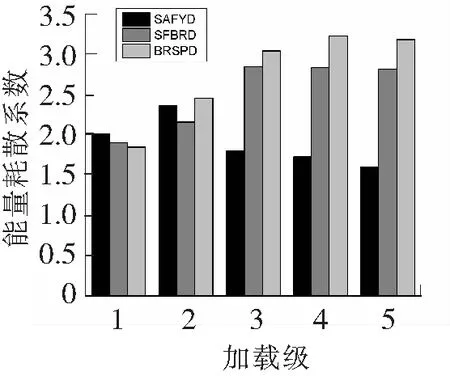
图10 能量耗散系数He

2 开缝形式对该SFBRD软钢阻尼器滞回性能的影响

从以上分析可知，试件SFBRD和BRSPD相比试件SAFYD的延性偏低，加载位移在达到20 mm时承载力下降较快，这是因为受剪腹板上下两端发生明显破坏而导致承载力下降，而腹板中间区域塑形变形并不明显，局部区域还处在小变形阶段，材料利用率不高。本文参考现有研究成果[10-11]，尝试对SFBRD软钢阻尼器腹板开缝使腹板均匀受力，最大化提高材料利用率和阻尼器延性性能，提出如图11所示的3种开缝形式，以找出最优开缝方法。如图所示，试件S1在腹板中间区域开缝，缝隙高均为80 mm，宽1 mm，试件S2和S3在腹板上下两侧开缝，开缝宽均为1 mm，试件S2开缝高度均为80 mm，而试件S3为由外向内开缝高度逐渐变小，最小开缝高度为40 mm。有限元分析可知，腹板开缝后试件加载过程中腹板面外变形较小，破坏首先发生在缝隙两端，之后向周围区域扩散，这样渐进破坏能充分利用腹板材料，提高能量耗散程度。

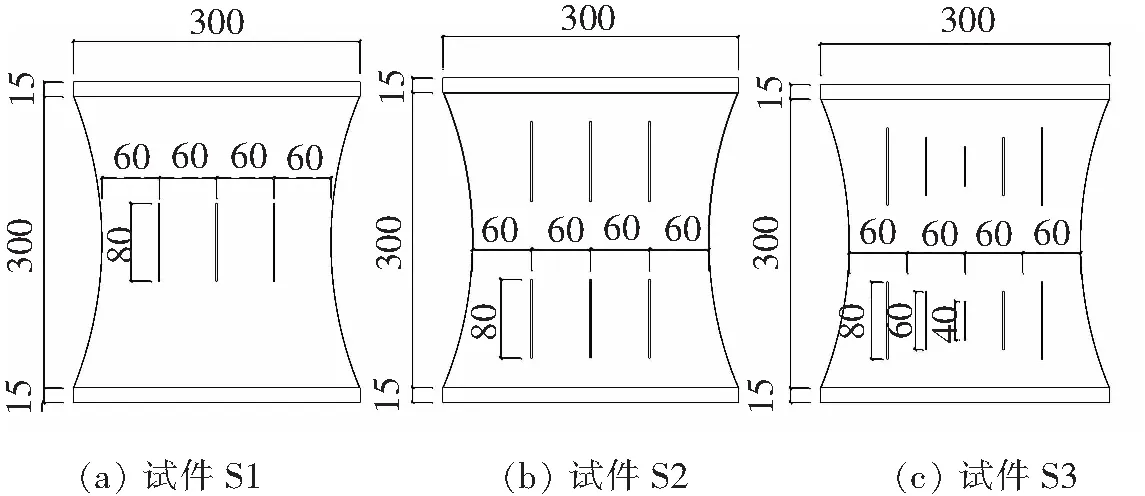
图11 3个试件开缝形式(单位：mm)

图12 不同开缝形式下试件滞回曲线的对比

3个试件S1、S2、S3在低周循环加载下的滞回曲线如图12所示，表3给出了3个开缝试件与标准试件SFBRD各特征点的承载力值、侧移及延性系数。由图12和表3可知：(1)腹板开缝后承载力有一定程度下降，承载力在达到25 mm时才有较明显的下降，显著增大了阻尼器延性；(2)试件S3的滞回曲线能完全包裹住S1和S2的滞回曲线，3个试件在加载初期滞回曲线基本重合，后期S1和S2承载力下降明显，而S3依然保持较高承载力和耗能能力，这是由于腹板开缝后在位移加载过程中竖缝两端率先破坏，然后破坏区域向周围扩散，而试件S3因错开破坏区域，受力性能得以改善，充分利用钢板材料，显著增大试件延性，说明试件S3的开缝形式较为合理高效。

表3 腹板开缝后试件承载能力、位移及延性系数结果

3 结论

(1)本文提出一种新型弯剪型防屈曲软钢阻尼器，有限元数值分析表明该新型阻尼器的滞回曲线比较饱满，结构耗能能力较好。

(2)该新型软钢阻尼器的抗侧刚度和屈曲后承载力相比弯剪型软钢阻尼器和防屈曲软钢阻尼器更大，且延性相差不大，两端X形板和腹板外约束加劲板的存在有效延缓了该阻尼器的刚度退化速度。

(3)新型软钢阻尼器和防屈曲软钢阻尼器的能量耗散系数基本接近，弯剪型软钢阻尼器由于腹板面外屈曲变形而耗能系数较低，耗能能力较弱。

(4)对新型软钢阻尼器腹板开缝，能有效调节腹板应力分布，增大材料利用率，避免腹板上下两端过早破坏，显著提高阻尼器延性性能，且缝高由外向内逐渐变小的开缝形式受力性能最好，延性最大。

[1]Tanaka K,Sasaki Y.Hysteretic performance of shear panel dampers of ultra-low-yield-strength steel for seismic response control of buildings[C]//12th World conference on Earthquake Engineering.New Zealand:WCEE,2000:1-8.

[2]Chan RWK,Albermani F,Williams MS.Evaluation of yielding shear panel device for passive energy dissipation[J].J Construct steel Res,2009,65(2):260-268.

[3]Nakashima M.Strain-hardening behavior of shear panels made of low-yield steel[J].J Struct Eng,1995,121(12):1742-9.

[4]C.Xia,R.D.Hanson,Influence of ADAS element parameters on building seismic response[J].ASCE.Struct.Eng.，1992,118(7):1903-1918.

[5]Dipti Ranjan Sahoo,Tarun Singhal,et al.Cyclic behavior of shear-and-flexural yielding metallic dampers[J].J Construct steel Res,2015,114:247-257.

[6]Kailai Deng,Peng Pan.Development of a buckling restrained shear panel damper[J].J Construct steel Res,2015,106:311-321.

[7]石永久，王佼姣.循环荷载下低屈服点钢材LYP225的力学性能[J]. 东南大学学报，2014,44(6)：1260-1265.

[8]中国科学院工程力学研究所.地震工程研究报告集(第三卷)[M]. 北京: 科学出版社, 1977.

[9]中国建筑科学研究院.JGJ 101—96 建筑抗震试验方法规程[S]. 北京：中国计划出版社，1997.

[10]马良.带竖缝钢板剪力墙受力性能分析[D].大庆：东北石油大学，2014.

[11]郑杰，李爱群.竖缝式墙型阻尼器力学性能及减震性能研究[J].华中科技大学学报，2014,42(1)：73-77.

The Hysteretic Behavior Research of a New Flexural-and-shearBuckling-Restrained Mild Steel Damper

Zheng Hong, Quan Kai, Ding Shuangjie

(School of Civil Engineering，Chang’an University，Xi’an 710061，China)

The energy dissipation potential of a metallic damper largely depends on the inelastic deformation and the hysteretic response of the energy elements under either axial or flexural or shear loading. In this study, a new type of mild steel damper called a shear-and-flexural buckling-restrained damper is proposed, which consists of three main parts, two end plates of X-configuration allowed to yield under flexural action, a mild steel web mainly subjected to shear loading, and two pieces of restraining steel plate with stiffener clamping the energy dissipation plate to prevent out-of-plane bucking. In this paper the three specimens of different damper are compared and analyzed using ABAQUS, which mainly focus on setting, or not setting, of the buckling plate and end plates of X-configuration. In order to further study the optimization of the new damper, the shear web is slotted to improve force form and failure mechanism, and increase the plastic deformation region to improve energy efficiency of the web, three specimens of different slot forms are analyzed using finite element software to find the optimal slot form. The results show that the new type of mild steel damper has full hysteretic curve, and the post yield bearing capacity and energy dissipation capacity are improved in different degrees compared with other structural forms, and the ductility increases obvious when the web is slotted.

mild steel damper;buckling-restrained;slot;hysteretic curve

郑宏(1964-),男,博士,教授，研究方向为钢结构的研究。E-mail:73460669@qq.com

TU39

A

2095-0373(2017)02-0011-07

2016-03-22 责任编辑:刘宪福

10.13319/j.cnki.sjztddxxbzrb.2017.02.03

郑宏,全凯,丁双杰.新型弯剪型防屈曲软钢阻尼器的滞回性能研究[J].石家庄铁道大学学报:自然科学版,2017,30(2):11-16.