混凝土简支梁在均布荷载作用下的断裂过程区及自振特性

郭全民, 段树金

(1.石家庄铁道大学 土木工程学院，河北 石家庄 050043;2.铁四院(湖北)工程监理咨询有限公司，湖北 武汉 430000)

混凝土简支梁在均布荷载作用下的断裂过程区及自振特性

郭全民1,2, 段树金1

(1.石家庄铁道大学 土木工程学院，河北 石家庄 050043;2.铁四院(湖北)工程监理咨询有限公司，湖北 武汉 430000)

以“段-中川模型”为基础，叠加几种无限大体和半无限大体的弹性力学问题解答，用选点法近似满足边界条件，推导出了均布荷载作用下含断裂过程区混凝土简支梁的应力函数全场解析解；由能量法得到了梁的自振频率，分析了裂缝长度和断裂过程区长度对自振频率的影响；将断裂过程区的长度用节点非线性弹簧表示，采用Ansys软件数值模型模拟了带断裂过程区的混凝土简支梁，得到混凝土简支梁典型截面的应力分布、竖向位移、裂缝张开位移和自振频率。理论计算结果和仿真分析结果吻合较好。

混凝土梁；断裂过程区；应力函数；位移函数；拉应变软化曲线；自振频率

0 引言

Westergaard[1]给出均匀拉力作用下中心裂纹无限大均质板问题的应力函数，其解答简洁明了，成为线弹性断裂力学的基础。其裂纹尖端的应力呈无穷大，张开位移呈椭圆形，在很多情况下与实际存在差异。研究表明，以混凝土为代表的准脆性材料与金属材料不同，裂缝尖端区域具有较大的断裂过程区，用线弹性断裂力学解决混凝土等准脆性材料的断裂问题显然是不合适的。虚裂缝模型[2]能够较好的反应混凝土在外力作用下的受力和变形特点，但很难得到虚裂缝模型的解析解。推导基于虚裂缝模型的解析解具有重大的理论和实践意义。

段、中川等[3-4]以弹性理论为基础，采用加权积分法成功得到了拉力作用下中心裂纹的无限大板和含裂缝4点弯曲简支梁的断裂过程区内黏聚应力和张开位移并存的解析解。

本文通过加权积分后应力函数的叠加，得到均布荷载作用下含断裂过程区混凝土简支梁的应力函数，并根据能量法计算梁的自振频率。

1 问题的应力函数

1.1 弹性力学问题的复变函数表示

对于弹性力学平面问题，应力函数可用以下复数的形式表示

(1)

相应的应力和位移分量可以表示为

(2)

(3)

式中，G为剪切模量，平面应力时κ=(3-v)/(1+v)，平面应变时κ=3-4v，v为泊松比。

1.2 一些基本问题的应力函数

(1)弯矩作用下带对称边裂缝的无限大板。

带对称裂缝的无限大板无穷远处受弯矩作用，如图1所示，其弹性解答为

(4)

(5)

采用加权函数法，消除解的奇异性，加权函数采用三角加权函数ρ=2(a+b-t)/b2, 经过加权积分的弹性解答为

(6)

(7)

(8)

(9)

(2)均布荷载作用下简支梁。

均布荷载作用下的简支梁，如图2所示，其应力分量可用复变函数表示为

(10)

(11)

图1 弯矩作用下无限大板

图2 均布荷载作用下简支梁

1.3 叠加法求问题的应力函数

图3所示的平面问题，可以通过叠加上节的基本应力函数得到图4所示带断裂过程区梁模型的全场解析解，应满足的边界条件如下。

(1) 梁的有效高度为韧带长度和断裂过程区长度之和a+b。

(2) 裂缝尖端y=a处正应力达到抗拉强度ft, 即Σσa=ft时，裂缝向前扩展，并始终沿y轴方向。

(3) 梁截面有效高度范围内应力合力为零，即ΣT1j=0。

(4) 梁端弯矩和正应力合力为零，即ΣMj=0,ΣT2j=0；梁底一半的正应力和切应力的合力为零，即ΣT3j=0,ΣQj=0。

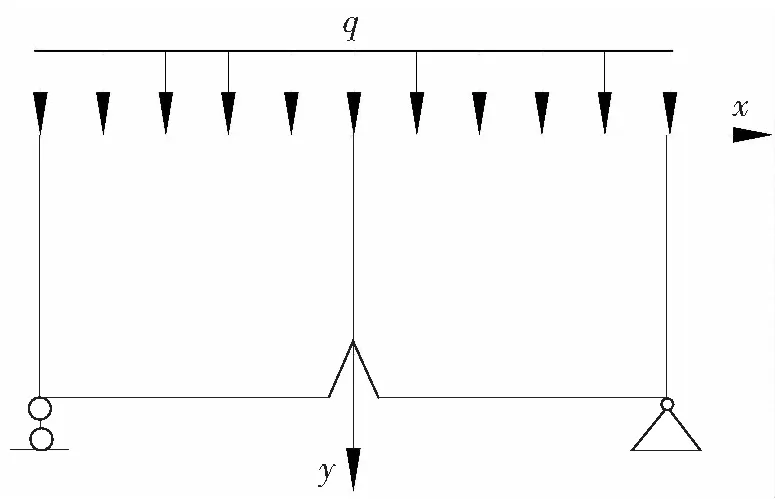
图3 均布荷载作用下带裂缝简支梁

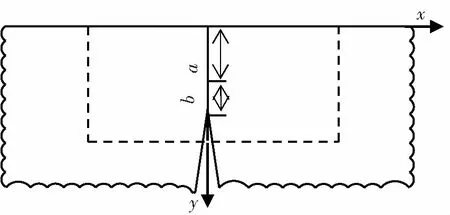
图4 本文研究的裂缝模型

基于以上假设，方程可用矩阵表示为

(12)

由此可以得到Xi，即各基本函数在解中的权重，根据解答得到的权重，即可通过叠加得到带裂纹简支梁的应力函数、挠度函数和裂纹的张开位移函数。

1.4 梁的自振频率

基于以上得到的简支梁在均布荷载作用下的应力函数和位移函数，将梁的质量等效为均布荷载，即可由以下公式计算含切口断裂过程区简支梁的第一自振频率，

(13)

式中，Y(x)为梁的竖向位移函数。

1.5 算例

一混凝土简支梁，高度H=8 cm，宽度B=7.5 cm，长度L=30 cm，裂缝长度1 cm，混凝土抗拉强度ft=5.6 MPa，泊松比v=0.2，弹性模量E=28 GPa。

由应力函数得到的沿断裂韧带正应力分布如图5所示，从图5可以看出，应力奇异性消失，应力最大值出现在断裂过程区尖端处，同时满足正应力的合力为零的条件；真实裂纹面上的正应力不为零是误差所致。

断裂过程区张开位移曲线如图6所示，尖端呈闭合形状。

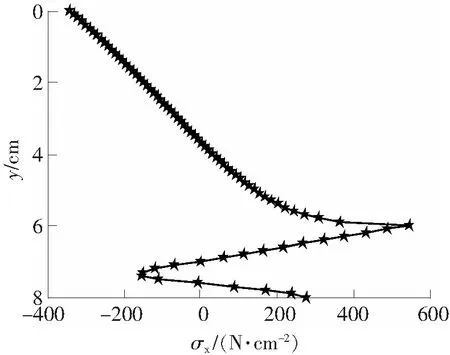
图5 沿断裂韧带σx分布

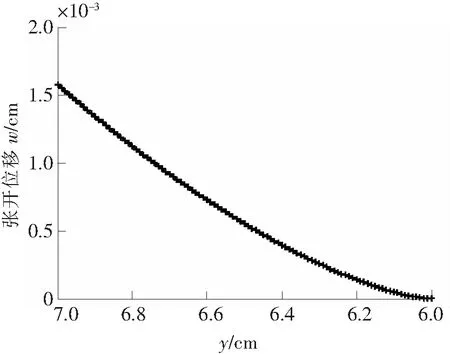
图6 断裂过程区张开位移曲线

根据图5和图6，得到的拉应变软化曲线如图7所示。

将挠度拟合成四次曲线，由式(12)得梁自振频率ω=0.101 Hz。

假设断裂过程区尺度b=1.0 cm，裂缝长度与自振频率的关系如图8所示，从图8中可以看出，随着裂缝深度的增长，自振频率呈非线性的减小，非线性特点明显。

图7 拉应变软化曲线

图8 韧带尺度与自振频率关系曲线(b=1 cm)

2 有限元仿真分析

运用Ansys软件建立了仿真模型，仿真模型中包含了裂缝和断裂过程区，断裂过程区用弹簧模拟，弹簧刚度由计算所得。混凝土简支梁受均布荷载，端部施加铰约束，施加在梁端高度的一半的位置附近，混凝土模型采用plan42单元，断裂过程区的弹簧用combin14单元，设置为轴向受力弹簧，混凝土简支梁的单元厚度取单位厚度，单元为0.1 cm×0.1 cm的四边形单元,整个模型共分为24 140个单元。

将断裂过程区的长度b平均分成n等份，每段的长度h=b/n，同时假设每一小段上的应力分布呈直线分布，但斜率不同，从而得到第i段上的应力的合力为

(14)

从而根据胡克定律可以计算出第i节点上的弹簧刚度如下

(15)

断裂过程区张开位移呈曲线形状，本文用折线代替曲线，采用5个弹簧模拟，弹簧从上到下的编号为1,2,3,4,5，根据应力和水平位移计算出弹簧的刚度值如表1所示。

表1 断裂过程区弹簧刚度 N/mm

图9 沿断裂韧带理论计算与仿真分析正应力分布的比较

仿真分析得到的混凝土简支梁的最大挠度为0.004 548 cm，频率为0.098 222 Hz。

将理论计算出的裂缝及其延长线上的正应力分布与仿真分析的结果进行比较，如图9所示，二者吻合良好。

3 结论

通过以上研究发现，得出了如下的结论：

(1)基于Duan-Nakagawa模型，得到了含断裂过程区的混凝土简支梁的全场解析解，根据应力函数计算出裂纹及其延长线上应力符合虚裂纹模型的应力分布，应力边界条件基本满足。

(2)理论计算方法得到了裂纹张开位移曲线和软化曲线，张开位移曲线在裂纹尖端呈缓慢收缩于零的闭合形状，软化曲线整体上是一条下凹的曲线，开始随应力降低，位移减小较快，到达裂纹尖端附近位置，位移缓慢收缩至零。

(3)含裂缝梁的韧带长度对梁的自振频率影响大，随着韧带长度减小，自振频率降低较快，明显呈非线性；而断裂过程区长度对结构自身频率的影响较小。

[1]WESTERGAARD H M. Bearing pressures and crack[J]. J.Applied Mech. Transactions of the ASM, 1939, 33(A):49-53.

[2]HILLERBORG A. Analysis of fracture by means of the fictitious crack model.particularly for fiber-reinforced concrete[J]. Int J Cement Compos, 1980(2):177-188.

[3]DUAN S J, NAKAGAWA K. Stress functions with finite stress concentration at the crack tips for central cracked panel[J], Engng Fracture Mech., 1988, 29(5):517-526.

[4]DUAN SHU JIN, NAKAGAWA K. A mathematical approach of fracture macromechanics for strain-softening material[J]. Engineering Fracture Mechanics, 1989(34):1175-1182.

Fracture Process Zone and Natural Vibration Characteristics ofConcrete Beam Under Uniform Distributed Forces

Guo Quanmin1，2, Duan Shujin1

(1.School of Civil Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043, China;2.China Railway Siyuan (Hubei) Engineering Supervision Consulting Co.,Ltd , Wuhan 430000, China)

The analytical solution of a simply supported beam under uniform distributed force with a fracture process zone is deduced based on the “Duan-Nakagawa's model” by superposition of several solutions of elastic mechanics problems, and its natural vibration frequency is calculated based on the energy method. The influence of crack length and fracture process zone length on the natural frequency is analyzed. The FEA software ANSYS is used to simulate the fracture process for a simply supported concrete beam, in which, the cohesive forces in the fracture process zone are represented by the nonlinear springs. The stress distribution, the vertical displacement, the crack opening displacement, and the natural vibration frequency of the beam are demonstrated, which are in good agreement with the theoretical calculation.

concrete beam；fracture process zone；stress function；displacement function；tensile strain softening curve；natural vibration frequency

2016-05-20 责任编辑:刘宪福

10.13319/j.cnki.sjztddxxbzrb.2017.02.02

河北省自然科学基金(A2015210029)，河北省高等学校科学技术研究重点项目(ZH2012040)

郭全民(1987-),男,硕士,助理工程师,研究方向为桥梁与结构工程。E-mail：247524924@qq.com

TU375.1

A

2095-0373(2017)02-0006-05

郭全民,段树金.混凝土简支梁在均布荷载作用下的断裂过程区及自振特性[J].石家庄铁道大学学报:自然科学版,2017,30(2):6-10.