李超代数gl(1，2)型心与拟型心的矩阵表示*

张洪娟，李明明，郑克礼

(东北林业大学)

李超代数gl(1，2)型心与拟型心的矩阵表示*

张洪娟，李明明，郑克礼＊＊

(东北林业大学)

讨论一般线性李超代数一类子代数gl(1，2)的型心与拟型心.应用解方程组的方法完全确定此类李超代数的型心和拟型心的矩阵表示.

型心;拟型心;矩阵表示

0 引言

一般来说，在环理论中作为一个局部环来研究不可分解李代数的型心极其困难，因此关于非单李代数的型心很少有更深入详细的研究［1］.在文献［2］中Duncan J.Melville探讨了一些与单李代数或仿射李代数相关的幂零李代数及其类似的无限维代数的型心问题.作为李代数自然推广的李超代数，不仅紧密依赖于李代数，而且在核物理，超引力等方面起着重大作用.Ronald Skurnick在文献［3］中采用了新的方法证明Jordan的型心定理.2003年河北大学张智学教授等在文献［4］中得到了单李超代数的超型心都是超域，并且得到了单李超代数的零次型心与Killing型之间的关系.而拟型心的元素是特殊的广义导子，在文献［5］中给出了拟型心保持诣零根结论的李超代数推广.文献［6］为了研究一类李代数的导子推广，研究并给出了这类特殊李代数的型心和拟型心的许多性质.历经几十年的研究，李超代数的型心已经取得了许多进展，但总的来说还处在发展时期，许多重要问题有待解决.

由型心和拟型心的定义可知它们都是线性空间上的线性变换.因此如果能找出gl(1，2)的一组标准基，就可以应用gl(1，2)本身的李乘运算并根据型心和拟型心的定义列出线性方程组.之后再通过系数比较法得出系数值，并得到矩阵中的元素.最后用代数表达式写出矩阵表示的简化形式.该文结构如下:第一个部分是预备知识，介绍了该文需要用到的关于李超代数gl(1，2)以及型心和拟型心的概念及简单性质.第二个部分是主要内容，其中叙述了有关［，］运算的规律以及拟型心和型心的矩阵表示法.

1 预备知识

令该文的基域为复数域.

定义1.1设是李超代数，

则Γ(A)={f∈End(A)|f［x，y］=［f(x)，y］=(－1)d(x)d(f)［x，f(y)］，x，y∈A}为A的型心.

QΓ(A)={f∈End(A)|［f(x)，y］= (－1)d(x)d(f)［x，f(y)］，x，y∈A}为A的拟型心.

令eij=(δij)3×3，i，j=1，2，3为gl(1，2)一组标准基，其中δij为Kronecker符号，基在f作用下为:

命题1.1设f是gl(1，2)上的线性变换，则在基eij(i，j=1，2，3)上的矩阵表示式如下:

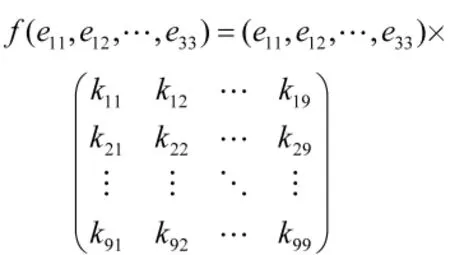
当f表示型心作用下的线性变换时，由元素kij组成的矩阵即是型心矩阵表示法.当f表示拟型心作用下的线性变换时，由元素kij组成的矩阵即是拟型心矩阵表示法.

2 主要结论

定义2.1设是域F上的Z－阶化超代数，对任意的j∈z，x∈Lj，称x是L的j次齐次元，记deg x=j.

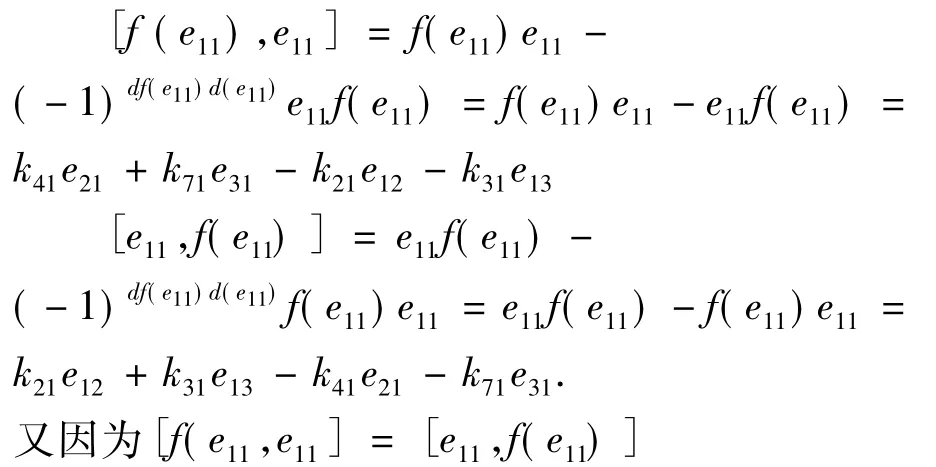
所以通过比较系数得:

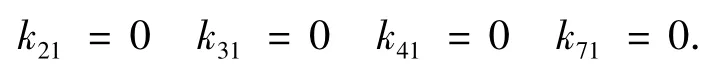
其他情况同理可得:

因此可得以下定理.

定理2.1设f偶变换，则gl(1，2)的拟型心矩阵为:

其中a，b，c，d，e，f，g，h，i，λ为任意的复数.

证明由定义2.1及拟型心的定义可得.

定理2.2设f是奇变换，则gl(1，2)的拟型心矩阵为:

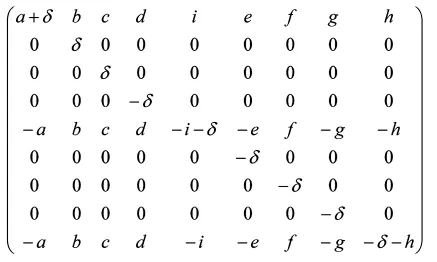
其中a，b，c，d，e，f，g，h，i，δ为任意的复数.

设f是偶变换，根据型心的定义，同样eij(i，j=1，2，3)代替定义中的x，y，当x=e11且y=e12时，有:

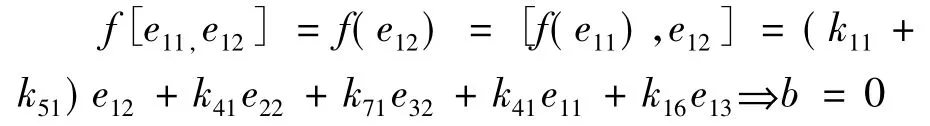
其他情况同理可得:b=c=d=e=f=g=0，i=h=－a

因此，有以下定理.

定理2.3设f是偶变换，则gl(12)的型心矩阵为:

其中a，λ为任意的复数.

同理，根据f为奇变换定义运算可得:

定理2.4设f是奇变换，则gl(1，2)的型心矩阵为:

其中a，δ为任意的复数.

［1］Kac V G.Classification of Infinife－dimensional Simple Linearly Compact Lie Superalgebras［J］.Adv Math，1998，139 (1):1－55.

［2］Melvile D J.Centroids of Nilpotent Lie Algebras.Comm Algebra，1992，20(12):3649－3682.

［3］Ronald S，Li G Y.A New Proof of Jordan’s Centroid Theorem.华南师范大学学报:自然科学版，1999(2):6－9.

［4］Zhang Z X，Liu L Q.The Centriod of Lie Superalgebras.J Hebei University Natural Science Edition，2003，23(1):85－87.

［5］李明珠.李超代数拟型心的型心的性质.哈尔滨师范大学:自然科学学报，2010，26(3):28－30.

［6］Abdeljelil A B，Elhamdadi M，Makhlouf A.Derivations of ternaty Lie algebras and generalizations.Int Electron J Algebra，2017(21):55－75.

A Matrix Representation of Centroids and Quasicentroids for Lie Superalgebras gl(1，2)

Zhang Hongjuan，Li Mingming，Zheng Keli

(Northeast Forestry University)

In this article，the centroids and quasicentroids of a class of subalgebras of the general linear Lie superalgebras gl(1，2)are mainly discussed.By the method of solving the system of equations，the matrix representation of centroids and quasiccentroids for this class of Lie superalgebras are determined.

Centroid;Quasicentroid;Matrix representation

O152.5

:A

:1000－5617(2017)01－0001－03

(责任编辑:季春阳)

2016－12－11

*黑龙江省东北林业大学大学生创新项目(201610225243);国家自然科学基金资助(11626056，11471090)

＊＊通讯作者