氧化锌的拉曼频移—应力定量关系研究

刘 武，赵华成，项 春，卢孔宝

(1.浙江水利水电学院 机械与汽车工程学院，浙江 杭州 310018；2.浙江水利水电学院 工程实验实训中心，浙江 杭州 310018)

氧化锌的拉曼频移—应力定量关系研究

刘 武1，赵华成2，项 春1，卢孔宝1

(1.浙江水利水电学院 机械与汽车工程学院，浙江 杭州 310018；2.浙江水利水电学院 工程实验实训中心，浙江 杭州 310018)

在MEMS器件制备过程中，对微区域的应力状态测量与监控至关重要.建立了氧化锌材料的拉曼应力测量技术理论，推导出了氧化锌材料的拉曼频移-应力分量解析关系式.ZnO单晶体属于6 mm点群结构具有两个A1、E1和E2共六中线性振动模式.从微扰势出发并结合胡克定律出发，推导出了A1、E1和E2模的拉曼位移变化与应力分量之间的关系，在这些方程式中，共包含20个未知参数.最后给出了氧化锌材料的拉曼频移-应力关系式，为ZnO残余应力测量提供理论依据.

氧化锌；拉曼频移；应力

近年来，随着纳米/微米级的微结构材料不断开发，对微结构应力状态的把握已经成为不可缺少的技术.目前，作为应力测定法被广泛采用的X线衍射法虽然是一种以金属及陶瓷等多种物质为测定对象[1]，通用性较高的有效手法，但测定领域仅为数10μm，对于微结构物质的应用存在着极限.另一方面，作为超微领域的应变测定法，还可采用透射型电子显微镜(TEM)的聚集电子束衍射(CBED)法[2-3].采用TEM虽然可以测定数纳米级别，试片需要薄片化到100nm以下，则会使应力被释放，形成与实际材料实际应力状态不同.与此相对，显微拉曼光谱法虽然测定对象物质仅限硅及氧化锌等拉曼活性材料，但通过非破坏、非接触方式，可在亚微米空间分辨率下完成对应力的测定.作为采用该显微拉曼光谱法测定的事例，例如对硅晶片的应变/应力测定[4].这种情况下,被测定应变是假定为一轴或等二轴的应力测定[5-6],几乎没有对实际应变及实际应力成分进行定量测定的事例.另外，作为对陶瓷的应力测定事例，报告有对石英及蓝宝石的应力测定.这些都与硅同样，均为一轴应力下的测定及对单向应力成分的同定，而对总应变成分及总应力成分进行同定的事例一概没有.因此，在本研究中，采用显微拉曼光谱法进行了亚微米空间分辨率下，对氧化锌材料的拉曼频移—应力关系式进行研究.

1 材料及应变测量理论

1.1 材料

本实验采用了氧化锌(纤锌矿)，其结构属于6 mm点群，具有2A1+2B+2E1+2E2八个声子振动模式，其中具有拉曼活性的振动模式为2A1、2E1、2E2，其拉曼光谱(见图1).光谱峰值，A1振动模式下为378 cm-1、579 cm-1，E1振动模式下为407 cm-1、590 cm-1，E2振动模式下为99 cm-1、437 cm-1，共计6个峰值存在.另外，如果将氧化锌的各振动模式用拉曼张量的形式表示为以下公式[5]：

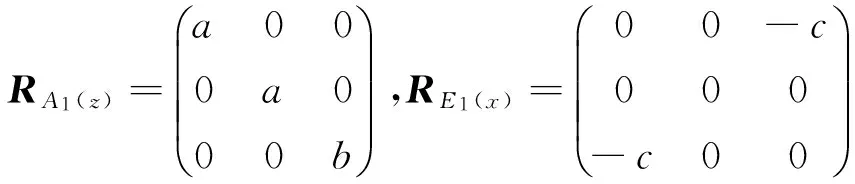
(1)

图1 氧化锌拉曼光谱图

1.2 坐标系定义

拉曼光谱坐标系(见图2)，其中(XP,YP,ZP)为实验坐标系和(x,y,z)为晶体坐标系.图2(a)表示晶体坐标系与实验坐标系的关系，通过采用欧拉角(θ,φ,φ)和方向余弦的3次旋转操作确定；图2(b)表示晶坐标系，氧化锌结晶结构为六方晶系.激光从ZP方向照射.

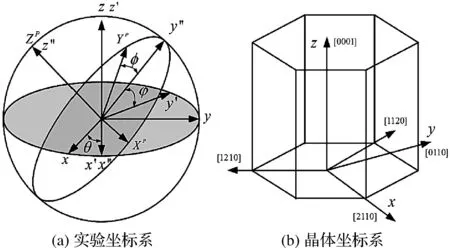
图2 拉曼光谱坐标系

1.3 应变产生的电压变化

因负荷应变会使原子间隔发生变化，从而导致电压也会发生变化.在此，可将微变形中多轴应变状态下的电压变化量V，根据公式(1)中的拉曼张量，表示为以下公式[8]:

(2)

式中：εij—结晶坐标系(x,y,z)中的应变分量；

Vij(i,j=x,y,z)—应变分量的电压变化率.

式(2)右边第1项表示对应A1振动模式、第2项表示对应E1振动模式、第3项表示对应E2振动模式的势能变化量.对应各振动模式的该电压变化，因与图1所表示的各振动模式的拉曼峰值移动量相对应，所以结晶坐标系(x,y,z)的应变负荷与各振动模式的拉曼位移的变化量可用以下公式表示[8].

对于A1模的拉曼频移应变关系式为：

(3)

对于E1和E2两种拉曼模的拉曼频移应变关系式为：

(4)

其中，E1/2表示E1和E2两种拉曼模.

2 拉曼频移应力关系式

根据广义Hooke定律[9]，横观各向同性材料的应力—应变关系为：

(5)

另外，式(5)中各刚性值[10](见表1).

通过式(3)、(4)和(5)可以得到拉曼频移与应力.

对于A1模的拉曼频移应力关系式为：

(6)

表1 氧化锌晶体的弹性常量

对于E1和E2两种拉曼模的拉曼频移应力关系式为：

(7)

其中，E1/2表示E1和E2两种拉曼模.

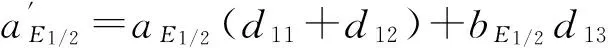
3 结 论

本研究从氧化锌的基本性质出发，建立氧化锌材料的横观各向同性力学模型，之后从微扰势出发并结合胡克定律，推导出氧化锌材料的拉曼频移—应力关系式，在确定ZnO拉曼频移—应力系数后，通过式(6)和式(7)和以及A1模(378 cm-1、579 cm-1)、E1模(407 cm-1、590 cm-1)和 E2模(99 cm-1、437 cm-1)拉曼频移量，共计6个独立方程式联立求解得到各应力分量.氧化锌的拉曼频移—应力定量关系的建立，为后续ZnO残余应力测量提供理论依据.

[1] 陈玉安，周上祺.残余应力X射线测定方法的研究现状[J].无损检测，2001，23(1):19-22.

[2] SHRESTHA S L, BREEB A J, TRIMBY P，et al. An automated Method of Quantifying Ferrite Microstructures Using Electron Backscatter Diffraction (EBSD) data [J].Ultramicroscopy, 2014,137(1):40-47.

[3] ABBAS E, MORTEZAS, MSDDOMRH E, et al. Evaluation of Microstructure and Texture across the Welded Interface of Super Duplex Stainless Steel and High Strength Low Alloy Steel, Surface & Coatings Technology[J].2015(264):150-162.

[4] 邓卫林,仇 巍,焦永哲，等，硅基底多层薄膜结构材料残余应力的微拉曼测试与分析[J].实验力学，2012,27(1):1-9.

[5] WAGNER JM, BECHSTEDT F. Properties of Strained Wurtzite GaN and AlN: Ab initio Studies [J]. Physical Review B, 2002,66(11):1-20.

[6] WAGNER JM, BECHSTEDT F. Phonon Deformation Potentials of GaN and AlN: An ab initio Calculation [J]. Applied Physics Letters, 2000,77(3):346-348.

[7] R. LOUDON. The Raman effect in crystals [J]. Advances in Physics, 2001,50(52):813-864.

[8] 刘 武.氧化锌残余应力拉曼光谱测量技术研究[D].天津：天津职业技术师范大学，2016.

[9] 俞文海，刘皖育.晶体物理学[M].合肥:中国科学技术出版社,2010.

[10] DECREMPS F, JULIO PP, SARRA A M, et al. High-pressure Raman Spectroscopy Study of Wurtzite ZnO[J]. Physical Review B,2002,65(9):92-101.

Quantitative Relationship Between Raman Frequency Shift and Stress of ZnO

LIU Wu1, ZHAO Hua-cheng2, XIANG chun1, LU Kong-bao1

(College of Mechanical and Automotive Engineering, Zhejiang University of Water Resources and Electric Power,Hangzhou 310018, China; 2.Engineering Experimental Training Center, Zhejiang University of Water Resources and Electric Power, Hangzhou 310018, China)

It is very important to grasp the stress states in the sub-area for the fabrication of MEMS devices. Raman stress measurement theory suitable for ZnO material was investigated, analytical mathematical expressions for the relationship between the Raman shift and the stress was deduced. This material belongs to 6mm point group with twoA1、E1andE2vibration mode Raman lines. The relationships between the change of Raman shift and stress component forA1、E1andE2models are theoretically derived based on perturbation potential and Hooke’s law. In these equations, 20 unknown parameters are included. The relationship between the Raman shift and the stress is put forward, which is helpful to provide a theoretical guidance in the ZnO residual stresses.

zinc oxide; Raman frequency shift; stress

2016-12-03

浙江省水利厅科技计划基金资助项目(RC1550)

刘 武(1989-)，男，湖北随州人，硕士，助理实验师，从事拉曼光谱应力测量方面的工作.

TE112

A

1008-536X(2017)04-0065-03