深度卷积神经网络的数据表示方法分析与实践

王佩琪 高 原 刘振宇 王海霞 汪东升

1(清华大学计算机科学与技术系 北京 100084)2(清华信息科学与技术国家实验室(筹) 北京 100084)

深度卷积神经网络的数据表示方法分析与实践

王佩琪1,2高 原1,2刘振宇2王海霞2汪东升2

1(清华大学计算机科学与技术系 北京 100084)2(清华信息科学与技术国家实验室(筹) 北京 100084)

(wpql4@mails.tsinghua.edu.cn)

深度卷积神经网络在多个领域展现了不凡的性能，并被广泛应用.随着网络深度的增加和网络结构不断复杂化，计算资源和存储资源的需求也在不断攀升.专用硬件可以很好地解决对计算和存储的双重需求，在低功耗同时满足较高的计算性能，从而应用在一些无法使用通用CPU和GPU的场景中.在专用硬件设计过程中仍存在着很多亟待解决的问题，例如选择何种数据表示方法、如何平衡数据表示精度与硬件实现代价等.为解决上述问题，针对定点数和浮点数建立误差分析模型，从理论角度分析如何选择表示精度及选择结果对网络准确率的影响，并通过实验探究不同数据表示方法对硬件实现代价的影响.通过理论分析和实验验证可知，在一般情况下，满足同等精度要求时浮点表示方法在硬件实现开销上占有一定优势.除此之外，还根据浮点表示特征对神经网络中卷积操作进行了硬件实现，与定点数相比在功耗和面积上分别降低92.9%和77.2%.

深度卷积神经网络；数据表示方式；浮点数据表示；定点数据表示；卷积操作优化

卷积神经网络(convolution neural network, CNN)因为其高准确率，广泛应用于语音分析、图像识别、自动驾驶等[1-3]多个热门研究领域.独特的权值共享网络结构使得CNN在处理二维数据方面取得了突破性进展.为进一步提高网络准确率，研究者们选择尽可能多地增加卷积神经网络层数，采用更为复杂的连接结构，旨在学习出更多高维度特征信息.例如，2014年ILSVRC竞赛(image net large scale vision recognition challenge)的冠军模型GoogLeNet[4]具有22层，采用了“Inception”连接结构，将多个不同大小的卷积核并行操作，所得结果通过直接连接作为下一层的输入数据.复杂结构的引入使得卷积神经网络计算过程越来越复杂.

结构复杂的深度卷积神经网络包含了更多权值，同时也产生了大量的计算需求.通常情况下，较为昂贵的高性能服务器可以用来满足计算和存储需求，但在一些特殊场景下，限于成本或是一些低功耗、空间限制等特殊需求，服务器很难满足要求.专用硬件可以在一定程度上很好地解决上述问题，但在设计过程中仍存在一些问题没有得到有效地解决，如数据表示方式和精度的选择等.在之前的研究中，一部分工作[5-7]采用定点表示方法计算CNN，利用定点计算硬件实现代价小、运算快等特点对CNN进行加速.另一部分[8-9]选择采用浮点表示方法来保证网络的准确率和性能.由此可见，选择何种数据表示方式不仅取决于网络对准确率的要求，而且会对硬件实现开销产生影响.例如，对同一数据，使用更多位数表示数据可以保证更高的准确率，但同时又会带来能耗和面积的增加.

我们通过研究发现，因为神经网络本身较强的鲁棒性，在一般情况下，浮点数与定点数相比具有一定优势：可以用更少的位数实现与定点数相同的精度.通过巧妙地硬件设计与实现，采用浮点数可以有效降低专用硬件实现开销.本文的贡献主要有3点：

1) 提出浮点数和定点数误差分析模型，并根据该模型在理论上分析数据表示方式对网络准确率的影响；

2) 根据浮点数和CNN自身特性，我们对卷积计算硬件实现进行设计，有效减少了计算过程的能量消耗，并进一步通过实践验证了在一般情况下，浮点表示具有一定优势；

3) 硬件仿真模拟显示，采用浮点数进行卷积操作时，在保持原有吞吐率前提下功耗和面积都得到了很大程度的降低.

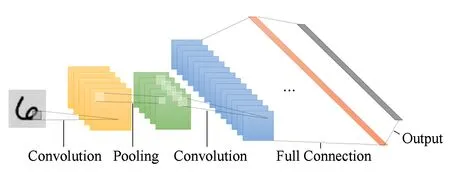
Fig. 1 A typical structure of convolution neural network图1 卷积神经网络结构示意图

1 卷积神经网络

为了更准确地分析出2种数据表示方式在卷积神经网络实现过程中产生的影响，我们先对CNN进行简单介绍.图1给出了典型的卷积神经网络层级结构.尽管不同CNN网络模型结构不尽相同，但基本上均包含3个基本结构：卷积层、下采样层(也称为抽样层)、全连接层(也称感知层).卷积层的主要功能是提取输入数据特征.卷积操作采用局部感受域和权值共享的方法，逐层提取更高维度的输入特征.在CNN中，输入数据中一小部分连续区域被称之为局部感受域，该区域是最底层计算结构单元，通过与对应权值(即数字滤波器)进行卷积操作得到相应特征.局部感受域结构对图像平移、比例缩放、倾斜或者其他形式的变形具有很强的鲁棒性.其中，权值在整张输入特征图计算上进行共享，从而降低了网络模型的复杂度，并且避免了传统识别算法中复杂的特征提取和数据重建过程.一般地，卷积层可计算为

(1)

其中，foutj表示该层第j张特征图输出结果，fini为第i张输入特征图值，filterij是计算所需的相应权值(滤波器数值)，biasj表示第j张输入特征图的对应偏置，函数δ(x)表示激活函数.

经过卷积操作后，输入数据的局部特征被提取出来并映射到一个平面，即为输出结果.此时激活函数对该结果进行特征映射，使得其具有位移不变性.激活函数用来模拟生物神经网络的激活现象，常用函数有sigmoid,tanh,ReLU(rectified linear unit), PReLU(parametric rectified linear unit)等.根据不同的应用场景和数据特征，CNN常常选择不同的激活函数.

每次特征提取之后，可以选择性地在卷积层后面设置下采样层.顾名思义，下采样层对卷积输出结果进行局部平均(mean-pooling)或最大值选取(max-pooling)，减小数据规模，同时使得网络对输入数据拥有较高的畸变容忍能力.

CNN网络在多层卷积和下采样叠加后，往往会紧跟着一个或多个全连接层.全连接层的结构与多层感知器几乎相同.该层的输出不再是二维结果，而是通过输入向量和权值向量相乘得到一维输出向量，并使用激活函数将结果进行特征映射，即：

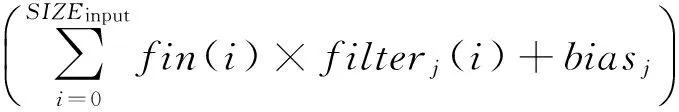
(2)

其中,fout(j)表示该全连接层输出向量中的第j个分量值.最后一层全连接输出结果往往被认定为整个网络的结果，即可以将最后一层视为分类层.

2 数据表示

在神经网络实现过程中，常用的2种数字表示方式是浮点和定点，选择哪种表示方式取决于应用需求.基于CPU和GPU计算时，往往会出于对表示范围和精确度的考虑选择浮点进行数据表示；而在专用芯片设计中，往往会选择定点来进行表示，因为与相同位数的浮点数计算相比，定点数的乘法、加法等基础计算在使用门电路实现时运算比较快，硬件代价小.但是无论哪种数据表示方式，显然所需表示位数越少，硬件实现开销越低.

图2给出了2种数据的表示格式.定点数用实数乘以2-i后的二进制结果近似表示.如图2(a)所示，一部分高位位数用来表示整数部分，其余低位表示分数部分，最高位表示符号.小数点的位置决定了整数和小数部分位数占比分配，同时这也就决定了数据表示范围和表示精度.浮点数通过科学计数法来表达实数，即通过一个基数(即进制)、一个指数和一个尾数来表达.在IEEE 754标准[10]中，浮点数的表示格式如图2(b)所示，通过尾数和可以调节的指数就可以表达给定数值.其中指数可正可负，在处理负指数时还需要加上一个偏差值保存在指数域中.我们可以笼统地认为，浮点数的表示范围主要由指数域位数决定，表示精度主要由尾数域位数决定.

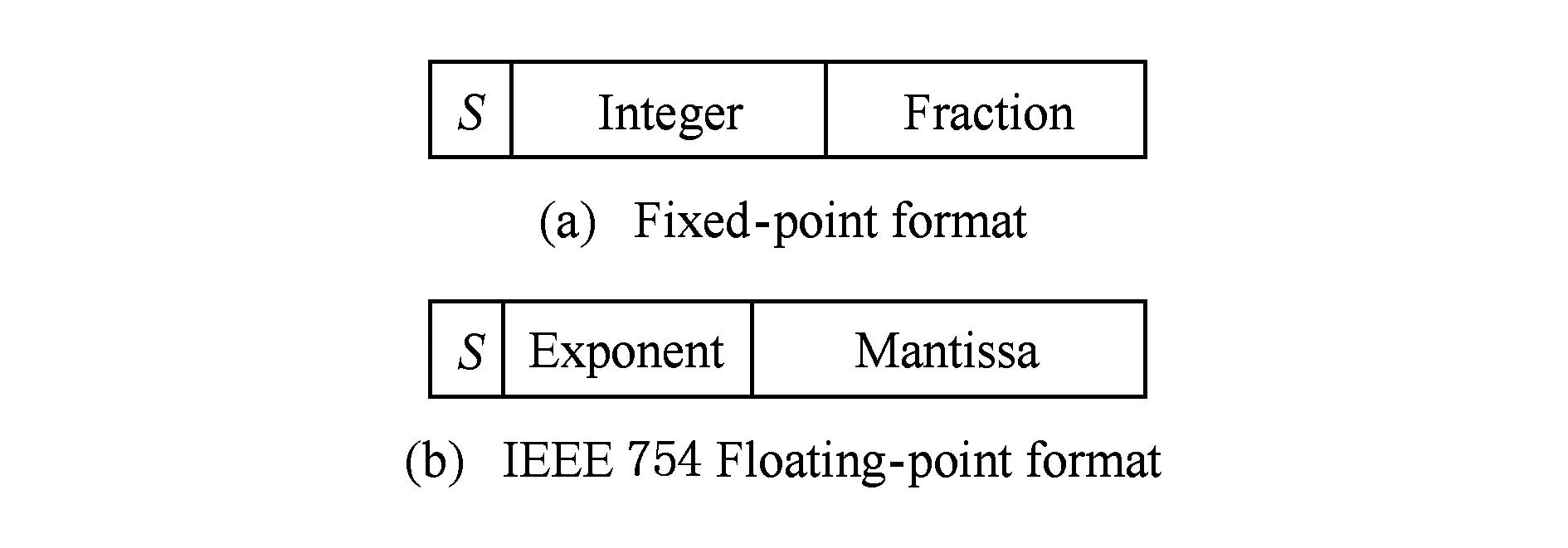
Fig. 2 Standard formats of fixed-point and floating-point representations图2 定点数和浮点数的标准格式

因为神经网络模型本身具有特殊性，在计算过程中既需要数据在很大的动态范围内进行变化，又需要在某些层内有很高的表示精度.定点表示方法实际上并不占优势，满足上述2个条件意味着整数部分和小数部分所需表示位数都很多.因此，在很多情况下，只能选择牺牲神经网络精确度来降低硬件开销.与之相比，浮点数因为其本身表示方法的特殊性，可以很好地满足神经网络对数据表示的要求.一方面，相同位数情况下，浮点因为采用科学计数法，所能表示的动态范围远大于定点；另一方面，标准IEEE浮点表示方法中要求所有数据表示格式为1.fraction× 2expont，并在实际二进制表示时省略表示前面整数部分1，因此也额外带来了一定程度上的位数优势.当然，浮点数的乘加运算十分复杂，硬件开销比定点数计算大，而且还会引入额外误差.接下来，我们将会针对该问题进行详细分析.

3 深度卷积网络误差模型

在本节的理论推导中，假设各种数据表示都会保证足够大的动态范围，从而避免上溢发生；假设通过优化非线性函数的分段，消除了拟合误差[11]，则舍入误差成为唯一误差源.

3.1 基于定点表示的卷积网络误差模型

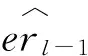
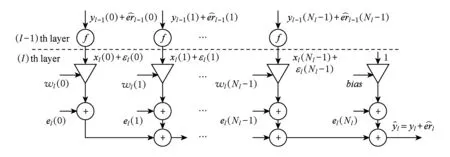
Fig. 3 Flow graph of error in fixed-point convolution图3 定点数据表示的卷积操作误差流图

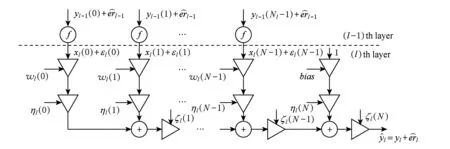
Fig. 4 Flow graph of error in floating-point convolution图4 浮点数据表示的卷积操作误差流图

由模型可知，来自上一层的输出信号连同噪声首先会经过一层非线性激活函数.在这里我们考虑常用函数sigmoid或者tanh，因此通过一阶泰勒级数展开有：

(3)

故得：

(4)

尽管不同非线性激活函数导数不同，从而对于误差传播产生不同影响，但是绝大多数导数在正负区间内都是单调的，所以：

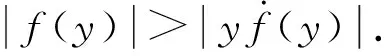
(5)

我们可以推导出激活函数的输入噪信比与输出噪信比大小关系：

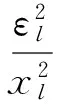
(6)

通过式(6)可知，非线性激活函数并不会使得输出噪信比恶化，所以在求取输出噪信比上限时可以忽略非线性激活函数影响.参考文献[12]和式(6)，第l层输出噪信比为

(7)

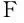
综上分析，对于一个共L层深度的卷积网络来说，输出噪信比上限为

(8)

3.2 基于浮点表示的卷积网络误差模型

图4给出了基于浮点表示的卷积操作误差流图.与定点不同，浮点乘法与加法操作均会引入乘性舍入误差.根据文献[12]，同理可推导出误差上限：

(9)

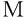
关于误差模型更多理论推导和分析过程可参见文献[13]，本文不再进行赘述.

3.3 数据表示精度对网络准确率的影响

为了探究不同数据表示方法和位数选择对神经网络准确率的影响，我们选择了3个不同规模卷积神经网络在深度学习框架Caffe上进行实现，如表1所示.

LeNet-5[14]是最早的卷积神经网络之一，推动了深度学习领域发展.该网络规模极小，应用在Minst数据集上对灰度手写数字进行识别.LeNet-5中采用的许多概念对后续研究起到了巨大影响力，如使用卷积操作提取空间特征、将数据映射到空间均值下采样等.CIFAR-10准确来讲并不是一个神经网络模型而是一个数据集，这里用于指代Caffe深度学习框架[15]中作用在CIFAR-10数据集上的神经网络模型.这里我们仅用数据集名称作为标识与其他网络模型进行区分.AlexNet[16]将LeNet-5核心思想扩展到了更大规模、能提取出更深维度数据特征的神经网络上，与之前神经网络相比规模上有了很大提升，属于大型神经网络中典型代表.在整个理论分析和实验过程中，我们只考虑前向判断(inference phrase)过程.因为在工业界实际应用中多采用线下训练的方式，用户端只需进行前向判断即可.

Table 1 Parameters of Popular Convolution Neural Networks表1 卷积神经网络模型参数

采用有限字长二进制进行实数表示时，位数越少，产生的误差就越大.与当前大多数研究采用的方法相似，我们在网络实现过程中采用32位浮点数进行训练，得出理想的精确结果；然后将这些参数舍入成不同配置，对测试结果准确度进行分析.图5给出了定点数和浮点数位数选择对3个神经网络准确度的影响情况，可以看到，当位数达到一个“上界”时，网络准确率几乎就不再变化;而随着网络规模增加，浮点与定点表示所需的最佳字长都会增加，这是由于各个卷积层的误差累计所造成.除此之外，定点表示相较于浮点所需字长增加趋势更加明显.以CIFAR-10为例，我们可以看到最终2种表示方法的错误率都保持在24.5%，浮点数尾数所需位从4位开始，错误率就开始逐渐降低，直到8 b时达到稳定；而定点数的小数位从4 b开始直至6 b错误率都很高，直到7 b时才有了下降趋势，并且最终需要8 b才达到稳定.所以我们认为在一般情况下，浮点表示比较定点更适合于大型网络.

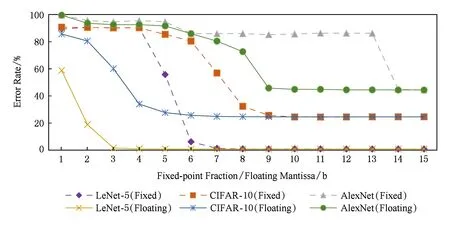
Fig. 5 Error rate vs word length图5 数据位数选择对网络准确率的影响

根据我们之前提出的定点和浮点卷积网络误差模型，我们分别对3个神经网络的最佳位数配置计算和统计了因有限字长实数表示而引入的噪信比误差，如表2所示.其中BF代表定点表示中小数域位数，BM代表浮点表示中尾数域位数.从表2中我们可以看出，无论定点数还是浮点数所引入的噪信比都很低，对网络最终准确率不会产生影响.

在硬件设计过程中，保证相同精度要求情况下，基于上述分析我们可以用少于定点位数的浮点数来对神经网络数据进行表示.随着网络规模增大，表示整个网络所有数据的动态范围也随之增加，因此浮点数的优势会更加明显.当前一些相关研究[17-18]会将网络进行一些量化处理，采用位数极少的定点数来进行计算.但在实际数据处理过程中，往往需要对量化后的数据进行展开从而带来一些额外代价；除此之外，这些研究中提到的优化方法同样也适用于浮点数，可以进一步优化表示所需位数，我们正在进行相关方面的研究.

综上所述，一般情况下，浮点数可以用少于定点所需位数来保证网络所要求的精度.考虑到硬件实现代价，虽然浮点数因为本身计算复杂性，同样位数条件下所需功耗和面积要大于定点数，但因浮点数本身特性可以在很大程度上减少自身表示位数，这样在硬件实现过程中极有可能带来能耗和面积上的降低.接下来，我们将通过实验对上述结论进行验证.

4 实验及结果分析

在实验部分，我们采用Verilog-HDL对传统卷积方法和数据为中心的卷积方法进行硬件层级描述，通过Synopsys Design Compiler等软件进行模拟、仿真、综合等工作.实验中使用TSMC 65 nm GP标准库，同时使用Artisan single-ported register file memory compiler对片上缓存进行模拟仿真.考虑到需要满足多个神经网络的精度需求，我们选择AlexNet网络的配置位数(定点数BI=11,BF=10；浮点数BE=5,BM=10)进行实验测试.

4.1 基本操作单元的实现

由式(1)(2)我们可以看出，乘法和加法是卷积神经网络中基本操作，因此我们选择两输入加法单元和两数乘法单元来进行硬件实现的比较和分析.表3给出了2种基本操作单元在不同数据表示方式下所需功耗和面积.从表3中我们可以看出，在两输入乘法单元的实现中，浮点数的优势比较明显，在面积与功耗上分别降低了55%和73.6%.因为标准浮点数采用科学计数法的方法表示，指数域只需进行加法操作即可;而浮点数加法计算需要进行对阶、移位、归一化等一系列额外操作，所以导致了两输入加法的功耗和面积都要大于定点计算.

在神经网络中，往往会对多个乘积结果进行累加.当前较为普遍的实现是采用加法树，可以保证计算精度.为了解决加法操作代价过大的问题，并且考虑到浮点表示特点，我们对加法硬件实现方法进行了改进.我们的计算方法是将多个浮点操作数的指数部分进行对齐，然后小数部分直接相加.因为卷积神经网络中归一化操作会使各个浮点结果之间相差不大，所以精度上的损失几乎可以忽略不计.表4中给出了16位浮点数采用传统加法树和直接相加2种方法时功耗和面积实现开销.从表4中我们可以看出，采用直接相加的方法可以在一定程度上降低硬件开销，4输入和8输入加法器分别带来了70.4%和74.4%在功耗方面的降低.

Table 3 Hardware Overhead with Fixed-point and Floating-point Arithmetic on AlexNet表3 AlexNet中定点表示与浮点表示的硬件实现开销

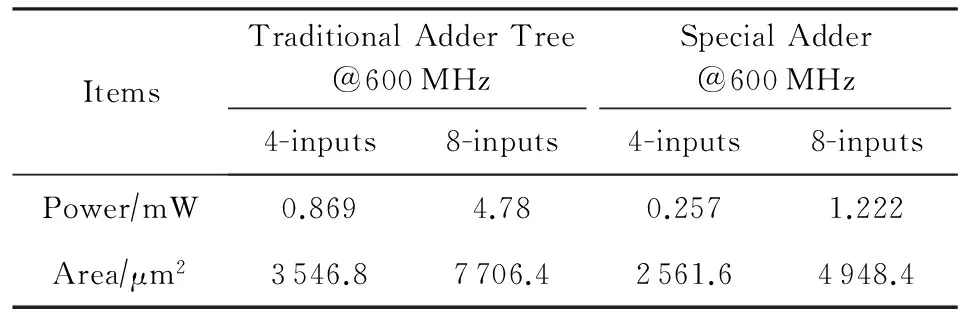
Table 4 Hardware Overhead of Different Adders表4 不同加法器的硬件实现开销

4.2 卷积操作的硬件实现

因为卷积在整个深度卷积神经网络的计算过程中占据了绝大部分，所以我们选择对卷积操作进行硬件模拟仿真，验证使用浮点数据表示方式对深度神经网络硬件实现过程所带来的优势.实际上，我们实现了一个可以处理整个卷积神经网络的硬件结构，片上系统中存储设计和控制逻辑采用与之前研究工作[5]相似的设计.但是为了更准确地对卷积操作部分进行分析，排除片上其他计算单元和元器件对性能产生影响，我们将卷积操作的基本计算基元阵列(processing engines, PEs)实验结果单独提出进行分析比较.

在进行卷积操作计算时，为了充分利用浮点数带来的硬件实现优势，我们将传统卷积操作进行分解计算.一个K×K大小滤波器的卷积操作可以被分解为K个乘加分量，每个分量是在该K×K大小感受域中同一行数据计算结果加和.具体数据流和计算方法可参考文献[19].图6给出了以3×3大小滤波器为例，基本计算单元PE阵列结构示意图.PE基元我们采用两输入乘法单元，而加法器则采用本文提出的加法器设计.为了让PE阵列既可以计算卷积层，又可以计算全连接层，我们加入了多个二路选择器和D触发器.在卷积层计算中，4输入加法器最后一个分量选择上一行的计算结果，即D触发器的输出结果(如图6中实线所示)；在全连接层计算中则选择本行的计算结果进行累加(如图6中虚线所示).

Fig. 6 Structures of PE arrays图6 PE阵列硬件实现结构示意图

为了平衡卷积层和全连接层计算，并满足深度卷积网络的计算需求，实验设置PE阵列大小为16×16；输入数据大小设置为常用标准图片大小，即256×256.在实验过程中，我们只考虑前向过程，因为在工业界实际应用中多采用线下训练的方式，用户端只需进行前向判断即可.表5给出了分别采用2种不同卷积方式下的硬件功耗和面积.从表5中我们可以看到，利用浮点数表示特点进行数据为中心的卷积计算方法，同时采用定制浮点加法器部件，浮点数表示与定点数相比，可以节省了92.9%的能量消耗，且面积也减少了77.2%.在接下来的工作中，我们会对片缓存结构进行优化，使其适应这种数据为中心的卷积操作，进一步提升系统性能.除此之外，未来我们也会对全连接层的计算进行相关优化和研究.

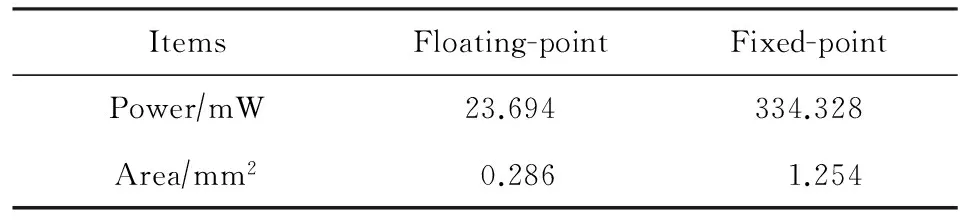
Table 5 Overhead of PE Arrays Using Different Numeric Representations @600 MHz

5 相关工作

当前有很多研究机构和人员对神经网络硬件加速和优化方面进行探索，并得出了很多有意义的成果.与软件算法层级加速和优化相比，硬件系统优化更容易满足深层和复杂的网络结构.

在专用硬件系统实现过程中，选择合适的数据表示方法是一个重要环节.定点数和浮点数是2种较为常见的表示方法，不同应用会根据自身需求选择不同精度表示.例如，文献[6-7,20]采用16 b定点数，文献[21-22]采用48 b定点数，文献[23]采用32位单精度浮点数进行数据表示.研究者们根据经验或实践来进行数据表示方法和表示精度的选择，往往没有较为完善的理论模型对决策结果进行支持.在传统多层感知器网络中，Holi等人[23]提出了一种误差分析理论模型，该模型中在网络前向和后向2个阶段中使用定点数据表示，并只针对单一错误源.因此，其他错误源所引入的误差在该模型中被忽略.在最近研究中，Courbariaux等人[24]提出在神经网络训练过程中，动态定点表示方法可以满足Maxout网络对精度的需求.该文中提出了几种在Maxout网络计算中可以达到同等精度的表示方法：16 b浮点、20 b定点以及10～12 b混合动态定点表示方法，并最终采用了位数最少的动态定点表示法.实际上，这种表示方法会在硬件实现过程中隐式地引入额外硬件开销.Gupta等人[25]关注于神经网络训练中有限定点数字长会对网络本身准确度和性能产生怎样的影响，并且该文提出了一种数据舍入方案，在训练阶段(learning phase)占据了重要地位.但是这种基于批次处理的数据处理方法无法很好地应用在测试阶段(testing phase).与之前研究工作相比较，本文提出的误差分析模型则可以很好地应用在测试阶段，并且对于深度卷积神经网络中定点和浮点2种表示方法都可以进行误差分析.

专用硬件设计上，近几年也出现了很多十分有研究价值和借鉴意义的成果，如文献[9]中提到对CNN性能的分析建模方法，通过模型分析出网络硬件实现过程中的性能瓶颈和可优化部件；又如中科院“寒武纪”项目中的系列研究工作，其中既有单个节点加速结构[5]，又有可以将所有权值都存储在片上多节点加速系统[6].因为一些新兴技术涌现与发展，神经网络加速硬件设计与实现方法又涌现了新的可能性.文献[26-27]中采用了新型忆阻器作为存储和计算元件，很大程度地提升了性能.此外，3D堆叠基础和内存计算等技术也用于硬件设计之中.

6 结 论

本文研究了在神经网络计算过程中，2种最为常见的表示方法(浮点数和定点数)对神经网络准确度以及硬件实现代价的影响.本文基于这2种表示方法分别建立了误差分析模型，并根据模型从理论角度分析了如何选择表示位数以满足网络对精度的需求.我们发现在一般情况下，表示同等精度时浮点数所需位数少于定点数.因此，结合IEEE 754标准浮点表示特征，我们通过实验验证了使用浮点数可以在神经网络硬件实现中有效地降低功耗和面积，分别减少了92.9%和77.2%.在最近的研究工作中，一些研究工作通过对网络模型算法本身优化[17]，如经过微调或重训练等方法，用很少的定点位数即可满足网络精度需求.实际上浮点数经过上述优化，也可以进一步减少表示位数.在未来研究工作中，我们将采取一系列算法级优化处理，进一步减少数据表示位数需求，从而在更大程度上降低神经网络硬件实现代价.

[1]Girshick R, Donahue J, Darrell T, et al. Rich feature hierarchies for accurate object detection and semantic segmentation[C] //Proc of the IEEE Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2014: 580-587

[2]Garcia C, Delakis M. Convolutional face finder: A neural architecture for fast and robust face detection[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 2004, 26(11): 1408-1423

[3]Zou A M, Kumar K D, Hou Z G, et al. Finite-time attitude tracking control for spacecraft using terminal sliding mode and Chebyshev neural network[J]. IEEE Trans on Systems, Man, and Cybernetics, Part B (Cybernetics), 2011, 41(4): 950-963

[4]Szegedy C, Liu W, Jia Y, et al. Going deeper with convolutions[C] //Proc of the IEEE Conf on Computer Vision and Pattern Recognition. Piscataway, NJ: IEEE, 2015: 1-9

[5]Chen Tianshi, Du Zidong, Sun Ninghui, et al. Diannao: A small-footprint high-throughput accelerator for ubiquitous machine-learning[J]. ACM Sigplan Notices, 2014, 49(4): 269-284

[6]Chen Yunji, Luo Tao, Liu Shijin, et al. Dadiannao: A machine-learning supercomputer[C] //Proc of the 47th Annual IEEE/ACM Int Symp on Microarchitecture. Los Alamitos, CA: IEEE Computer Society, 2014: 609-622

[7]Du Zidong, Fasthuber R, Chen Tianshi, et al. ShiDianNao: Shifting vision processing closer to the sensor[J]. ACM SIGARCH Computer Architecture News, 2015, 43(3): 92-104

[8]Qiu Jiantao, Wang Jie, Yao Song, et al. Going deeper with embedded FPGA platform for convolutional neural network[C] //Proc of the 2016 Special Interest Group on Design Automation of the Association for Computing Machinery (ACM/SIGDA) Int Symp on Field-Programmable Gate Arrays. New York: ACM, 2016: 26-35

[9]Zhang Chen, Li Peng, Sun Guangyu, et al. Optimizing FPGA-based accelerator design for deep convolutional neural networks[C] //Proc of the 2015 Special Interest Group on Design Automation of the Association for Computing Machinery (ACM/SIGDA) Int Symp on Field-Programmable Gate Arrays. New York: ACM, 2015: 161-170

[10]Overton M L. Numerical Computing with IEEE Floating Point Arithmetic[M]. Philadelphia, PA: Society for Industrial and Applied Mathematics, 2001

[11]Vassiliadis S, Zhang M, Delgado-Frias J G. Elementary function generators for neural-network emulators[J]. IEEE Trans on Neural Networks, 2000, 11(6): 1438-1449

[12]Oppenheim A V, Weinstein C J. Effects of finite register length in digital filtering and the fast Fourier transform[J]. Proceedings of the IEEE, 1972, 60(8): 957-976

[13]Gao Yuan, Liu Zhenyu, Wang Dongsheng. Error models of finite word length arithmetic in CNN accelerator design[C] //Proc of 2016 Visual Communications and Image Processing (VCIP). Piscataway, NJ: IEEE, 2016: 1-4

[14]LeCun Y, Bottou L, Bengio Y, et al. Gradient-based learning applied to document recognition[J]. Proceedings of the IEEE, 1998, 86(11): 2278-2324

[15]Jia Yangqing, Shelhamer E, Donahue J, et al. Caffe: Convolutional architecture for fast feature embedding[C] //Proc of the 22nd ACM Int Conf on Multimedia. New York: ACM, 2014: 675-678

[16]Krizhevsky A, Sutskever I, Hinton G E. Imagenet classification with deep convolutional neural networks[C] //Proc of Advances in Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2012: 1097-1105

[17]Han Song, Liu Xingyu, Mao Huizi, et al. EIE: Efficient inference engine on compressed deep neural network[C] //Proc of the 43rd Int Symp on Computer Architecture. Piscataway, NJ: IEEE, 2016: 243-254

[18]Hubara I, Courbariaux M, Soudry D, et al. Binarized neural networks[C] //Proc of Advances in Neural Information Processing Systems. Red Hook, NY: Curran Associates Inc, 2016: 4107-4115

[19]Wang Peiqi, Liu Zhenyu. Data-centric computation mode for convolution in deep neural networks[C] //Proc of 2017 Int Joint Conf on Neural Networks (IJCNN). Piscataway, NJ: IEEE, 2017: 133-139

[20]Sankaradas M, Jakkula V, Cadambi S, et al. A massively parallel coprocessor for convolutional neural networks[C] //Proc of the 20th IEEE Int Conf on Application-Specific Systems, Architectures and Processors (ASAP 2009). Piscataway, NJ: IEEE, 2009: 53-60

[21]Chakradhar S, Sankaradas M, Jakkula V, et al. A dynamically configurable coprocessor for convolutional neural networks[J]. ACM SIGARCH Computer Architecture News, 2010, 38(3): 247-257

[22]Farabet C, Poulet C, Han J Y, et al. CNP: An FPGA-based processor for convolutional networks[C] //Proc of Int Conf on Field Programmable Logic and Applications (FPL 2009). Piscataway, NJ: IEEE, 2009: 32-37

[23]Holi J L, Hwang J N. Finite precision error analysis of neural network hardware implementations[J]. IEEE Trans on Computers, 1993, 42(3): 281-290

[24]Courbariaux M, Bengio Y, David J. Low precision arithmetic for deep learning[J/OL]. arXiv:1412.7024, 2014

[25]Gupta S, Agrawal A, Gopalakrishnan K, et al. Deep learning with limited numerical precision[C] //Proc of the 32nd Int Conf on Machine Learning(ICML 2015). Madison, Wisconsin: Omnipress, 2015: 1737-1746

[26]Chi Ping, Li Shuangchen, Xu Cong, et al. PRIME: A novel processing-in-memory architecture for neural network computation in ReRAM-based main memory[C] //Proc of the 43rd Int Symp on Computer Architecture. Piscataway, NJ: IEEE, 2016: 27-39

[27]Shafiee A, Nag A, Muralimanohar N, et al. ISAAC: A convolutional neural network accelerator with in-situ analog arithmetic in crossbars[C] //Proc of the 43rd Int Symp on Computer Architecture. Piscataway, NJ: IEEE, 2016: 14-26

Wang Peiqi, born in 1994. PhD candidate. Her main research interests include computer architecture, deep neural network accelerator design and optimization.

Gao Yuan, born in 1991. PhD candidate. His main research interests include error analysis of digital system calculation and convolution neural network accelerator design.

Liu Zhenyu, born in 1973. PhD, associate professor. His main research interests include video coding algorithm, large scale integrated circuit design, image signal processing and multi-core processor simulation system.

Wang Haixia, born in 1977. PhD, associate professor. Her main research interests include computer architecture, network on chip, and memory hierarchy.

Wang Dongsheng, born in 1966. PhD, professor, PhD supervisor. His main research interests include computer architecture, distributed system, and accelerator design.

A Comparison Among Different Numeric Representations in Deep Convolution Neural Networks

Wang Peiqi1,2, Gao Yuan1,2, Liu Zhenyu2, Wang Haixia2, and Wang Dongsheng2

1(DepartmentofComputerScienceandTechnology,TsinghuaUniversity,Beijing100084)2(TsinghuaNationalLaboratoryforInformationScienceandTechnology,Beijing100084)

Deep convolution neural networks have been widely used in industries as well as academic area because of their triumphant performance. There are tendencies toward deeper and more complex network structures, which leads to demand of substantial computation and memory resources. Customized hardware is an appropriate and feasible option, which is beneficial to maintain high performance in lower energy consumption. Furthermore, customized hardware can also be adopted in some special situations where CPU and GPU cannot be placed. During the hardware-designing processes, we need to address some problems like how to choose different types of numeric representation as well as precision. In this article, we focus on two typical numeric representations, fixed-point and floating-point, and propose corresponding error models. Using these models, we theoretically analyze the influence of different types of data representation on the hardware overhead of neural networks. It is remarkable that floating-point has clear advantages over fixed-point under ordinary circumstances. In general, we verify through experiments that floating-point numbers, which are limited to certain precision, preponderate in both hardware area and power consumption. What’s more, according to the features of floating-point representation, our customized hardware implementation of convolution computation declines the power and area with 14.1× and 4.38× respectively.

deep convolution neural network; numeric representation; floating-point computation; fixed-point computation; convolution optimization

2017-02-27；

2017-04-13

国家自然科学基金项目(61373025)；国家重点研发计划项目(2016YFB1000303) This work was supported by the National Natural Science Foundation of China (61373025) and the National Key Research and Development Program of China (2016YFB1000303).

汪东升(wds@tsinghua.edu.cn)

TP183