基于概率分布的多峰演化算法
2017-06-23陈伟能
陈伟能 杨 强,2
1(华南理工大学计算机科学与工程学院 广州 510006)2(中山大学数据科学与计算机学院 广州 51006)
基于概率分布的多峰演化算法
陈伟能1杨 强1,2
1(华南理工大学计算机科学与工程学院 广州 510006)2(中山大学数据科学与计算机学院 广州 51006)
(eschenwn@scut.edu.cn)
2(SchoolofDataandComputerScience,SunYat-senUniversity,Guangzhou510006)
演化算法通过模拟自然界生物迭代演化的智能现象来求解优化问题,因其不依赖于待解问题具体数学模型特性的优势,已成为求解复杂优化问题的重要方法.分布估计算法是一类新兴的演化算法,它通过估计种群中优势个体的分布状况建立概率模型并采样得到子代,具有良好的搜索多样性,且能通用于连续和离散空间的优化问题.为进一步推动基于概率分布思想的演化算法发展,概述了多峰优化演化算法的研究现状,并总结出2个基于概率分布的演化算法框架:面向多解优化的概率分布演化算法框架和基于概率分布的集合型离散演化算法框架.前者针对现有的演化算法在求解多峰多解的优化难题时缺乏足够的搜索多样性的缺点,将广义上基于概率分布的演化策略与小生境技术相结合,突破多解优化的搜索多样性瓶颈;后者围绕粒子群优化等部分演化算法在传统上局限于连续实数向量空间的不足,引入概率分布估计的思想,在离散的集合空间重定义了算法的演化操作,从而提高了算法的可用性.
概率分布;演化算法;进化计算;多峰优化;计算智能
多峰优化问题(multimodal optimization problems)是指问题的解空间含有多个局部最优或全局最优解的一类优化问题.这类问题广泛存在于人们的日常生活和工业生产之中,例如旅行商问题(traveling salesman problem, TSP)、多重背包问题(multiple knapsack problem, MKP)等经典的组合优化问题[1],聚类、特征选择和分类等机器学习问题[2],功率电路设计[3]、网络设计等工业生产问题[4-5],车辆路由[6]、项目调度和金融管理优化等运筹调度问题[7-8],都属于多峰优化问题.随着科技的发展以及大数据时代的到来,这些优化问题日益复杂,如何有效地求解多峰优化问题已经成为工业生产和日常生活的迫切需求,也成为了计算机、运筹和控制等多个领域的研究热点.
由于这些实际优化问题往往不具备精确的数学解析模型,或其数学模型不具有连续、可导等数学特性,传统的数学优化方法难以求解.演化计算方法是通过模拟自然界生物迭代演化的智能现象来求解复杂优化问题的一类计算智能方法,具有不依赖于待解问题的精确数学模型和数学特性、全局寻优、在可接受的时间内能获得近似最优解等优势,已逐渐成为了求解复杂优化问题的重要方法[9-11].2015年《Nature》刊登的机器学习专刊也对演化算法的发展进行了专题报道[12].传统上,演化算法(evolutionary algorithm, EA)主要包括遗传算法(genetic algorithm, GA)[13]、遗传编程(genetic programming, GP)[14]、进化策略(evolutionary strategy, ES)[15]和进化编程(evolutionary programming, EP)[16]等模拟生物进化过程的算法.近15年来,演化算法的研究受到了广泛关注,其范畴也得到了进一步的拓展,如差分进化算法(differential evolution, DE)[17]和分布估计算法(estimation of distribution algorithm, EDA)[18]等基于改进的进化和变异方式的演化算法相继被提出;如粒子群优化(particle swarm optimization, PSO)[19]和蚁群优化(ant colony optimization, ACO)[20]等群体智能算法也作为演化算法的分支快速发展.
然而,复杂多峰问题的解空间中往往存在着非常多的局部最优解,部分局部最优解的峰区所涵盖的范围比较宽阔.随着问题维度的增加,多峰优化问题的局部最优解个数将快速增长,这对演化算法的搜索多样性提出了重大挑战.另外,部分多峰优化问题还可能存在多个峰值近似、均可接受的(近似)全局最优解,需要演化算法能同时发现尽可能多的这些可接受的全局最优解,以提供更准确的决策支持.这类多峰问题称为多峰优化的多解问题,其对演化算法的多样性提出了更高的要求.为有效求解多峰优化问题,如何在保持算法高效率以用较少的适应值评价次数来迭代演化的同时,提高算法的搜索多样性以避免算法落入局部最优,俨然是演化算法的关键,这也一直是演化算法研究的重点和热点.
为了有效解决多峰优化问题,学者们从不同角度、基于不同的演化算法,提出了各种各样的多峰演化算法,提高了演化算法求解多峰优化问题的效率和精度.特别地,如粒子群优化、差分进化等基于解之间的差值运算作为交叉或变异算子的演化算法,凭借其简单且有效的优势,吸引了广大学者的关注[17,21-23].然而,随着问题维度的扩大,峰值个数的增加,或者是在多样性要求更高的多峰优化多解问题上,基于差值运算作为进化算子的演化算法仍存在着容易落入局部最优、早熟收敛的瓶颈[19,24].同时,这类算法传统上一般定义于连续实数向量空间,难以直接应用于离散空间的组合优化问题[1].
近年来,一类新型的演化算法——分布估计算法(EDA)逐渐受到了关注[18].与传统的交叉、变异或者基于差值运算的进化操作不同,分布估计算法根据当前种群中的个体信息,评估种群演化的概率分布信息,并依据该概率分布采样产生子代个体.该算法评估种群演化的分布信息,能更宏观地把握整个空间的搜索情况,因此在算法的搜索多样性维护上具有很大优势.同时,概率分布估计策略能通用于连续型和离散型的决策变量,不受解空间连续、离散特性的限制.若能进一步突破这类算法的搜索效率瓶颈,将能为复杂的多峰优化问题提供高搜索多样性的有效解决途径.
狭义上,基于概率分布的演化算法一般指分布估计算法.广义上,概率分布的思想实际上也在其他多种演化算法中体现.例如蚁群优化算法(ACO)的基本思想是通过信息素记录种群搜索的历史信息,并基于信息素指导依概率为子代个体构建解,因此信息素的分布可以理解为一种特殊的概率分布[20].为了进一步探索基于概率分布的演化算法在复杂多峰优化问题上的应用,本文将阐述2类广义上基于概率分布的演化算法框架:面向多解优化的概率分布演化算法框架和基于概率分布的集合型离散演化算法框架.其中,前者围绕多峰问题多解优化等搜索多样性要求高的复杂多峰优化问题,通过将概率分布演化算法和小生境(Niching)[25]技术相结合,充分发挥概率分布演化算法具备良好搜索多样性的优势,克服演化算法在多解优化中容易早熟收敛的缺陷.基于这一框架,本文将介绍2类新型多解优化算法:多解优化的分布估计算法(multimodal EDA, MEDA)[26]和自适应的多解优化蚁群算法(adaptive multimodal ACO, AM-ACO)[27].另一方面,基于概率分布的集合型离散演化算法框架,能将传统定义于连续实数向量空间的粒子群优化等算法在集合空间中重定义,从而能够突破算法的解空间受限瓶颈,将算法拓展成通用于连续和离散空间的通解算法.
1 面向多峰优化的演化算法
1.1 多峰问题的单解演化算法
演化算法的思想是通过种群的迭代演化来不断逼近问题的最优解,其框架如算法1所示.
算法1. 演化算法基本框架.
输入: 种群大小NP、最大迭代次数GEN;
输出: 全局最优解.
① 初始化种群并评估每个个体的适应值;
②generation=0;
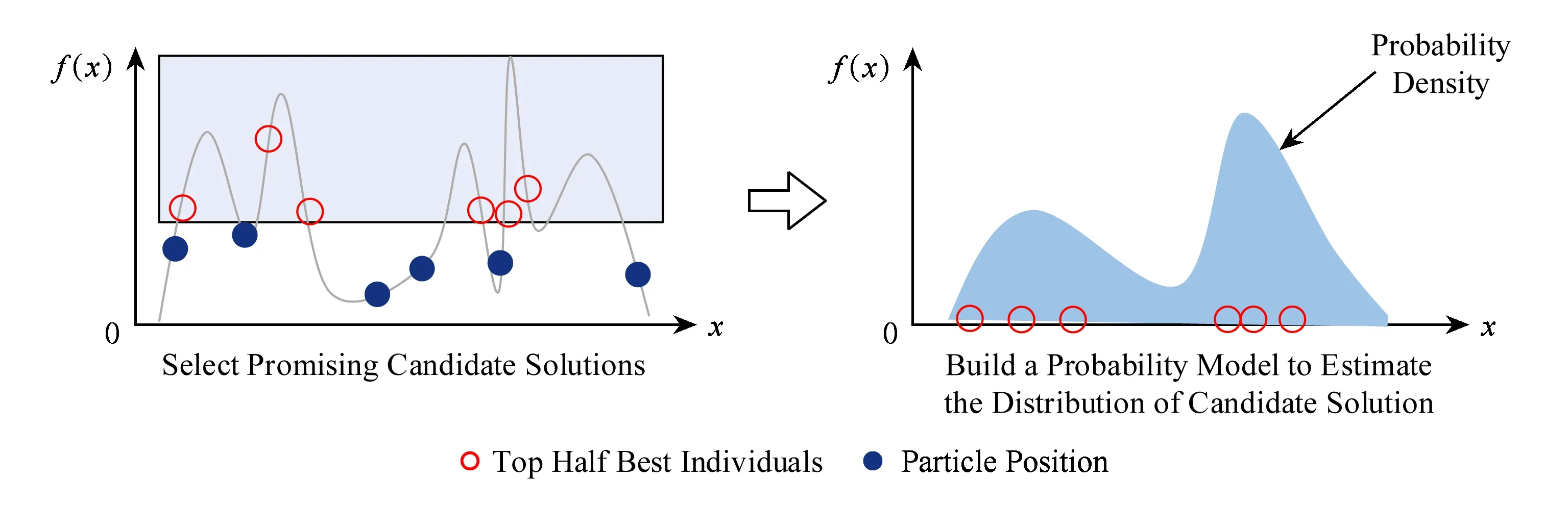
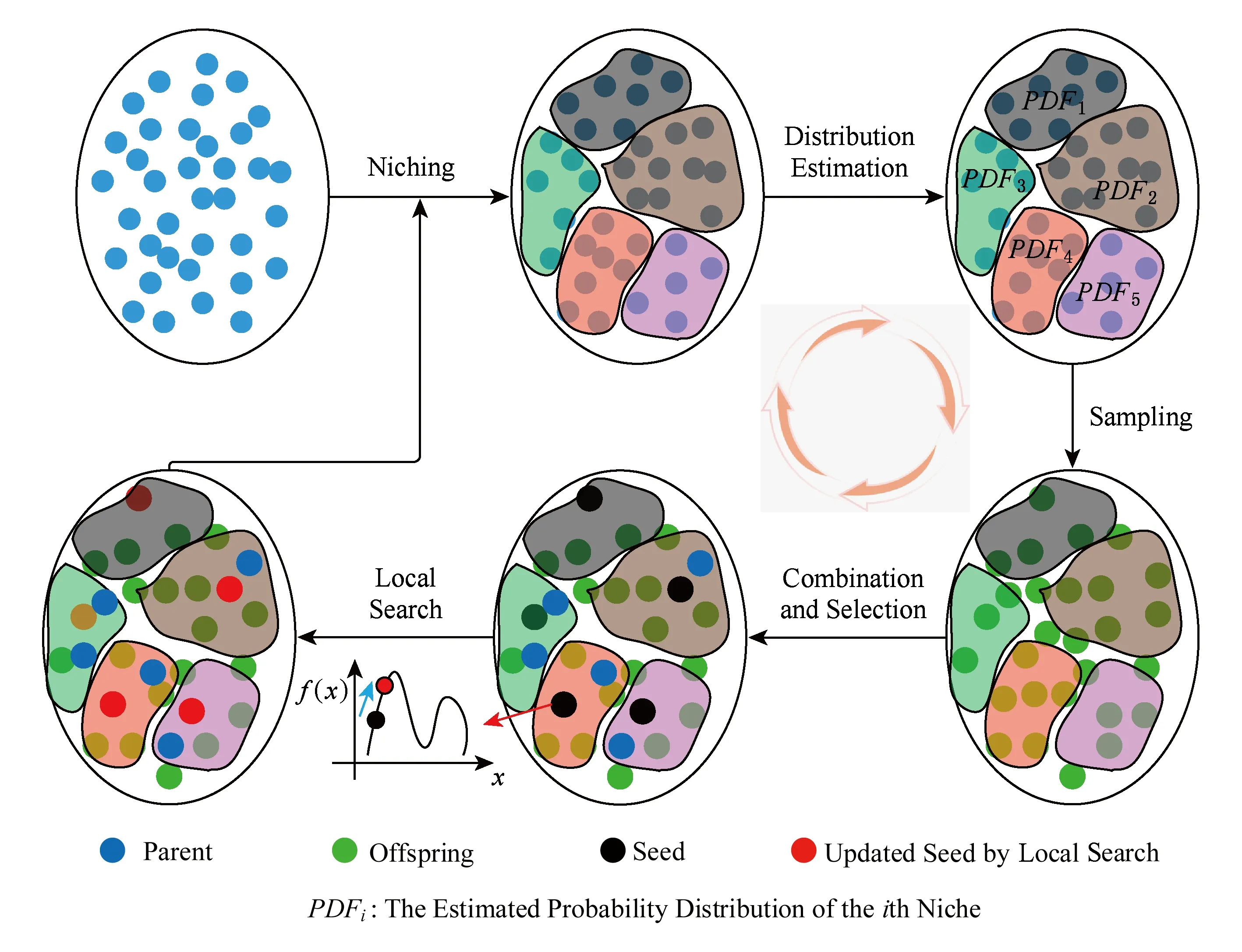
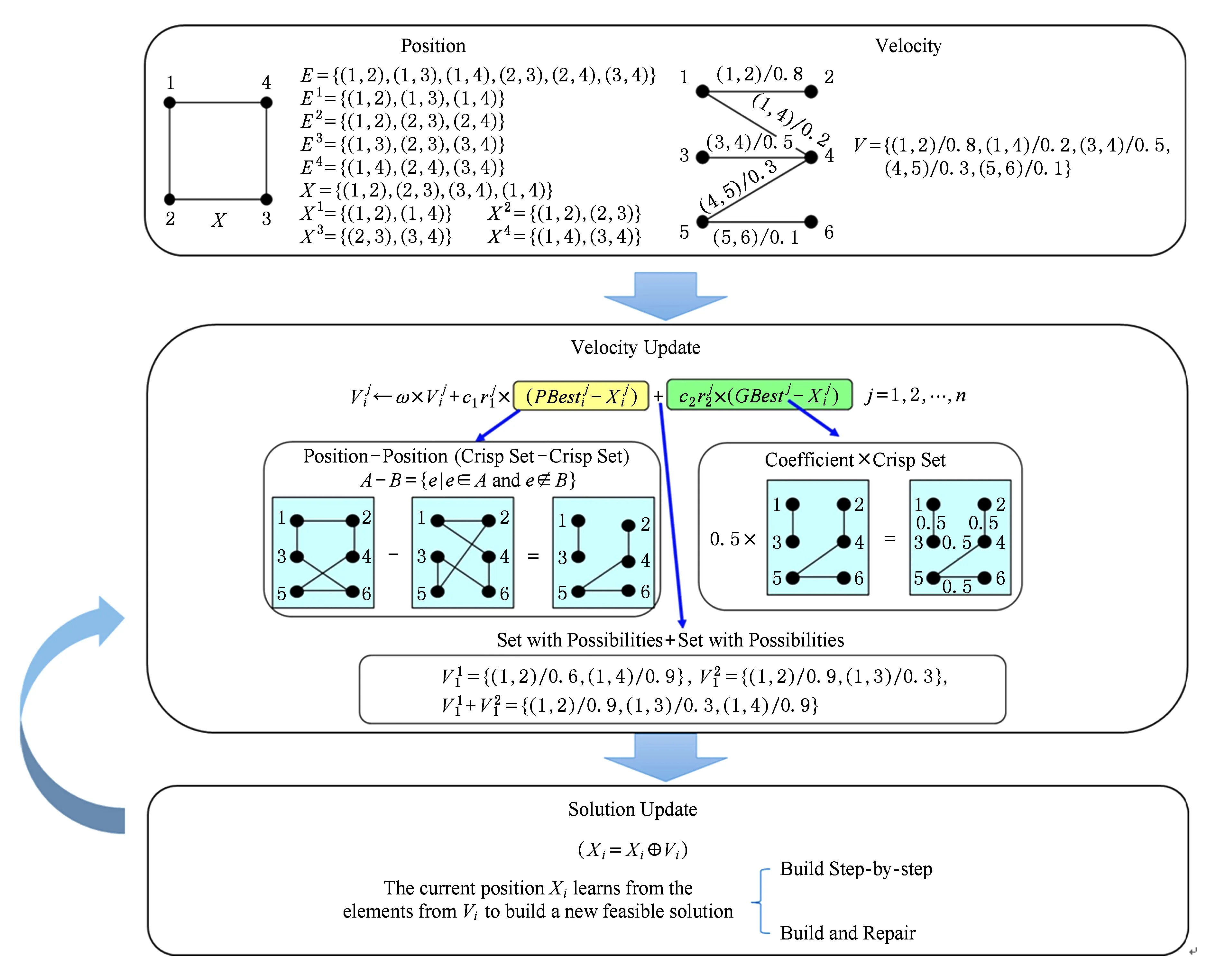
③ While (generation ④ 根据父代个体通过操作算子等操作得到子代个体; ⑤ 评估子代个体适应值; ⑥ 用子代个体淘汰差的父代个体并更新全局最优解gbest; ⑦generation++; ⑧ End While 不同的演化算法采用了不同的演化机制和演化算子.例如,GA通过模拟生物进化过程中染色体的交叉和变异操作来完成种群的演化;PSO通过个体向自我认知(即每个个体曾经搜索到达的最优位置pbest)和社会影响(即种群曾到达的最优位置gbest)学习的演化操作来迭代进化,其迭代公式为 vi=wvi+r1c1(pbesti-xi)+r2c2(gbest-xi), (1) xi=xi+vi, (2) 其中,实数向量xi,vi分别表示第i个粒子的位置和速度;pbesti是第i个粒子的历史最优解,gbest是整个种群所找到的历史最优解;w是惯性权重,r1和r2是在[0,1]内的随机数,c1和c2是加速因子. 传统上,多峰优化问题一般是指单解问题.尽管这类问题的目的在于只寻找优化问题解空间中的一个全局最优解,但由于问题的局部最优解众多,算法很容易落入局部最优,出现早熟收敛现象.为克服以上弊端,演化算法必须维持高搜索多样性,以协助种群逃离局部最优区域,同时又要节省适应值评价的使用次数,以提高算法搜索效率.为使演化算法既高效又具备足够的搜索多样性,学者们主要从3个角度开展研究并提出了众多演化算法的改进版本: 1) 演化算法的参数调节.演化算法的性能往往与算法的控制参数息息相关.例如,GA的性能受到了交叉和变异概率的影响,PSO的性能则受到了惯性权重w和加速因子c1,c2的影响.对不同类型的优化问题,在不同的演化阶段,这些控制参数的选择也各不相同.因此,如何动态自适应地为算法选择合适的控制参数,成为了研究焦点.目前,主要的参数自适应方法包括2类:①基于进化状态感知的自适应控制参数方法[21,28],即通过分析种群的适应值和分布特性,感知算法在进化过程中所处的进化状态,并最终根据算法所处的进化状态特征设定不同的参数调整策略;②参数自我调节(self-adaptive)策略[29-30],即根据种群适应值的变动情况,评价参数对算法性能的贡献程度,并动态自适应地调整某组参数被选择的概率,从而筛选出更有效的参数设置. 2) 演化算法的操作算子.尽管自适应调整控制参数能提高算法的搜索效率,但演化算子对算法的性能起到了更决定性的影响.图1描述了基于式(1)和式(2)的原始PSO算法的搜索特征. Fig. 1 The search behavior of the classical PSO on 1-D multimodal problem图1 原始PSO算法在一维多峰优化问题上的搜索特性 从图1中可以看到,所有个体都向种群搜索到的历史最优解gbest学习,因此,如果gbest落入局部最优,则其他个体很容易被吸引到局部最优.为了克服这一缺陷,学者们提出了多种更新算子的改进方案.例如Kennedy等人[31]提出了向个体的某个邻域的历史最优解lbest而非gbest学习,得到了基于个体邻域拓扑结构的局部PSO版本;Liang等人[32]和Zhan等人[22]分别提出了分维全面学习和正交学习的PSO算法;Cheng等人[33]针对大规模优化问题,提出了竞争学习的粒子群算法.我们也借鉴自然界中生物的寿命和衰老现象,依托生物学的进化衰老理论,提出了基于寿命的PSO算法[19];同时借鉴竞争策略,我们提出了基于分块的支配学习机制,并引进PSO算法,形成了基于分块支配学习机制的PSO算法[24].类似地,其他基于改进操作算子的新型演化算法如JADE[29],DEEP[17],CMA-ES[34]等也相继被提出. 3) 混合演化算法.由于不同类型的演化算法各具特征,所适合的优化问题也各不相同,部分研究者希望通过结合多种演化算法来提高算法的性能.目前,主要的混合模式包括多策略混合和多算法混合.多策略混合指同一演化算法的多种操作算子相混合,例如多策略混合的DE算法[35-36];多算法混合是指多种演化算法的操作算子相结合,例如基于遗传进化操作的粒子群算法[37]. 1.2 多峰问题的多解演化算法 实际应用中部分优化问题可能具有多个可接受的近似全局最优解,因此优化算法需要发现尽可能多的这些最优解以提供更好的决策支持.与单解优化相比,多解优化要求算法必须具备极高的多样性维持能力,否则算法将很容易落入局部最优或某个全局最优解,而忽略了其他可接受的全局最优解.因此,目前多解优化往往只能采用演化算法进行求解,同时为了进一步提高搜索多样性,在多解优化时必须向演化算法引入特殊的策略.目前主流的2个策略是小生境策略(Niching)和多目标策略(Multi-objective). 1) 小生境策略.小生境策略的核心思想是通过某种技术限制种群中的个体全部向一个方向靠拢.目前主流的小生境策略有:适应值分享策略(fitness sharing)[38]、聚集策略(crowding)[39]以及物种划分策略(speciation)[40]等.为了克服小生境策略对参数的敏感性,基于山谷/山峰检测的小生境策略[41-42]以及基于近邻聚类的小生境策略[43,25]也相继被提出.小生境策略让每个个体在自己附近区域进行搜索,有效地增加了种群的多样性,成为处理多解优化问题的关键技术. 2) 多目标策略.由于多峰问题的多解优化和多目标优化[44]具有一定的近似性,部分学者提出将多峰问题多解优化转化为多目标优化问题进行求解[45-47].一般而言,多峰问题多解优化问题会被转化为双目标优化问题.其中一个目标是多峰优化的目标函数本身,另一个是评价个体位置对搜索空间覆盖度的自定义优化目标.最近,文献[48]结合目标函数和空间分布信息定义出若干个相互冲突的双优化目标,并取得了良好的多解优化效果. 值得一提的是,由于以PSO,DE为代表的基于差值演化操作的演化算法简单而有效,目前大量多峰优化研究都围绕着这类算法展开.对于更复杂的多解问题,现有的工作也几乎围绕将小生境策略或多目标策略与PSO,DE或GA算法相结合而开展.根据汤森路透《2015研究前沿》,PSO,DE等演化算法已经被列为了热点研究前沿.然而,随着峰值个数的增加,特别是在局部最优解众多的多解优化问题上,基于差值演化操作的演化算法仍面临着性能瓶颈,例如在CEC’2013多解优化标准测试函数中,现有的基于DE,PSO等算法的多峰演化算法在部分问题上(特别是包含众多局部最优区域的多峰问题)的全局最优解检出率仍不足20%,甚至为0.此外,由于PSO,DE等算法传统上定义于连续实数向量空间,一般不能直接应用于离散空间的组合优化问题.如何进一步克服算法的搜索多样性问题,突破算法在不同解空间中的可用性瓶颈,仍有待研究. 1.3 分布估计算法 EDA是近年来逐渐受到关注的一类演化算法[18].与DE,PSO等传统演化算法不同的是,该算法没有任何交叉或者变异等操作,而是采用了一种特殊的基于概率分布的种群演化策略.该算法根据当前种群的个体信息,评估种群演化的概率分布信息,并基于该概率分布信息采样产生子代个体.其算法的基本框架如算法2所示. 算法2. EDA算法伪代码. 输入: 种群大小NP、用于分布评估的个体数M、最大迭代次数GEN; 输出: 全局最优解. ① 初始化种群,并评价每个个体的适应值; ②generation=0; ③ While(generation ④ 从种群中选择M个个体,并用这些个体评估种群分布; ⑤ 依据评估的分布模型,采样生成新的个体,并评估新个体的适应值; ⑥ 通过选择产生新的种群,更新全局最优解; ⑦generation++; ⑧ End While 由算法2可以看出,EDA算法的核心在于概率分布的估计,不同的概率分布估计模型衍生出不同的EDA算法.目前,主流的概率分布评估模型有:视所有变量相互独立的单变量模型[49]、将2个变量视为相关变量的双变量模型[50]、将多个变量视为相关变量的多变量模型[51]以及评估每个变量区间个体分布的直方图模型[52]. EDA采用概率分布的思想,具有2个方面的重要优势:1)具有良好的搜索多样性和全局搜索能力.图2给出了EDA算法的搜索特征,即选择种群中部分适应值更高的个体(图2中框内的空心圆点),粗略估计这些优势个体在解空间中的分布概率.与图1所示的PSO等算法的搜索特征相比,EDA能从更宏观的角度评估种群的演化信息,因此往往具有更好的全局性和多样性,不易被个别落入局部最优的个体吸引从而造成早熟收敛现象.2)概率分布统计的方法在连续、离散的解空间中均适用,因此该方法并不受解空间特征的约束.正是这2个方面的优势,基于概率分布的演化算法将为求解多解优化问题提供新的思路,也有助于突破传统上部分演化算法的定义局限于连续实数向量空间的瓶颈. Fig. 2 The search behavior of EDA on 1-D multimodal problem图2 EDA算法在一维多峰优化问题上的搜索特性 如1.3节所述,基于概率的演化算法在保持搜索多样性方面具有优势,然而基于概率分布的演化算法仍没有在搜索多样性要求极高的多解优化等问题中得到研究和应用.针对此,我们在文献[26]中采用传统的概率分布估计算法,提出了多解优化的EDA算法;在文献[27]中进一步利用蚁群优化算法通过信息素释放隐式地建立概率分布的特点,提出了自适应的多解优化ACO算法.本节将从广义的概率分布演化算法的角度,总结出一套多解优化的概率分布演化算法框架,通过将小生境策略与基于概率分布的演化算法相结合,为求解复杂的多峰多解优化问题提供行之有效的新途径,并基于这一框架介绍多解优化的EDA和ACO算法. 2.1 算法框架 基于概率分布的多解优化演化算法的基本思想是将概率分布演化与小生境策略相结合,建立对整个搜索空间中高适应值区域的概率分布估计,从而进一步提高算法的搜索多样性,并结合局部搜索策略保证解的精度.算法框架如图3所示.从图3可以看出,基于概率分布的多解演化算法的整体框架由6个步骤构成: Fig. 3 The framework of the probability distribution-based multimodal algorithms图3 多解优化的概率分布演化算法框架 步骤1. 种群初始化.和其他演化算法一样,该操作随机产生一个分布均匀的初始种群并评价每个个体的适应值. 步骤2. 小生境划分.该操作利用小生境策略将种群划分为若干小生境. 步骤3. 概率分布估计.每个小生境相互独立,因此每个小生境内部的概率分布也相互独立估计.基于每个小生境对应的子种群,评估每个小生境内的演化分布情况.因此,整个种群内包含了多个概率分布模型,对应于解空间中的不同区域. 步骤4. 子代采样.每个小生境根据其评估的概率分布,独立采样得到其新一代的个体,从而使得新一代个体可以分布于解空间的不同区域. 步骤5. 个体选择.每个小生境将子父代个体合并,采用基于近邻的精英选择策略得到新一代种群. 步骤6. 局部搜索.为提高解的精度,对每个小生境内的最好个体,自适应地通过高斯分布进行邻域局部搜索,从而提高解的质量. 上述的步骤2~6反复迭代,直至算法达到终止条件. 在这一框架下,步骤2可以引入不同的小生境策略;步骤3可以选择不同的概率分布估计方法,包括显式的概率分布估计(如EDA显式采用了高斯或柯西分布)或隐式的概率分布估计(如ACO通过信息素隐含地给出了概率分布);步骤5和步骤6中可以引入不同的选择和局部搜索操作.通过这些操作,可以得到不同的基于概率分布的多解演化算法.特别地,该框架将小生境策略和概率分布估计相结合,既保证了搜索个体能覆盖解空间中的不同区域,又对每个小生境内的种群演化信息做出了更全面的概率分布估计,从而从搜索空间整体到小生境内部2个层次提高了算法的搜索多样性;同时,该框架还引入了局部搜索策略,并允许根据实际应用中优化精度的需求调整局部搜索的范围和深度,从而更有利于算法在优化精度和搜索多样性之间取得平衡. 2.2 基于EDA的多解优化算法(MEDA) 在图3的框架下,我们在文献[26]中首次提出了将分布估计算法(EDA)拓展到多峰优化的多解问题,算法的详细伪代码如算法3所示. 算法3. MEDA算法伪代码. 输入: 种群大小NP、分组个数N、局部搜索点数K、最大迭代次数GEN; 输出: 整个种群. ① 初始化种群; ②generation=0; ③ While (generation ④ 将种群划分为N个组,每个组包含M=NPN个个体; ⑤ Fori=1:N ⑦ If(rand(0,1)<0.5)*rand(0,1)产生一个在(0,1)之间的均匀随机数* ⑧ 用柯西分布Cauchy(μ,δ)生成M个新个体; ⑨ Else ⑩ 用高斯分布Gaussian(μ,δ)生成M个新个体; 该算法在每次迭代中首先利用聚类小生境策略将种群划分为若干个小生境(行④),而后对每个小生境独立地进行概率分布估计(行⑥),并根据分布信息采样生成子代个体(行⑦~).子代生成后,不同小生境的子代只和自己对应的小生境父代进行比较,淘汰差的个体(行~),最后通过局部搜索策略提高解的精度(行~).与其他基于小生境策略的多解优化算法及传统EDA算法相比,MEDA算法具有3点新特征: 1) 高斯/柯西相混合的显式概率分布.MEDA采用了显式的概率分布估计方法对每个小生境对应的子种群的演化分布情况进行评估.与以往EDA算法不同的是,MEDA针对多解优化问题的特点,利用小生境策略达到对不同区域的演化信息进行评估,从而使得算法内保持了多个分布信息;并且该算法采用了将柯西分布与高斯分布相结合的方式,通过2种分布二选一的方式来采样生成子代个体,从而利用了高斯分布的强开发能力(exploitation)以及柯西分布的强探索能力(exploration)来平衡算法的多样性和收敛速度. 2) 最近邻替换原则.在将父子两代个体合并筛选出新一代种群的过程中,该算法采用最近邻原则(行)进行个体替换,即适应值更优的个体只替换与其欧几里得距离最近且适应值相对较差的个体,而非如传统EDA算法那样替换掉个体索引号一致或适应值最差的个体.最近邻替换原则能防止个体向同一区域靠拢,使得不同的小生境涵盖了解空间中不同区域的分布信息,从而使得不同小生境内的个体沿着不同的方向搜索解空间,有利于提高搜索多样性,使算法发现解空间中尽可能多的全局最优解. 3) 基于高斯分布的自适应局部搜索.为了克服传统EDA算法局部寻优能力较差、解精度较低的不足,该算法引入了基于高斯分布的局部搜索方法,对每个小生境内的种子个体(即该小生境内最好的个体)根据其适应值自适应进行局部搜索,从而使算法能用较少的适应值评价次数获取精度更高的最优解. 文献[26]的实验结果也表明,该算法能够比以往多峰算法,特别是基于PSO,DE等基于差值操作的多峰演化算法能够发现更多的全局最优解.例如在共有20个多解优化问题的CEC’2013测试集上,MEDA算法能够在12个测试函数上发现更多的全局最优解.特别地,在包含众多局部最优点的多峰问题如f20上,MEDA算法将全局最优解的检出率从0%提高到24.8%.这些实验结果证明MEDA算法具有更强的多样性,而且能够更好地平衡算法多样性和收敛速度. 2.3 基于自适应ACO的多解优化算法(AM-ACO) 除了显式采用概率分布的EDA算法之外,部分演化算法的进化过程也蕴含了概率分布的思想.例如,蚁群优化算法(ACO)是一类重要的群体智能算法,其核心思想是模拟蚂蚁群体在寻找食物过程中在路径上释放信息素,并通过感知路径的信息素积累来发现最短路径.ACO已在众多组合优化问题中展现出了良好的性能[53].由于ACO的信息素历史积累,本质上可以理解成一种特殊的概率分布,拓展至连续空间的ACO算法版本,即ACOR算法[54]更具有明显的概率分布特征,因此我们将ACO理解成一类广义的基于概率分布的演化算法.与EDA不同,ACO的信息素是以每个个体的位置为中心,根据个体适应值的好坏而正相关地释放并向外扩散,因此如果种群能覆盖多个峰值所在的区域,其构建的信息素分布可以同时刻画出多个峰值所对应的解空间分布特征,从而有助于进一步提高算法的搜索多样性.受此启发,我们在文献[27]首次将ACO拓展至多峰问题多解优化,提出了自适应的多峰蚁群算法(AM-ACO),其伪代码如算法4所示. 算法4. AM-ACO算法伪代码. 输入: 种群大小NP、文档集大小NP、分组个数N、局部搜索点数K、最大迭代次数GEN; 输出: 整个种群. ① 初始化文档集; ②generation=0; ③ While(generation ④ 将文档集划分为N个组,每个组包含M=NPN个个体; ⑤ 获得文档集的最大和最小适应值:FSmax,FSmin; ⑥ Fori=1:N 在如图3所示的基于概率分布的多解演化算法框架下,AM-ACO仍采用聚类小生境策略将种群进行划分为小生境(行④),随后基于ACO的进化模式对每个小生境分别构建子代解(行~).在种群更新方面,该算法仍采取最近邻替换策略进行种群更新(行),并利用基于高斯分布的自适应局部搜索算法(行~)提高解的精确度.特别地,AM-ACO算法有如下的新特点: Fig. 4 The framework of the probability-based discrete evolutionary algorithms based on set operations图4 基于概率的集合型离散演化算法框架 1) 基于蚁群优化模式的解构建.与EDA的概率分布估计方法不同,AM-ACO算法根据小生境内每个个体的适应值,计算每个个体释放的信息素,对应于该个体的邻域被选择用于构建子代解的概率分布(行⑨⑩).根据这一概率,选择个体并在其邻域或邻域的变异区域内基于高斯分布采样生成新的子代解(行~). 2) 自适应控制参数.对构造概率分布中的关键控制参数σ,该算法提出了一种自适应调整策略(行⑧).该策略将小生境间个体的差异以及小生境内个体的差异同时考虑在内,使得不同的小生境有不同的σ,从而使得ACO算法摆脱了对参数σ的敏感性和依赖性. 通过将小生境策略、基于ACO的解构建策略和σ的自适应调整策略相结合,AM-ACO算法能够既在各个小生境层面上均匀地演化,又能使每个小生境内的解分布于不同的区域,沿着不同方向进化;基于高斯分布的子代解生成和局部搜索策略还能进一步提高搜索的速度和解的精度,因此AM-ACO算法具有良好的搜索多样性和收敛速度.文献[27]的实验结果也表明,该算法能够在CEC’2013多解优化测试集上能较MEDA进一步提高多解优化的性能.特别地,在包含众多局部最优解的多峰问题如f20上,基于概率分布的演化算法能将全局最优解的检出率从原有其他经典方法的0%,到MEDA的24.8%,再到AM-ACO的34.6%.这些实验结果证明了基于概率分布的演化算法在求解复杂的多峰多解优化问题时,在保持算法的搜索多样性和提高全局最优解的检出率方面具有明显的优势. 基于概率分布的演化方式的另一优势是能通用于连续和离散空间的决策变量.因此,针对PSO等定义于连续实数向量空间的演化算法无法直接应用于离散组合优化的瓶颈,我们受基于概率分布的演化方式的启发,在文献[1]提出了基于集合论和概率分布的集合型离散演化算法框架,将PSO等算法拓展至离散空间.该算法框架如图4所示. 为了将形如式(1)(2)的PSO等算法的演化操作在离散空间中拓展,集合型框架主要包含了4个特征: 1) 集合型解表示.集合是表示离散变量的一般方法.因此,该框架采用集合的方式来表示离散决策变量.例如,在旅行商问题中,问题的一个解(即遍历所有点一次且仅一次并返回出发点的哈密顿圈)可以由这条路径所包含的边的集合来表示.如图4所示,路径1—2—3—4—1的表示方式是集合X={(1,2),(2,3),(3,4),(1,4)}. 2) 学习概率表示.除了解的表示之外,式(1)(2)还含有另一类型的变量——速度,表示个体在更新时将要移动的方向和距离.在连续空间中,速度仍可以通过连续实数向量表示.为了在离散空间中定义相应类型的变量,借鉴概率操作,我们将速度定义为一个带概率的集合.在图4的例子中,V={(1,2)/0.8,(1,4)/0.2,(3,4)/0.5,(4,5)/0.3,(5,6)/0.1}定义了一个速度变量,其含义是个体更新时将要学习的元素及其概率.例如,集合V中含有(1,2)/0.8,表示个体将有80%的概率向元素(1,2)(即旅行商问题中(1,2)这条边)学习来产生新的子代解.这样,速度集合V事实上定义了一个值得个体用于学习和更新子代的元素的概率分布. 3) 学习概率更新.如式(1)的基于差值运算的演化操作的一个重要特征是:通过求2个解的差值,一方面得到了当前个体向种群的占优个体学习的方向,从而引导个体向种群占优个体的方向学习和移动;另一方面得到了搜索的邻域范围,使算法能在优势个体的邻域范围内进一步寻优,得到精度更高的解.利用上述基于学习概率表示的速度定义,式(1)定义的基于差值运算的速度更新过程,可以在离散几何空间中重定义,如图4的“速度更新”步骤所示.在这一速度更新步骤中,差值运算可以定义为2个解的集合差运算,其意义是找到那些存在于优势解(例如种群的历史最优解GBest集合)而不在个体当前解(即集合X)的那些元素,将这些元素列为值得学习的元素.此外,参数×集合的运算可以定义为将该参数作为集合中所有元素的被学习概率(定义于区间[0,1]),2个带概率的集合的求和运算则定义为这2个集合的并集,若某元素同时出现在2个集合中则取其概率更高的一项.这样,传统上在连续实数空间的差值演化运算,就能够在集合空间中重定义,并且运算的意义是一致的,即发现当前个体X值得向占优个体(例如GBest)学习的地方,并且以一定的概率进行学习. 4) 位置更新.根据上述更新操作得到的速度Vi,个体Xi将按照Vi所给出的值得学习的元素及其学习概率更新个体的位置,产生子代个体.如图4所示,为了使产生的新个体能够满足问题的约束条件,可选用的解更新策略有2类:①逐步构建策略,即从Xi的某个元素开始,在满足约束条件的前提下,根据学习概率或者选择Vi中值得学习的元素,或者仍然采用原有个体Xi中的相应元素,不断添加元素直至构建出整体可行解为止.例如在旅行商问题中,可以从某个城市出发,逐步向子代解的集合中添加边,直至完整地构建出一个哈密顿圈.②整体构建和解修补策略,即先根据速度Vi和当前解Xi按概率合并得到一个新的解,再通过解的修补策略保证该解能够满足问题的约束条件.例如在背包问题中,可以将从Vi中根据概率选出的物品和Xi中原有的物品全部选择,再通过特定的解修补策略从中删除部分物品直至所构造的解满足背包的容量约束. 通过上述的4个特征,基于概率的集合型演化算法框架将PSO等基于实数差值运算的演化算法在集合空间中重定义,从而将算法从连续空间拓展至离散空间,提高算法在不同解空间中的可用性.特别地,该框架借助概率分布的思想,将引导个体更新的速度变量定义为待学习元素的概率分布,具有3点优势[1]: 1) 该框架中定义的离散空间中的差值运算与连续空间中传统PSO等算法的差值运算的意义一致,从而能够在离散空间中保留了PSO等算法原有的搜索行为和特征; 2) 由于搜索行为一致,传统PSO等算法的控制参数作用和设定,在基于概率和集合的离散算法框架中仍然有效; 3) 各种改进版本的PSO等算法以及其他基于实数向量差值运算的演化算法版本,都能够根据这一框架拓展成相应的离散版本. 目前,基于这一框架的离散演化算法已被成功地应用在旅行商问题[1]、多重背包问题[1]、车辆路由优化问题[6]、软件测试覆盖集生成问题[55],并展现出了良好的性能和应用前景. 本文围绕多峰优化难题,对多峰优化的演化算法发展进行了概述.特别地,一类新兴的演化算法——分布估计算法(EDA),其基于概率分布估计的演化方式在搜索多样性和连续、离散解空间中的通用性都具有优势.受此启发,我们提出了2个基于概率分布的演化算法框架,即多解优化的概率分布演化算法框架和基于概率的集合型离散演化算法框架.前者从更广义的角度理解基于概率分布的演化操作,并将其推广应用于复杂的多解优化问题,有效地提高了算法的搜索多样性,提高了全局最优解的检出率;后者将集合表示方式和概率分布思想相结合,实现了将PSO等算法从连续实数向量空间到离散空间的重定义,并保留了算法的搜索行为特征,为求解多峰的组合优化问题提供新的有效途径. 基于概率分布的演化算法已经在多类复杂优化问题中体现了良好的优化性能,然而相比于以PSO,DE为代表的基于差值操作的演化算法,该类演化算法发展相对缓慢,仍有很大发展空间.结合基于概率分布的演化算法的特征,我们认为这类算法将在如下的复杂优化问题上有重要的发展和应用前景: 1) 大规模优化.目前大多数演化算法只能有效处理低维空间的多峰优化问题,然而当面对高维度优化问题时,这些演化算法的性能大大降低,面临着“维度诅咒”.一方面,随着维度的增长,问题的解空间呈几何式爆炸增长,极大地挑战着目前演化算法的搜索效率;另一方面,随着维度的增长,多峰问题解空间中的局部最优点往往也呈爆炸式增长,使得目前演化算法陷入局部最优的可能性大大增加.为处理以上问题:①需要增加演化算法的多样性;②需要保持演化算法的收敛速度[56-57].如第2节和第3节所述,由于基于概率分布的演化算法在搜索多样性和全局性上具有显著的优势,这类算法和局部搜索方法的有机结合将有望能为突破大规模优化的性能瓶颈提供新的有效途径. 2) 不确定性优化.随着大数据时代的到来,大量优化问题都呈现出不确定性,即待解问题的环境变量也是通过一定的概率分布给出,而非确定性给出.例如项目管理优化中企业的现金流状况、物流交通优化中当前路网的车流状况,这些环境变量往往都是不可在优化前确定预知的,这些不确定性大大增加了优化问题的求解难度,成为了优化领域的研究前沿难题.由于基于概率分布的演化算法的核心思想就是构建概率分布模型,这与基于概率的不确定性描述方式是相一致的.因此,基于概率分布的演化算法在求解带不确定性的优化问题上具有广阔的发展潜力. 3) 实际应用.相对于基于概率分布的演化算法本身的发展,其实际应用还仅限于传统的低维度的类TSP问题[58]以及调度类优化问题[7-8,59-60].然而,随着大数据时代的到来,实际生活以及工业生产产生的多峰优化问题愈发常见.因此,推广该类演化算法在如网络检测[5]、行人识别[61]等大数据领域中的应用也是日后发展演化算法的热点之一. [1]Chen Weineng, Zhang Jun, Chung H S H, et al. A novel set-based particle swarm optimization method for discrete optimization problems[J]. IEEE Trans on Evolutionary Computation, 2010, 14(2): 278-300 [2]Xue Bing, Zhang Mengjie, Browne W N, et al. A survey on evolutionary computation approaches to feature selection[J]. IEEE Trans on Evolutionary Computation, 2016, 20(4): 606-626 [3]Jun Zhang, Chung H S H, Lo W L. Pseudocoevolutionary genetic algorithms for power electronic circuits optimization[J]. IEEE Trans on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2006, 36(4): 590-598 [4]Gong Yuejiao, Shen Meie, Zhang Jun, et al. Optimizing RFID network planning by using a particle swarm optimization algorithm with redundant reader elimination[J]. IEEE Trans on Industrial Informatics, 2012, 8(4): 900-912 [5]Wen Xuyun, Chen Weineng, Lin Ying, et al. A maximal clique based multiobjective evolutionary algorithm for overlapping community detection[J]. IEEE Trans on Evolutionary Computation, DOI: 10.1109/TEVC.2016.2605501 [6]Gong Yuejiao, Zhang Jun, Liu Ou, et al. Optimizing the vehicle routing problem with time windows: A discrete particle swarm optimization approach[J]. IEEE Trans on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2012, 42(2): 254-267 [7]Chen Weineng, Zhang Jun. An ant colony optimization approach to a grid workflow scheduling problem with various QoS requirements[J]. IEEE Trans on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2009, 39(1): 29-43 [8]Chen Weineng, Zhang Jun. Ant colony optimization for software project scheduling and staffing with an event-based scheduler[J]. IEEE Trans on Software Engineering, 2013, 39(1): 1-17 [9]Hruschka E R, Campello R J G B, Freitas A A, et al. A survey of evolutionary algorithms for clustering[J]. IEEE Trans on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2009, 39(2): 133-155 [10]Barros R C, Basgalupp M P, de Carvalho A C P L F, et al. A survey of evolutionary algorithms for decision-tree induction[J]. IEEE Trans on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2012, 42(3): 291-312 [11]Zhang Jun, Zhan Zhihui, Lin Ying, et al. Evolutionary computation meets machine learning: A survey[J]. IEEE Computational Intelligence Magazine, 2011, 6(4): 68-75 [12]Eiben A E, Smith J. From evolutionary computation to the evolution of things[J]. Nature, 2015, 521(7553): 476-482 [13]Srinivas M, Patnaik L M. Genetic algorithms: A survey[J]. Computer, 1994, 27(6): 17-26 [14]Gustafson S, Vanneschi L. Crossover-based tree distance in genetic programming[J]. IEEE Trans on Evolutionary Computation, 2008, 12(4): 506-524 [15]Francois O. An evolutionary strategy for global minimization and its Markov chain analysis[J]. IEEE Trans on Evolutionary Computation, 1998, 2(3): 77-90 [16]Yao Xin, Liu Yong, Lin Guangming. Evolutionary programming made faster[J]. IEEE Trans on Evolutionary Computation, 1999, 3(2): 82-102 [17]Li Yuanlong, Zhan Zhihui, Gong Yuejiao, et al. Differential evolution with an evolution path: A DEEP evolutionary algorithm[J]. IEEE Trans on Cybernetics, 2015, 45(9): 1798-1810 [18]Hauschild M, Pelikan M. An introduction and survey of estimation of distribution algorithms[J]. Swarm and Evolutionary Computation, 2011, 1(3): 111-128 [19]Chen Weineng, Zhang Jun, Lin Ying, et al. Particle swarm optimization with an aging leader and challengers[J]. IEEE Trans on Evolutionary Computation, 2013, 17(2): 241-258 [20]Dorigo M, Birattari M, Stützle T. Ant colony optimization[J]. IEEE Computational Intelligence Magazine, 2006, 1(4): 28-39 [21]Zhan Zhihui, Zhang Jun, Li Yun, et al. Adaptive particle swarm optimization[J]. IEEE Trans on Systems, Man, and Cybernetics, Part B (Cybernetics), 2009, 39(6): 1362-1381 [22]Zhan Zhihui, Zhang Jun, Li Yun, et al. Orthogonal learning particle swarm optimization[J]. IEEE Trans on Evolutionary Computation, 2011, 15(6): 832-847 [23]Li Yuanlong, Zhan Zhihui, Gong Yuejiao, et al. Fast micro-differential evolution for topological active net optimization[J]. IEEE Trans on Cybernetics, 2016, 46(6): 1411-1423 [24]Yang Qiang, Chen Weineng, Gu Tianlong, et al. Segment-based predominant learning swarm optimizer for large-scale optimization[J]. IEEE Trans on Cybernetics, DOI: 10.1109/TCYB.2016.2616170 [25]Gao Weifeng, Yen G G, Liu Sanyang. A cluster-based differential evolution with self-adaptive strategy for multimodal optimization[J]. IEEE Trans on Cybernetics, 2014, 44(8): 1314-1327 [26]Yang Qiang, Chen Weineng, Li Yun, et al. Multimodal estimation of distribution algorithms[J]. IEEE Trans on Cybernetics, 2017, 47(3): 636-650 [27]Yang Qiang, Chen Weineng, Yu Zhengtao, et al. Adaptive multimodal continuous ant colony optimization[J]. IEEE Trans on Evolutionary Computation, 2017, 21(2): 191-205 [28]Streifel R J, Marks R J, Reed R, et al. Dynamic fuzzy control of genetic algorithm parameter coding[J]. IEEE Trans on Systems, Man, and Cybernetics, Part B (Cybernetics), 1999, 29(3): 426-433 [29]Zhang Jingqiao, Sanderson A C. JADE: Adaptive differential evolution with optional external archive[J]. IEEE Trans on Evolutionary Computation, 2009, 13(5): 945-958 [30]Tang Lixin, Dong Yun, Liu Jiyin. Differential evolution with an individual-dependent mechanism[J]. IEEE Trans on Evolutionary Computation, 2015, 19(4): 560-574 [31]Kennedy J, Mendes R. Population structure and particle swarm performance[C] //Proc of IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2002, 3: 1-1962 [32]Liang Jing, Qin A Kai, Suganthan P N, et al. Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J]. IEEE Trans on Evolutionary Computation, 2006, 10(3): 281-295 [33]Cheng Ran, Jin Yaochu. A competitive swarm optimizer for large scale optimization[J]. IEEE Trans on Cybernetics, 2015, 45(2): 191-204 [34]Hansen N. The CMA evolution strategy: A comparing review[C] //Towards a New Evolutionary Computation: Advances in the Estimation of Distribution Algorithms. Berlin: Springer, 2006: 75-102 [35]Wang Yong, Cai Zixing, Zhang Qingfu. Differential evolution with composite trial vector generation strategies and control parameters[J]. IEEE Trans on Evolutionary Computation, 2011, 15(1): 55-66 [36]Hu Mengqi, Wu T, Weir J D. An adaptive particle swarm optimization with multiple adaptive methods[J]. IEEE Trans on Evolutionary Computation, 2013, 17(5): 705-720 [37]Gong Yuejiao, Li Jingjing, Zhou Yicong, et al. Genetic learning particle swarm optimization[J]. IEEE Trans on Cybernetics, 2016, 46(10): 2277-2290 [38]Goldberg D E, Richardson J. Genetic algorithms with sharing for multimodal function optimization[C] //Proc of the 2nd Int Conf on Genetic Algorithms. Hillsdale, NJ: Lawrence Erlbaum, 1987: 41-49 [39]Thomsen R. Multimodal optimization using crowding-based differential evolution[C] //Proc of IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2004, 2: 1382-1389 [40]Li Xiaodong. Efficient differential evolution using speciation for multimodal function optimization[C] //Proc of the 7th Annual Conf on Genetic and Evolutionary Computation. New York: ACM, 2005: 873-880 [41]Ursem R K. Multinational GAs: Multimodal optimization techniques in dynamic environments[C] //Proc of the 2nd Annual Conf on Genetic and Evolutionary Computation. San Francisco, CA: Morgan Kaufmann, 2000: 19-26 [42]Li Lingxi, Tang Ke. History-based topological speciation for multimodal optimization[J]. IEEE Trans on Evolutionary Computation, 2015, 19(1): 136-150 [43]Qu Boyang, Suganthan P N, Liang Jing. Differential evolution with neighborhood mutation for multimodal optimization[J]. IEEE Trans on Evolutionary Computation, 2012, 16(5): 601-614 [44]Chen Ni, Chen Weineng, Gong Yuejiao, et al. An evolutionary algorithm with double-level archives for multiobjective optimization[J]. IEEE Trans on Cybernetics, 2015, 45(9): 1851-1863 [45]Yao Jie, Kharma N, Grogono P. Bi-objective multipopulation genetic algorithm for multimodal function optimization[J]. IEEE Trans on Evolutionary Computation, 2010, 14(1): 80-102 [46]Deb K, Saha A. Multimodal optimization using a biobjective evolutionary algorithm[J]. Evolutionary Computation, 2012, 20(1): 27-62 [47]Basak A, Das S, Tan K C. Multimodal optimization using a biobjective differential evolution algorithm enhanced with mean distance-based selection[J]. IEEE Trans on Evolutionary Computation, 2013, 17(5): 666-685 [48]Wang Yong, Li Hanxiong, Yen G G, et al. MOMMOP: Multiobjective optimization for locating multiple optimal solutions of multimodal optimization problems[J]. IEEE Trans on Cybernetics, 2015, 45(4): 830-843 [49]Bosman P, Thierens D. Expanding from discrete to continuous estimation of distribution algorithms: The IDEA[C] //Proc of the 6th Int Conf on Parallel Problem Solving from Nature. Berlin: Springer, 2000: 767-776 [51]Mühlenbein H, Mahnig T. FDA-a scalable evolutionary algorithm for the optimization of additively decomposed functions[J]. Evolutionary Computation, 1999, 7(4): 353-376 [52]Mühlenbein H, Paaß G. From recombination of genes to the estimation of distributions I. binary parameters[C] //Proc of the 4th Int Conf on Parallel Problem Solving from Nature. Berlin: Springer, 1993: 178-187 [53]Dorigo M, Stützle T. Ant Colony Optimization[M]. Cambridge, MA: MIT Press, 2004 [54]Socha K, Dorigo M. Ant colony optimization for continuous domains[J]. European Journal of Operational Research, 2008, 185(3): 1155-1173 [55]Wu Huayao, Nie Changhai, Kuo Feiching, et al. A discrete particle swarm optimization for covering array generation[J]. IEEE Trans on Evolutionary Computation, 2015, 19(4): 575-591 [56]Yang Qiang, Xie Hanyu, Chen Weineng, et al. Multiple parents guided differential evolution for large scale optimization[C] //Proc of 2016 IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2016: 3549-3556 [57]Song An, Yang Qiang, Chen Weineng, et al. Random-based dynamic grouping strategy for large scale multi-objective optimization[C] //Proc of 2016 IEEE Congress on Evolutionary Computation. Piscataway, NJ: IEEE, 2016: 468-475 [58]Yu Xue, Chen Weineng, Hu Xiaomin, et al. A set-based comprehensive learning particle swarm optimization with decomposition for multiobjective traveling salesman problem[C] //Proc of the 2015 Annual Conf on Genetic and Evolutionary Computation. New York: ACM, 2015: 89-96 [59]Chen Weineng, Zhang Jun, Chung H S H, et al. Optimizing discounted cash flows in project scheduling—an ant colony optimization approach[J]. IEEE Trans on Systems, Man, and Cybernetics, Part C (Applications and Reviews), 2010, 40(1): 64-77 [60]Liu Yu, Chen Weineng, Hu Xiaomin, et al. An ant colony optimizing algorithm based on scheduling preference for maximizing working time of WSN[C] //Proc of the Annual Conf on Genetic and Evolutionary Computation. New York: ACM, 2015: 41-48 [61]Chen Ni, Chen Weineng, Zhang Jun. Fast detection of human using differential evolution[J]. Signal Processing, 2015, 110: 155-163 Chen Weineng, born in 1983. PhD, professor and PhD supervisor. Member of CCF. His main research interests include swarm intelligence algorithms and their applications on cloud computing, operations research and software engineering. Yang Qiang, born in 1988. PhD candidate and research assistant. His main research interests include evolutionary algorithms and their applications on real-world problems. Probability Distribution Based Evolutionary Computation Algorithms for Multimodal Optimization Chen Weineng1and Yang Qiang1,2 1(SchoolofComputerScienceandEngineering,SouthChinaUniversityofTechnology,Guangzhou510006) Evolutionary computation (EC) is a category of algorithms which simulate the intelligent evolutionary behavior in nature for solving optimization problems. As EC algorithms do not rely on the mathematical characteristics of the problem model, they have been regarded as an important tool for complex optimization. Estimation of distribution algorithm (EDA) is a new class of EC algorithms, which works by constructing a probability model to estimate the distribution of the predominant individuals in the population, and sampling new individuals based on the probability model. With this probability-based search behavior, EDA is good at maintaining sufficient search diversity, and is applicable in both continuous and discrete search space. In order to promote the research of probability-based EC (PBEC) algorithms, this paper gives a survey on EC algorithms for multimodal optimization, and then further builds two frameworks for PBEC: PBEC framework for seeking multiple solutions in multimodal optimization, and PBEC framework for discrete optimization. The first framework presents a method to combine probability-based evolutionary operators with the niching strategy, so that higher search diversity can be maintained for seeking multiple solutions in multimodal optimization. In particular, the framework understands PBEC algorithms in a broad sense, that is, it allows both explicit PBEC algorithms (e.g. EDA) and implicit PBEC algorithms (e.g. ant colony optimization) to operate in the framework, resulting in two representative algorithms: multimodal EDA (MEDA) and adaptive multimodal ant colony optimization (AM-ACO). The second framework aims at extending the applicability of EC algorithms on both continuous and discrete space. Since some popular EC algorithms are originally defined on continuous real vector space and they cannot be directly used to solve discrete optimization problems, this framework introduces the idea of probability distribution based evolution and redefines their evolutionary operators on discrete set space. As a result, the applicability of these algorithms can be significantly improved. probability distribution; evolutionary algorithm (EA); evolutionary computation (EC); multimodal optimization; computational intelligence 2016-11-24; 2017-03-31 国家自然科学基金优秀青年科学基金项目(61622206);国家自然科学基金面上项目(61379061) This work was supported by the National Natural Science Foundation of China for Excellent Yong Scientists (61622206) and the General Program of the National Natural Science Foundation of China (61379061). TP3-0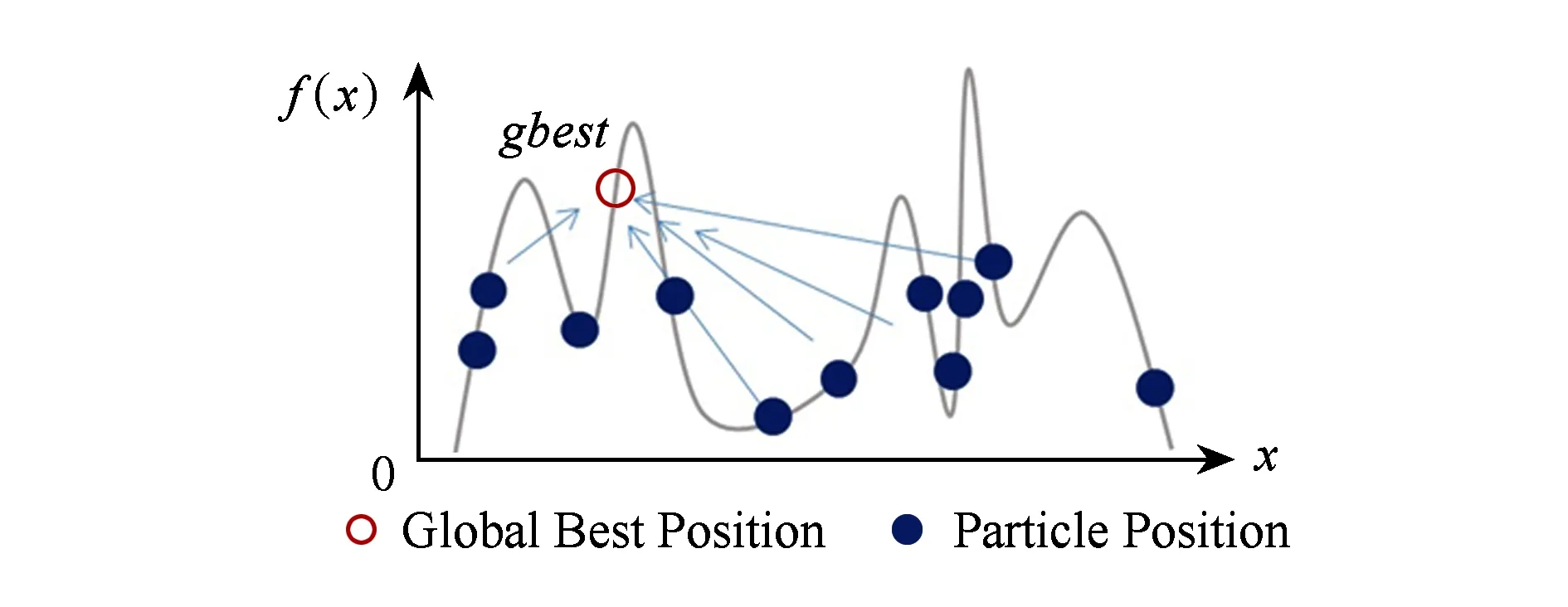
2 多解优化的概率分布演化算法框架
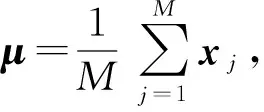
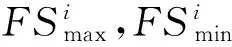
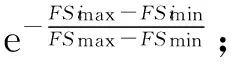
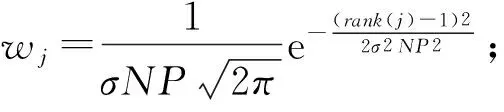
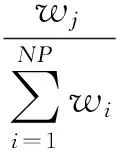
3 基于概率的集合型离散演化算法框架
4 总结与展望


