六盘山华北落叶松林下穿透雨空间变异特征

刘泽彬,王彦辉,*,邓秀秀,刘 宇,张 桐,左海军,王亚蕊,熊 伟,于澎涛,徐丽宏

1 中国林业科学研究院森林生态环境与保护研究所,国家林业局森林生态环境重点实验室, 北京 100091 2 中南林业科技大学林学院, 长沙 410004 3 北京林业大学水土保持学院, 北京 100083



六盘山华北落叶松林下穿透雨空间变异特征

刘泽彬1,王彦辉1,*,邓秀秀2,刘 宇3,张 桐3,左海军1,王亚蕊1,熊 伟1,于澎涛1,徐丽宏1

1 中国林业科学研究院森林生态环境与保护研究所,国家林业局森林生态环境重点实验室, 北京 100091 2 中南林业科技大学林学院, 长沙 410004 3 北京林业大学水土保持学院, 北京 100083

受林冠截持影响后形成的林下穿透雨的数量和空间分布会影响林地的入渗、产流、蒸发等水文过程和林木生长及枯落物分解等生态过程,因而精细的森林水文功能评价和森林生态系统经营都需要准确描述林下穿透雨的空间变异规律。在宁夏六盘山香水河小流域设立了面积为30 m×30 m的华北落叶松人工林样地,均匀布设了40个截面面积230.58 cm2的雨量收集器,测定了2015年生长季(5—10月)34次降雨事件的穿透雨量。结果表明,研究期间林外总降雨量567.0 mm,林下总穿透雨量483.5 mm,占同期雨量的85.3%。随着次降雨量增加,林内次穿透雨率呈现先快速增加后趋于稳定的变化。穿透雨量在林内存在较大空间变异,其变异程度随次降雨量增加先快速下降后趋于稳定。林下穿透雨空间分布受树木特征(穿透雨收集器上方的林冠叶面积指数和冠层厚度、穿透雨测点离最近树干的距离)的影响,且其影响随次降雨量大小而变,当次降雨量<10 mm时,穿透雨量与叶面积指数显著负相关；当次降雨量在10—20 mm时,穿透雨量与距最近树干距离显著正相关,与冠层厚度显著负相关；当次降雨量>20 mm时,穿透雨量与3个树木特征均不显著相关。考虑到研究区次降雨量集中在0—10 mm,在95%或90%的置信区间下,若将测定的次穿透雨数值误差控制在10%以内时,在30 m×30 m样地内至少需布设13或9个本研究所用大小的收集器；满足次穿透雨数值误差在5%以内时,至少需布设26或23个这样的收集器。

华北落叶松；穿透雨；空间变化；Monte Carlo模拟

降雨经过林冠后一部分被截留,一部分转化为干流,其余部分则以穿透雨形式进入地表。由于林冠的截留量有限以及干流量仅占降雨量很小一部分,因此穿透雨往往成为林地水分补给的主要形式[1- 2]；同时,穿透雨可以湿沉降形式把大气中漂浮物及林冠截持物和林冠淋溶物洗脱后输入到林地,因而也是林地养分输入的重要途径[3- 4]。林冠特征的空间差异及其截持作用,导致穿透雨的数量和空间分布变化很大,这对于林地的入渗、产流、蒸发等一系列生态水文过程和土壤水分空间分布及养分循环等均具有重要影响。对此进行准确描述,是开展精细化的森林生态水文影响评价和森林生态系统经营的需要。

国内外已对森林穿透雨特征做了大量研究,研究测定方法主要是在林地布设雨量收集器,涉及到穿透雨的数量变化[5- 7]、时空格局、影响因素[8- 10],以及穿透雨收集器数量对测定精度的影响[1,11]等,取得了较丰硕成果,如Sinnun等[12]和曹云等[13]均报道,冠层对降雨的聚集效应可能会使局部穿透雨量大于林外雨量；Wullaert等[8]和时忠杰等[14]研究认为,冠层结构(如叶面积指数、冠层厚度、郁闭度等)是影响穿透雨空间分布的重要因素；Shinohara等[1]研究发现,穿透雨收集器布设数量达8个以上时才能保证毛竹林(Phyllostachyspubescens)穿透雨测定误差在可接受范围内。这些研究成果为进一步深入研究森林水文过程和水量平衡影响等奠定了良好基础。

华北落叶松(Larixprincipis-ruprechtii)是我国北方地区的主要造林树种之一,其水文服务功能在很多地区都很重要[15- 17]。目前华北落叶松林冠水文作用研究已较多,涉及到降雨组分变化[18]、截留特征[19]、单株林冠下穿透雨空间变化[20]等。但在林分尺度上还缺乏对穿透雨空间分布特征的研究。因此,本文在宁夏六盘山香水河小流域,选择了华北落叶松人工林样地,布设40个穿透雨收集器,进行了一个生长季的监测,详细探讨穿透雨的空间分布特征及影响因素,并合理确定穿透雨收集器的布设数量,以期为准确量化华北落叶松林降水转化作用及开展水文调节功能评价提供科学依据。

1 研究区概况与研究方法

1.1 研究区概况

图1 研究区1961—2010年月均降雨量和月均气温分布 Fig.1 Distribution of the mean monthly precipitation and air temperature at study area in 1961—2010

研究区位于宁夏回族固原六盘山自然保护区南侧的香水河小流域(106°09′—106°30′E,35°15′—35°41′N,海拔2010—2942 m),属暖温带半湿润气候,年均气温6.0℃,年均降水量632 mm,5—10月降雨量占全年降雨量的87.1%(图1),无霜期100—130 d[21]。小流域内土壤以山地灰褐土为主。小流域面积为43.74 km2,其森林覆盖率高达70%,以天然次生林为主,主要树种有华山松(Pinusarmandii)、红桦(Betulaalbo-sinensis)、白桦(Betulaplatyphylla)和辽东栎(Quercusliaotungensis)等；人工林占有较高面积比例,达31.3%,以华北落叶松林为主,另有少量油松(Pinustabuliformis)林等。

在香水河小流域的分水岭沟子流域,设置了一块30 m×30 m 华北落叶松人工纯林样地,其海拔高度为2410 m,坡向为东南坡,平均坡度为21°。林冠郁闭度为0.73,林下灌木稀少,覆盖度在5%左右,有蒙古荚迷(Viburnummongolicum)、秦岭小檗(Berberiscircumserrata)等；草本覆盖度在40%左右,以东方草莓(Fragariaorientalis)和华北苔草(Carexhancockiana)为优势种。样地具体林分结构特征详见表1。

表1 华北落叶松样地林分特征

1.2 降雨及穿透雨测定

在离样地100 m的空旷地,放置一台WeatherHawk 232自动气象站(WeatherHawk,USA),测定林外降水量,每隔5 min记录1次数据。同时在附近放置1个直径20 cm的标准雨量筒,作为备用和修正。

为准确地反映林内穿透雨的空间分布特征,采用林内网格机械布点和随机布点相结合的方法布设穿透雨收集器,即首先按6 m×6 m网格间距布设36个自制穿透雨收集器,然后再随机布设4个穿透雨收集器,共40个。穿透雨收集器的截面积为230.58 cm2(长18.3 cm,宽12.6 cm),其上端截面高出地面25 cm,以避免草本植物和地面雨滴击溅的影响。同时,利用卷尺测定各雨量收集器距最近一棵树树干的距离。每次降雨结束后,立即用量筒测定各收集器中的穿透雨体积(mL),并换算成雨深(mm)。在2015年生长季(5—10月),共测定了34场有效降雨事件(即能收集到穿透雨的降雨事件)。

1.3 叶面积指数和冠层厚度测定

于2015年6—8月,利用LAI- 2200C冠层分析仪(LI-COR,USA),测定每个雨量收集器正上方的叶面积指数,测定时间为每月中旬。由于该地区降雨多集中在6—8月份,且6月中旬后的叶面积指数已基本稳定,因此利用这3个月的实测叶面积指数平均值反映各雨量收集器上方的叶面积指数特征。利用VertexⅢ超声波测高测距仪(Häglof,Sweden),测定每个雨量收集器上方的冠层厚度。

1.4 穿透雨收集器数目的确定

利用Monte Carlo模拟重抽样的方法[11],确定一定误差范围下所需的雨量收集器最少数量。具体做法如下：(1)将2015年5—10月34场降雨分为3个降雨量级(0—10、10—20、>20 mm),将每个雨量级下40个穿透雨收集器所测定穿透雨深的平均值作为Monte Carlo模拟的初始值。(2)利用Monte Carlo模拟重抽样方法,对雨量筒(n=2—39)进行多次重抽样(不放回抽样),重抽样过程重复1000次,以获取足够的随机样本[1,11],计算不同组的n个雨量收集器的穿透雨平均值,这一过程可保证从固定的40个雨量收集器中随机模拟可能出现的2—39个雨量收集器的平均值。(3)对不同数量(n=2—39)的雨量收集器,计算得到平均穿透雨量的分布特征和范围,同时也可取平均值的置信区间[11]。然后,根据平均穿透雨量平均值及其置信区间随雨量收集器数量的变化,就可得出在一定误差水平下每个降雨量级所需的雨量收集器最少数量。

1.5 统计分析

利用SPSS 19.0软件中的Pearson相关性分析,揭示穿透雨量与叶面积指数、冠层厚度和测点离开树干距离的关系。利用R 3.2.3软件,进行Monte Carlo重抽样模拟。利用SigmaPlot 11.0软件,进行绘图。

2 结果与分析

2.1 研究期间降雨特征

在研究期间(2015年5月6日—10月31日)共观测到能产生穿透雨的有效降雨事件34次,对应的林外累计降雨量为567.0 mm,平均次降雨量16.8 mm,变异系数为101.4%。研究期间的次降雨量集中在0—10 mm之间,发生频率达50.9%；降雨量级在10—40 mm之间的降雨发生频率为40.2%；>40 mm的降雨发生频率较低,仅8.8%(图2)。

研究期间平均降雨历时变异较大,从0.5 h到48 h,平均为11.0 h,变异系数可达122.9%。次降雨历时主要集中在0—20 h 之间,占85.3%,其中≤2 h的降雨发生频率占26.5%；降雨历时>20 h的降雨发生频率相对较低,占14.7%(图2)。

研究期间的次降雨平均强度为2.74 mm/h,最小值为0.38 mm/h,最大值为11.5 mm/h,变异系数为93.0%。降雨强度集中在0—2 mm/h,占55.9%；强度在2—5 mm/h的发生频率为32.4%；而强度>5 mm/h的发生频率较小,仅占11.8%(图2)。

2.2 林下穿透雨及其变异性

观测期间,林内穿透雨量共为483.5 mm,占同期林外降雨量的85.3%；平均单场穿透雨量14.2 mm,变异系数为118.6%。次降雨的穿透雨率大小受降雨特征明显影响,由图3可知,当次降雨量变化在0—20 mm时,穿透雨率随降雨量增加呈明显增加；当次降雨量大于20 mm时,穿透雨率渐趋稳定值(95%)。对次降雨穿透雨率和次降雨量的关系进行拟合,两者呈显著的指数函数(Exponential rise to maximum)关系,拟合效果(R2)达84.5%：

Tf(%)=98.541(1-0.894Rf)R2=0.845,n=34

式中,Tf代表林内40个测点的次降雨平均穿透雨率(%),Rf代表林外次降雨量(mm)。

林内不同测点间穿透雨的变异系数与降雨量存在显著负相关(P<0.05),由图3可知,当次降雨量<2 mm 时,穿透雨的变异系数为100%；而后,随降雨量增加而急剧下降,在次降雨量>20 mm时,基本趋于稳定值(15%左右)。穿透雨的变异系数与次降雨量的关系可用指数函数(Exponential Decay)表示,拟合度达84.8%：

CV(%)=109.962e-0.239Rf+15.342e-0.001RfR2=0.848,n=34

式中,CV代表同一场降雨林内不同测点间的穿透雨变异系数(%),Rf代表林外降雨量(mm)。

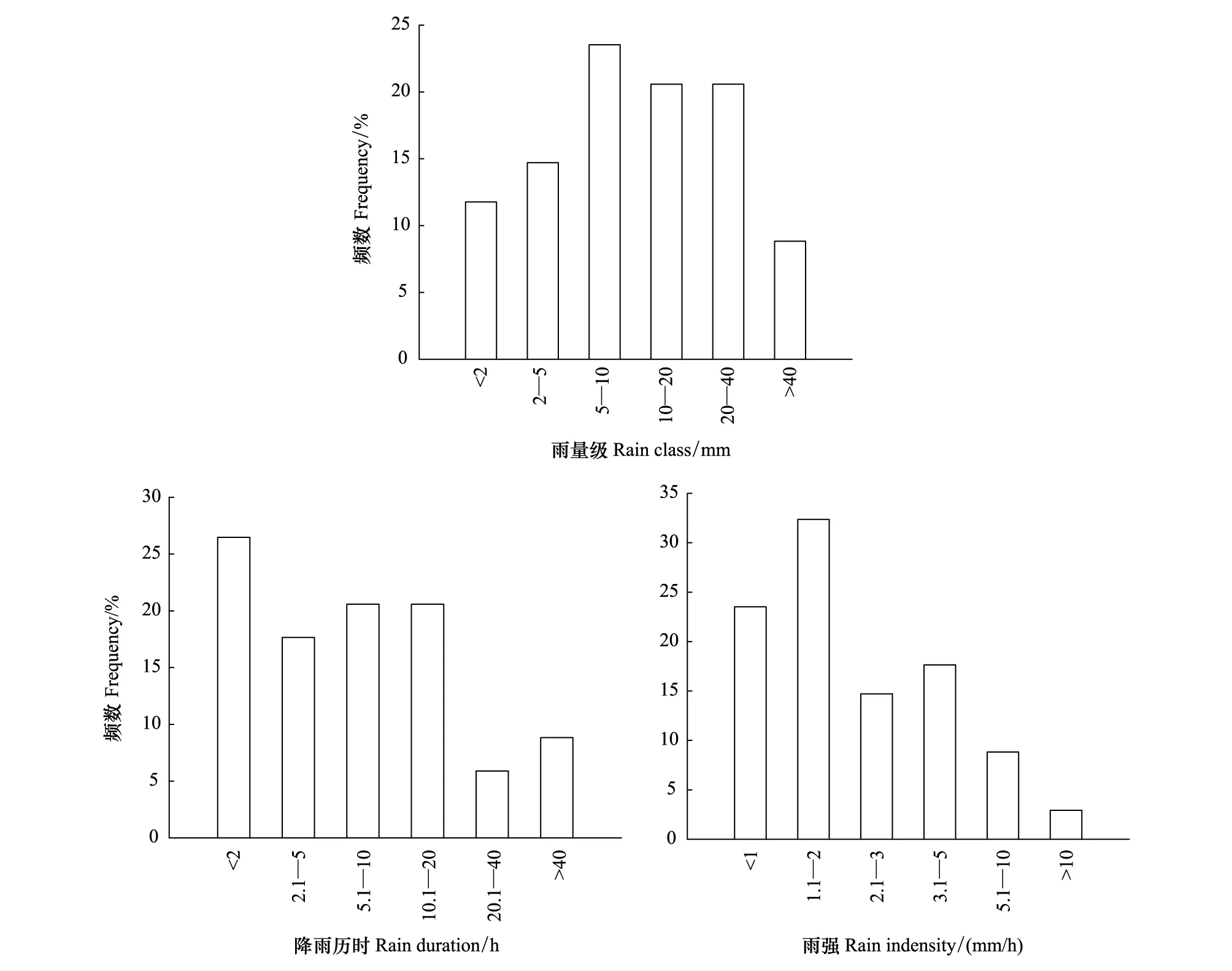
图2 研究期间的降雨特征Fig.2 Characteristics of gross rainfall during the study period

图3 研究样地的次降雨穿透雨率和穿透雨变异系数随次降雨量的变化Fig.3 Variation of the plot throughfall ratio and its CV with the depth of individual rainfall events

2.3 次降雨的穿透雨空间变异及影响因素

树木特征是影响穿透雨空间变异的重要因素,本研究考虑了测点离树干距离、测点上方冠层厚度和叶面积指数3个树木特征因子,相关性分析显示,冠层厚度与测点距树干距离存在显著的负相关(P<0.01),其他因子之间相关性不显著(表2)。图4展示了所有40个测点的穿透雨量34场降雨平均值随测点离树干距离、测点上方冠层厚度和叶面积指数的变化。可知,测点穿透雨量与测点离树干的距离呈显著正相关(P<0.05),与测点上方冠层厚度(P<0.05)和叶面积指数(P<0.05)呈显著负相关。其中,冠层厚度对穿透雨空间变异的影响最大(r=-0.379)。

图5展示了3个降雨量级条件下各测点平均穿透雨量随测点上方的叶面积指数、冠层厚度及测点离树干距离的变化。可知,穿透雨量随降雨量增大而增加,且3个林木生长指标的影响也存在一定的降雨量级差异。Pearson相关分析显示(表3),当次降雨量小于10 mm时,测点穿透雨量与测点上方叶面积指数呈显著负相关(P<0.01),与测点距树干的距离和测点上方冠层厚度不相关；当降雨量在10—20 mm时,测点穿透雨量与测点距树干的距离呈显著正相关(P<0.01),与测点上方冠层厚度呈显著负相关(P<0.01),但与测点上方叶面积指数不相关；当降雨量大于20 mm时,测点穿透雨量与3个生长指标均不显著相关。

表2 树木特征因子之间的相关性

**表示相关性在0.01水平上极显著

表3 不同雨量级下各测点穿透雨量与其上方叶面积指数、冠层厚度和距树干距离的相关性

Table 3 Correlations between throughfall of each collector and the leaf area index, canopy thickness and the distance to the nearest stem under different rainfall ranges

降雨量级Rainfallranges/mm叶面积指数Leafareaindex/(m2/m2)测点距树干的距离Distancetotheneareststem/m冠层厚度Canopythickness/m0—10-0.424**0.310-0.26210—20-0.2660.436**-0.441**>20-0.2440.222-0.300

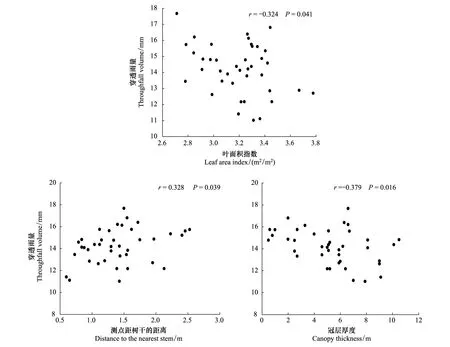
图4 所有测点平均穿透雨量随叶面积指数、冠层厚度和离树干距离的变化Fig.4 Variation of the mean throughfall of each collector with the above leaf area index, canopy thickness and the distance to nearest stem

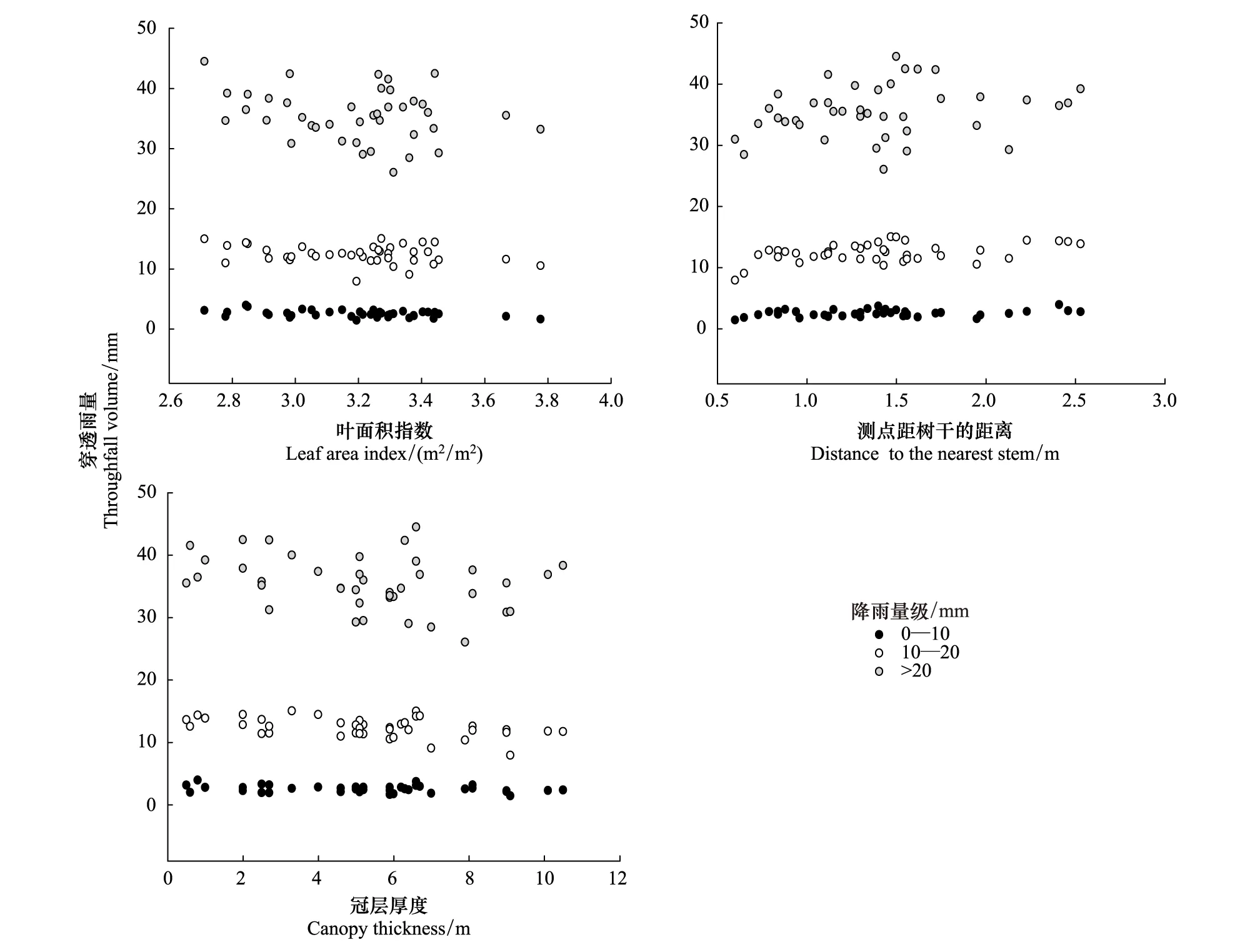
图5 不同雨量级下各测点穿透雨量随其上方叶面积指数、冠层厚度和离树干距离的变化Fig.5 Variation of throughfall of each collector with leaf area index, canopy thickness and the distance to nearest stem under different rainfall ranges

2.4 穿透雨取样器的合理数量

由图6可看出,在3个降雨量级下,随穿透雨收集器数量(n=2—39)增多,穿透雨的平均值及置信区间(CI,90%和95%)均逐渐向内收缩。

利用统计学原理,以5%和10%误差为界,分别确定在90%和95%置信区间下3个降雨量级的穿透雨收集器布设数量。在降雨量级为0—10 mm时,在95%的置信区间下,收集器数量≥13个和≥26个时,所测穿透雨值不会超过10%和5%的误差水平；在90%的置信区间下,收集器数量≥9和≥23个时,所测穿透雨值不会超过10%和5%的误差水平。在降雨量级为10—20 mm时,在95%的置信区间下,当收集器数量≥6个和≥15个时,所测穿透雨值不会超过10%和5%的误差水平；在90%的置信区间下,当收集器数量≥4和≥12个时,所测穿透雨值不会超过10%和5%的误差水平。在降雨量级>20 mm时,在95%的置信区间下,收集器数量≥5个和≥15个时,所测穿透雨值不会超过10%和5%的误差水平；在90%的置信区间下,收集器数量≥4和≥12个时,所测穿透雨值不会超过10%和5%的误差水平。

在3个降雨量级下的穿透雨平均值置信区间的上限和下限随收集器数量的变化曲线的拟合函数见表4。其中,y代表穿透雨平均值置信区间的上限或下限,x代表穿透雨收集器的数量(x<40)。可藉此直接求出在一定误差范围下所需要的穿透雨收集器数量。

图6 Monte Carlo模拟的穿透雨平均值和置信区间随雨量收集器数量的变化Fig.6 Variation of the average and confidence intervals of throughfall with collector number based on the Monte Carlo re-sampling5%、10%误差水平指占40个收集器测穿透雨量平均值的5%、10%

Table 4 The relations of the upper and lower limits of confidence describing the variation of mean throughfall with increasing collector number under 3 throughfall ranges

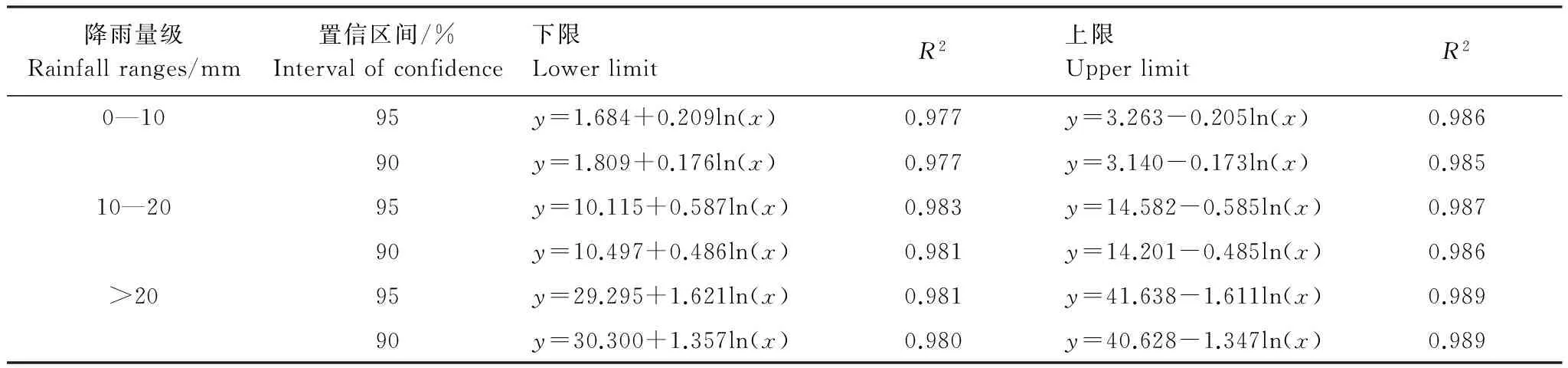
降雨量级Rainfallranges/mm置信区间/%Intervalofconfidence下限LowerlimitR2上限UpperlimitR20—1095y=1.684+0.209ln(x)0.977y=3.263-0.205ln(x)0.98690y=1.809+0.176ln(x)0.977y=3.140-0.173ln(x)0.98510—2095y=10.115+0.587ln(x)0.983y=14.582-0.585ln(x)0.98790y=10.497+0.486ln(x)0.981y=14.201-0.485ln(x)0.986>2095y=29.295+1.621ln(x)0.981y=41.638-1.611ln(x)0.98990y=30.300+1.357ln(x)0.980y=40.628-1.347ln(x)0.989

3 讨论

盛后财等[22]研究发现,兴安落叶松(Larixgmelinii)的次降雨事件的穿透雨率随降雨量增加先显著增加后渐趋稳定,本研究也得到了类似结果,当次降雨量小于20 mm时,华北落叶松林穿透雨率随降雨量增加而先快速增大后缓慢增大,当降雨量大于20 mm后不再明显增加并渐趋稳定。这是因雨量超过林冠层最大截留能力时,林冠达到饱和,降雨除了雨中蒸发和干流外全部转化为穿透雨,所以次降雨事件的穿透雨率大小很大程度上主要取决于降雨量大小[5]。随着次降雨量增大,降雨会更多地通过枝条汇入树干,以一定的比例通过干流形式进入地表,这是在次降雨量很大时穿透雨率维持在一个低于100%(100-干流率)数值的原因。

在本研究期间(2015年5月6日至10月31日),六盘山的华北落叶松林总穿透雨量为483.5 mm,占同期林外降雨量的85.3%,明显高于在祁连山测定的青海云杉(Piceacrassifolia)林的75.8%[5]、在大兴安岭测定的樟子松(Pinussylvestrisvar.mongolica)林的73.58%[23]和在大兴安岭测定的兴安落叶松林的76.57%[24],这很可能与其他研究中的研究期间内雨量级相对较小有关。

华北落叶松林内穿透雨变异系数随降雨量增加而减小,在降雨量大于20 mm后基本趋于稳定,这与其他树种的研究结果一致[1,25- 26],主要是因随降雨量增加,冠层结构特征(如郁闭度、叶面积指数和冠层厚度等)对穿透雨的影响会逐渐减弱,直至最小；穿透雨的空间变化也会相应逐渐变小并趋于稳定[27]。对油松[27]、海岸松(Pinuspinaster)[28]、兴安落叶松[22]和青海云杉[5]等针叶林的研究发现,穿透雨变异系数基本稳定在18%—22%之间,本研究中基本稳定在15%左右,低于上述研究,但与Fan等[10]研究的杂交松(Pinuselliottii×Pinuscaribaeavar.hondurensis)林的结果相当(穿透雨变异系数16.5%)。当穿透雨变异系数趋于稳定时,变异系数大小主要取决于林冠结构的空间异质性和穿透雨收集器的面积[26,29]。已有研究表明[29],穿透雨变异系数随使用的穿透雨收集器面积增大而减小。本研究和Fan等[10]使用的穿透雨收集器面积(230.58 cm2和117 cm2)均小于上述其他研究(314.2 cm2和706.5 cm2),因此,穿透雨收集器面积不是导致本研究穿透雨变异系数较小的主要原因。本研究和Fan等[10]的研究对象均为单株规则排列的人工林,林冠的空间异质性相对较低,这可能是导致本研究中穿透雨变异系数低于其他研究结果的主要原因。

已有研究表明[5,14,30],冠层结构是影响林内穿透雨空间分异的重要因素,但由于不同树种的分枝角度和叶片形态等的差异,导致影响不同树种穿透雨率的主导树木特征因子有所不同。如盛后财等[22]研究发现,兴安落叶松林的穿透雨空间分布特征主要受冠层厚度的影响；李振新等[30]研究发现,测点距主树干的距离对岷江冷杉(Abiesfaxoniana)林内穿透雨率的影响最大；而时忠杰等[14]发现,叶面积指数是影响六盘山华山松(Pinusarmandii)林内穿透雨率的主要树木特征。本研究分析了华北落叶松林内各测点的2015年生长季内34次降雨的平均穿透雨量与雨量收集器上方的叶面积指数、冠层厚度及距最近树干的距离的关系,认为这3个林木特征均是影响穿透雨空间分布的重要因素,且冠层厚度的影响最大；进一步分析发现,这些树木特征对穿透雨空间分布的影响具有降雨量级差异,当降雨量小于10 mm时,叶面积指数是主要影响因子；当降雨量变化在10—20 mm时,主要影响因子是测点距最近树干的距离及冠层厚度；当降雨量大于20 mm时,3个树木特征的影响均不显著,这类似于田风霞等[5]在祁连山研究青海云杉林内穿透雨空间分布影响因子的结论。这表明,结合降雨特征分析树木特征对林内穿透雨空间分布的影响将更加有效。

由于林下穿透雨有明显的空间异质性,为确保评估的准确性,往往需布设大量穿透雨收集器,有可能因过度大量观测而增加研究成本和时间耗费,有必要确定一定误差下的最少穿透雨收集器数量。已有研究表明[31],不同森林类型所需的最少收集器数量存在明显不同。Rodrigo等[11]利用Monte Carlo模拟重抽样方法得出的冬青栎(Quercusilex)林在95%置信区间下要满足5%的误差要求时需22个以上的收集器,在满足10%的误差要求时则需9个以上的收集器；Shen等[25]利用模拟重抽样的方法研究了栲树(Castanopsisfargesii)林穿透雨的空间分布,认为在95%的置信区间下,收集器数量大于5和10个时,所测穿透雨量值不会超过10%和5%的误差水平。本研究得出,当降雨量级在0—10 mm时,在95%的置信区间下,华北落叶松林内布设13和26个以上的穿透雨收集器时,所测穿透雨值能控制在10%和5%的误差范围内；在90%的置信区间下,布设9和23个以上的收集器能使误差控制在10%和5%以内。当降雨量级在10—20 mm时,在95%的置信区间下,华北落叶松林内布设6和15个以上的收集器时,所测穿透雨值能控制在10%和5%的误差范围内；在90%的置信区间下,布设4和12个以上的收集器能使误差不超过10%和5%的水平。当降雨量级大于20 mm时,在95%的置信区间下,华北落叶松林内布设5和15个以上收集器时,所测穿透雨量误差能控制在10%和5%内；在90%的置信区间下,布设4和12个以上的收集器能使误差不超过10%和5%。这表明,除林分类型影响穿透雨收集器布设数量外,降雨量级的影响也很大,需予以考虑。在本研究地点,由于次降雨量集中在0—10 mm,故应更多参考降雨量级0—10 mm时所需的穿透雨收集器布设数量。本研究确定的穿透雨收集器最少数量是在特定林分结构和收集器截面面积(230.58 cm2)及空间分布格局情况下的结果。如果采用的穿透雨收集器截面面积增大,会因承接更多面积来源的穿透雨而降低空间变异性[11],从而可在满足相同误差要求下采用较少的收集器。因此,要得到一个确定穿透雨收集器最低数量的通用方法,还需很多研究,如确定穿透雨收集器最低数量与收集器截面面积、森林冠层结构及空间分布格局、穿透雨收集器的空间布设格局等的数量关系。

4 结论

根据本文华北落叶松林穿透雨空间分异特征的研究,得到如下结论：

(1)随次降雨量增加,林下穿透雨率先显著增加后渐趋稳定,穿透雨的变异系数则先显著降低后趋于稳定,两者与次降雨量的关系均可用指数函数表示。

(2)各树木特征(叶面积指数、冠层厚度和测点离最近树干距离)对林下穿透雨空间分布的影响随次降雨量大小而变。叶面积指数对穿透雨空间分布的影响随次降雨量的增加逐渐减弱,而测点离最近树干距离和冠层厚度对穿透雨空间分布的影响随次降雨量的增加先增强后减弱。

(3)对本研究特定林分,考虑到次降雨量集中在0—10 mm,在95%的置信区间下,若要将穿透雨测定值控制在10%和5%误差范围内,应均匀布设13和26个以上的收集器；在90%置信区间下,控制穿透雨误差不超过10%和5%时需至少布设9和23个收集器。

[1] Shinohara Y, Onozawa Y, Chiwa M, Kume T, Komatsu H, Otsuki K. Spatial variations in throughfall in a Moso bamboo forest: sampling design for the estimates of stand-scale throughfall. Hydrological Processes, 2010, 24(3): 253- 259.

[2] Gómez J A, Vanderlinden K, Giráldez J V, Fereres E. Rainfall concentration under olive trees. Agricultural Water Management, 2002, 55(1): 53- 70.

[3] Nanko K, Onda Y, Ito A, Moriwaki H. Spatial variability of throughfall under a single tree: experimental study of rainfall amount, raindrops, and kinetic energy. Agricultural and Forest Meteorology, 2011, 151(9): 1173- 1182.

[4] 孙忠林, 王传宽, 王兴昌, 张全智. 两种温带落叶阔叶林降雨再分配格局及其影响因子. 生态学报, 2014, 34(14): 3978- 3986.

[5] 田风霞, 赵传燕, 冯兆东, 彭守璋, 彭焕华. 祁连山青海云杉林冠生态水文效应及其影响因素. 生态学报, 2012, 32(4): 1066- 1076.

[6] 田野宏, 满秀玲, 刘茜, 李奕. 大兴安岭北部白桦次生林降雨再分配特征研究. 水土保持学报, 2014, 28(3): 109- 113.

[7] 陈书军, 陈存根, 曹田健, 侯琳, 李荣华, 张硕新. 降雨特征及小气候对秦岭油松林降雨再分配的影响. 水科学进展, 2013, 24(4): 513- 521.

[8] Wullaert H, Pohlert T, Boy J, Valarezo C, Wilcke W. Spatial throughfall heterogeneity in a montane rain forest in Ecuador: extent, temporal stability and drivers. Journal of Hydrology, 2009, 377(1/2): 71- 79.

[9] Shachnovich Y, Berliner P R, Bar P. Rainfall interception and spatial distribution of throughfall in a pine forest planted in an arid zone. Journal of Hydrology, 2008, 349(1/2): 168- 177.

[10] Fan J L, Oestergaard K T, Guyot A, Jensen D G, Lockington D A. Spatial variability of throughfall and stemflow in an exotic pine plantation of subtropical coastal Australia. Hydrological Processes, 2015, 29(5): 793- 804.

[11] Rodrigo A,vila A. Influence of sampling size in the estimation of mean throughfall in two Mediterranean holm oak forests. Journal of Hydrology, 2001, 243(3/4): 216- 227.

[12] Sinun W, Meng W W, Douglas I, Spencer T. Throughfall, stemflow, overland flow and throughflow in the Ulu Segama rain forest, Sabah, Malaysia. Philosophical Transactions of the Royal Society B: Biological Sciences, 1992, 335(1275): 389- 395.

[13] 曹云, 黄志刚, 郑华, 欧阳志云. 柑桔园林下穿透雨的分布特征. 水科学进展, 2007, 18(6): 853- 857.

[14] 时忠杰, 王彦辉, 徐丽宏, 熊伟, 于澎涛, 郭浩. 六盘山华山松(Pinusarmandii)林降雨再分配及其空间变异特征. 生态学报, 2009, 29(1): 76- 85.

[15] 王卫军, 赵婵璞, 姜鹏, 任仙, 王骄洋, 王桂真, 牟雪, 谷建才. 塞罕坝华北落叶松人工林水源涵养功能研究. 中南林业科技大学学报, 2013, 33(2): 66- 68, 72- 72.

[16] 陈波, 孟成生, 赵耀新, 杨新兵, 赵心苗, 张丽峰. 冀北山地不同海拔华北落叶松人工林枯落物和土壤水文效应. 水土保持学报, 2012, 26(3): 216- 221.

[17] 刘建立, 王彦辉, 于澎涛, 程丽莉, 熊伟, 徐丽宏, 张淑兰, 杜阿朋. 六盘山叠叠沟小流域华北落叶松人工林的冠层降水再分配特征. 水土保持学报, 2009, 23(4): 76- 81.

[18] 段旭, 王彦辉, 于澎涛, 熊伟, 徐丽宏. 六盘山分水岭沟典型森林植被对大气降雨的再分配规律及其影响因子. 水土保持学报, 2010, 24(5): 120- 125.

[19] 徐丽宏, 时忠杰, 王彦辉, 熊伟, 于澎涛. 六盘山主要植被类型冠层截留特征. 应用生态学报, 2010, 21(10): 2487- 2493.

[20] 时忠杰, 王彦辉, 熊伟, 于澎涛, 郭浩, 张雷燕, 董晓红. 单株华北落叶松树冠穿透降雨的空间异质性. 生态学报, 2006, 26(9): 2877- 2886.

[21] 熊伟, 王彦辉, 于澎涛, 刘海龙, 时忠杰, 管伟. 六盘山南坡华北落叶松(Larixprincipis-rupprechtii)树干直径生长及其对气象因子的响应. 生态学报, 2007, 27(2): 432- 441.

[22] 盛后财, 蔡体久, 俞正祥. 大兴安岭北部兴安落叶松(Larixgmelinii)林下穿透雨空间分布特征. 生态学报, 2016, 36(19)：6266-6273..

[23] 李奕, 蔡体久, 满秀玲, 田野宏. 大兴安岭地区天然樟子松林降雨截留再分配特征. 水土保持学报, 2014, 28(2): 40- 44.

[24] 盛后财, 蔡体久, 李奕, 刘玉杰. 大兴安岭北部兴安落叶松林降雨截留再分配特征. 水土保持学报, 2014, 28(6): 101- 105.

[25] Shen H T, Wang X X, Jiang Y, You W H. Spatial variations of throughfall through secondary succession of evergreen broad-leaved forests in eastern China. Hydrological Processes, 2012, 26(11): 1739- 1747.

[26] Staelens J, De Schrijver A, Verheyen K, Verhoest N E C. Spatial variability and temporal stability of throughfall water under a dominant beech (FagussylvaticaL.) tree in relationship to canopy cover. Journal of Hydrology, 2006, 330(3/4): 651- 662.

[27] 战伟庆, 张志强, 武军, 肖金强. 华北油松人工林冠层穿透雨空间变异性研究. 中国水土保持科学, 2006, 4(3): 26- 30, 35- 35.

[28] Loustau D, Berbigier P, Granier A, Moussa F E H. Interception loss, throughfall and stemflow in a maritime pine stand. I. Variability of throughfall and stemflow beneath the pine canopy. Journal of Hydrology, 1992, 138(3/4): 449- 467.

[29] Zuecco G, Oliviero O, Penna D, van Meerveld I, Hopp L, Dalla Fontana G, Borga M. Spatial and temporal variability of throughfall at the plot scale in the Italian pre-Alps//Proceedings of EGU General Assembly 2014. Vienna, Austria: NASA, 2014: 12563.

[30] 李振新, 郑华, 欧阳志云, 王效科, 刘兴良, 宿以明. 岷江冷杉针叶林下穿透雨空间分布特征. 生态学报, 2004, 24(5): 1015- 1021.

[31] Kimmins J P. Some statistical aspects of sampling throughfall precipitation in nutrient cycling studies in British Columbian Coastal Forests. Ecology, 1973, 54(5): 1008- 1019.

Spatial variations of throughfall in aLarixprincipis-ruprechtiiplantation of Liupan Mountains, Ningxia, China

LIU Zebin1,WANG Yanhui1,*,DENG Xiuxiu2,LIU Yu3,ZHANG Tong3,ZUO Haijun1,WANG Yarui1,XIONG Wei1,YU Pengtao1,XU Lihong1

1KeyLaboratoryofForestEcologyandEnvironment,StateForestryAdministration;ResearchInstituteofForestEcology,EnvironmentandProtection,ChineseAcademyofForestry,Beijing100091,China2CollegeofForest,CentralsouthUniversityofForestryandTechnology,Changsha410004,China3CollegeofSoilandWaterConservation,BeijingForestryUniversity,Beijing100083,China

The depth and spatial distribution of throughfall under the forest canopy can affect the hydrological (i.e., infiltration, runoff and evaporation) and ecological processes (i.e., tree growth, litter decomposition) of forest ecosystems. Therefore, both the evaluation of forest hydrological impacts and forest ecosystems management require an accurate description of the spatial distribution of throughfall. In order to interpret the spatial heterogeneity of throughfall in the plantation ofLarixprincipis-ruprechtii, a 30 m × 30 m sized stand plot was set up in the Xiangshuihe watershed of the Liupan Mountains. Within this plot, 40 throughfall collectors, with a size of 230.58 cm2, were evenly installed. The throughfall depth of 34 rainfall events was measured individually during the growth season (May—Oct.) of 2015. The gross rainfall in open field in the study period was 567.0 mm, and the throughfall depth in the plantation plot was 483.5 mm, accounting for 85.3% of gross rainfall. As rainfall increased, the throughfall ratio first increased and then tended to stabilize. A considerable spatial variation of throughfall was observed, and the coefficient of variance of throughfall first decreased and then became constant with increase in rainfall. The spatial distribution of throughfall was influenced by the tree characteristics canopy leaf area index and canopy thickness above throughfall collector, and the distance from throughfall collector to the nearest stem, and this influence varied with the depth of rainfall. When the rainfall was less than 10 mm, throughfall showed a significantly negative correlation with the leaf area index; when the rainfall varied within the range of 10—20 mm, throughfall showed a significant positive correlation with the distance to the nearest stem and a significantly negative correlation with canopy thickness. However, when the rainfall was more than 20 mm, throughfall showed no correlation with any of the tree characteristics. Considering that the depth of individual rainfall events is concentrated within 0—10 mm, at least 13 or 9 throughfall collectors with the size used here are required for a plot of 30 m×30 m if the error of measured throughfall should be controlled within 10% under confidence levels of 95% or 90%. At least 26 or 23 throughfall collectors are required when the error should be controlled within 5% under confidence levels of 95% or 90%.

Larixprincipis-ruprechtii；throughfall；spatial variation；Monte Carlo simulation

国家自然科学基金项目(41390461,41230852,41471029)

2016- 02- 21; 网络出版日期:2017- 02- 17

10.5846/stxb201602210305

*通讯作者Corresponding author.E-mail: wangyh@caf.ac.cn

刘泽彬,王彦辉,邓秀秀,刘宇,张桐,左海军,王亚蕊,熊伟,于澎涛,徐丽宏.六盘山华北落叶松林下穿透雨空间变异特征.生态学报,2017,37(10):3471- 3481.

Liu Z B,Wang Y H,Deng X X,Liu Y,Zhang T,Zuo H J,Wang Y R,Xiong W,Yu P T,Xu L H.Spatial variations of throughfall in aLarixprincipis-ruprechtiiplantation of Liupan Mountains, Ningxia, China.Acta Ecologica Sinica,2017,37(10):3471- 3481.