钢材弹塑性分析的新模型
2017-06-22柯江
柯 江
(陕西理工大学土建学院,陕西 汉中 723001)
钢材弹塑性分析的新模型
柯 江
(陕西理工大学土建学院,陕西 汉中 723001)
基于正六面体微元与桁架单元的受力变形等效,建立了一个桁架单元新模型,求解了钢材的弹塑性平面应力问题和空间问题,并通过大量的计算实例,验证了该新单元模型具有良好的计算精度。
桁架单元,钢材,弹塑性,平面应力
钢材是一种塑性材料,目前按照传统理论的多轴屈服准则、多轴弹塑性本构关系模型,进行弹塑性分析非常复杂。基于受力变形等效,笔者提出了一个由多个杆件组成的桁架单元新模型,采用新模型计算线弹性材料,后来推广到理想弹塑性材料(存在缺陷:适用范围小,并且杆件受压屈服后无法传递更大荷载)、一般弹塑性材料[1-5],本文将提出一种具有普遍适用性的钢材(同样适用于其他塑性材料)弹塑性分析新模型,文献[4][5]中塑性材料的新模型只是本文的两种特殊情况,最后给出应用实例来验证。
1 桁架单元新模型
基于正六面体微元与桁架单元的受力变形等效,建立桁架单元的新模型。新单元模型包括空间桁架单元(如图1所示,适用于空间问题)与平面桁架单元(如图2所示,适用于平面应力问题)。材料的泊松比v:空间问题取v=0.25,平面应力问题取v=
1/3。E为弹性模量,σ0为材料的拉伸(或压缩)屈服应力,τ0为材料的纯剪切屈服应力。εa,εu分别为材料单轴受压应力应变曲线的水平屈服段的末点应变、极限压应变;εb,εc为两个中间控制点的竖向压应变;γ0为材料的纯剪切屈服应力所对应的剪应变。
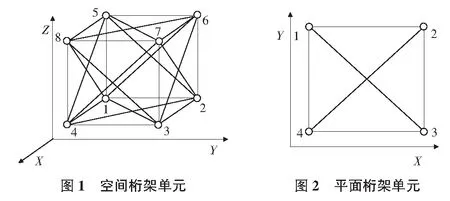
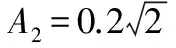

表1 平面应力问题不同n值时所对应的参数值

表2 空间问题不同n值时所对应的参数值
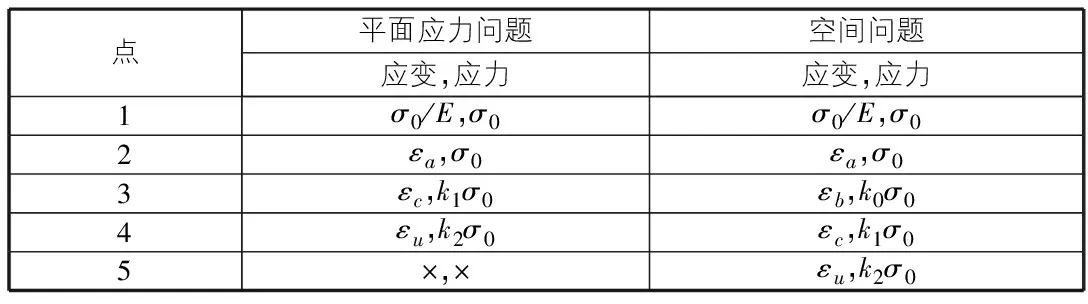
表3 材料单轴受压

表4 材料单轴受拉
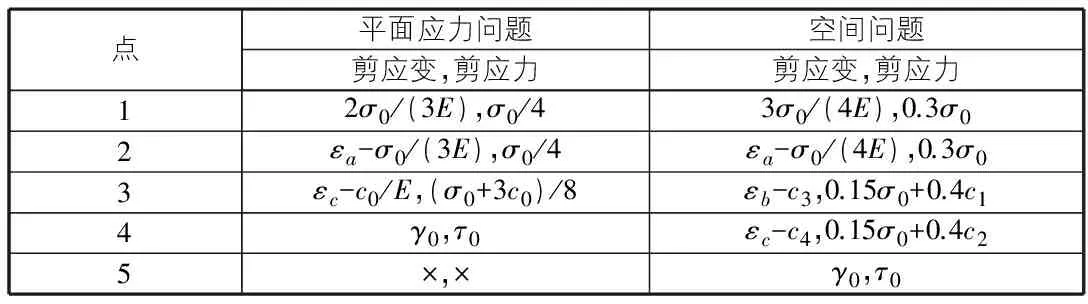
表5 材料受剪

表6 平行杆受压

表7 平行杆受拉

表8 斜杆受压

表9 斜杆受拉

表10 平面应力问题不同n值时k1的建议值

表11 空间问题不同n值时k0,k1的建议值
2 应用实例
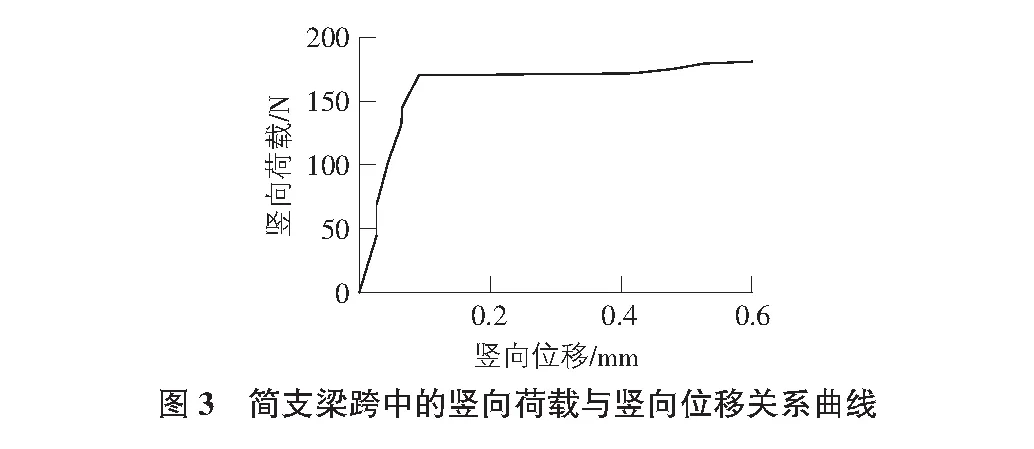
一简支钢梁,跨度28 mm,截面高度4 mm、宽度1 mm,弹性模量E=200 000 N/mm2,泊松比v=1/3,屈服应力σ0=300 N/mm2,n=τ0/σ0=0.5,εa=0.05,εc=0.101 5,εu=0.5,γ0=0.1,在跨中施加竖直向下的位移荷载求所能承受的极限荷载,按平面应力问题所对应的平面桁架单元新模型来计算,单元尺寸均为1 mm×1 mm,一共划分为112个新单元,平行杆截面面积为0.375 mm2,斜杆截面面积为0.530 33 mm2,桁架单元中平行杆、斜杆的应力应变曲线按表6~表9取值,其中,k1=3,k2=50,c0=300 N/mm2。采用有限元软件计算可得跨中的竖向荷载与竖向位移关系曲线(见图3),该曲线水平段所对应的荷载为171.429 N,而按照理想弹塑性模型的塑性力学理论解为171.429 N,两者完全吻合。
3 结语
目前,钢材的弹塑性分析涉及多轴本构关系、多轴屈服准则,不管是理论计算还是数值计算都非常复杂,本文提出的桁架单元新模型,计算时只需要输入单轴受压、受拉应力应变曲线,因此计算很简单,经过大量对比计算,可以发现新单元模型的计算精度良好。
[1] 王 仁,黄文彬,黄筑平.塑性力学引论[M].北京:北京大学出版社,1992.
[2] 柯 江.实体结构求解的新方法[J].山西建筑,2008,34(9):112-113.
[3] Ke Jiang.A New Element Model of Solid Bodies[J].Applied Mechanics and Materials,2012(174-177):2115-2118.
[4] 柯 江.基于固体新单元模型分析理想弹塑性问题[J].山西建筑,2012,38(36):42-43.
[5] 柯 江.弹塑性固体的新单元模型[J].山西建筑,2016,42(31):46-47.
A new model for elasto-plastic analysis of steel
Ke Jiang
(SchoolofCivilEngineeringandArchitecture,ShaanxiUniversityofTechnology,Hanzhong723001,China)
Based on stress deformation equivalent of vertical hexahedron microelement and truss element, a new truss element model is presented. It can be used to solve the elasto-plastic plane stress problem and spatial problem of steel. Through a large number of examples, the new element model can be found to have good accuracy.
truss element, steel, elasto-plastic, plane stress
1009-6825(2017)14-0023-03
2017-03-09
柯 江(1976- ),男,硕士,讲师
TU311.41
A
