通信塔架再分节段斜杆面外计算长度系数的研究

梅 雨

(同济大学，上海 200092)



通信塔架再分节段斜杆面外计算长度系数的研究

梅 雨

(同济大学，上海 200092)

对通信塔架再分式“K字型”节段的斜杆在塔身平面外的计算长度系数进行了参数分析，并与当前技术文件的相关规定进行了对比，最后提出了具有一定精确性和安全性的实用计算公式。

通信塔架，格构式塔，再分式节段，计算长度系数

1 概述

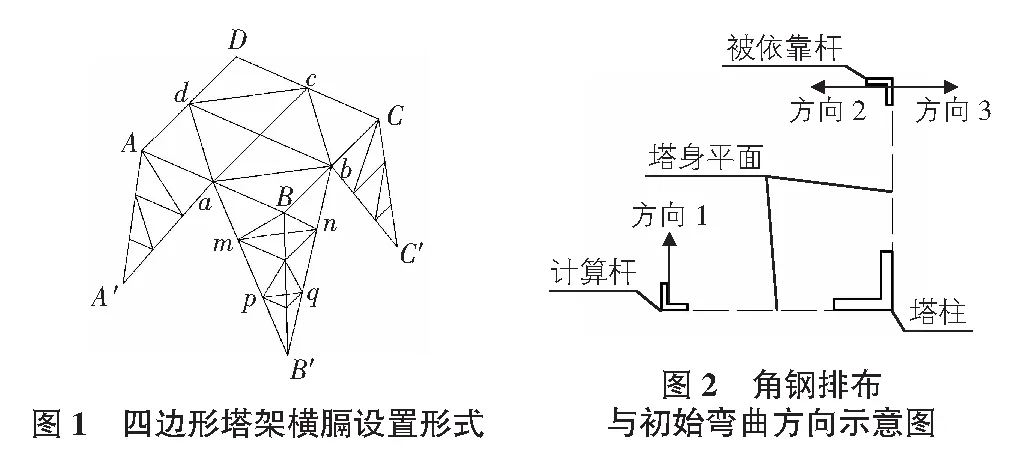
通信塔架的再分式构造常应用于塔身中下段，在塔脚处的应用尤其常见。通过设置辅助杆减小塔柱和主要受力腹杆计算长度的做法带来的经济效益是显而易见的。另一方面，通信塔架的设计逐渐趋于标准化和统一化，这使得“K字型”腹杆的应用日趋广泛。图1为一层再分式的“K字型”节段，除设置塔身平面内的辅助杆外，斜杆aB′和bB′之间设置了再分式的横膈mn及pq(下称连杆)，以减小主斜杆aB′和bB′在塔身平面外的计算长度系数。

对于aB′杆，连杆能否真正起到面外支撑的作用，取决于mn及pq杆的刚度和被依靠杆斜杆bB′提供的支承力度。连杆mn及pq通常受力很小，按《高耸结构设计规范》[1](以下简称《高耸规范》)规定的受压辅助杆长细比限值200设计，已能满足刚度和强度要求。aB′杆的计算长度系数取决于bB′杆所提供的支承力度。

现行国家标准《高耸规范》和电力行业标准《架空输电线路杆塔结构设计技术规定》[2](以下简称《杆塔规定》)对图1再分式“K字型”节段主斜杆aB′长细比的计算式规定见表1。

表1 我国现行规范和标准对再分式节段主斜杆长细比计算式的规定

文献[3]给出了斜杆aB′计算长度系数的计算式(1)，该式与《钢结构设计规范》[4]给出的交叉斜杆一杆受压一杆受拉时压杆的计算长度系数的计算式完全相同。

(1)

观察表1可知，当被依靠杆bB′受压时，《高耸规范》和《杆塔规定》的规定存在较大差别。另外，两本规范虽区分了相邻杆受压和受拉的不同情况，但忽略了两主斜杆轴力比的变化对受压主斜杆长细比的影响。式(1)给出了计算长度系数随轴力比变化的函数，但是否适用于分段数的情况，还有待求证。

本文利用有限元分析软件ANSYS建立4种分段情况的再分式“K字型”节段模型，在考虑角钢实际排布方式和初始弯曲的条件下，分析斜杆在塔身平面外的计算长度系数取值，并提出斜杆计算长度系数的实用计算公式。

2 分析模型与假定

2.1 分析模型设计

分析模型为一层“K字型”节段的一腿(如图1的abBB′部分)。分析将不考虑塔柱的受力状态对斜杆屈曲的影响，处理方法为约束塔柱等分点的水平平动自由度。分析认为斜杆在端部节点所受约束都是固定铰支，处理方法为不设置主横膈杆(如图1的ab)，同时横杆设置为二力杆，约束斜杆上端点的面外平动自由度。

2.2 分析假定

依据上节关于分析模型设计的讨论，分析引入如下假定：1)主斜杆在端节点铰接，在中间节点连续。2)辅助杆均为二力杆。3)不考虑塔身平面的倾斜。4)主斜杆角钢的肢面与塔面平行(见图2)。5)主斜杆初始弯曲方向与角钢的肢面平行，分析只考虑主斜杆在塔身平面外的初始弯曲。计算主斜杆的初始弯曲方向指向塔身内部(见图2)。6)主斜杆为大长细比构件，主斜杆在全截面屈服前已失稳。

3 有限元模型的建立

3.1 分析模型设计

模型参数包括斜杆规格、被依靠斜杆(以下简称被依靠杆)与计算斜杆(以下简称计算杆)轴力比θ、主斜杆分段数n。n考虑2～5共4种情况，均为常见的再分式分段数。每种n值对应的模型尺寸及腹杆布置方式见表2(由于不考虑腹杆布置形式的影响，各分段情况下采用最简单的腹杆布置方式)。主斜杆取6种不同规格的角钢截面：L75×5，L80×5，L90×6，L100×6，L110×7，L125×8。由表2可知各分段情况下主斜杆节间长度均为2.5 m，上述6种规格角钢对应的节间长细比分别为167，156，139，125，114，100。设计算主斜杆压力为P，被依靠主斜杆压力为P′，则θ=P′/P。规定压力符号为正，拉力符号为负。θ取值范围为[-1，1]，间隔0.1。

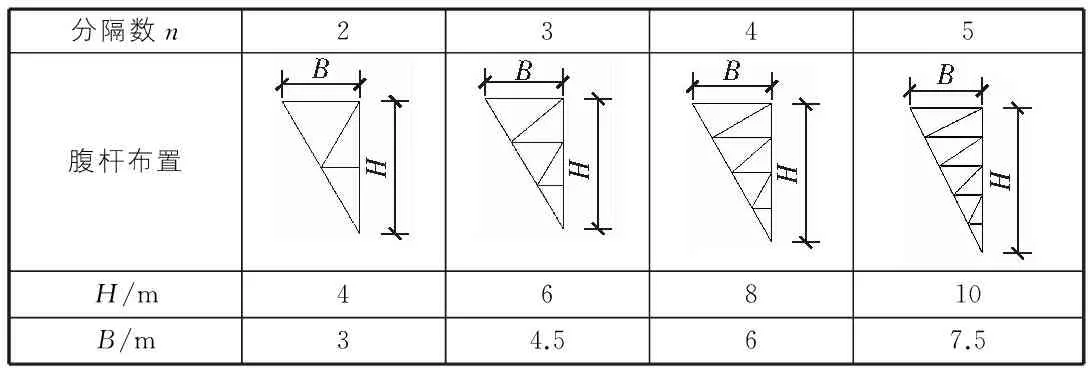
表2 各分段情况模型立面尺寸和腹杆布置

除主斜杆外，其他杆件截面均按《高耸规范》规定的长细比限值确定。所选钢材均为Q235B。由于分析不考虑塔柱的受力状态对主斜杆屈曲的影响，约束了塔柱等分点的水平平动自由度，因此无需进行塔柱截面的选材，可任取规格(本文建模选择L200×14)。

3.2 初始弯曲的规定

综合考虑主斜杆的初弯曲和荷载偏心，取主斜杆的初弯曲矢高为全长的1/500[5]。文献[6]指出计算杆和被依靠杆之间的初始弯曲存在一定的相互作用。结合2.2节分析假定，规定计算杆初始弯曲方向为图2所示方向1，被依靠杆初始弯曲方向考虑图2所示的方向2、方向3两种情况。规定被依靠杆初始弯曲方向为方向2时为情况1，被依靠杆初始弯曲方向为方向3时为情况2。

本节对主斜杆计算长度系数的研究取对计算杆不利的初始弯曲组合情况：被依靠杆受拉时(θ∈[-1,0))，按情况1施加初始弯曲；被依靠杆受压时(θ∈(0,1])，按情况2施加初始弯曲。

3.3 模型的建立与荷载的施加

采用通用有限元程序ANSYS14.5对每一确定参数的“脚”进行建模。主斜杆、塔柱采用Beam188单元模拟。Beam188单元为3D线性有限应变梁单元，适合于考虑几何大变形的弹塑性分析。其余杆件采用Link180单元模拟。Link180单元为3D有限应变杆单元，可模拟空间二力杆。计算杆和被依靠杆均约束扭转自由度。材料弹性模量E=2.06×105N/mm2。分析打开大变形开关。

荷载施加方向为计算杆和被依靠杆的轴线方向。计算杆和被依靠杆施加的轴向荷载分别为F，θF，F=A×fy，其中，A为计算杆截面面积；fy为计算杆材料的屈服强度，被依靠杆轴向力大小为θF。

4 数值计算结果与分析

4.1 数值计算结果与既有结论的对比

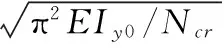
在主斜杆分别取前述6种规格角钢时，μe关于θ的变化图见图3。分析上述结果，可得出以下结论：1)随着θ的增加，在相同主斜杆规格和分段数n下，μe单调增大。2)随着主斜杆规格的增加，在相同θ值和分段数n下，μe增大。由于节间长度为定值，可认为随着计算杆节间长细比的减小，μe增大。3)随着分段数n的增加，在相同主斜杆规格和θ值下，μe逐渐减小。该结果表明，塔身平面内计算杆被支撑点的数目越多，计算杆所受塔身面内的约束作用越强，这种约束作用越有利于提高计算杆的极限承载力。造成该结果的原因与主斜杆的排列方式有关，按本文所确定的排列方式排列的角钢构件，绕弱轴弯曲时的弯曲方向并不与塔身平面垂直，面内辅助杆会抵抗计算杆的绕弱轴弯曲，对计算杆造成约束作用。4)数值计算结果与《高耸规范》《杆塔规定》的相关规定以及式(1)的结论存在一定偏差。与数值计算结果对比，被依靠杆受拉时(θ∈[-1,0))，《高耸规范》和《杆塔规定》在主斜杆规格较小(L75×5，L80×5)且被依靠杆轴拉力较大(约θ∈[-1,-0.6])时与数值计算结果较接近且略偏安全，随着主斜杆规格的增加和被依靠杆轴拉力的减小，《高耸规范》和《杆塔规定》趋于不安全。式(1)在被依靠杆轴拉力较小时与数值计算结果较接近，略不安全，随着被依靠杆轴拉力的减小，该式趋于安全。被依靠杆受压时(θ∈(0,1])，《高耸规范》偏安全，且安全系数较大。《杆塔规定》基本偏不安全。式(1)偏安全，安全系数最大。

4.2 数值计算结果拟合

为工程设计方便，根据图3的计算结果拟合出设计公式,即：

(2)

其中,θ为被依靠杆轴力与计算杆的轴力比；λc=l0/iy0，l0=L/n，L，n分别为计算杆全长和分段数；系数a，b取值如表3所示。

数值计算结果与式(2)计算结果的误差百分比见表4。

表3 系数a，b取值表

由表4可见，最大误差绝对值不超过5%。鉴于表4存在正误差，为保证安全，建议将式(2)的计算值乘以1.1的放大系数。因此，对于再分式“K字型”节段斜杆的计算长度系数的建议计算式为：

(3)

其中，系数a，b值查阅表3。

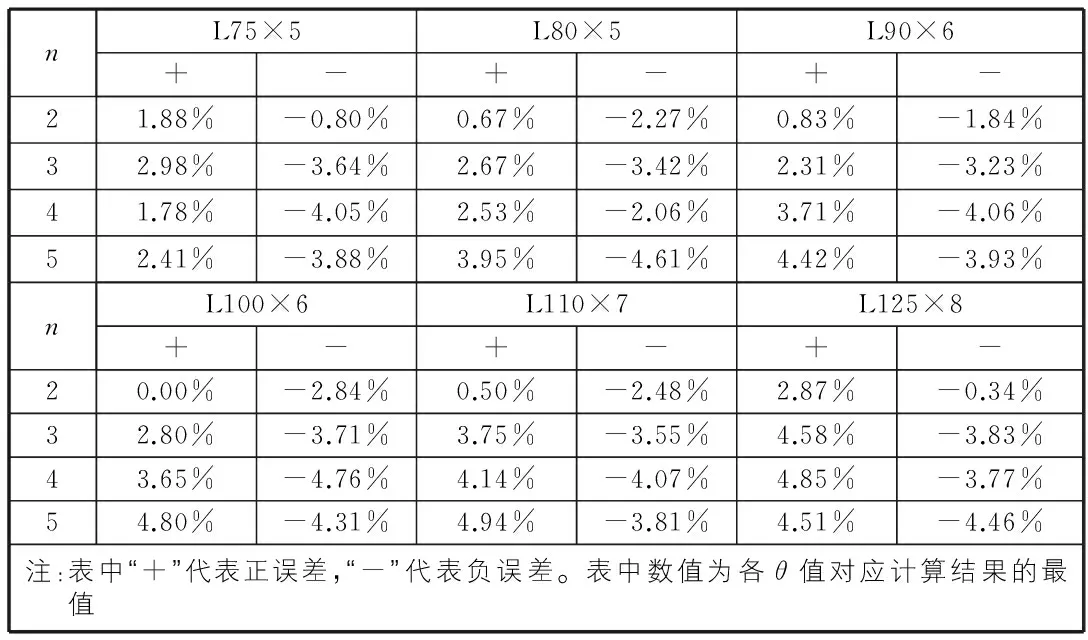
表4 数值计算结果与式(2)计算结果的误差百分比

由于角钢通信塔的再分式“K字型”节段的常见分隔数为2或3，因此可根据前述数值计算结果拟合出适用于分隔数n=2，3时的计算式：

μe=0.1[(-4n+17.5)θ2+(5.9n+1.9)θ-5.9n+42.7]1/2

(4)

其中,n=2，3。该式与数值计算结果的最大误差绝对值小于5%。

运用式(4)计算主斜杆在塔身平面外的计算长度系数时无需查表，实用性更强。考虑1.1的安全系数，可得主斜杆塔身平面外计算长度系数的实用计算式：

μe=0.11[(-4n+17.5)θ2+(5.9n+1.9)θ-5.9n+42.7]1/2

(5)

其中，n=2，3。

5 结语

通过以上分析，可得出以下结论：1)通信塔架再分节段斜杆在面外的计算长度系数μe与θ呈正相关，与n及主斜杆节间长细比呈负相关。2)现行《高耸规范》和《杆塔规定》关于“K字型”节段斜材长细比的规定在被依靠杆受压时有较大的出入。在被依靠杆受压时，与数值计算结果相比，《高耸规范》的相关规定偏安全，而《杆塔规定》的相关规定偏不安全。被依靠杆受拉时，二者结论相同，与数值计算结果相比偏不安全。式(1)计算值与数值计算结果相比，被依靠杆受拉力较大时偏不安全，其他情况偏安全且有较大余度。3)利用式(3)，式(5)计算的斜杆计算长度系数，与数值计算结果较为接近，同时具有一定的安全余度。

[1] GB 50135—2006，高耸结构设计规范[S].

[2] DL/T 5154—2012，架空输电线路杆塔结构设计技术规定[S].

[3] 陈绍蕃.钢结构设计原理[M].北京:科学出版社,2005.

[4] GB 50017—2003，钢结构设计规范[S].

[5] 童根树.柱间水平撑杆设计方法[J].西安冶金建筑学院学报，1986(3):111-140.

[6] 赵金友.竖向荷载下纵向柱列支撑的设计方法研究[D].哈尔滨：哈尔滨工业大学，2009.

[7] 王肇民，马人乐.塔式结构[M].北京：科学出版社，2004.

Research on the coefficient of lateral calculated length of diagonals in a communication tower’s subdivided segment

Mei Yu

(TongjiUniversity,Shanghai200092,China)

A parametric analysis of the coefficient of lateral calculated length of diagonals in a communication tower’s subdivided segment is conducted, as well as the comparison analysis between the numerical result and existing codes. It shows it can be more accurate and safe to calculate the coefficient of lateral calculated length of diagonals in subdivided segments with the recommended formulas.

communication tower, latticed tower, subdivided segment, coefficient of lateral calculated length

1009-6825(2016)18-0037-04

2016-04-14

梅 雨(1990- )，男，在读硕士

TU311.4

A