Sound Field Separation Technique Based on Acoustic Radiation Modes

GUO Liang,ZHU Hai-hao,MAO Rong-fu,SU Jun-bo,CHEN Zhi-min

(a.Institute of Noise&Vibration;b.National Key Laboratory on Ship Vibration&Noise; c.Collegue of Power Engineering,Naval University of Engineering,Wuhan 430033,China)

Sound Field Separation Technique Based on Acoustic Radiation Modes

GUO Lianga,b,ZHU Hai-chaoa,b,MAO Rong-fua,b,SU Jun-boa,b,CHEN Zhi-minc

(a.Institute of Noise&Vibration;b.National Key Laboratory on Ship Vibration&Noise; c.Collegue of Power Engineering,Naval University of Engineering,Wuhan 430033,China)

To eliminate the influence of the disturbing acoustic noise on reconstruction precision of near-field acoustic holography,a sound field separation technique with single hologram is proposed. In case the target source and the disturbing source are coherent,a mathematical model for the radiation of sources is set up by means of acoustic radiation mode theory.Two groups of sub-data are obtained by resampling acoustic pressures on a monolayer array and mathematical formulas are constructed between each group of sub-data and the acoustic radiation mode of sources.Then the expansion coefficients of the corresponding acoustic radiation modes can be calculated.Finally,the sound field response of the target source is reconstructed to complete sound field separation.Two numerical simulations were done to validate the proposed technique.In the first case,a simply supported plate is used as the target source and a rigid pulsating ball as the disturbing source,and in the second case,two rigid pulsating balls are used as the target and disturbing source respectively.Five parameters that would affect the validity of the proposed method were investigated in detail.Both the results show that the proposed approach is feasible and effective.

acoustic radiation modes;single layer array;sound field separation technique; near-field acoustic holography

0 Introduction

As a kind of noise source identification and location technology with high spatial resolution,near-field acoustical holography(NAH)has unparalleled technical advantages and extensive application prospects for sound visualization and sound field reconstruction[1-2].However, current NAH techniques require a free-field condition,meaning that all target sources should be located on the same side of the measurement surface and there should be no disturbing sources on the opposite side of the array.In reality,the free-field condition is not feasible in a measurement environment,which strongly influences the test accuracy and limits the application of NAH technology.

To eliminate the influence of disturbances,the sound field separation technique(FST)is necessary.Typical FST in the structural acoustic field is set up by establishing a set of primary functions which represent the radiation sound waves from both sides of the measurementsurfaces,constructing certain space transformation formulas and obtaining the complex coefficients of the primary functions in order to separate two types of different sound waves in opposite directions.Such double measurement method based on equivalent source method,spherical harmonic superposition method,statistical optimal NAH and boundary element method have been developed for years[3-8].Later,FST based on measurement of both the sound pressure and the normal component of the particle velocity is also developed for the same purpose[9-11].However,the double measurement surfaces described above should be conformal and be positioned precisely parallel to each other,which should take very much time and require more accurate layout techniques.In addition,the special pressure-particle velocity sensors,which were used to measure both the sound pressure and the normal component of the particle velocity are too expensive to be widely used.

A new method is proposed in this paper,reling on measurement of the sound pressure in a single layer based on acoustic radiation modes which are representing independent sound pressure distributions[12-15].Firstly,mathematical formalisms of the sound field are established by superposition of the acoustic field distribution modes.Secondly,the formulas for acoustic field separation are established based on these mathematical models.Thirdly,by resampling the acoustic pressures in a single array,two groups of sub-data are obtained and combined with the formulas to calculate the expansion coefficients of the corresponding acoustic radiation modes.Finally,the sound field response of the target source can be reconstructed to achieve sound field separation by multiplying the acoustic radiation modes with their expansion coefficients.

1 Theory

By letting the source structures be distributed inside the homogeneous fluid where ρ0is the mean density of the medium,ω is the angular frequency of the harmonic vibration of the surface S0enclosing the volume Vias shown in Fig.1,the sound pressure at the vector position r′in the sound field V0satisfies the Helmholtz equation in external domain, the Neumann equation at the boundary surface and the Sommerfeld equation at infinity. If the method is a valid formulation,the equations equivalent to the internal and external Helmholtz integral equation can be obtained:

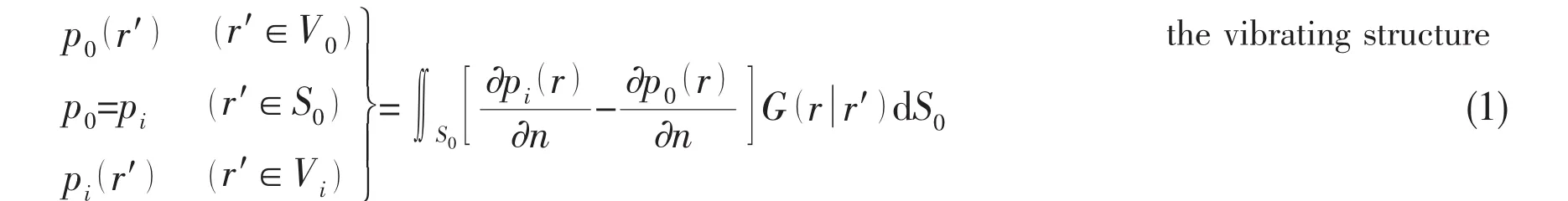
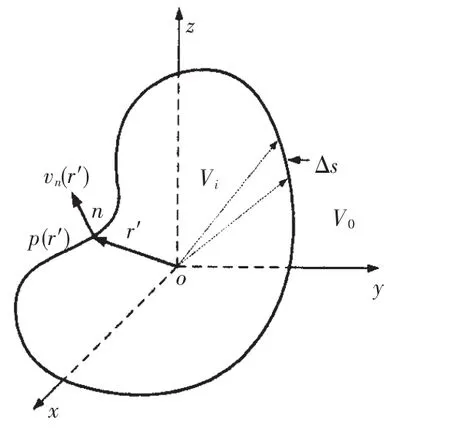
Fig.1 Schematic diagram of the vibrating structure

where k is the wave-number,c0is the familiar expression for the sound speed and μ（）ris the source strength density on the structure surface.Based on Eq.(2),the pressure can be expressed as follows:

Then,the normal velocity at vector position r′in terms of the Rayleigh integral can be obtained:

As the pressure and normal velocity are obtained,the radiated power from the source structure surface described above by a discrete number of velocity measurements can be found by the following relation in a matrix form[16].

where R represents radiation resistance which is real and symmetric.In matrix form,

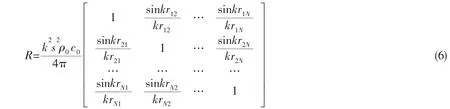
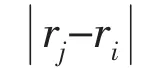
where C is a vector of expansion coefficients.Each element in C represents the contribution of the individual eigenvectors in Φ to the vector μ.Substituting Eq.(7)into Eq.(3),the pressure matrix in the field can be obtained as follows:

Generally,this will fail to reconstruct the target source directly when there are two sources on both sides of the hologram.Based on the idea of separation methods with double layer measurements,two groups of sub-data are obtained by resampling the pressure data on the hologram.As Fig.2 shows,the sub-data with the hollow tag is the first set of data,expressed as P1;and the sub-data with solid tag is the second set of data,expressed as P2,which can be considered to be the data measured with double layer measurements.

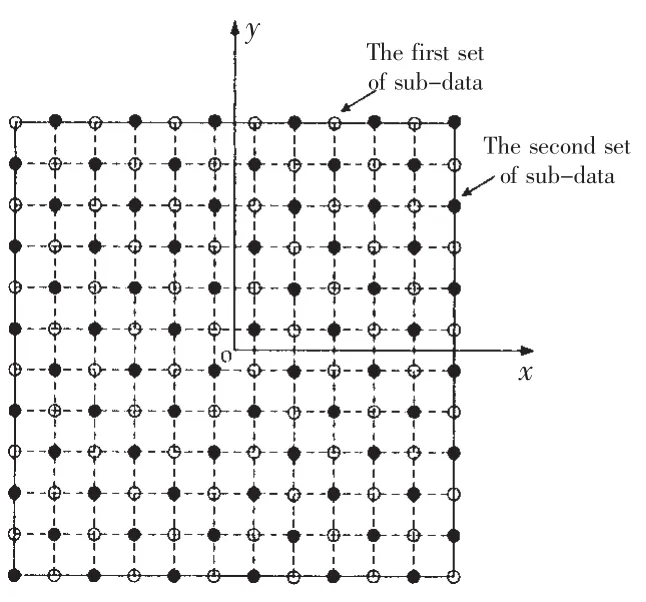
Fig.2 The data grouping after sampling

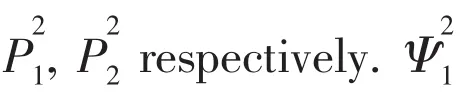
By combining Eqs.(9)and(10),we can obtain

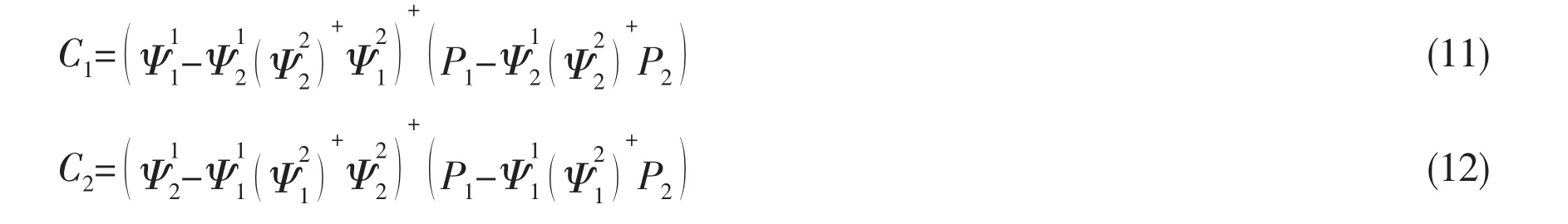
where‘+’means the pseudo inverse.Eq.(11)and Eq.(12)yield the coefficient vector C1,C2, based on which the pressure on the measurement can be obtained.When the condition numberof Ψ is larger,a regularization process is needed.In this study,Tikhonov regularization was used and the regularization parameter was chosen using L-curve method[19].By substituting the expansion coefficients C1,C2into Eq.(9),it can be obtained:

As in expansion theory,the low-order terms represent the propagating wave,while the high-order terms represent the evanescent wave.The accuracy of separation at each measurement location gives the best fit to the number of acoustic radiation modes.Since inherent illconditioning difficulty exists in the process,if more expansion terms are selected than needed, the higher-order evanescent wave error sensitivity effect will be amplified.The actual value would be masked by the error data,leading to separation failure.If less expansions terms are selected than needed,the measurement information may be incomplete,which would also cause separation failure.Therefore,it is imperative to find the optimal number Jopwhich will minimize the separation error.

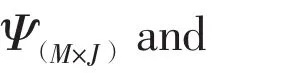
The number of expansion terms is increased incrementally using J=J+1.The process described above is repeated to obtain the relative error under the condition J=J+1 again.

A set of relative errors related to the truncation number of the expansion modes will befinally obtained by traversing J from 1 to N.The truncation number of the expansion modes corresponding to the minimum value of the relative errors should be chosen as the optimal expansion term Jop.Then,substituting Jopinto the above separation process,the optimal results of sound separation will be obtained.

2 Numerical simulation

2.1 Two rigid pulsating balls disposed oppositely around the measurements

Simulations are carried out to investigate the validity of the proposed FST based on acoustic radiation modes.A test case with two rigid pulsating spheres not located at symmetrical positions was examined.As depicted in Fig.3,the centre of the rigid pulsating sphere as the target source was located at(0,0.05 m,0),whose radius and vibration velocity were 0.05 m and 0.08 m/s,respectively.The radius and vibration velocity of another rigid pulsating sphere located at(-0.05 m,0,0.3 m)were 0.05 m and 0.16 m/s,respectively.The pressure was measured in a grid of 6×6 points with 0.04 m interspacing at the hologram,centre of which was (0,0,0.1 m).In numerical calculations,the sound was transmitted through the air,and its velocity was set to 343 m/s.The theoretical values of the measurement plane were calculated according to the radiation induced by a rigid pulsating sphere[21].In order to obtain simulation results closer to the actual measurements,a random white noise with an intensity of 30 dB was added to the simulated an actual measurement.

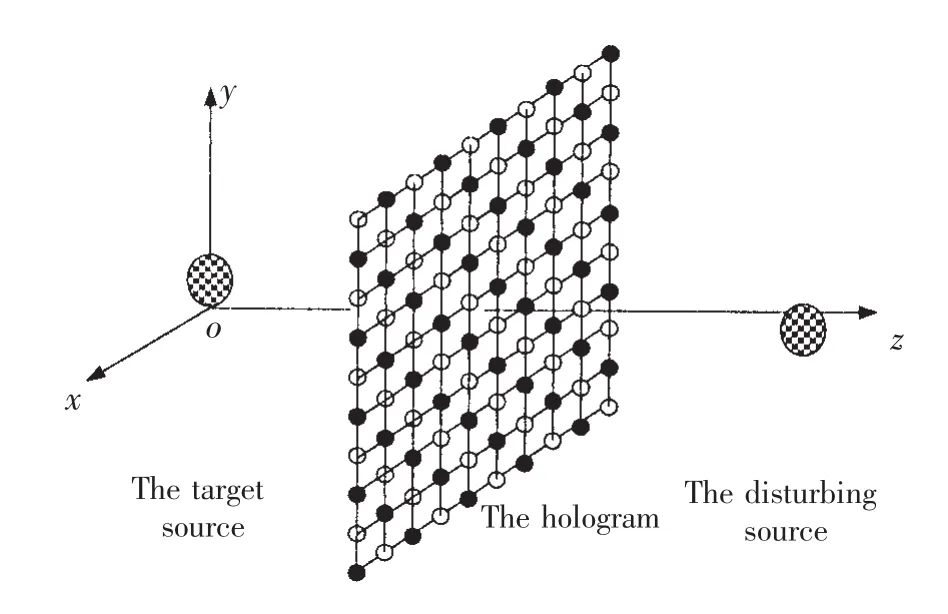
Fig.3 The spatial distribution diagram of the target source,disturbing source and hologram

Fig.4 The first nine acoustic radiation modes of the rigid pulsating ball

The acoustic radiation modes of the rigid pulsating ball are needed for initial calculations before the FST process.The results can be obtained using Eq.(6).When the exciting frequency is 546 Hz,the first nine acoustic radiation modes are shown in Fig.4.

By performing the proposed separation method,the pressure radiated by the target source and disturbing source can be separated effectively.Considering the number of the measurement points is large,the pressure at the measurement points which are selected every two from the first one of the first column is compared.Fig.5 shows the amplitudes and phase of the total pressure,recovered free-field radiated pressure and theoretical pressure radiated by the targetsource on the measurement plane for f= 546 Hz.

There is a large difference between the total pressure and the theoretical pressure,as depicted in Fig.5.After the separation process,the recovered free-field radiated pressure on the measurement plane shows good agreement with its theoretical values.According to Eq.(15),the relative errors between the amplitude and phase of the recovered pressure and theoretical pressure are just 2.46%and 3.5%, respectively.

In order to further verify the universal applicability of the proposed method, the relative errors of the amplitudes corresponding to different frequencies(109.2 Hz to 982.6 Hz)were calculated.

Fig.6 shows the relationship between the relative errors and frequency.The measurement errors are always above 80%,which demonstrates that the total pressure is seriously corrupted by the disturbing radiation,and therefore it cannot be used to replace the free-field radiated pressure.By performing the proposed separation step,the free-field pressure radiated by the target source was successfully recovered. Here,all of the separation errors are below 10%(some were even smaller,e.g.,the separation error at 464 Hz was 1.9%),which further demonstrates the validity of the proposed separation method.

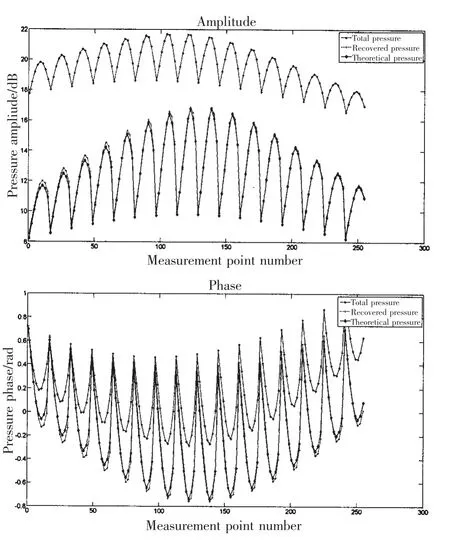
Fig.5 The amplitudes and phase of the total pressure, recovered pressure and theoretical pressure

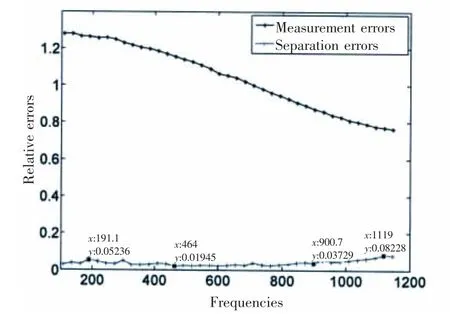
Fig.6 The relative errors of the amplitudes

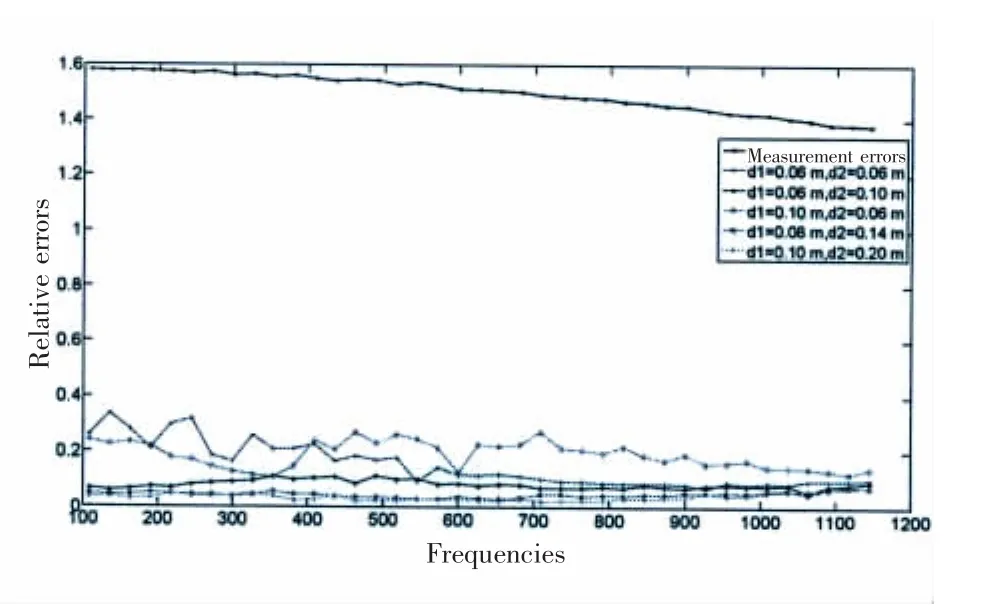
Fig.7 The relative errors with different distances between the sources and the measurement

Fig.7 gives the relative errors as a function of distances between target source-to-hologram d1 and disturbing source-to-hologram d2.The spatial distribution diagram and other parameters,as shown in Fig.3 are used.Note that the measurement errors are so large(owing tothe influence of the disturbing source)that the separation errors are,in comparison,smaller. However,the distances are different,the separation error curves showed the similar tendency, which means the applicability of the proposed method in the general case.

SNR(Signal to Noise Ratio,SNR)which illustrates the source strength comparison of the target source and the disturbing source is a key parameter influencing the separation accuracy.By changing the vibration velocities of the sources,relative errors with different SNR can be obtained,as shown in Fig.8.

Fig.8 shows the separation errors as a function of SNR between the target source and the disturbing source.The results indicate that the errors increase as the parameter SNR decreases.This is not surprising,considering the fact that the interference of the disturbing source on the measurement plane is stronger when SNR becomes smaller.However,even SNR decreases to-8,somewhat ideal results still can be obtained which means the proposed method has good anti-disturbance property.

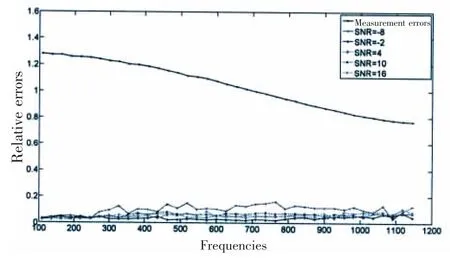
Fig.8 The separation errors with different SNR

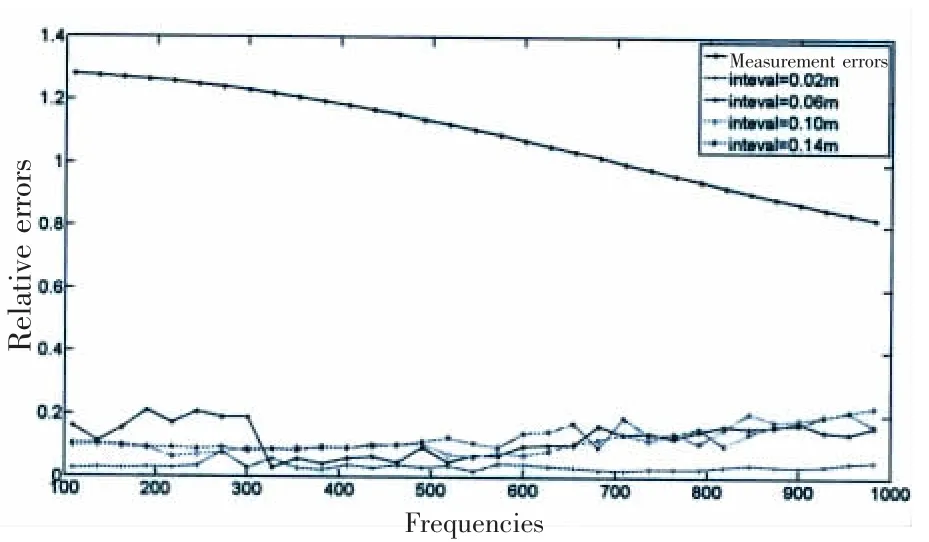
Fig.9 The separation errors with different measurement intervals

Fig.9 shows the overall separation errors as a function of the measurement interval between two nearby measurement points.As is known,smaller the measurement interval is,more likely the interval satisfies the sampling theorem and more accurate measurement information can be obtained.However,the interval becomes larger,the separation errors are still in the acceptable range.

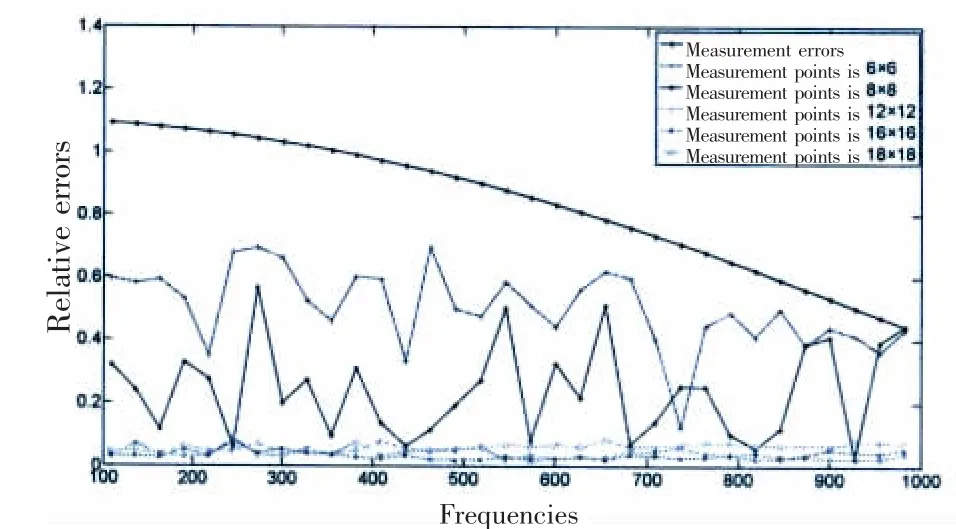
Fig.10 The separation errors with different measurement points

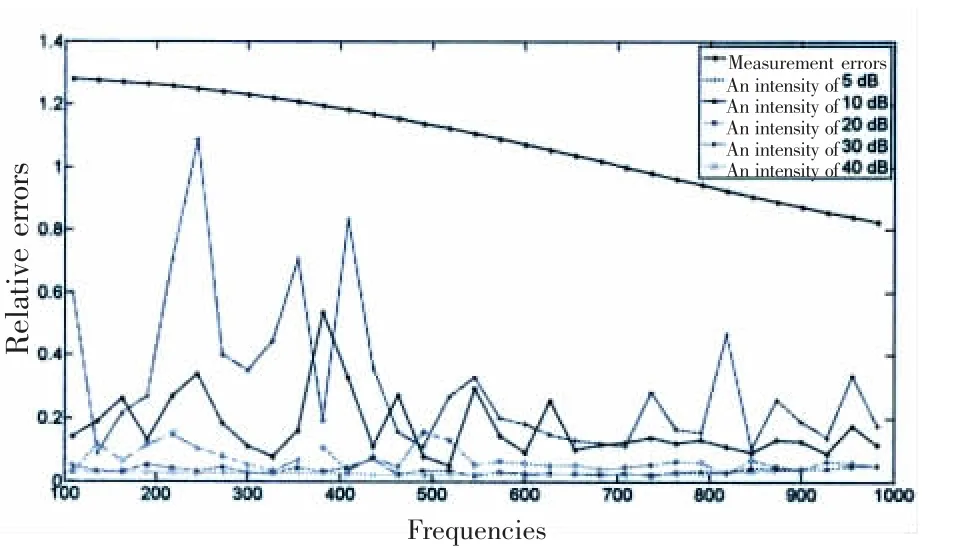
Fig.11 The separation errors affected by a random white noise with different intensities

Fig.10 illustrates the separation errors as a function of the measurement points.It shows when the measurement points are fewer,enough field information could not be measured whichleads to high separation errors.As more measurement points are used,the separation errors reduce rapidly.When the measurement points increase to 12×12,ideal results have been obtained and the separation errors would not vary obviously which means just 12×12 measurement points are needed to satisfy the measurement requirement.

As the effect of a random white noise with intensity of 30 dB is considered in the foregoing studies,Fig.11 shows the separation errors affected by a random white noise with different intensities.It shows that the random white noise with low value of the intensity would affect the validity of the proposed separation method.However,as the value of the intensity is selected to 20 or over,the effect of the random noise would be eliminated availably by the proposed method.

2.2 Plate disturbed by a rigid pulsating ball

Two sources with different modal expansion are then studied for the universality of the proposed FST.The target source was a simple supported steel plate,dimensions of which are 0.5 m×0.5 m and 0.008 m thick,centered at the origin of coordinates.The disturbing source was a rigid pulsating ball with a radius of 0.05 m and a vibration velocity of 0.08 m/s,placed opposite to the target source,located at(0,0,0.14 m).The pressure was measured in a grid of 16×16 points at the hologram with the dimension(1 m×1 m),centered at(0,0,0.06 m).In the numerical calculation,the sound was transmitted through the air,and its velocity was set to 343 m/s.The excitation of the plate was a harmonic force with an amplitude 100 N.The exciting frequency for the plate is set at 600 Hz and the force is located at(0.125 m,0.125 m, 0)(corresponding modal frequency is 612 Hz).The theoretical values on the hologram radiated by the plate could be obtained using the Rayleigh integral method based on FFT[22].Random white noise was added to the simulated measurements with an intensity of 30 dB.

Fig.12 shows the total pressure,theoretical pressure without disturbance,and the recovered pressure on the hologram for f=600 Hz.The total pressure as depicted in Fig.12(a)shows a large difference from the theoretical pressure as depicted in Fig.12(b).By performing the proposed method,the agreement between the separated results as depicted in Fig.12(c)and their theoretical values as depicted in Fig.12(b)is very good.The measurement error and separation error were 100.93%and 5.12%,respectively.

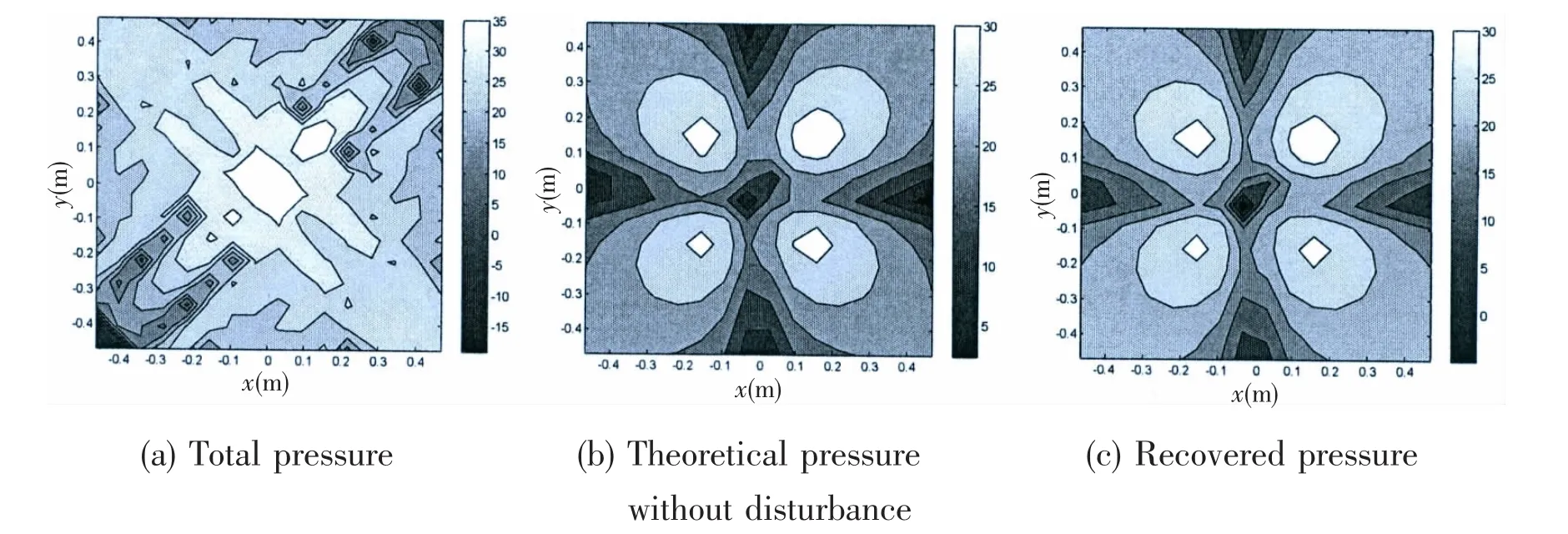
Fig.12 Pressure in decibels on the hologram for f=600 Hz

Tab.1 gives the relative errors,measurement errors and separation errors,for different exciting frequency,which demonstrates the ability of the separation procedure to recover the free field and to suppress the influences of the disturbing sources.Note that at the measurement errors are so large that the free-field radiated pressure is,in comparison,very small,which makes the relative error become relatively large in the presence of finite measurement noise.However,all the relative errors are below 10%

3 Conclusions

In this paper,the acoustic radiation modes were used for all these purposes in order to eliminate the influence of disturbances.By applying a sound field separation technique based on a single measurement plane,the pressures radiated by the target source and the disturbing source can be separated.As only one layer microphone array is needed,the measurement cost and time could be reduced visibly.Numerical simulations were carried out to test the method. Five parameters such as distances between target source-to-hologram and disturbing sourceto-hologram,source strength comparison of the target source and the disturbing source,measurement interval between two nearby measurement points,the number of measurement points and random white noise with different intensities which would affect the validity of the proposed method were investigated in details.All the results prove the effectiveness and accuracy of the proposed method.The satisfactory results obtained on simulations give hope for the characterization of real sources in non-free spaces.Measurements have been in progress and would be reported in the near future.

Acknowledgments

The authors gratefully thank the supports from Natural Science Foundation of China (grants 51305452),and express their thanks to the referees for their review of this manuscript.

[1]Williams E G,Dardy H D,Fink R G.Nearfield acoustical holography using an underwater,automated scanner[J].J A-coust.Soc.Am.,1985,78(2):789-798.

[2]Bi C X,Bolton J S.An equivalent source technique for recovering the free sound field in a noise environment[J].J A-coust.Soc.Am.,2012,131(2):1260-1270.

[3]Cheng M T,Mann J A,Pate A.Sensitivity of the wave-number domain field separation methods for scattering[J].J A-coust.Soc.Am.,1996,99(6):3550-3557.

[4]Bi C X,Hu D Y,Zhang Y B,et al.Reconstruction of the free-field radiation from a vibrating structure based on measurements in a noisy environment[J].J Acoust.Soc.Am.,2013,134(4):2823-2832.

[5]Bi C X,Hu D Y,Xu L,et al.Recovery of the free field in a noisy environment by using the spherical wave superposition method[J].Acta Acust.,2014,39(3):339-346.

[6]Jacobsen F,Chen X Y,Jaud V.A comparison of statistically optimized near field acoustic holography using single layer pressure-velocity measurements and using double layer pressure measurements[J].J Acoust.Soc.Am.,2008,123(4): 1842-1845.

[7]Fernandez-Grande E,Jacobsen F.Sound field separation with a double layer velocity transducer array[J].J Acoust.Soc. Am.,2011,130(1):5-8.

[8]Langrenne C,Melon M,Garcia A.Boundary element method for the acoustic characterization of a machine in bounded noisy environment[J].J Acoust.Soc.Am.,2007,121(5):2750-2757.

[9]Jacobsen F,Jaud V.Statistically optimized near field acoustic holography using an array of pressure-velocity probes[J]. J Acoust.Soc.Am.,2007,121(3):1550-1558.

[10]Zhang Y B,Chen X Z,Jacobsen F.A sound field separation technique based on measurements with pressure-velocity probes[J].J Acoust.Soc.Am.,2009,125(6):3518-3521.

[11]Bi C X,Zhang Y B,Xu L,et al.An experimental investigation of planar nearfield acoustic holography using pressure and particle velocity measurements[J].Acta Phys.Sin.,2010,59(2):1108-1115.

[12]Elliott S J.Radiation modes and the active control of sound power[J].J Acoust.Soc.Am.,1995,94(4):2194-2204.

[13]Cunefare K A,Currey M N.On the exterior acoustic radiation modes of structure[J].J Acoust.Soc.Am.,1994,96(4): 2302-2312.

[14]Borgiotti G V.The power radiated by a vibrating body in an acoustic fluid and its determination from boundary measurment[J].J Acoust.Soc.Am.,1990,88(4):1884-1893.

[15]Williams E G.The nearfield acoustical holography(NAH)experimental method applied to vibration and radiation in light and heavy fluids[J].Comput.Struct.,1997,65(3):323-335.

[16]Song L,Koopmann G H,Fahnline J B.Active control of the acoustic radiation of a vibrating structure using a superposition formulation[J].J Acoust.Soc.Am.,1991,89(6):2786-2792.

[17]Cunefare K A.The minimum multimodal radiation efficiency of baffled finite beams[J].J Acoust.Soc.Am.,1991,90(5): 2521-2529.

[18]Cunefare K A,Currey M N.On the exterior acoustic radiation modes of structure[J].J Acoust.Soc.Am.,1994,96(4): 2302-2312.

[19]Hansen P C.Rank-Deficient and Discrete Ill-posed Problems.Numerical Aspects of Linear Inversion[M].Philadelphia: SIAM,1998:1-127.

[20]Wu S F,Rayess N,Xiang Z.Visualization of acoustic radiation from a vibrating bowling ball[J].J Acoust.Soc.Am., 2000,109(6):2771-2779.

[21]Wang Z,Wu S F.Helmholtz equation-least squares method for reconstructing the acoustic preesure field[J].J Acoust. Soc.Am.,1997,102(4):2020-2032.

[22]Williams E G,Maynard J D.Numerical evaluation of the rayleigh integral for planar radiators using the FFT[J].J A-coust.Soc.Am.,1982,72(6):2020-2023.

基于声辐射模态理论的声场分离技术

郭亮a，b，朱海潮a，b，毛荣富a，b，苏俊博a，b，陈志敏c
（海军工程大学a.船舶与噪声研究所；b.船舶振动噪声重点实验室；c.动力工程学院，武汉430033）

为了消除复杂声场中干扰噪声对于近场声全息重建精度的影响，该文提出了一种基于单层阵列测量的声场分离技术。当目标声源和干扰噪声源为相干声源时，利用源强密度声辐射模态分析理论建立了声源与辐射声场的数学关系模型，通过对单层阵列测量的声压数据进行空间重采样得到两组子数据，构造各组子数据与目标声源和干扰噪声源的声辐射模态之间的数学公式，再求解公式中目标声源的各阶声辐射模态的展开系数，可重构目标声源在阵列处的声场响应，达到声场分离的目的。刚性脉动球声源与刚性脉动球干扰源、平板声源与刚性脉动球干扰源的数值仿真及对影响该方法的相关参数进行了详细研究，相关结果表明该方法具有较好的有效性和正确性。

声辐射模态；单层阵列；声场分离技术；近场声全息

O42

:A

国家自然科学基金资助项目（51305452）

郭亮（1987-），男，海军工程大学振动与噪声研究所博士研究生；

O42

:A

10.3969/j.issn.1007-7294.2017.06.012

1007-7294（2017）06-0779-12

朱海潮（1963-），男，海军工程大学振动与噪声研究所教授；

毛荣富（1982-），男，海军工程大学振动与噪声研究所讲师；

苏俊博（1985-），男，海军工程大学振动与噪声研究所博士研究生；

陈志敏（1979-），男，海军工程大学动力工程学院讲师。

date：2017-01-27

Supported by the National Natural Science Foundation of China(Grant No.51305452)

Biography：GUO Liang(1987-),male,Ph.D.candidate,corresponding author,E-mail:hgliangg@163.com; ZHU Hai-chao(1963-),male,professor.