广义正交性点态性质的量化差异的几个结论

李万涛， 孙剑明，李 芳

(1. 哈尔滨商业大学 基础科学学院 哈尔滨 150028；2. 哈尔滨商业大学 计算机与信息工程学院，哈尔滨 150028；3. 大连交通大学 动车运用与维护工程学院 大 连 116028)



广义正交性点态性质的量化差异的几个结论

李万涛1， 孙剑明2，李 芳3

(1. 哈尔滨商业大学 基础科学学院 哈尔滨 150028；2. 哈尔滨商业大学 计算机与信息工程学院，哈尔滨 150028；3. 大连交通大学 动车运用与维护工程学院 大 连 116028)

等腰正交和Birkhoff正交之间存在着量化差异，为了刻画这种差异，引入了几何常数，对这个几何常数的相关性质进行研究，给出了几个结论.

等腰正交；Brikhoff正交；可达性

在经典的欧氏几何中，角度的概念非常重要，并且将“所有直角均相等”作为其理论基础中的第四共设.相应地，得到了许多与正交性相关的重要结论，如著名的毕达哥拉斯定理.在推广的Hilbert空间理论中，将内积为零的元对定义为是正交的.但是，在更加广泛的Banach空间几何理论中，既没有角度的概念，又没有内积的概念，正交性概念的推广就成为非常重要的研究方向.因此，许多广义正交性概念被提了出来[1-4]，并取得了一些成果[5-9].本文对用以刻画广义正交性点态性质差异的几何常数D(X)[10]进行研究，解决了D(X)的可达性，二维序列空间中的D(X)连续性与单调性等问题.

1 定义

在对正交性概念的推广过程中，出现了Birkhoff正交、Singer正交、等腰正交、面积正交等各种广义正交性，Birkhoff正交和等腰正交因其定义形式简洁、几何背景直观而得到了较为广泛的研究.

1935年，美国数学家G·Birkhoff基于“点到直线的线段中垂线段最短”这一性质，引入了Birkhoff正交的概念：

定义1 设X是一个赋范线性空间，x,y∈X，如果对任意的α∈R， 都有

‖x+αy‖≥‖x‖

则称xBirkhoff正交于y，记为x⊥By.

R· C·James基于“线段中垂线上的点到线段两个端点的距离相等”这一性质，提出了等腰正交的概念：

定义2 设X是一个赋范线性空间，x,y∈X，如果它们满足

‖x+y‖=‖x-y‖

则称x等腰正交于y，记为x⊥Iy.

在一般的赋范线性空间中，等腰正交和Birkhoff正交是不一致的，这种差别在不同的赋范线性空间中也有很大的差异，为了精细地对这种差别给出一个的数量的刻画，计东海和吴森林引入了几何常数D(X)：

定义3

并给出了D(X)的上下界

2 下界的可达性

在Banach空间几何理论中，引入几何常数之后，很自然的问题就是其上下界是否可达，在文献[11]中，已经给出了其上界D(X)=1的可达性的结论，因此D(X)的下界是否可达问题引起了同行学者的关注.

为解决D(X)下界的可达性问题，我们引入文献[11]中的结论：对于任一Banach空间X，dim(X)≥2，存在e1,e2∈S(X)，使得e1⊥Ie2，并且

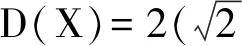
借助赋范数的直和运算，我们构造D(X)不可达的空间.为确保严格凸性质对赋p范数的直和运算的传递性，给出引理：

证明 对于x,y∈lp(Xi)，不妨设x与y线性无关，令

x=(x(1),x(2)，…，x(i),…),y=(y(1),y(2),…,y(i),…)则有

(*)

只需证明式中两个“≤”中有一个为严格“<” 即可.

已知x=(x(1),x(2),…,x(i),…)与y=(y(1),y(2),…,y(i),…)线性无关，讨论x(i)与y(i)的关系：

1)若∃i∈N，使得x(i)与y(i)线性无关，则在Xi中，x(i)与y(i)线性无关且Xi严格凸，有‖x(i)i‖i+‖y(i)i‖i>‖x(i)+y(i)‖，即(*)式中第一个“≤” 为严格“<”， 结论成立.

2)若对∀i∈N，若x(i)与y(i)均线性相关，即有

x=(x(1),x(2),…,x(i),…)，

y=(k1y(1),k2y(2),…,kiy(i),…)

且由x与y线性无关， 则至少存在

i,j∈N,ki≠kj,x(i)≠x(j)

考虑

x′=(‖x(1)‖，‖x(2)‖，…,‖x(i)‖，…),y=(|k1|‖y(1)‖，|k2|‖y(2)‖，…,|ki|‖y(i)‖，…)

由ki≠kj， 有两种情况：

i)若|ki|≠|kj|， 则x′与y′线性无关， 由Minkowski不等式“=”成立条件，有(*)式中第二个“≤”为严格“<”；

ii)若|ki|=|kj|，又ki≠kj， 故ki=-kj.不妨取i=1,j=2,x(i)≠x(j)≠0，

则x=(x(1),x(2),…,x(i),…) y=(ky(1),-ky(2),…,ky(i),…)(k>0)

x+y=((1+k)x(1),(1-k)x(2),…(1+ki)x(i),…)，且

(1)

另外

(2)

比较式(1)，(2)可得(1)<(2)，即

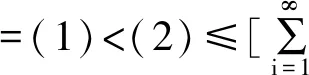
证毕

证明 每个Xi={R2,‖·‖pi}都是二维序列空间，显然是严格凸的，从而由引理1，X 为严格凸空间；另一方面，由X的构造方法及D(X)定义， 有

且对任意Banach空间，有

定理2 已知F(t,p)是关于t,p的连续函数， 则

F(t,p)-F(t,p0)|<ε

又

由于

又

-ε<-|F(t,p)-F(t,p0)|≤F(t,p)-F(t,p0)≤|F(t,p)-F(t,p0)|<ε

同理

故

同理

从而对上述∀t∈I，p0，∀ε>0 ，∃δ>0，使得当|p-p0|<δ时，有

|f(p)-f(p0)|<ε

f(p)关于p连续，即

证毕.

证毕

定理4 对于

有如下结论：

1)若1≤p≤r≤2， 则

2)若2≤p≤r<∞， 则

B=((p-1)3tp+t2q+p+tq+2p(3-3p+p2)tpq+(p-1)3t(p+1)qlnt

因此， gt(p)在[1,2]为单调上升的“又对p∈[1,2]，有gt≤gt(2)=1， 则对p[1,2]” 有

即ft(p)在[1,2]是单调递减的， 对于1≤p≤r≤2， 有

同理， 可得对2≤p≤r≤∞

证毕

有

Ft(p)≤Ft(r)

(*)

证毕

[1]BIRKHOFFG.Orthogonalityinlinearmetricspaces[J].DukeMath.J., 1935 (2): 169-172.

[2] JAMES R C. Orthogonality in normed linear spaces [J]. Duke Math. J., 1945, 4(4): 297-318.

[3] ROBERTS B D. On the geometry of abstract vector spaces [J]. Tohoku Mathematical Journal, 1934, 39: 42-59.

[4] SINGER I.Unghiuri abstractes si functii trigonometrice in spatii banach[J].Acad.Repub1.Popul.Eomine,1957(9):29-42.

[5] CARLSSON S O. Orthogonality in normed linear spaces [J]. Ark. Mat., 1962, 4: 297-318.

[6] DIMINNIE C R. A new orthogonality relation in normed linear spaces [J]. Math. Nachr., 1983, 114 (1): 197-203.

[7] ALONSO J, BENITEZ C. Area orthogonality in normed linear spaces [J]. Arch. Math., 1997, 68(1): 70-76.

[8] JAMES R C. Orthogonality and linear functionals in normed linear space [J]. Trans. Amer. Math. Soc., 1947, 61(2): 265-292.

[9] AMIR D. Characterzations of inner product spaces [J]. Birkhuser Verlag,1986,4(1):1-6.

[10] DAY M M. Some characterizations of inner product spaces [J]. Trans. Amer. Math. Soc., 1947(62): 320-337.

[11] JI D, WU S. Quantitative characterization of the difference between birkhoff orthogonality and isosceles orthogonality [J]. J. Math. Anal. Appl., 2006, 323(1): 1-7.

Point-wise difference between generalized orthogonalities

LI Wan-tao1, SUN Jian-ming2, LI Fang3

(1. School of Basic Science, Harbin University of Commerce, Harbin 150028, China; 2. School of Computer and Information Engineering, Harbin University of Commerce, Harbin 150028, China; 3. School of Motor Vehicle Operation and Maintenance Engineering, Dalian Jiaotong University， Dalian 116028, China)

There is quantitative difference between Birkhoff orthogonality and isosceles orthogonality. In order to characterize the quantitative difference, this paper introduced the geometric constantD(x). Obtained some results aboutD(x).

isosceles orthogonality;Birkhoff orthogonality; attainability

2017-03-01.

国家自然科学基金项目(11171082)；黑龙江省哲学社会科学项目 (15TQ05);哈尔滨商业大学实践教学改革与研究项目(SJXM2017B001)

李万涛(1976-)，男，硕士，教师， 研究方向：泛函分析.

O174

A

1672-0946(2017)03-0332-04