带被动踝关节的双足机器人动力学及步态研究

孙欣然，臧希喆，刘义祥，林珍坤

(哈尔滨工业大学 机器人技术与系统国家重点实验室，哈尔滨 150001)



带被动踝关节的双足机器人动力学及步态研究

孙欣然，臧希喆，刘义祥，林珍坤

(哈尔滨工业大学 机器人技术与系统国家重点实验室，哈尔滨 150001)

欠驱动双足步行机器人是仿人机器人领域研究的热点之一.针对带有被动踝关节的双足机器人，建立了五杆四驱动模型，对模型进行动力学分析.根据拉格朗日原理，建立机器人单足支撑动力学模型和基于碰撞的双足支撑动力学模型.建立完整的欠驱动双足步行机器人动力学模型.对机器人步态进行了规划.规划了欠驱动机器人的时不变步态；利用贝塞尔多项式拟合出虚拟约束的轨迹，给出了欠驱动机器人轨迹规划的算法；采用极限环方法，通过验证庞加莱回归映射不动点稳定性，验证了极限环的稳定性，从而验证了机器人步态的稳定性.

欠驱动；双足机器人；动力学；步态规划

人类研究机器人已经有了很长一段历史，而研制出与人类外形相似，功能相似的机器人一直是研究者们的愿望.仿人机器人可以从事枯燥，危险的工作，同时又比人类具有更高的效率和耐力，不必考虑一些身体或心理上的问题，可谓人类完美的替身.在这样的背景下，仿人机器人这一研究领域成为国内外研究者、学者们的研究热点.从20世纪60年代开始，开始出现仿人机器人.相比于其他种类的机器人，仿人机器人的发展十分迅猛.除了机器人学之外，对仿人机器人的研究还涵盖了力学、生物学、控制科学、甚至心理学等不同的学科，逐渐成为了一个多学科交叉的独特研究领域.以双足步行为主要运动形式的一类仿人机器人具有很高的灵活性，能够适应不同的地形，是仿人机器人领域里一个重要的分支[1-4].

但一个为人熟知的问题是，双足步行机器人结构上一般具有很高的复杂度，性能上速度也比较慢，尤其是在要求高负载的情况下.过去50年，国内外许多研究机构都对双足步行机器人的结构设计和运动控制做出了大量研究，但是机器人的能源和效率问题并没有得到很好的解决.双足机器人要想获得敏捷的性能，需要具有很好的地面适应性和稳定性，要想获得持久的耐力，需要具有高效节能的关节结构和控制方法.实际上基于计算机的足部自主运动控制器从1970年开始就引起了研究者的兴趣.但是基于轨迹生成与追踪的传统步态控制器，对于降低机器人的功耗并不是一个很好的选择[5-6].

传统的双足步行机器人每个自由度都由一个执行元件驱动，根据人类双足的运动特点，生成一条各个关节的运动轨迹，通过控制执行元件动作来精确地追踪这条轨迹，完成类似人类双足的运动方式.本课题追随的是一种新的趋势，研究含有主动关节和被动关节的双足步行机器人，也就是欠驱动双足步行机器人.本课题研究的机器人踝关节是被动关节，这种结构更符合人类的双足步行特点，具有被动踝关节的结构可以提高机器人对地面的适应性[7-9].

1 欠驱动机器人动力学分析

在动力学分析中，建立如图1所示模型，模型包括躯干、两条大腿、两条小腿共5个杆件.躯干和大腿之间有两个主动自由度，大腿和小腿之间有两个主动自由度，所以机器人结构中一共有4个驱动，称其为“五杆四驱动模型”.由于踝关节是被动关节，在足与地面接触时，相当于足与地面成为一体，所以可以将机器人的足简化成点足来研究.

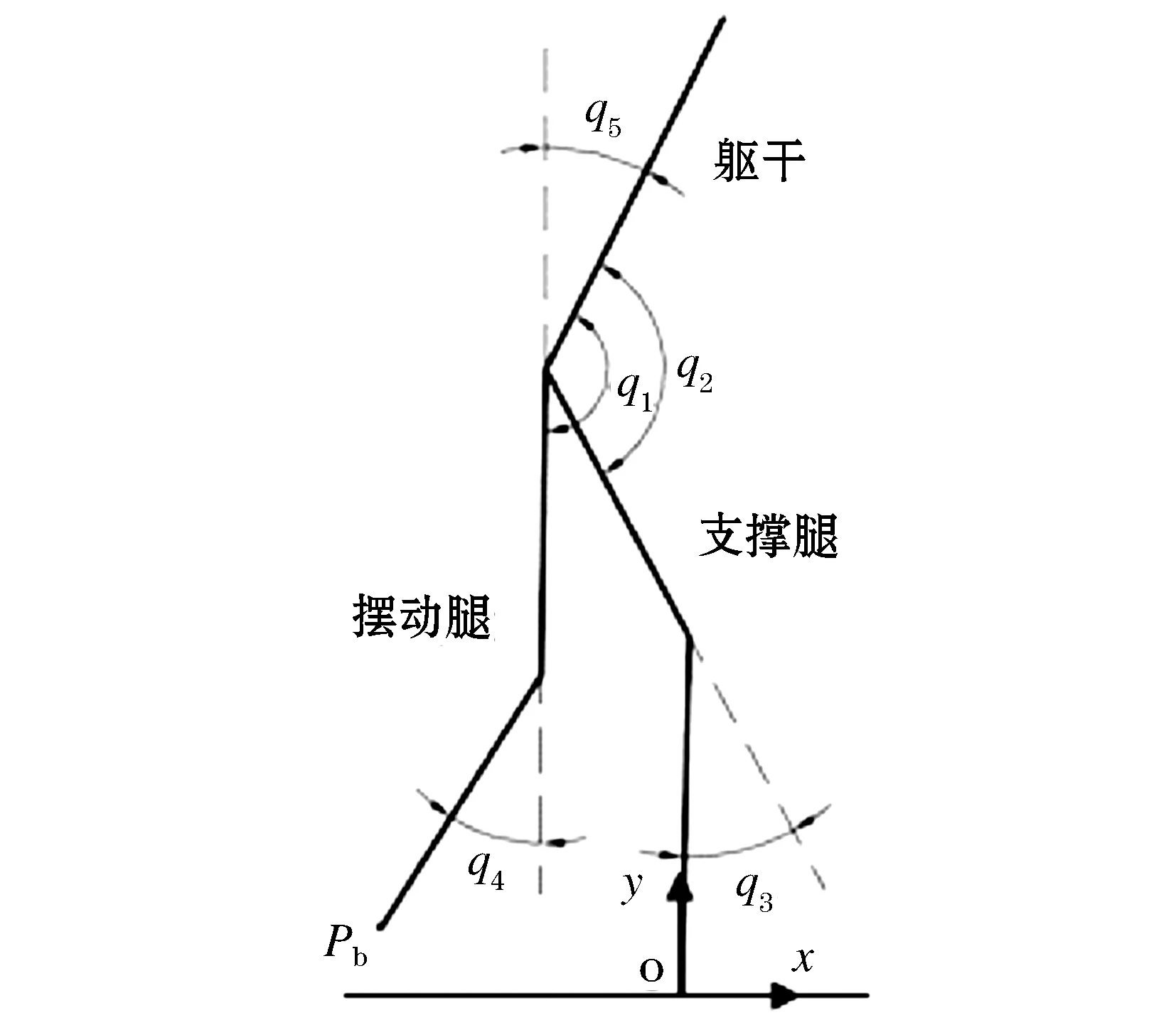
图1 机器人动力学分析结构模型

在进行动力学分析之前，需要先说明欠驱动机器人的结构模型(五杆四驱动模型)所基于的假设条件：

1)由5个刚性连杆和4个理想转动关节(刚性无摩擦)组成，形成一个开放运动链.此外每个杆件都有质量，且质量是分散式的；

2)运动是二维的，且关节的运动都约束在矢状面内；

3)双足形式，两足对称分布在躯干两侧，足和躯干的连接点称为髋关节，足末端是一个点；

4)4个驱动互相独立；

5)支撑足与地面的接触点处是被动的踝关节没有驱动.

本文研究双足机器人在平面上的匀速步行.机器人的结构只有躯干和双足，忽略了头、手的影响.机器人步行过程可以归纳为周期运动，即摆动腿从后方摆到前方并接触地面变为支撑腿，然后支撑腿离开地面变为摆动腿，两腿按照一定周期不断交替运动.为了使机器人可以实现周期性的步行运动，其步行控制器需要具备以下特性.

1)分为单腿支撑和双腿支撑两个支撑相，且二者交替进行；

2)在单腿支撑时，支撑足是一个理想的旋转中心点，即在支撑足与地面接触的整个过程中，与地面接触力的垂直分量始终为正，水平分量不超过静摩擦力大小；

3)双足支撑发生在一瞬间，相应的地面接触可以看作刚性接触；

4)摆动腿落地时，不会打滑也不会弹回.支撑腿离地时不会与地面有相互作用；

5)在稳定状态时，两条腿的运动是对称的；

6)机器人每一步，都是严格地开始于摆动腿从支撑腿后方摆动到支撑腿前方并与地面接触；

7)步行顺序从左腿到右腿，在水平面上进行.

摆动腿与地面的接触是一种冲击，这种冲击可以假设为两个刚体的碰撞.已有的刚体碰撞理论可以根据摆动腿与地面碰撞前的运动参数，得到二者碰撞之后摆动腿的运动参数.本文采用的刚体碰撞理论需要基于以下假设：

1)冲击是足底完全接触并终止于地面的结果；

2)冲击是瞬间发生的；

3)发生冲击时，外部施加的作用力可以看作是脉冲力；

4)关节驱动无法形成脉冲力，因此在发生冲击时可以被忽略；

5)机器人的速度可以因为脉冲力而发生突变，而机器人的位姿不会因为脉冲力发生突变.

1.1 单腿支撑阶段动力学模型

根据结构模型假设条件1，机器人模型是一个开环运动链，根据步行假设条件5，双腿的运动是关于髋关节对称的.所以机器人的两条腿在作为摆动腿时，运动参数是相同的，对一条腿进行分析即可.根据基于能量的拉格朗日原理，对于6自由度的机器人，可列出方程

动能方程中，机器人的运动参数是各杆件在固定坐标系中的速度和角速度，而拉格朗日方程中的运动参数是各关节角度及其导数.为了将动能以关节运动参数来表示，需要建立雅克比矩阵将固定坐标系中的运动参数转化为相对坐标系中的运动参数.

可写为

动能表达式可以简化为

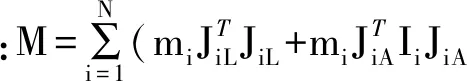
机器人各杆件势能之和为机器人总势能，表达式为

其中:pi3为杆件i质心所在位置的纵坐标.列出拉格朗日方程，

有

其中:

1.2 双腿支撑阶段动力学模型

在摆动腿接触地面产生冲击时，地面会给足的末端点一个反作用力，此时末端点不能再看作是只有一个自由度的铰链，而是可以在矢状面内产生平动的点，所以需要在固定坐标系中引入新的坐标，那么对于6自由度的机器人，各杆件的位姿变量为qe=[q;Pb].将新的位姿变量带入拉格朗日方程得到，

=Be(qe)τ+δFext

上式可化简为

双腿支撑阶段增加的坐标Pb在单腿支撑阶段可以由关节角度q得到，记为

Pb=γe(q)

因此，

摆动腿与地面发生碰撞时，由步行运动假设4，摆动腿既不弹回也不发生滑动，所以摆动腿末端坐标与支撑腿末端相同，都是Pb，利用虚功原理，

综上分析，可以得到

解得

其中:

综上推导，已知碰撞前状态的条件下，可以计算出碰撞后摆动腿末端的速度和地面对其作用力.至此，机器人的行走动力学模型已经建立完毕.机器人动力学模型由摆动阶段和碰撞阶段组成，其中摆动阶段是在一段时间内的连续过程，而碰撞阶段发生在一瞬间，是离散过程.两种过程按周期交替出现就构成了连续和离散的混杂模型.两种过程产生切换的时刻是在摆动腿触地的一瞬间，此时摆动腿末端横坐标Pb_h大于0，纵坐标Pb-v等于0，可以归纳为

S={x|Pb_v=0,Pb_h>0}

那么机器人的完整动力模型为

2 欠驱动机器人步态规划

2.1 时不变步态规划

为了让机器人按照一定周期做步行运动，需要对机器人的参考轨迹hd(θ(q))进行规划.规划的过程实际上就是把hd(θ(q))进行参数化的过程.参数化过程需要用到贝塞尔多项式.四驱动机器人具有四维参考轨迹，令

hd(θ)=[b1(s)b2(s)b3(s)b4(s)]T

有

贝塞尔多项式是平滑曲线，其本身、导数和二阶导数在始末点都易于计算，即碰撞前后的状态表达非常方便.端点值如下：

1)多项式端点值

bi(0)=α(i,0)

bi(1)=α(i,M)

2)一阶导数端点值

3)二阶导数端点值

对于欠驱动双足步行机器人，为了得到贝塞尔多项式的周期解，需要满足以下边界条件：

基于上一节的完整动力学模型以及本节的贝塞尔多项式分析，可以总结出欠驱动机器人的步态规划步骤：

2)由碰撞方程式，计算碰撞后的运动参数：

3)建立贝塞尔多项式

4)验证多项式轨迹是否能形成稳定的步态.

2.2 时不变步态稳定性分析

下面对稳定性分析加以说明.与传统的纯主动机器人不同，欠驱动机器人的步行运动是动态过程，其稳定性不能再用ZMP方法来判定，而应该使用一种适合动态运动的稳定性判定方法来进行分析.欠驱动机器人的运动不要求每个时刻都是稳定的，只要求步行运动能够按周期持续.

本文采用极限环方法来保证机器人步行运动的稳定性.欠驱动双足步行机器人按一定周期运动，机器人的状态每隔一个周期循环一次，其在状态空间里表现为周期性轨迹，即极限环.极限环方法基于庞加莱回归映射原理(PRM).庞加莱映射中极限环与超平面的交点收敛于任一交点邻域内时，极限环稳定，这个点叫做不动点.所以混杂零动态的稳定性可以转化为对庞加莱映射不动点的求解.

庞加莱回归映射定义为：

xk+1=P(xk)=φ(xk,γ(xk))

极限环稳定性等价于庞加莱回归映射不动点稳定性.

图2 机器人周期行走极限环

3 结 语

本文分析机器人足部结构，建立了带有柔性关节双足步行机器人的“五杆四驱动”结构模型；基于拉格朗日原理，建立了带有柔性关节的欠驱动机器人的单腿支撑动力学模型；基于有接触力项的拉格朗日方程和虚功原理，建立了带有柔性关节的欠驱动机器人双腿支撑动力学模型. 利用贝塞尔多项式规划了机器人的欠驱动步态；利用绘制极限环方法，找到了机器人不动点，验证了机器人步行运动的稳定性.

[1] HÜRMÜZLÜY, MOSKOWITZ G D. The role of impact in the stability of bipedal locomotion [J]. Dynamics and Stability of Systems, 1986, 1(3): 217-234.

[2] MANOONPONG P, KULVICIUS T, WÖRGÖTTER F,etal. Compliant ankles and flat feet for improved self-stabilization and passive dynamics of the biped robot “RunBot”[C]//Humanoid Robots (Humanoids), 11th IEEE-RAS International Conference on. IEEE, 2011: 276-281.

[3] SHIH C L, GRIZZLE J W, CHEVALLEREAU C. Asymptotically stable walking of a simple underactuated 3D bipedal robot[C]//Industrial Electronics Society, 2007. IECON 2007. 33rd Annual Conference of the IEEE. IEEE, 2007: 2766-2771.

[4] CHEVALLEREAU C, GRIZZLE J W, SHIH C L. Asymptotically stable walking of a five-link underactuated 3-D bipedal robot [J]. IEEE Transactions on Robotics, 2009, 25(1): 37-50.

[6] HANAZAWA Y, YAMAKITA M. Limit cycle running based on flat-footed passive dynamic walking with mechanical impedance at ankles[C]//Advanced Intelligent Mechatronics (AIM), 2012 IEEE/ASME International Conference on. IEEE, 2012: 15-20.

[7] HüRMüZLüY Y, MOSKOWITZ G D. The role of impact in the stability of bipedal locomotion [J]. Dynamics and Stability of Systems, 1986, 1(3): 217-234.

[8] KUSANO K, ZHARIF M, UCHIMURA Y. Variable compliance control with posture stabilization for biped robot[C]//Mechatronics (ICM), 2015 IEEE International Conference on. IEEE, 2015: 410-415.

[9] MAJIDI C. Soft robotics: a perspective—current trends and prospects for the future [J]. Soft Robotics, 2014, 1(1): 5-11.

Dynamics analysis and gait planning of biped robot with underactuated ankle

SUN Xin-ran,ZANG Xi-zhe, LIU Yi-xiang, LIN Zhen-kun

(State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150001, China)

The underactuated biped walking robot is one of the hotspot in research of humanoid robot. Aimed at biped robot with a passive ankle, the five-bar model was established. The model of dynamics analysis was introduced. According to the principle of Lagrangian, single support dynamics model was established and also the double support dynamics model based on collision. The complete underactuated biped walking robot dynamics model was established. And introduced the robot gait planning. Planned the time-invariant gait of the underactuated robot. By using Bessel polynomial，this paper fitted out the trajectory of virtual constraint. And gave the algorithm of the underactuated robot gait planning. Used the limit cycle method to verify the Poincare return-mapping fixed point’s stability. The stability of the limit cycle was also proved. Verified the stability of the robot gait.

underactuated; biped robot; dynamics; gait planning

2016-06-22.

国家重点实验室自主课题(SKLRS201304B)

孙欣然(1991-)，男，硕士，研究方向：仿人双足机器人.

TP242

A

1672-0946(2017)03-0319-05