函数易错题分析
2017-06-21马爱平
文/马爱平
函数易错题分析
文/马爱平
责任编辑:王二喜
在解有关函数问题时,我们会出现一些错误.现把常见的错误列举出来,并加以分析,希望你能从中吸取教训,避免犯类似的错误.
一、没有掌握对称点的坐标特征
例1(2016年成都卷)平面直角坐标系中,点P(-2,3)关于x轴的对称点的坐标为( )
A.(-2,-3). B.(2,3). C.(-3,2). D.(3,-2).
错解:B.
剖析:P(-2,3)关于x轴的对称点是(-2,-3).选A.
温馨小提示:点(x,y)关于x轴对称的点是(x,-y),关于y轴对称的点是(-x,y),关于原点对称的点是(-x,-y).
二、忽视自变量的取值范围
例2(2016年齐齐哈尔卷)点P(x,y)在第一象限内,且x+y=6,点A的坐标为(4,0).设△OPA的面积为S.在下列图象中,能正确表示面积S与x之间的函数关系式的图象是( )
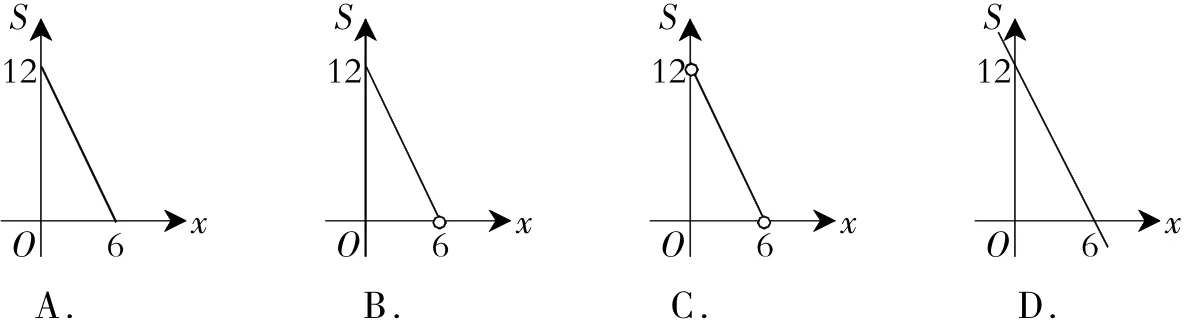
错解:选D.
剖析:本题中的自变量x和S都具有实际意义,图象必在第一象限内.
∵点P(x,y)在第一象限内,且x+y=6,∴y=6-x(0<x<6,0<y<6).
温馨小提示:在实际问题中,自变量的取值范围会受到限制,所以对应的图象可能是原函数图象的一部分.
三、求自变量取值范围时顾此失彼
A.x>3. B.x≥3. C.x>4. D.x≥3且x≠4.
错解:选B.
剖析:错解只考虑到二次根式的被开方数必须大于等于0,没有注意分母不能为零,应是x-3≥0,且x-4≠0,∴x≥3且x≠4.选D.
温馨小提示:自变量x必须满足两个条件:一是二次根式有意义,二是分式有意义.
四、审题错误
例4(2016年菏泽卷)小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,加快了骑车速度.下面是小明离家后他到学校剩下的路程s关于时间t的函数图象,那么符合小明行驶情况的图象大致是( )
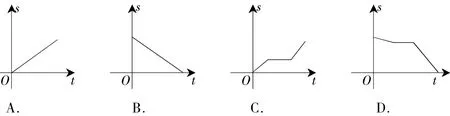
错解:选C.
剖析:在选项C中,s是小明离家的路程,其实s表示小明离家后他到学校剩下的路程.事实上,小明家离学校有一段路程,图象不可能经过原点,排除A和C.开始是用正常速度匀速行驶,时间增加,路程不断减小,图象是一条倾斜的线段;修自行车这一段时间,时间增加,路程没变,图象是一条平行于x轴的线段;车修好后加快了骑车速度,相距的路程s随着时间t的增加而快速减少,线段的倾斜程度变“陡”.选D.
五、没有对函数解析式分类讨论
例5(2016年荆州卷)若函数y=(a-1)x2-4x+2a的图象与x轴有且只有一个交点,则a的值为_____.
错解:∵函数y=(a-1)x2-4x+2a的图象与x轴有且只有一个交点,
∴Δ=16-4(a-1)×2a=0,解得a1=-1,a2=2.故a的值为-1或2.
剖析:它可以是二次函数,也可以是一次函数,漏掉了后一种情况.
正解:(1)当a≠1时,同上解,可得a1=-1,a2=2;
(2)当a=1时,此时y=-4x+2,它的图象与x轴也有且只有一个交点,满足要求.
因此a的值为-1或2或1.
温馨小提示:对于含字母系数的函数问题,要注意对解析式分类讨论.
六、利用反比例函数的性质解题时没有分象限
例6(2016年天津卷)若点A(-5,y1),B(-3,y2),C(2,y3)在反比例函数的图象上,则y1,y2,y3的大小关系是( )
A.y3>y1>y2. B.y1>y2>y3. C.y2>y1>y3. D.y3>y2>y1.
错解:∵k=3>0,∴y随x的增大而减小,而-5<-3<2,∴y1>y2>y3.选B.
剖析:反比例函数的性质是分象限研究的,当k>0时,图象在同一个象限内,y随x的增大而减小.错解忽视了这一点.其实由-5<-3<0,只能得到y1>y2;再由y1,y2都小于0,而y3大于0,有y3>y1>y2.选A.
温馨小提示:应用反比例函数的性质解题时一定要注意分象限研究.本题还可分别求出y1,y2,y3的值为,所以y3>y1>y2.也可以画出反比例函数的图象,借助于图象可得y3>y1>y2.
七、平移错误
例7(2016年泰安卷)将抛物线y=2(x-1)2+2向左平移3个单位,再向下平移4个单位,那么得到的抛物线的表达式为______.
错解:y=2(x-4)2-2.
剖析:抛物线y=a(x-h)2+k的平移就是顶点的平移,将点(h,k)向左平移m个单位得(h-m,k),此时抛物线为y=a(x-h+m)2+k,因此原抛物线向左平移3个单位后y=2(x-1+3)2+2=2(x+2)2+2,再向下平移4个单位,所以y=2(x+2)2+2-4=2(x+2)2-2.
温馨小提示:二次函数图象的平移,实质上是顶点坐标的平移,只要确定平移前后的顶点坐标,就可以写出平移后的解析式.
八、点的坐标与线段长度的转化错误
例8(2016年鄂州卷)二次函数y=ax2+bx+c的图象如图1,点C在y轴的负半轴上,且OA=OC,则( )
A.ac+1=b B.ab+1=c C.ac+1=-b D.以上都不是
错解:当x=0时,y=ax2+bx+c=c,则C(0,c),∵OA=OC,
∴A(c,0),∴ac2+bc+c=0,∴ac+b+1=0,即ac+1=-b,选C.
剖析:由图象可知,点C在y轴的负半轴上,因此其纵坐标应该为负数,即c<0;点A在x轴的正半轴上,即点A的坐标为(-c,0).

图1
正解:当x=0时,y=ax2+bx+c=c,则C(0,c).
∵点C在y轴的负半轴上,∴c<0.
∵OA=OC,∴OA=|c|.
又点A在x轴的正半轴上,
∴A(-c,0),∴a·(-c)2+b·(-c)+c=0,∴ac-b+1=0,
即ac+1=b.选A.
温馨小提示:要注意线段长与点的坐标的相互转化.由点的坐标求线段长需要加绝对值,由线段长求点的坐标要注意符号.
九、重复计算重叠部分的面积
例9(2016年包头卷)一幅长20cm、宽12cm的图案,如图2,其中有一横两竖的彩条,横、竖彩条的宽度比为3∶2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
(1)求y与x之间的函数关系式;
剖析:由图2可知,三条彩条的面积=横彩条的面积+2条竖彩条的面积-横竖彩条重叠矩形的面积.
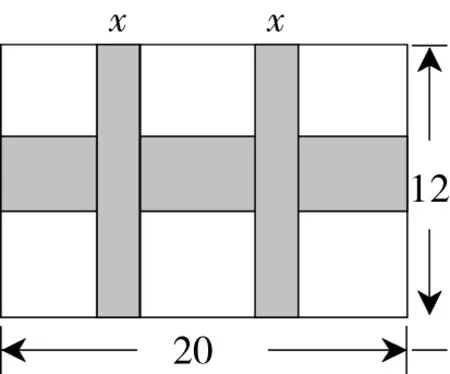
图2

(2)根据题意得-3x2+54x=×20×12,
即x2-18x+32=0,∴x1=2,x2=16(舍去),

答:横彩条的宽度为3cm,竖彩条的宽度为2cm.
温馨小提示:解决问题时,可运用图形的变换,将三条彩条平移到边上,则y=20×12-=-3x2+54x,即可避免上述错误.
