怎样解答数学选择题
2017-06-21刘洋
文/刘洋
怎样解答数学选择题
文/刘洋
责任编辑:王二喜
解初中数学选择题的方法很多,技巧性较强,需要根据题目的特点,灵活选择解法,才能快速得到答案.解选择题的常用方法有下面几种.
一、直接法
从题目的条件出发,通过运算或推理,直接求得结论.

二、排除法
选择题因其答案是四选一,必然有一个正确答案.根据题设和有关知识,排除三个不正确的选项,那么剩下的便是答案.如果只能排除一个或两个错误的选择,不能立即得到答案,至少可以缩小选择范围,提高解题的准确率.
例2(2016年张家界卷)在同一平面直角坐标系中,函数y=ax+b与y=ax2-bx的图象可能是( )

解析:选项A,由直线y=ax+b的图象可得,a>0,b>0;而对于抛物线y=ax2-bx来说,对称轴0,应在y轴的右侧,两图象矛盾,排除选项A.
选项B,由直线y=ax+b的图象可得,a<0,b>0;而对于抛物线y=ax2-bx来说,对称轴<0,应在y轴的左侧,两图象矛盾,排除选项B.
选项C,由直线y=ax+b的图象可得,a>0,b>0;而对于抛物线y=ax2-bx来说,图象开口向上,对称轴,在y轴的右侧,符合题意.
选项D,由直线y=ax+b图象可得,a>0,b>0;而对于抛物线y=ax2-bx来说,图象开口向上,两图象矛盾,排除选项D.选C.
温馨小提示:根据一次函数图象确定a、b的符号,进而判断另一个函数的图象是否符合题意.解题的关键是熟练掌握一次函数、二次函数图象与其系数之间的关系.
三、验证法
将四个选项分别代入题设中检验,从而确定答案.
例3(2016年新疆卷)如图1,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≅△DEF,这个条件是( )
A.∠A=∠D. B.BC=EF.
C.∠ACB=∠F. D.AC=DF.
解析:∵∠B=∠DEF,AB=DE,
若添加∠A=∠D,利用ASA可得△ABC≅△DEF;
若添加BC=EF,利用SAS可得△ABC≅△DEF;
若添加∠ACB=∠F,利用AAS可得△ABC≅△DEF.
故选D.
温馨小提示:验证法的优点是题目条件容易把握,分析判断有根据,一到两次的验证就能得到正确答案,准确率高.缺点是若分析判断不准确,就需要验证三次,计算和推理量大.
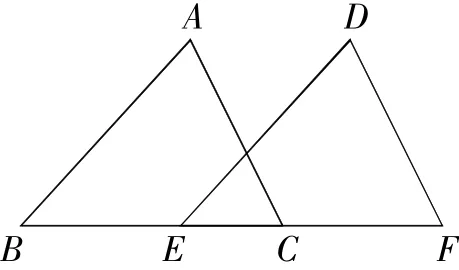
图1
四、特殊值法
选取某个符合条件的特殊值或作出特殊图形进行计算或推理,从而得到正确答案.此类问题通常具有一个共性:题干中给出一般性的条件,而要求得出某些特定的结论或数值.
A.y1<y2<0. B.y1<0<y2. C.y1>y2>0. D.y1>0>y2.
解析:因为x1<0<x2,取x1=-1,x2=1,代入得,y1=1,y2=-1,
∴y1>0>y2.选D.
温馨小提示:用取特殊值法解题时,所选的值要符合条件,且易于计算.
五.数形结合法
经过简单的计算或推理,结合图形、图象的直观性进行判断,从而找出正确答案.
例5(2016年济南卷)如图2,若一次函数y=-2x+b的图象交y轴于点A(0,3),则不等式-2x+b>0的解集为( ).

解析:∵一次函数y=-2x+b的图象交y轴于点A(0,3),
∴b=3,
观察函数图象,可知:当x,
温馨小提示:根据函数图象上的点,确定b的值是解题的关键.

图2
六、转化法
通过观察、分析、类比、联想,将未知转化为已知、将抽象转化为具体的一种解题方法.
例6(2016年桂林卷)如图3,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是( )
A.x=2. B.x=0.
C.x=-1. D.x=-3.
解析:方程ax+b=0的解,就是直线y=ax+b与x轴交点的横坐标,
∵直线y=ax+b过B(-3,0),
∴方程ax+b=0的解是x=-3.选D.
温馨小提示:直线y=ax+b与x轴的交点的横坐标,它是方程ax+b=0的解.

图3
七、估算法
估算法适用于选择题.通过对数据进行估算,再与选择项比较,从而确定正确答案.
例7(2016年毕节卷)如图4,正方形ABCD的边长为9,将正方形折叠,使顶点D落在BC边上的点E处,折痕为GH.若BE∶EC=2∶1,则线段CH的长是( )
A.3. B.4. C.5. D.6.
解析:解法一:设CH=x,则DH=EH=9-x,
∵BE∶EC=2∶1,BC=9,


图4
在Rt△ECH中,EH2=EC2+CH2,
即(9-x)2=32+x2,
解得x=4,即CH=4.
选B.
解法二:∵BE∶EC=2∶1,BC=9,
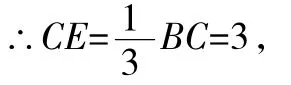
在Rt△CEH中,由于EH是斜边,
所以EH>EC,即EH>3,
又EH=DH,EH>CH,
而DH+CH=9,可知CH<5.
若CH=3,则EH=DH=6,EC=3,EH、HC、EC不能构成三角形.
选B.
温馨小提示:这类考题主要不在“算”,而在“估”,不追求数据的精确,而追求方法的正确.
