无证书聚合签名方案的分析与改进

徐明明，尹毅峰*，张 晴，刘 扬，王佳星

(1.郑州轻工业学院 计算机与通信工程学院，郑州 450001；2.河南机电职业学院，郑州 451191)



无证书聚合签名方案的分析与改进

徐明明1，尹毅峰1*，张 晴1，刘 扬1，王佳星2

(1.郑州轻工业学院 计算机与通信工程学院，郑州 450001；2.河南机电职业学院，郑州 451191)

聚合签名技术在资源受限的场景下有很好的应用，是数字签名研究中的热点.对最近提出的一个无证书聚合签名方案进行安全性分析，指出方案不能抵抗伪造性攻击.提出改进的的无证书聚合签名方案，在随机预言模型和Computational Diffie-Hellman(CDH)困难假设下，证明了改进的方案的不可伪造性，效率分析对比表明，改进的方案更安全高效.

无证书密码体制；聚合签名；不可伪造性

2003年，Al-Riyami等[1]提出了无证书公钥密码体制，解决了传统公钥密码体制中的证书管理和密钥存储问题.Boneh等[2]在2003年首次提出了聚合签名的概念.聚合签名把多个不同的签名压缩成一个签名，接收者只需要验证聚合签名，就可以验证签名的有效性.聚合签名减少了通信资源和存储资源的消耗，提高了验证签名的效率，在无线通信领域和物联网中有着广泛的应用.无证书聚合签名方案利用了无证书公钥加密方案和聚合签名方案两者的优势，增强安全性，提升效率.近些年，学者们提出了许多无证书聚合签名方案[3-13].杜红珍等[3]利用双线性对提出了一个可证安全的无证书聚合签名方案，并认为在CDH困难假设和随机预言机模型下，方案是存在性不可伪造的.然而，通过对该方案进行安全分析，发现敌手可以伪造出有效的签名，方案不满足不可伪造性.针对这个缺点，本文提出改进的无证书聚合签名方案，并在随机预言模型和CDH困难假设下，证明了改进的方案是存在性不可伪造的.

1 背景知识

1.1 双线性对

设q是一个大素数，G1是阶为q的加法群，G2是阶为q的乘法群.P是G1的一个生成元.存在映射函数e∶G1×G1→G2，有以下三条性质：

1)可计算性：对于任意的P,Q∈G1，存在有效的算法可以计算出来e(P,Q)；

3)非退化性：e(P1,P2)≠1.

1.2 CDH困难问题

CDH困难：对于a,b∈Zq，给定P,aP,bP∈G1，计算abP∈G1.

1.3 无证书聚合签名方案

根据文献[13]的描述，无证书聚合签名方案通常包括初始化，部分密钥提出，用户密钥生成，签名，聚合和签名验证6个部分.

1)初始化：输入参数k，输出系统的主密钥s和系统参数params；

2)部分私钥提取：输入s，params和用户的身份IDi，输出用户部分私钥dIDi；

3)用户密钥生成：输入params和用户的身份IDi，生成用户秘密值xi和相应的用户公钥pkIDi；

4)签名：输入params和信息mi，用户秘密值xi，用户公钥pkIDi和用户部分私钥dIDi，生成相对应的签名δi；

5)聚合：输入n个用户的用户身份IDi，信息mi，用户公钥pkIDi和签名δi，然后生成一个聚合签名δ；

6)签名验证：输入params，聚合签名δ和用户身份IDi，信息mi和用户公钥pkIDi，验证聚合签名δ是否可用.

1.4 无证书聚合签名敌手类型

在无证书聚合签名方案中有两种类型敌手：敌手AI和敌手AII.敌手AI：可以替换用户的公钥，但是不能获取系统的主密钥.敌手AII：可以获取系统的主密钥，但是不能替换用户的公钥.

2 文献[3]方案安全性分析

最近杜红珍等[3]提出了一个高效的可证明安全的无证书聚合签名方案，本节首先简要回顾其方案，然后对方案进行安全性分析.

2.1 文献[3]方案回顾

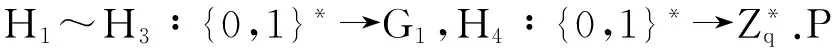
2)部分私钥提取：对身份IDi，KGC计算Qi=H1(IDi)和部分私钥dIDi=sQIDi.

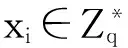
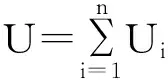
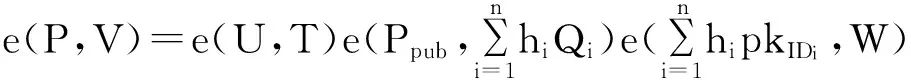
2.2 文献[3]方案安全性分析

杜红珍等[3]认为方案在适应性选择消息攻击下是存在性不可伪造的，本文分析发现敌手A可以任意创建出用户IDi对于消息mi的可用签名.攻击的具体过程展示如下：

1)A运行配置算法获得系统参数params，系统主密钥s和系统公钥Ppub.

2)A分别计算T=H2(Ppub)，W=H3(Ppub)，hi=H4(mi,IDi,pkIDi)，dIDi=sQIDi.

3)A创建用户获取公钥pkIDi.

4)A分别计算Ui=-hipkIDiW/T，Vi=hidIDi.

可以验证伪造的签名δi=(Ui,Vi)是有效的签名，因为

e(Vi,P)=e(hidIDi,P)=e(hisQIDi,P)=

e(Ppub,hiQIDi)e(hipkIDi,W)e(hipkIDi,W)-1=

e(Ppub,hiQIDi)e(hipkIDi,W)e(hipkIDiT/T,W)-1=

e(Ppub,hiQIDi)e(hipkIDi,W)e(-hipkIDiW/T,T)=

e(Ppub,hiQi)e(hipkIDi,W)e(Ui,T)

且敌手A的攻击满足三个条件：①签名(Ui,Vi)有效；②没有替换公钥；③没有询问部分私钥.因此A的攻击是有效的.

3 改进的无证书聚合签名方案

为了解决上节中的问题，本节提出了改进的无证书聚合签名方案.本方案将Ui置于Hi中，并且调整了Vi的组成.敌手在构造Ui时，要先计算出Hi，而Hi中又包含Ui，不能计算出Ui，Hi.从而使敌手不能使用上节中的方法伪造签名.改进方案如下：

2)部分私钥提取：对身份IDi，KGC计算Qi=H1(IDi)和部分私钥dIDi=sQIDi.

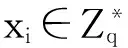
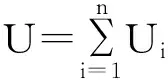
4 安全性分析

4.1 正确性分析

由下式成立可知，本方案是正确的.

4.2 安全性证明

定理1 在CDH困难假设和随机预言机模型下，改进的无证书聚合签名方案在敌手AI的适应性选择消息攻击下是存在性不可伪造的.

证明：设第一类敌手AI询问H1，H2，H3，H4和部分私钥询问，公钥询问和签名询问的次数分别是qH1，qH2，qH3，qH4，qdID，qpsk，qs.假设敌手AI以不可忽略的优势ε伪造出签名，则存在一种挑战S可以利用AI解决CDH难题.

初始化：S运行初始化算法生成系统参数params={k,e,G1,G2,Ppub,H1,H2,H3,H4}，令Ppub=sP，并把params发给敌手AI.

执行下面的询问，其中列表L1，L2，L3，L4分别对应对H1，H2，H3，H4的询问：

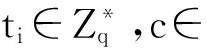
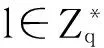
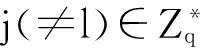
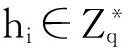
5)部分私钥询问：当AI询问IDi的部分私钥时，S查询L1中的记录(IDi,Qi,ti,c).若c=1，退出.否则，计算dIDi=ti(aP)，返回dIDi并添加(IDi,dIDi)到表Lpsk中.

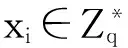
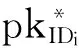
8)签名询问：当AI询问(mi,IDi)的签名时，S分别查询记录(IDi,Qi,ti,c)，(Ppub,l,T)和(P,Ppub,j,W).若c=0，S查询记录(mi,IDi,pkIDi,Ui,hi).S选择随机数ri并计算Ui=riP-QIDi)和Vi=riT+hixiW+riPpub.返回δi=(Ui,Vi)给AI.δi是一个可用的签名，因为

e(Vi,P)=e(riT+hixiW+riPpub,P)=

e(riT+hixiW+risP,P)=

e(riT+hixiW+s(Ui+QIDi),P)=

e(Ui,T)e(Ppub,Qi+Ui)e(hipkIDi,W)

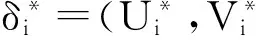
算法S满足以下条件：S部分签名询问没有失败；AI以概率ε伪造出了有效的签名.且算法S成功的概率

Pr(S)≥ε(1-(qdID/(qdID+1))n)(qdID/(qdID+1))qdID+qs

定理2 在CDH困难假设和随机预言机模型下，改进的无证书聚合签名方案在敌手AII的适应性选择消息攻击下是存在性不可伪造的.

证明：假设敌手AII以不可忽略的优势ε伪造出签名，则存在一种挑战者S可以利用AII解决CDH难题.

初始化：令Ppub=sP，生成系统参数params={k,e,G1,G2,Ppub,H1,H2,H3,H4}，将系统参数params和主密钥s发给AII.S执行以下询问：

1)H1询问：当AII输入IDi是，S查询列表L1，若L1中有记录(IDi,Qi,ti)，返回Qi.否则，S选择随机数ti，另Qi=tiP，返回Qi并添加(IDi,ti,Qi)到列表L1中.

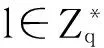
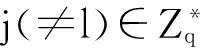
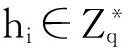
5)部分私钥询问：当询问IDi的部分私钥时，S查询列表L1，并计算dIDi=tisP，返回dIDi并添加(IDi,dIDi)到Lpsk中.

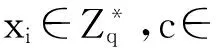
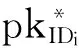
8)签名询问：当询问(IDi,mi)的签名时，S分别查询记录(IDi,Qi,ti,c)，(Ppub,l,T)和(P,Ppub,j,W).若c=0，S查询记录(mi,IDi,pkIDi,Ui,hi).S选择随机数ri，并计算Ui=riP-hixiW/s，Vi=riT+dIDi+riPpub.返回δi=(Ui,Vi)给AII.δi是一个可用的签名，因为：

e(Vi,P)=e(riT+dIDi+risP,P)=e(riT+dIDi+s(Ui+hixiW/s),P)

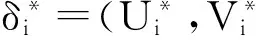
算法S满足以下条件：①S部分签名询问没有失败；②AII以概率ε伪造出了有效的签名.且算法S成功的概率

Pr(S)≥ε(1-(qdID/(qdID+1))n)(qdID/(qdID+1))qpsk+qs

4.3 效率分析

设P表示双线性对运算，M表示标量乘运算，n表示签名用户的数量.本文列出了双线性对运算和标量乘运算两种主要运算，对多个方案的单个签名和聚合签名的计算效率作了对比.

表1 效率比较

由表1可见，本文方案的计算量与方案[3,4,5]相当，但是可以证明是安全的.而和方案[7]相比较，本文新方案计算量更少.

5 结束语

聚合签名减少了通信资源和存储资源的消耗，提高了验证的效率，广泛地应用在无线传感网络中.本文对最近提出的文献[3]方案进行了安全性分析，发现敌手可以任意伪造出有效的签名，方案不能抵抗伪造性攻击.通过调整签名过程中的计算公式和参数，提出了改进的的无证书聚合签名方案.基于CDH困难问题假设，证明了在随机预言模型下改进的方案具有不可伪造性.

[1] AL-RIYAMI S S,PATERSON K G.Certificateless public key cryptography[J].Advances in Cryptology - Asiacrypt 2003,2003,2894:452-473.

[2] BONEH D,GENTRY C,LYNN B,et al.Aggregate and verifiably encrypted signatures from bilinear maps[J].Advances in Cryptology-Eurocrypt 2003,2003,2656:416-432.

[3] 杜红珍,黄梅娟,温巧燕.高效的可证明安全的无证书聚合签名方案[J].电子学报,2013，41(1):72-76.

[4] 喻琇瑛,何大可.一种新的无证书聚合签名[J].计算机应用研究,2014(8):2485-2487.

[5] 陈明.改进的签名长度固定的无证书聚合签名方案[J].计算机应用研究,2016(1):271-275.

[6] 张玉磊,周冬瑞,李臣意,等.高效的无证书广义指定验证者聚合签名方案[J].通信学报,2015，36(2):52-59.

[7] 汤鹏志,郭红丽,张婷婷,等.对一种无证书聚合签名方案的攻击与改进[J].河南师范大学学报(自然科学版),2017,45(1):71-78.

[8] 胡江红,杜红珍,张建中.两类无证书聚合签名方案的分析与改进[J].山东大学学报(理学版),2016,51(7):1-8.

[9] 胡江红,杜红珍,张建中.一个无证书聚合签名方案的分析与改进[J].计算机工程与应用,2016(10):80-84.

[10] 刘丹,石润华,张顺,等.无线网络中基于无证书聚合签名的高效匿名漫游认证方案[J].通信学报,2016,37(7):182-192.

[11] 汤小超,王斌,杨睛,等.一种无证书的顺序聚合签名方案[J].合肥工业大学学报(自然科学版),2015,38(6):775-777.

[12] 许艳,黄刘生,田苗苗,等.一种可证安全的紧致无证书聚合签名方案[J].电子学报,2016,44(8):1845-1850.

[13] XIONG H,LI F,QIN Z G.Certificateless threshold signature secure in the standard model[J].Information Sciences,2013,237:73-81.

[14] HERRANZ J,SAEZ G.Forking Lemmas for Ring Signature Schemes[J].Journal of Management Studies,2003,2904(2):266-279.

责任编辑：高 山

Cryptanalysis and Improvement of Certificateless Aggregate Signature Scheme

XU Mingming1,YIN Yifeng1*,ZHANG Qing1,LIU Yang1,WANG Jiaxing2

(1.College of Computer and Communication Engineering, Zhengzhou University of Light Industry, Zhengzhou 450001, China;2.Henan Mechanical and Electrical Vocational College, Zhengzhou 451191, China)

Aggregate signature technology has a good application in resource-constrained scenarios and is a hotspot in digital signature research.The security of the certificateless aggregate signature scheme proposed by Du et al is analyzed,and we find that the scheme can not resist the forgery attack.Based on the Du scheme,an improved scheme of certificateless aggregate signature is proposed.Under the assumption of stochastic prediction model and Computational Diffie-Hellman (CDH) problem,the unforgeability of the improved scheme is proved,and the efficiency analysis shows that the improved scheme is safer and more efficient.

certificateless cryptography;aggregate signature;unforgeability

2017-03-05.

国家自然科学基金项目(61272038;61572445)

徐明明(1991-)，男，硕士生，主要从事信息安全的研究.*

尹毅峰(1971-)，男，博士，教授，主要从事信息安全与密码学的研究.

1008-8423(2017)02-0190-05

10.13501/j.cnki.42-1569/n.2017.06.018

TP309

A