星体的Lp对偶混合亮度积分

冯丽容

(重庆师范大学 数学科学学院，重庆 401331)



星体的Lp对偶混合亮度积分

冯丽容

(重庆师范大学 数学科学学院，重庆 401331)

引进了所有星体集合上Lp对偶混合亮度积分的概念,同时刻画了Lp对偶混合亮度积分的一些基本性质.

星体; 对偶亮度；Lp对偶混合亮度积分；

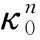
2006年,R J Gardner[1]引进了支撑函数：假定K∈κn则K的支撑函数,hK=h(K,·)：Rn→(-∞,∞)即

hK(u)=h(K,u)=max{(u,x)∶x∈Sn-1},u∈Rn,

(1)

其中(u,x)表示u和x在Rn上的内积.

上世纪Minkowski[2]介绍了凸体的投影体.若K∈κn投影体K定义为具有支撑函数的凸体,对于u∈Sn-1,

h(K,u)=voln-1(K|u⊥),

(2)

其中K|u⊥表示K在经过原点且垂直u的超平面u⊥上的投影.

(3)

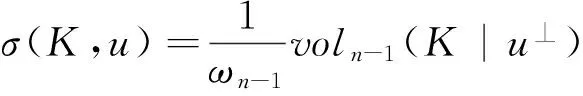
如果Rn上的一个集合是紧集(内部是闭的),则称这个集合是一个体.如果称一个体关于原点是星形的即满足原点与K的边界点的连线段在K的内部.若K是非空,紧的且关于原点是星形的,那么它的径向函数ρK(·)定义[2]如下 ：

ρK(u)=max{λ≥0,λu∈K},

(4)

其中u∈Sn-1使得通过方向的直线u与K相交.

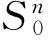
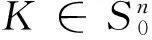
ρ(IK，u)=voln-1(K∩u⊥),u∈Sn-1,

(5)

其中K∩u⊥表示K在经过原点且垂直u的的超平面u⊥的截面.

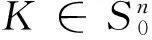
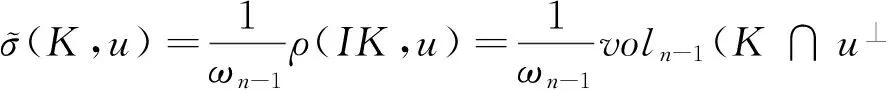
(6)

在本文中,引入了一个新的概念-Lp对偶混合亮度积分,这实际上是关于Lp亮度积分式(3)的对偶形式.

(7)

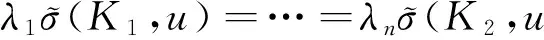
1 准备工作

由式(5),K⊂L当且仅当:

ρ(K,u)≤ρ(L,u),u∈Sn-1.

(8)

显然,对于φ∈GL(n),

(9)

其中φ-1表示φ的逆.

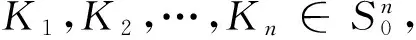
(10)

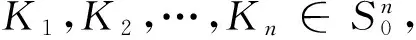
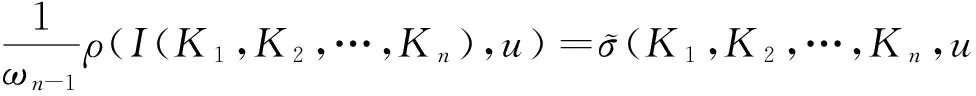
(11)

如果K1=K2=…=Kn-i-1=K,Kn-i=Kn-i-1=…=Kn-1=L, 则有:

I(K1,K2,…,Kn-1)=Ii(K,L).

(12)

假如K1=K2=…=Kn-1=B, 则I(B,B,…,B)=B.

星体K1,K2,…,Kn在方向u上的对偶混合亮度记为:

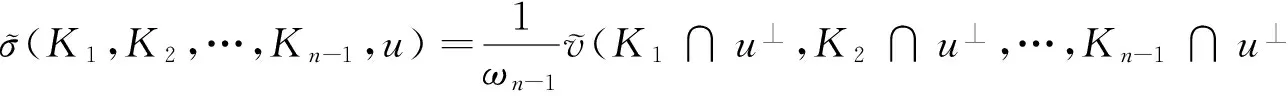
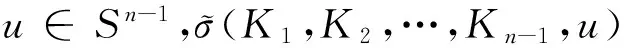
2 星体的对偶混合亮度积分的性质

在本节中,给出了一些星体的对偶混合亮度积分的性质.

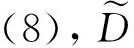
iii)(正齐次性)如果λ1,λ2,…λn≻0, 则:

v)(线性变换下的不变性)如果φ∈GL(n), 则:

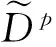
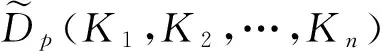
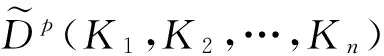
ii)星体K1,K2,…,Kn混合截面体体体积的极坐标公式：

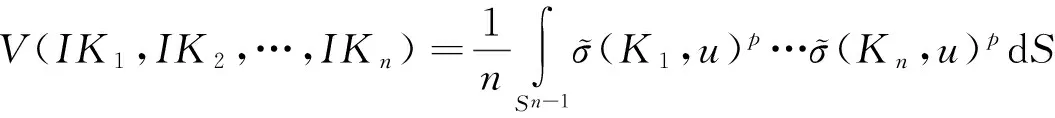
从混合截面体的连续性,可以看到的对偶亮度函数是正的和连续的.因此,混合亮度积分是一个连续函数.

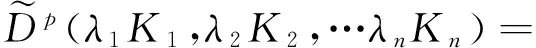
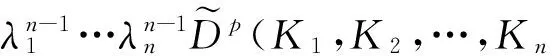
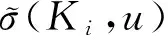
v)由式(7),(10)和(6), 有:

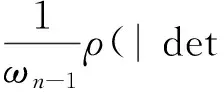
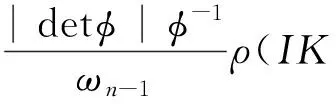
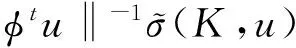
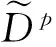
vi)它是Jensen不等式的一个直接结果[13].

[1] GARDNER R J.Geometric Tomography[M].New York:Cambridge University Press,2006.

[2] SCHNEIDER,R.Convex Boides:The Brunn-Minkowski Theory[M].Cambridge:Cambridge University Press,2014.

[3] LI NI, ZHU BAOCHENG.Mixed brightness-integrals of convex bodies[J].J Korean Math Soc,2010,47(5):935-945.

[4] CIANCHI A,LUTWAK E, YANG D,et al.A unified approach to Cramr-Rao inequalities[J].IEEETrans Inform Theory,2014,60:2189-2196.

[5] JUN Y, WING-SUM C.Lp intersection bodies[J].J Math Anal Appl,2008,338:1431-1439.

[6] LUTAWK E.Mixed width-integrals of convex bodies[J].Israel J Math,1977,28(3):249-253.

[7] LU F. Mixed chord-integrals of star bodies[J].Journal of Korean Mathematics Socity,2010,47(2):277-28 .

[8] LUTWAK E.Intersection bodies and dual mixed volumes[J].Advances in Mathematics,1988,71(2):232-261.

[9] CHEN L,ZHAO C.On theL-dual mixed volumes[J].Acta Mathematica Sinica English,2013,29(9):1647-1654.

[10] BERCK G.Convexity ofLp-intersection bodies[J].Advances in Mathematics,2009,222(3):920-936 .

[11] LUTWAK E.Volume of mixed bodies[J].Transactions of the American Mathematical Socity,1986,194(2):487-487.

[12] CIANCHI A,LUTWAK E,YANG D,et al.A unified approach to Cramer-Rao inequalities[J].IEEE Trans Inform Theory,2014,60:643-650.

[13] Hardy H,LITTLEWOOD J E,POLYA G.Inequality[M].Cambridge:Cambridge University Press,1988.

责任编辑：时 凌

LpDual Mixed Brightness-integrals of Star Bodies

FENG Lirong

(School of Mathematical Sciences, Chongqing Normal University, Chongqing 401331, China)

TheLpdual mixed brightness-integrals of star bodies are introduced.Some of their basic properties ofLpdual mixed brightness-integrals of star bodies are discussed.

star bodies;dual mixed brightness;Lpdual mixed brightness-integrals；

2016-11-12.

国家基金自然科学基金面上项目(11271390)

冯丽容(1990-),女,硕士生,主要从事几何分析的研究.

1008-8423(2017)02-0140-03

10.13501/j.cnki.42-1569/n.2017.06.006

B813

A

zhu和Li[3]最近推出的Lp混合亮度积分的经典概念：若K1,K2,…,Kn∈κn,u∈Sn-1,且实数p≠0,K1,K2,…,Kn的Lp混合亮度积分Dp(K1,K2,…,Kn)定义为: