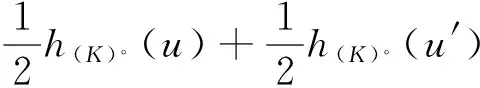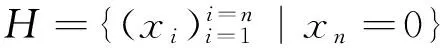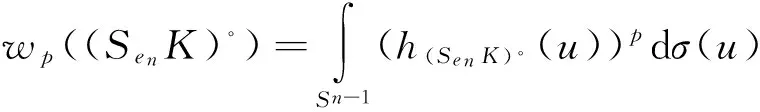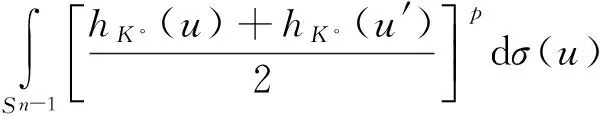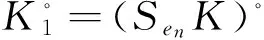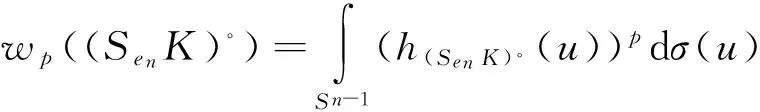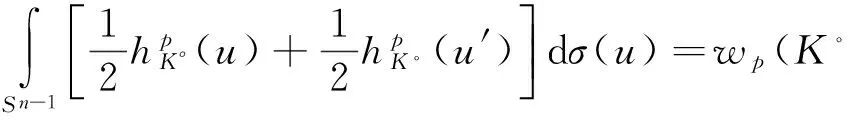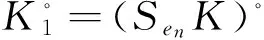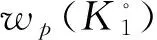极体p平均宽度最值问题的存在性
2017-06-21徐晓琴
徐晓琴
(重庆师范大学 数学科学学院,重庆 401331)
极体p平均宽度最值问题的存在性
徐晓琴
(重庆师范大学 数学科学学院,重庆 401331)
函数在凸体上取最值的研究已经取得了一系列的成果,对于极体而言,是否也有相关结论呢?第一部分介绍了前人在凸体K上的研究,并给出了凸几何中相关知识点的定义.记K∘为K的极体,第二部分证明了研究极体K∘的p平均宽度最值问题是有意义的;p<0时,K∘的p平均宽度取最小值,0 凸体;极体;p平均宽度;存在性 设μ是单位球面Sn-1上的非负伯雷尔测度,如果对于每一个θ∈Sn-1,满足: 其中〈u,θ〉表示u,θ的内积,则称雷尔测度μ在Sn-1上迷向[3-7]. Petty曾研究过最小表面积问题[8],对于Rn中的凸体K,K取最小表面积的充要条件是K的表面积测度迷向,即: 其中:Sn-1表示单位球面;dS(K,·)表示K的表面积测度;S(K)表示K的表面积,且S(K)=S(K,Sn-1). 一个精典的例子是最小平均宽度问题[9],对于Rn中的凸体K,定义平均宽度函数W(K) 其中:K的支撑函数hK(u)=max{〈u,v〉∶v∈K},dσ是Sn-1上旋转不变的概率测度. 在SL(n)作用下凸体K取得最小平均宽度(即∀T∈SL(n),有w(K)≤w(TK)),当且仅当K的平均宽度测度迷向,也即: 另一个例子是最小p平均宽度问题[10],对于Rn中的凸体K,定义p平均宽度函数wp(K) 在SL(n)作用下凸体K取得最小p平均宽度(即对任意的T∈SL(n),有wp(K)≤wp(TK)),当且仅当K的p平均宽度测度迷向,也即: 本文第一部分介绍了K取最小p平均宽度的充要条件是p平均宽度测度迷向;那么对于K的极体K∘而言,研究p平均宽度的最值问题是否有意义呢?文章第二部分证明了研究极体K∘的p平均宽度最值问题是有意义的. 定义1 设X⊂Rn,X的极体X∘[11],满足:X∘={y∈Rn∶〈x,y〉≤1,∀x∈X}. 一般地,设v=en,则凸体K的Steiner对称[12-13]可以表示为: 其中Ken表示K在en上的正交投影. 引理1 设K是以原点为中心的凸体,且中心对称,H是一个通过原点的仿射超平面,则 其中:u=(u1,…,un-1,y)∈Sn-1,u′=(u1,…,un-1,-y),且y∈R. K1={(X,x)|X∈PK,x=(x1-x2)/2,(X,xi)∈K,i=1,2} K∘={(Y,y)∈H×R|〈X,Y〉+xy≤1,X∈PK,x满足(X,x)∈K} 如果A是E的子集,且y∈R,令A(y)={Y∈H|(Y,y)∈A}[14-16].根据Minkowski加法与上面的结论,有: 由上面的结论与u,u′的定义,可得: (1) 定理1 设K是Rn中的凸体,BK∘是Rn的球,且BK∘与K有相同的体积,即|K|=|BK∘|,则 wp(K∘)≥wp(BK∘),p<0 wp(K∘)≤wp(BK∘),0 等式成立当且仅当K∘=BK∘. 证明 先证明对任意的v∈Sn-1,且p<0,在Steiner对称下,p平均宽度Wp单调递减.由引理1,可得: (2) 假设p<0,由式(2),tp的凸性与严格递减以及Wp(K)的定义,可得: 因此: wp((SenK)∘)≤wp(K∘). (3) 也即: wp(K∘)≥wp(BK∘). (4) 其次,当0 因此:wp((SenK)∘)≥wp(K∘). 也即: wp(K∘)≤wp(BK∘). (5) 如果K∘=BK∘式(4)、(5)等号成立.反之,对于p<0时,函数tp严格凸;对于0 [1] BALL K M.Shadows of convex bodies[J].Trans Amer Math Soc,1991,327:891-901. [2] A A GIANNOPOULOS,V D MILMAN.Extremal problems and istropic positions of convex bodies[J].Isael J Math,2000,117:29-60. [3] J BASTERO,M ROMANCE.Positions of convex bodies associated to extremal problems and isotropic measures[J].Adv Math,2004,184:64-88. [4] A A GIANNOPOULOS,M PAPADIMITRAKIS.Istropic surface area measures[J].Mathematika,1999,46:1-13. [5] K BALL.Volume ratios and a reverse isoperimetric inequality[J].J Lond Math Soc,1991,44:351-359. [6] K BALL.Volumes of sections of cubes and related problems[J].Lecture Notes in Math,1989,1376:251-260. [7] V D MILMAN,A PAJOR. Isotropic position and inertia ellipsoids and zonoids of the unit ball of a normed n-dimensional space[J].Lecture Notes in Math,11989,1376:64-104. [8] C M PETTY.Surface area of a convex body under affine transformations[J].Proc Lond Math Soc,1961,12:824-828. [9] A A GIANNOPOULOS,V D MILMAN,M RUDELSON.Convex bodies with minimal mean width[J].Geom Aspects of Funct Anal,Lecture Notes in Math,2000,1745:81-93. [10] J YUAN,G LENG,W CHEUNG.Convex bodies with minimal p-mean width[J].Houston J Math,2010,36:499-511. [11] MARTIN HENK.Convex Geometry Introduction[M].TU Berlin Winter semester,2015,15:2-20. [12] 刘越.Steiner对称化及平面上经Steiner对称化保持直径的凸集[D].广州:中山大学,2009. [13] K LEICHTWEISS.Konvexe Mengen[J].Berlin-Heidelberg-New York,1980. [14] Y GORDON,M MEYER,S REISNER.Zonoids with minimal volume product[J].Proc Amer Math Soc,1988,104:273-276. [15] S REISNER.Zonoids with minimal volume product[J].Math Z,1986,192:339-346. [16] MATHIEU MEYER,ALAIN PAJOR.On the Blaschke-Santaló inequality[J].Arch Math,1990,55:82-93. 责任编辑:时 凌 Existence of the Minimum/Maximum Problem of thepMean Width of Polar Body XU Xiaoqin (School of Mathematical Sciences,Chongqing Normal University,Chongqing 401331,China) The study of taking the min/max value on the convex body by function has achieved a series of results.Are there any related conclusions on the polar body? In the first part of this paper,we introduce the research on the convex body by predecessors and give the definition of the relevant knowledge points in the convex geometry.The second part of the paper proves that the study of polar body'sp-mean width is significant.Ifp<0,thep-mean width of polar body takes the minimum value;If 0 convex body;polar body;p-mean width;existence 2016-11-16. 重庆市研究生科研创新基金项目(CYS16144) 徐晓琴(1993-),女,硕士,主要从事基础数学-凸几何的研究. 1008-8423(2017)02-0137-03 10.13501/j.cnki.42-1569/n.2017.06.005 O18 A1 引言
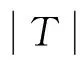
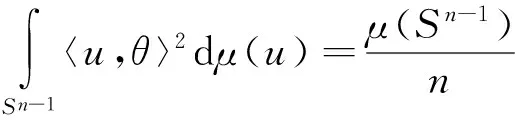
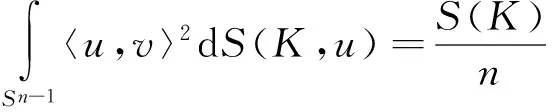



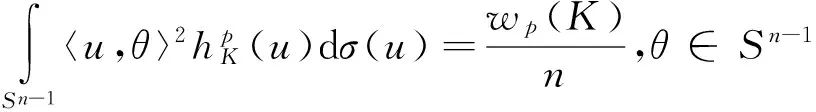
2 最值的存在性