具有变时滞的复值神经网络的有限时间同步

周 超

(重庆师范大学 数学科学学院,重庆 401331)



具有变时滞的复值神经网络的有限时间同步

周 超

(重庆师范大学 数学科学学院,重庆 401331)

研究了具有变时滞的复值神经网络的有限时间同步问题.在一些合理的假设下，基于状态反馈原理和稳定性理论提出了新的控制协议.通过运用新的同步方法得到一些充分条件来保证具有时滞的复值神经网络能在有限时间内同步.

时滞；复值；神经网络；有限时间；同步

近年来，由于神经网络在信号处理、模式识别、最优化问题等各个领域应用非常广泛，因此引起了许多的学者的强烈关注. 而同步作为非常重要的一种现象，也得到了不少学者的青睐，特别是有限时间同步在许多领域中的研究是不可避免的，如信息安全[1]、信息处理[2]等领域. 它不但可以节约达到同步的时间还能在信息传输等应用中提供便利. 控制系统同步的方法很多，如滑模控制[3]、脉冲控制[4]、自适应控制[5]、状态反馈控制[6]等，但得到的结果的保守性各不相同.

在此之前，已经有不少的学者对神经网络同步问题进行了深入地研究[7-11]. 文献[7]对神经网络的指数同步进行了研究，而文献[8-11]通过不同的方法使得系统在有限的时间内同步.特别是文献[11]，提出一种新的方法来获得具有混合时滞的神经网络在有限时间内同步的条件. 然而，在实际应用当中，各类网络往往要比在实数域中研究的网络系统更加复杂．文献[12-15]首先对系统的稳定性进行了分析与探索，且一般运用两种方法来解决复值问题. 而文献[16-17]则开始对系统的同步性进行研究，特别是文献[17]已经对变时滞的复值混沌系统进行研究.本文将通过另一种证明方法及其他的判定方式来解决同类问题.

1 基本定义与预备知识

考虑如下具有变时滞的复值神经网络：

(1)

其中:k=1,2,…,n，n代表神经元的个数，zk(t)∈X表示第k个神经网络在时间t时刻的状态，f(z(t))=(f1(z1(t)),f2(z2(t)),…,fn(zn(t)))T∈Xn,是连续的非线性激励函数，J(t)=(J1(t),J2(t),…,Jn(t))T∈Xn表示外部输入量，D=diag(d1,d2,…,dn)∈Rn×n且dk>0,A=(akj)n×n∈Xn×n,B=(bkj)n×n∈Xn×n,表示连接权重矩阵,τ表示时滞，φ(s)=(φ1(s),φ2(s),…,φn(s))T代表初值.

根据驱动系统(1)，相应的响应系统可以考虑如下：

(2)

其中：u(t)=(u1(t),u2(t),…,un(t))T∈Xn是响应系统在时间t的状态，U(t)=(U1(t),U2(t),…,Un(t))T表示控制输出.

在神经网络的同步中，常常把式(1)和式(2)的同步问题转化为对式(3)的稳定性问题进行探讨. 根据ek(t)=uk(t)-zk(t)可由式(1)和式(2) 得到误差系统的微分方程如下：

(3)

由于状态变量均为复数，则误差也为复数，若ek(t)=xk(t)+iyk(t), 则式(3)可以分成如下两个部分：

(4)

(5)

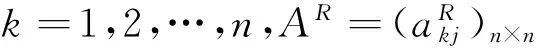
为了设计出合适的控制器使得系统在有限时间内达到同步，在得到结果之前，先给出以下假设和引理.

(H1)fk(·)满足以下条件：

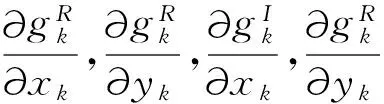
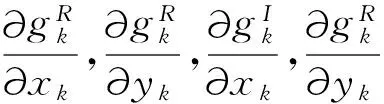
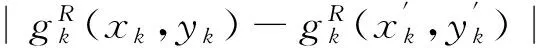
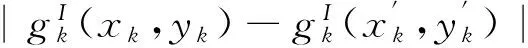
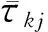
在研究系统的有限时间同步问题时，也可将问题转化为如下描述：

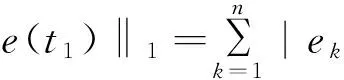
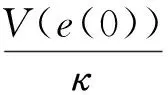
2 主要结论

根据定义1，控制器应当满足当ek(t)=0,k=1,2,…,n时，Uk(t)=0.因此，设计控制器如下：

Uk(t)=-ξkek(t)-δksgn(Rek(t))-iχksgn(Iek(t))

其中Rek(t),Iek(t)代表ek(t)的实部和虚部.由ek(t)=xk(t)+iyk(t)可得：

Uk(t) =-ξk(xk(t)+yk(t))-δksgn(xk(t))-iχksgn(yk(t))=

-ξkxk(t)-δksgn(xk(t))+i(-ξkyk(t)-χksgn(yk(t)))

(6)

于是有：

(7)

(8)

其中：k=1,2,…,n,ξk>0是控制增益，δk>0,χk>0是可调常数.

定义如下变量：

x=(x1,x2,…,xn)T,y=(y1,y2,…,yn)T,α=(xT,yT)T,ω=((UR)T,(UI)T)T,

GR(α)=((gR(x,y))T,(gR(x,y))T)T,GI(α)=((gI(x,y))T,(gI(x,y))T)T.

定义系统(4)和(5)的关系为：

α(t)=-D1α+Q1GR(α)+Q2GI(α)+ω

(9)

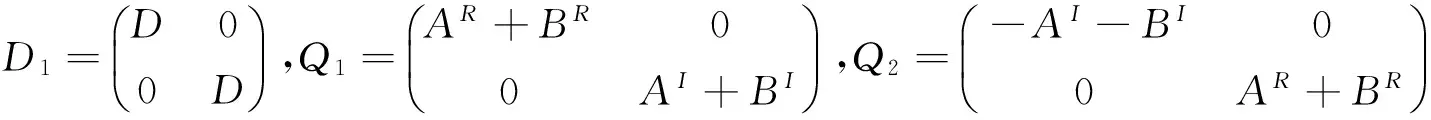
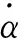
定理1 假设条件H1～H2成立，若控制器(6)中κ=min{δk,χk,k=1,2,…,n}>0，且满足下列条件：

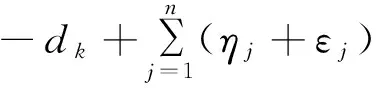
(10)

(11)

其中：

则系统(2)与系统(1)有限时间同步，同步时间估计为：

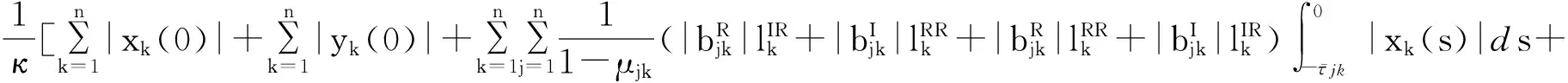
证明：构造Lyapunov-Krasovskii泛函如下：

V(α(t))=V1(α(t))+V2(α(t))

(12)

其中：

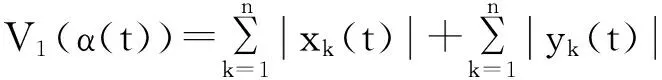
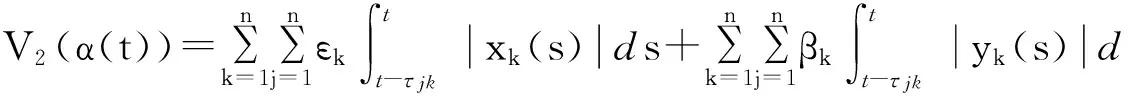
将控制器(7)和(8)分别代入误差系统(4)和(5)， 计算V1(t)沿着轨迹(4)和(5)对时间的导数，根据假设条件H1可得到以下不等式：

ξkxk(t)-δksgn(xk(t))]}+

ξkyk(t)-χksgn(yk(t))]}≤

(13)

根据假设条件(H2)，V2(α(t))关于时间t的导数满足下列不等式：

(14)

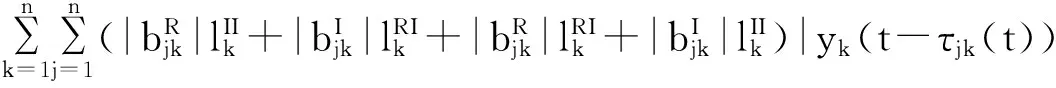
将式(13)和式(14)代入式(12)可得：

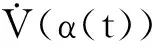
(15)

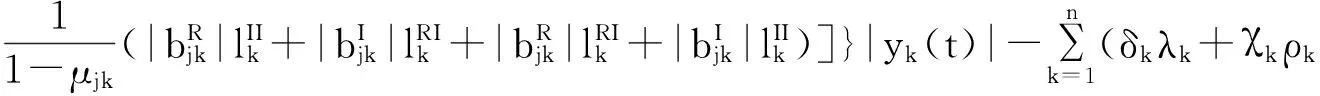
根据定理1的条件，将式(10)及式(11)代入式(15)可得：

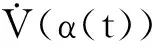
其中：κk=min{δk,χk}>0，当|α(t)| ≠0时，λk+ρk≥1，否则λk+ρk=0.

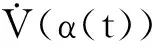
根据引理1可得误差系统(9)在有限时间内稳定，即误差系统(3)在有限时间内可以达到稳定状态.因此，系统(1)和(2)能在有限时间内达到同步，且同步时间估计为：

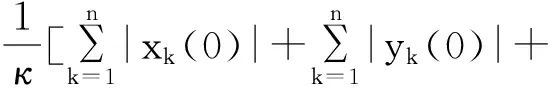
由于本文研究的系统(1)和(2)中具有变时滞，因此，对于常时滞和无时滞的情况，定理1仍然适用.于是根据定理1同样地证明过程可以得到以下推论：

推论1 假设条件(H1)～(H2)成立，若控制器(6)中δk>0,χk>0,k=1,2,…,n,且满足下列条件：

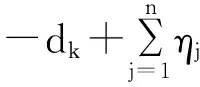
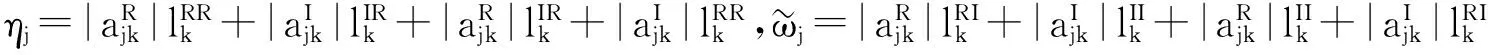
则系统(4)与系统(1)有限时间同步，且同步时间估计为：

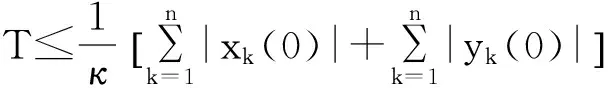
[1] YANG X,YANG Z,NIE X.Exponential synchronization of discontinuous chaotic systems via delayed impulsive control and its application to secure communication[J]. Communications in Nonlinear Science & Numerical Simulation, 2014, 19(5):1529-1543.

[2] XIE Q,CHEN G,BOLLT E.Hybrid chaos synchronization and its application in information processing[J].Mathematical & Computer Modelling, 2002, 35(1):145-163.

[3] ZHANG Q.Robust synchronization of FitzHugh-Nagumo network with parameter disturbances by sliding mode control[J].Chaos Solitons & Fractals,2014,58(1):22-26.

[4] STAMOVA I M,ILARIONOV R,VANEVA R.Impulsive control for a class of neural networks with bounded and unbounded delays[J].Applied Mathematics & Computation,2010,216(1):285-290.

[5] HE W,CAO J,Adaptive synchronization of a class of chaotic neural networks with known or unknown parameters[J].Physics Letters A,2008,372(4):408-416.

[6] PARK J H.Synchronization of cellular neural networks of neutral type via dynamic feedback controller[J].Chaos Solitons & Fractals,2009,42(3):1299-1304.

[7] JUNG C,CHENG.Exponential synchronization of a class of neural networks with time-varying delays[J].Systems Man & Cybernetics Part B Cybernetics IEEE Transactions on,2006,36(1):209-215.

[8] HE P,MA S,FAN T.Finite-time mixed outer synchronization of complex networks with coupling time-varying delay[J].Chaos An Interdisciplinary Journal of Nonlinear Science,2012,22(4):517-525.

[9] HUANG J,LI C,HUANG T,et al.Finite-time lag synchronization of delayed neural networks[J].Neurocomputing,2014,139(13):145-149.

[10] HU C,YU J,JIANG H.Finite-time synchronization of delayed neural networks with Cohen-Grossberg type based on delayed feedback control[J].Neurocomputing,2014,143(16):90-96.

[11] YANG X.Can neural networks with arbitrary delays be finite-timely synchronized?[J].Neurocomputing,2014,143(16):275-281.

[12] ZHANG Z,LIN C,CHEN B.Global Stability Criterion for Delayed Complex-Valued Recurrent Neural Networks[J].Neural Networks & Learning Systems IEEE Transactions on,2014,25(9):1704-1708.

[13] FANG T,SUN J.Stability of complex-valued recurrent neural networks with time-delays[J].Neural Networks and Learning Systems,IEEE Transactions on,2014,25(9):1709-1713.

[14] HU J,WANG J.Global stability of complex-valued recurrent neural networks with time-delays[J].Neural Networks and Learning Systems,IEEE Transactions on,2012,23(6):853-865.

[15] XU X,ZHANG J,SHI J.Exponential stability of complex-valued neural networks with mixed delays[J].Neurocomputing,2014,128(5):483-490.

[16] WU Z,CHEN G,FU X.Synchronization of a network coupled with complex-variable chaotic systems[J].Chaos: An Interdisciplinary Journal of Nonlinear Science,2012,22(2):023127.

[17] WU Z,YE Q,LIU D.Finite-time synchronization of dynamical networks coupled with complex-variable chaotic systems[J].International Journal of Modern Physics C,2013,24(9):2731-2744.

责任编辑：时 凌

Finite-time Synchronization of Complex-valued Neural Networks with Time-varying Delays

ZHOU Chao

(School of Mathematical Sciences, Chongqing Normal University, Chongqing 401331, China)

This paper mainly studies the issues of finite-time synchronization for complex-valued neural networks with time-varying delays. Based on some reasonable assumptions, state feedback theory and stability theory, a new control protocol is proposed.By using a new synchronized method, some sufficient conditions are derived to ensure that the complex-valued neural networks with time-varying delays can realize synchronization in finite time.

delays; complex-valued; neural networks; finite time; synchronization

2016-12-23.

国家自然科学基金项目(61263020)

周超(1988-),男,硕士生,主要从事应用数学的研究.

1008-8423(2017)02-0125-06

10.13501/j.cnki.42-1569/n.2017.06.002

O29

A